PSD29007-Engtelecom(2020-1) - Prof. Marcos Moecke
1 Registro on-line das aulas
1.1 Unidade 1
| Unidade 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
profile on
profile viewer Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz).
|
1.2 Unidade 2
| Unidade 2 - Filtros IIR | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Na sequência será mostrado como inicialmente projetar o filtro LP protótipo, e depois as transformações em frequência.
%%Definição do filtro
% Definindo os coeficientes do filtro
b = [1 1]; % Numerador
a = [1 1 5]; % Denominador
% Calculando os zeros (raízes do numerador) e pólos (raízes do denominador)
% Método 1 - usando a função tf2zp
[z1,p1,k]=tf2zp(b,a)
% Método 2 - obtendo as raízes
z2 = roots(b);
p2 = roots(a);
zplane(b,a);
%% Obtendo a resposta em frequência
% substitituindo a variável complexa s por jw usando a função freqz
freqs(b,a);
% Usando cálculo simbólico e plotando o gráfico com semilogx
syms s w
H(s) = (s+1)/(s^2 + s + 5);
pretty(H(1j*w))
latex(H(1j*w))
%%
ws = logspace(-2, 1, 1000);
h = H(1j*ws);
subplot(211)
plot(ws,abs(h)); grid on;
%semilogx(ws,abs(h)); grid on;
subplot(212)
plot(ws,angle(h)/pi*180); grid on;
%semilogx(ws,angle(h)/pi*180); grid on;
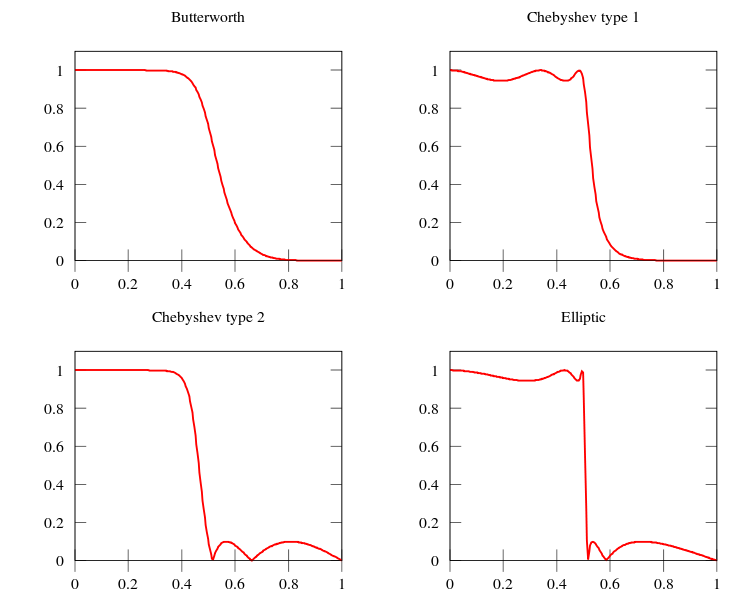
Os projetos de filtro Butterworth com função de transferência utilizam os polinômios de Butterworth mostrados na tabela a seguir:
1.2.1 INÌCIO DAS AULAS REMOTAS
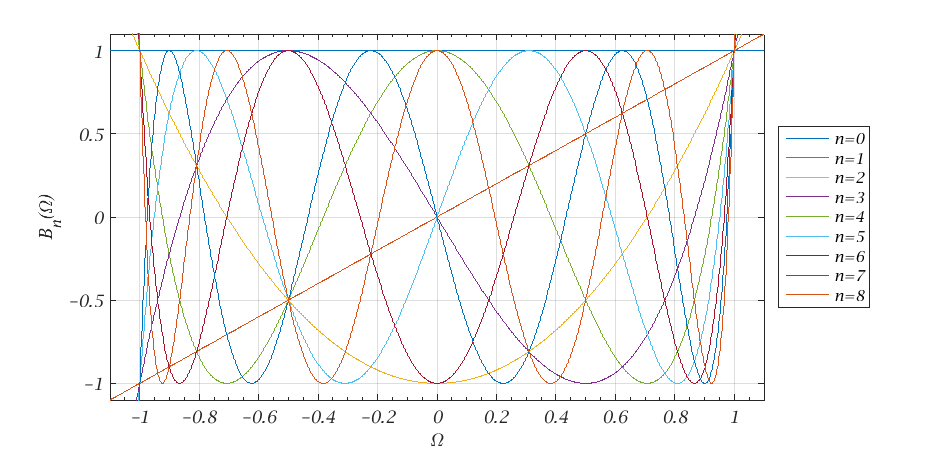
Para o projeto dos filtros do tipo Chebyshev, são utilizados os polinômios de Chebyshev de primeira ordem, os quais são definidos pela equação trigonométrica: Os dois primeiros polinômios são facilmente calculados como: O cálculo dos demais termos pode ser feita pela relação recursiva: Portanto o polinômio de grau 2 pode ser obtido por Assim os primeiros nove polinômios de Chebyshev de primeira ordem podem ser obtidos: Esses polinômios mostram um comportamento oscilatório entre . FONTE: Polinômios de Tchebychev, Wikipedia
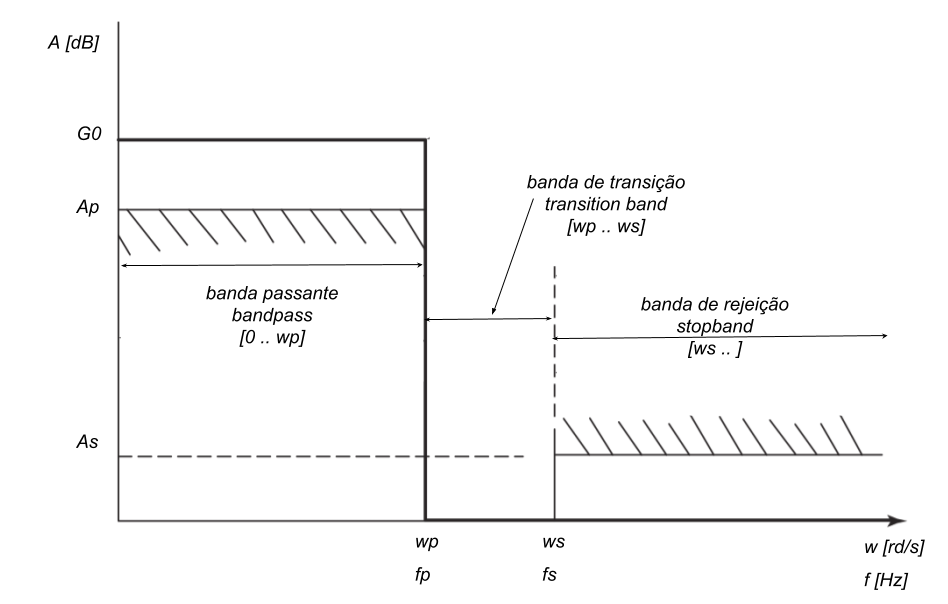
Para o projeto de filtros analógicos é necessário fazer as transformações de frequência indicadas abaixo, as quais devem ser consideradas no momento da determinação dos parâmetros do filtro protótipo LP.
%% Projeto de filtro passa-alta (HP) usando funções do Matlab
Wp = 150; % rad/s
Ws = 40; % rad/s
Rp = 3; % dB
Rs = 60; % dB
[n,Wn] = buttord(Wp,Ws,Rp,Rs,'s')
[b,a] = butter(n,Wn,'high','s');
[h,w] = freqs(b,a,logspace(1,3,1000));
semilogx(w,20*log10(abs(h)));grid on;
hold on; plot([Wp Wn Ws],[-Rp -3 -Rs],'x'); hold off;
title(sprintf('Filtro HP Butterworth, n = %d',n))
%% Projeto de filtro passa-faixa (BP) usando funções do Matlab
Wp = [100 200]; % rad/s
Ws = [50 250]; % rad/s
Rp = 3; % dB
Rs = 40; % dB
[n,Wn] = buttord(Wp,Ws,Rp,Rs,'s');
[b,a] = butter(n,Wn,'s');
freqs(b,a,logspace(1,3,1000))
title(sprintf('Filtro BP Butterworth, n = %d',n))
%% Projeto de filtro passa-baixas usando funções do Matlab
%% Especificações do filtro
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');
%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');
%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');
%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');
fa = 200;
fN = fa/2;
wo = 60/fN; bw = 10/fN;
[b,a] = iirnotch(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000;
fN = fa/2;
wo = 941/fN; bw = 100/fN;
[b,a] = iirpeak(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000; fN = fa/2;
fo = 1000; bw = 20/fN;
[b,a] = iircomb(fa/fo,bw,'peak'); % ou use a flag 'notch'
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
|
- Dias 4, 7, 11 e 14 mai
- Parada Pedagógica sem aulas de acordo com a resolução do colegiado do campus de São José.
- Dia 18 mai
- Retorno às ANPs, porém sem aula de acordo com mensagem recebida do chefe do DEPE.
- Foi solicitado que todos alunos se cadastram no workspace da disciplina no SLACK.
- Foi solicitado que todos alunos respondam a uma sondagem sobre as ANPs Volta às aulas não presenciais em tempo de pandemia.
- Resultado das outras enquetes:
- Você gostaria que a UC de PSD29007 tivesse continuidade através de ANPs durante a pandemia do corona virus?
- sim
- █████████████████████████ | 100% (11)
- não
- A que horas começar as aulas?
- 7:30
- ████████ | 33% (3)
- 7:45
- ██████████████ | 56% (5)
- 8:00
- ██ | 11% (1)
- 8:15
- | 0% (0)
1.3 Unidade 3
| Unidade 3 - Filtros FIR | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
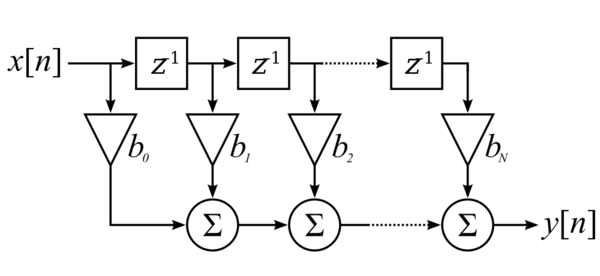 A determinação da resposta ao impulso do filtro pode ser feita substituindo a entrada por . O resultado é , e portanto a resposta ao impulso tem duração igual ao número de coeficientes N+1 (onde N é a ordem do filtro). Esse é o motivo pelo qual o filtro tem o nome de filtro de resposta ao impulso finita (FIR - Finite Impulse Response). O filtro também recebe nomes como filtro transversal, Filtro não recursivo, filtro de média móvel, e tapped delay filter (torneira com atrasos?). A função de transferência também pode ser descrita como: Algumas vantagens que os filtros FIR tem sobre os IIR: 1. É possível projetar FIR com fase linear, ou seja atraso de grupo constante. Esses filtros são desejáveis na transmissão de sinais digitais.
2. As amostras da resposta ao impulso são os coeficientes do filtros , e portanto não precisam ser calculadas. 3. Os FIR são sempre estáveis pois tem todos os polos na origem. Também é consequência de não ter realimentação. Por isso também não tem ciclo limite que surge nos filtros IIR como resultado da resposta ao impulso de duração infinita associada a representação dos coeficientes e dos sinais com palavras de comprimento finito de bits. 4. O efeito da representação dos coeficientes e dos sinais com palavras de comprimento finito de bits, na resposta de frequência e resposta no domínio do tempo é menor que nos IIR.
Os filtros de fase linear possuem algumas propriedades (respostas em frequência possíveis, distribuição dos zeros em simetria quadrantal), conforme é mostrado a seguir.
N = 10;
bi = 2*(rand(1,N)-0.5)
%% Tipo I - LP, HP, BS, BP
b = [bi (2*rand(1,1)-0.5) flip(bi)];
fvtool(b,1);
%% Tipo II - LP, BP
% tem um zero em -1
b = [bi flip(bi)];
fvtool(b,1);
%% Tipo III - BP
% tem um zero em 1 e -1
b = [bi 0 -flip(bi)];
fvtool(b,1);
%% Tipo IV - BP, HP
% tem um zero em 1
b = [bi -flip(bi)];
fvtool(b,1);
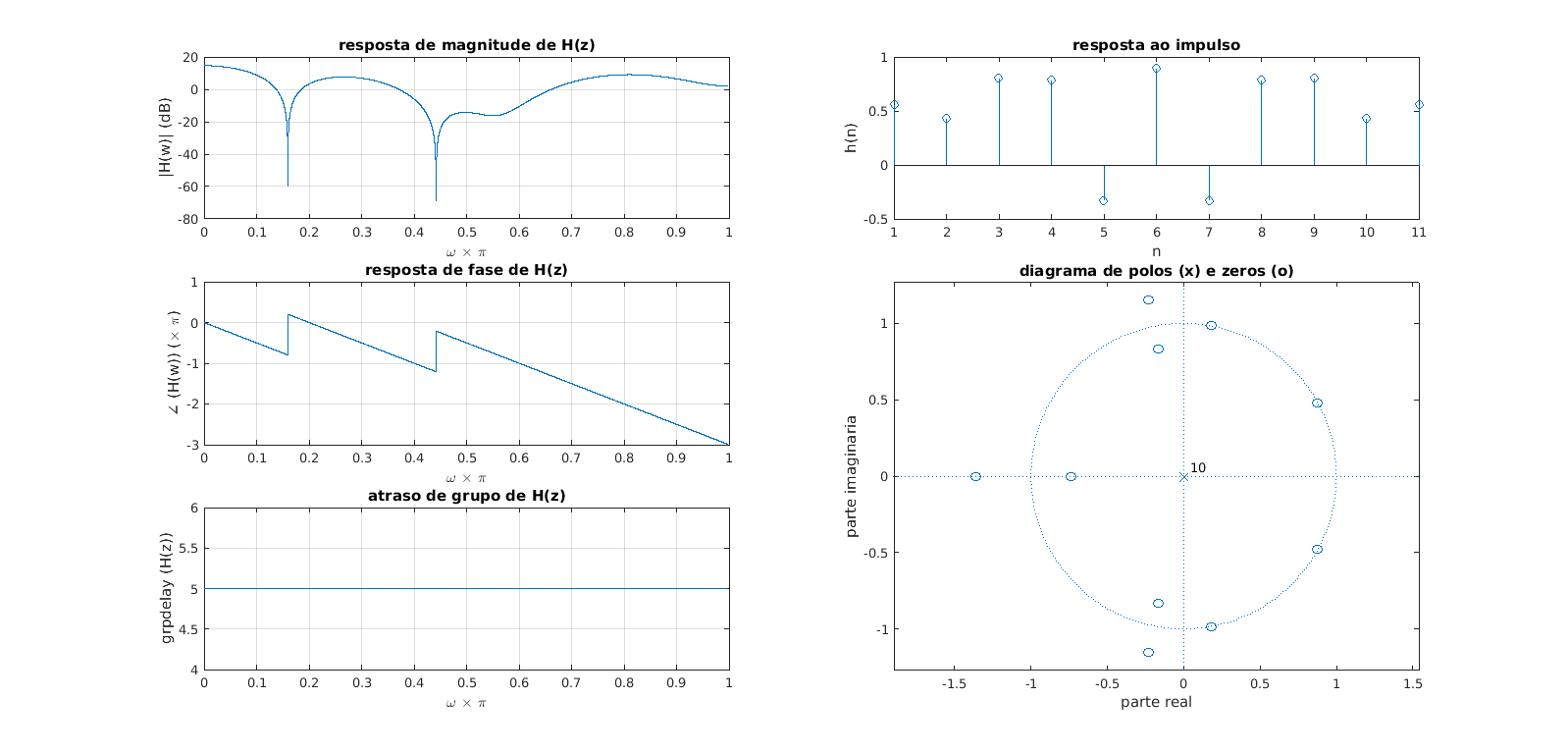
1.3.1 FIR tipo IConsidere o exemplo de um filtro simétrico de ordem par (N=6) Se ele apresenta simetria dos coeficientes , e , temos que: Para obter a resposta em frequência , substituímos . Aplicando a identidade , obtemos que: Portanto a resposta em frequência tem um resposta de magnitude com uma parte real , e uma fase linear igual a , e portanto o atraso de grupo é , que é a metade da ordem N do filtro. Pode-se generalizar este resultado para qualquer filtro simétrico de ordem par: Na qual se percebe que a fase linear é igual a , e portanto o atraso de grupo é , metade da ordem N do filtro. 1.3.2 FIR tipo IIConsidere o exemplo de um filtro simétrico de ordem impar (N=5) Se ele apresenta simetria dos coeficientes , e , temos que: Para obter a resposta em frequência: Aplicando a identidade , obtemos que: Portanto a resposta em frequência tem um resposta de magnitude com uma parte real , e uma fase linear igual a , e portanto o atraso de grupo é , que é a metade da ordem N do filtro. Pode-se generalizar este resultado para qualquer filtro simétrico de ordem impar: Na qual se percebe que a fase linear é igual a , e portanto o atraso de grupo é , metade da ordem N do filtro. 1.3.3 FIR tipo IIIConsidere o exemplo de um filtro antissimétrico de ordem par (N=6) Se ele apresenta simetria dos coeficientes , , e , temos que: Para obter a resposta em frequência , substituímos . Aplicando a identidade , e que obtemos que: Portanto a resposta em frequência tem um resposta de magnitude com uma parte real , e uma fase linear igual a , e portanto o atraso de grupo é , que é a metade da ordem N do filtro. Pode-se generalizar este resultado para qualquer filtro antissimétrico de ordem par: Na qual se percebe que a fase linear é igual a , e portanto o atraso de grupo é , metade da ordem N do filtro. 1.3.4 FIR tipo IVConsidere o exemplo de um filtro antissimétrico de ordem impar (N=5) Se ele apresenta simetria dos coeficientes , e , temos que: Para obter a resposta em frequência: E portanto Portanto a resposta em frequência tem um resposta de magnitude com uma parte real , e uma fase linear igual a , e portanto o atraso de grupo é , que é a metade da ordem N do filtro. Pode-se generalizar este resultado para qualquer filtro antissimétrico de ordem impar: Na qual se percebe que a fase linear é igual a , e portanto o atraso de grupo é , metade da ordem N do filtro. 1.3.5 Propriedades dos filtros FIR de fase linearComo mostrado acima, os filtros que exibem simetria ou antissimetria em seus coeficientes (ou resposta ao impulso), apresentam fase linear (ou atraso de grupo constante). Também foi mostrado que o atraso de grupo é igual a N/2 onde N é a ordem do filtro. Foi demonstrado por Rabiner *** que apenas esses quatro tipos de filtro FIR possuem essa característica, portanto pode-se afirma que "Se e somente se o filtro FIR possui coeficientes simétrico ou antisimétricos ele possui fase linear". Em relação a posição dos zeros, é possível verificar que cada zero sobre o circulo unitário produz uma resposta de magnitude nula na frequencia angular correspondente e um salto de fase de . N = 5;
bi = 2*(rand(1,N)-0.5)
b = [bi (2*rand(1,1)-0.5) flip(bi)];
[h,w] = freqz(b,1,'whole');
figure(1);
subplot(421);
plot(w/pi,20*log10(abs(h))); grid on;
xlabel('\omega / \pi'); ylabel ('magnitude - dB');
subplot(423);
plot(w/pi,angle(h)/pi); grid on;
xlabel('\omega / \pi'); ylabel ('fase - rad / \pi');
subplot(425);
plot(w/pi,unwrap(angle(h))/pi); grid on;
xlabel('\omega / \pi'); ylabel ('fase - rad / \pi');
subplot(427); grpdelay(b,1);
xlabel('\omega / \pi'); ylabel ('atraso de grupo - amostras');
subplot(4,2,[2,4,6,8]); zplane(b,1);
xlabel('real'); ylabel ('imaginario');
Também devido a existência (ou não) de zeros em e , que corresponde a frequência de Nyquist , mostramos que a resposta de magnitude nessas frequencias é nula (ou não). Assim os tipos 1, 2, 3 e 4 de filtros FIR resultam em:
Essa característica é importante conhecer antecipadamente pois implicará no número de coeficientes e na escolha do tipo de (anti)simetria. Por exemplo para filtro BS apenas o Tipo 1 pode ser usado. Outra propriedade a ser destacada é em relação aos zeros do filtro. Em primeiro vamos analisar a consequencia da simetria nos coeficientes : fazendo na segunda equação N-n = m, temos que os limites n = 0 -> m = N, e n = N -> m = 0. Com a mesma análise para antissimetria nos coeficientes : Nessas duas equações é possível perceber que se é um zero então também será um zero de . No caso de zeros reais, se temos um zero então também é um zero, exceto se ou . Por outro lado, se todos os coeficientes b(n) do filtro são reais, então os zeros complexos, aparecem em pares complexos conjugados e , e seus reciprocos e também são zeros de . Esse tipo de disposição dos zeros denominamos de simetria quadrantal.
FONTE:
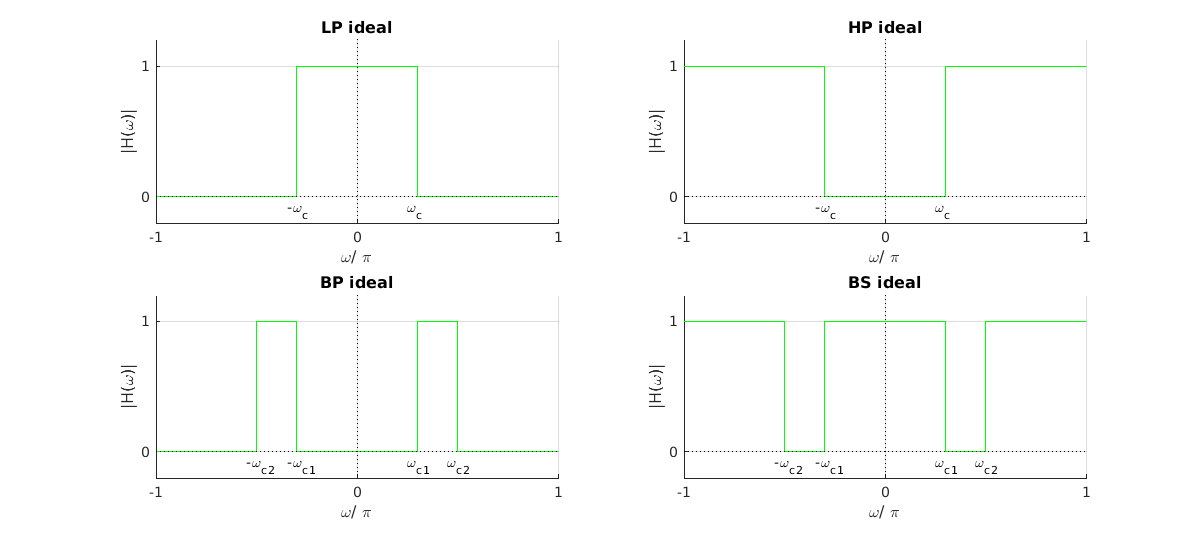
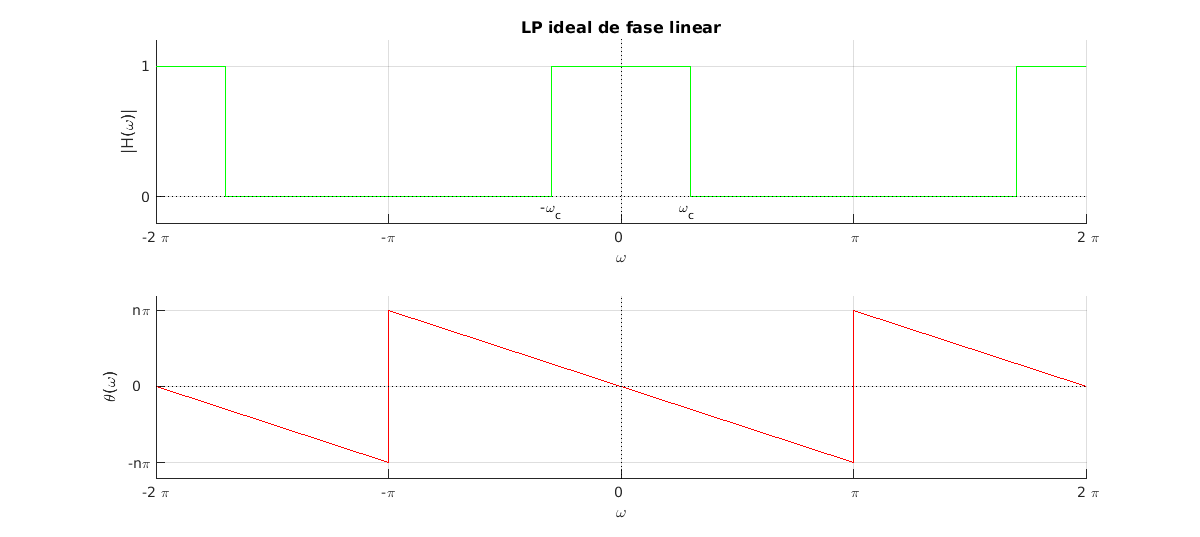
1.3.6 Projeto de filtros FIR pelo método da série de FourierUsando a representação dos filtros ideais LP, HP, BP, BS, com frequências de corte e ganho unitário na banda de passagem e ganho zero na banda de rejeição, e considerando que a magnitude das respostas em frequência é uma função periódica em , e conhecendo as equações de síntese e análise de um sinal (ou sistema) onde É possível coeficientes da série de Fourier de filtros ideais: LP, HP, BP, BS
De modo semelhante é possível obter os coeficientes dos filtros HP, BP e BS.
onde sabe-se que , ou seja para e para .
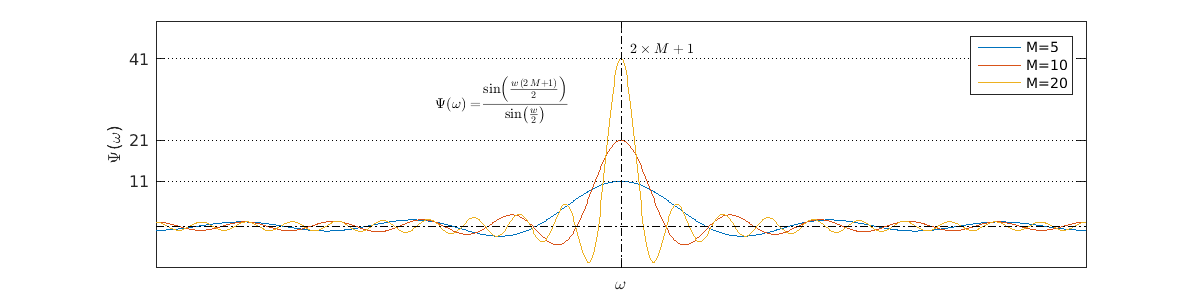
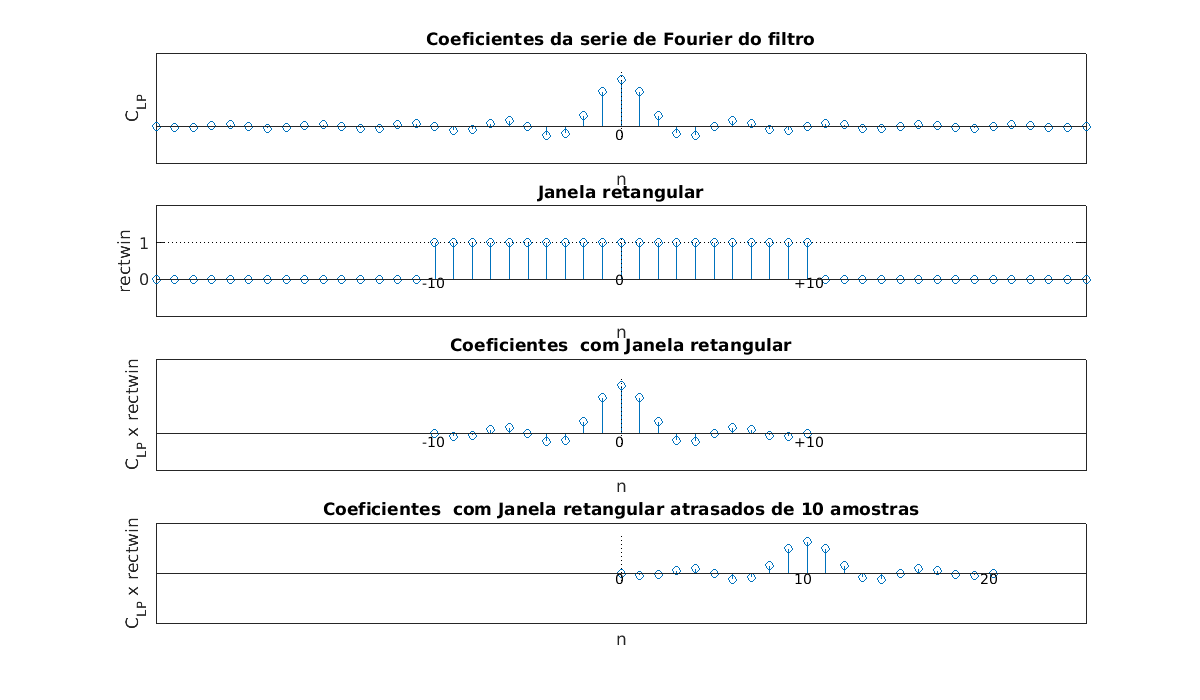
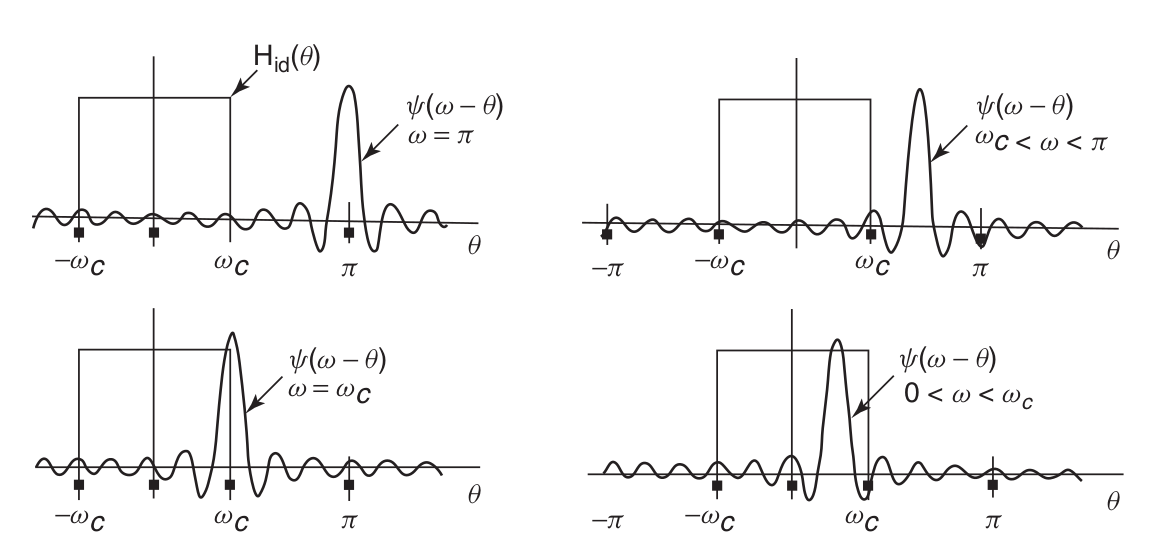
Aplicando a equação de síntese da série obtemos: Note que esta função tem um máximo em , e cruza o zero em , portanto a lagura do lóbulo central é de . Além disso percebe-se que se aumentamos o tamanho da janela retangular (2M+1), a largura do lóbulo central é reduzida proporcionalmente. Ao fazer o "janelamento" dos coeficientes da série de Fourier da resposta em frequência do filtro ideal, estamos multiplicando a série de coeficientes pelo janela retangular , conforme mostra a figura a seguir. Essa multiplicação no domínio do tempo corresponde a uma convolução no domínio da frequência. A qual é mostrada graficamente na figura a seguir.
L = 64;
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));
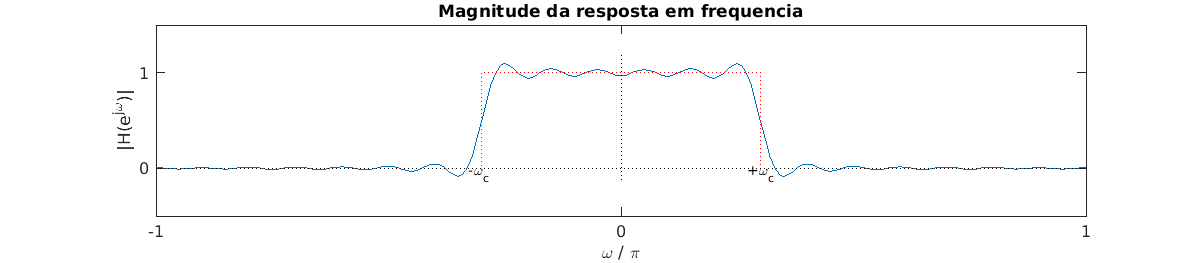
Use o código abaixo e verifique o efeito das diferentes janelas temporais sobre a magnitude da resposta em frequência, sobre a resposta ao impulso, posição dos zeros no plano z, etc.
N = 32;
wc = 0.5; M = N/2;
CLP = wc*sinc(wc*(-M:M));
bRET = CLP;
bHAM = CLP.*hamming(2*M+1)';
bBLACK = CLP.*blackman(2*M+1)';
fvtool(bRET,1,bHAM,1,bBLACK,1);
legend('rectwin', 'Hamming', 'Blackman');
ylim([-0.1 0.1])
wp = 0.2*pi; Ap = 1 dB; Gp = 0 dB ws = 0.4*pi; As = 40 dB;
ws = 0.4*pi; Ap = 0.2 dB; Gp = 0 dB wp = 0.6*pi; As = 50 dB;
L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
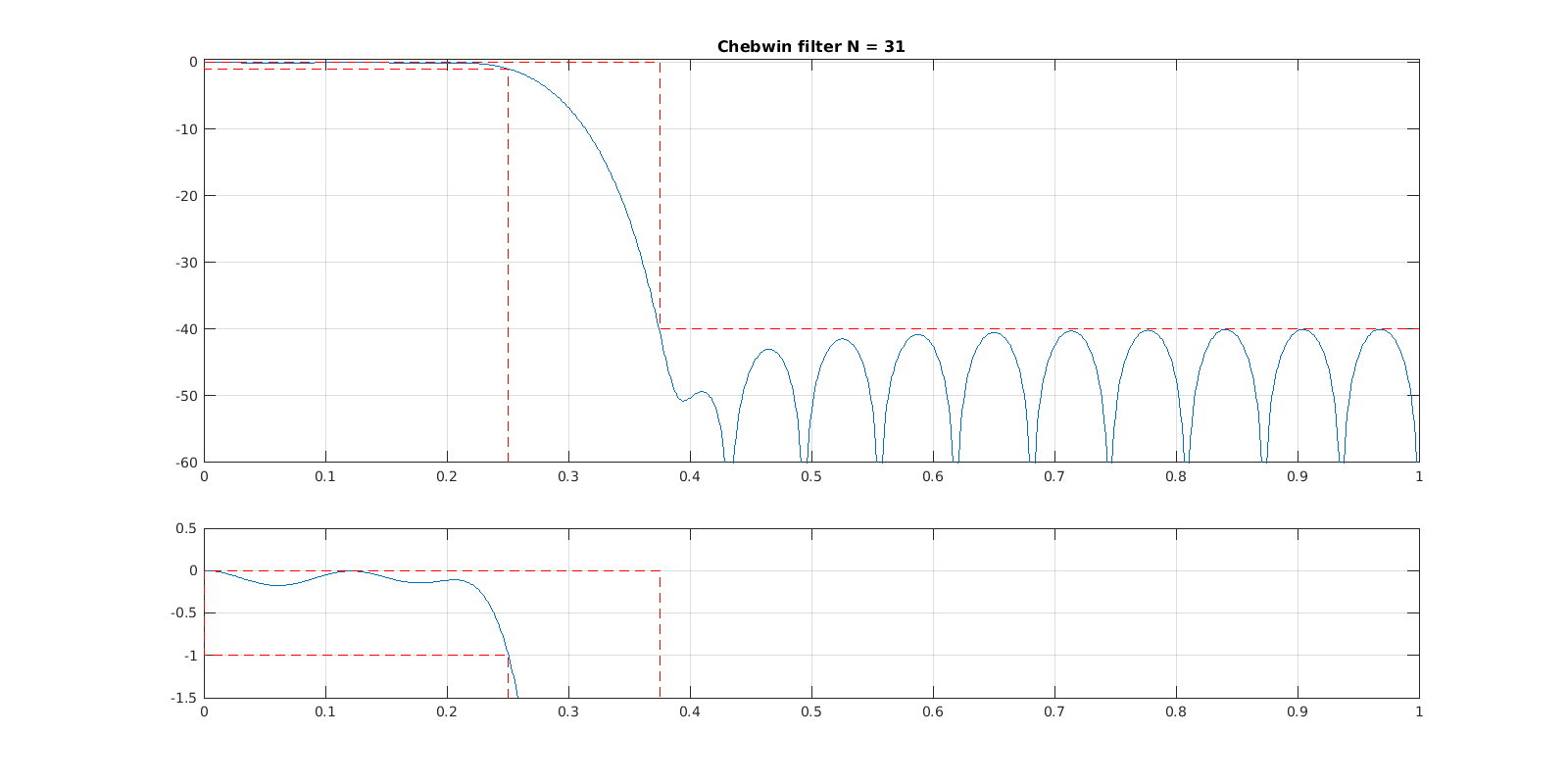
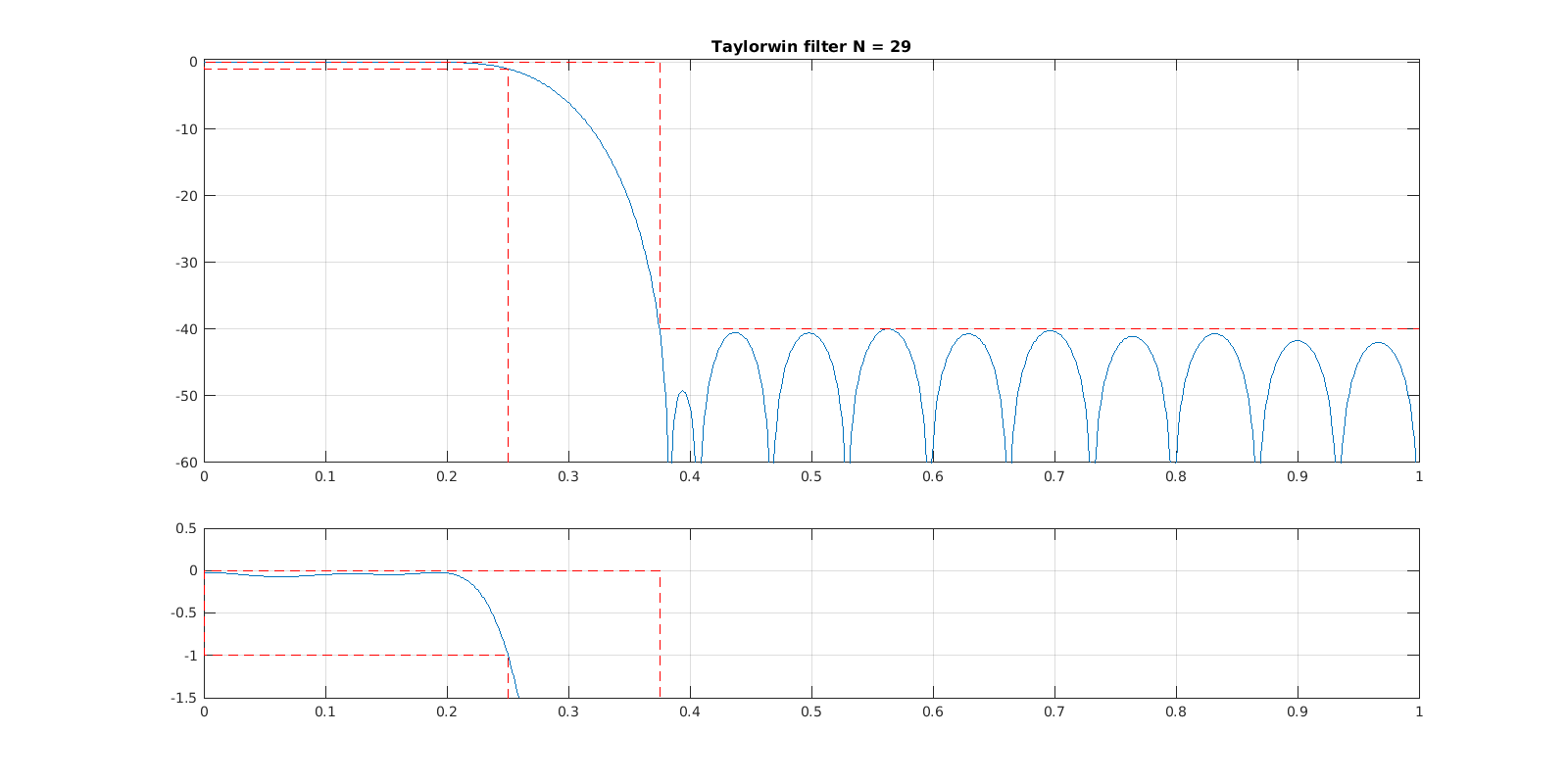
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
Para a janela de Kaiser, a estimação do fator e da ordem do filtro são obtidos por:
onde é a atenuação do lóbulo lateral e é a largura da banda de transição em rad/amostra. A janela de Kaiser é definida por:
onde : é a função de Bessel de ordem zero [2] Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com , , atenuação de 40 dB na "stopband" %% Calculo do filtro de kaiser, sem ajustes
% Especificaçao
fsamp = 8000;
fcuts = [1000 1500];
Ap = 1;
As = 40;
ftype = 'low';
fN = fsamp/2;
wp = fcuts(1)/fN;
ws = fcuts(2)/fN;
Dw = abs(ws-wp);
% Calculo da janela de Kaiser
beta = 0.5842*(As-21)^0.4+0.07886*(As-21);
n = ceil((As-8)/(2.285*Dw*pi)+1);
Wn = (wp+ws)/2;
wkaiser = kaiser(n+1,beta);
Forma alternativa de projeto usando a função kaiserord fsamp = 8000;
fcuts = [1000 1500];
Ap = 1;
As = 40;
mags = [1 0];
devs = [1-10^(-Ap/20) 10^(-As/20)];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
wkaiser = kaiser(n+1,beta);
h_fir = fir1(n,Wn,ftype,wkaiser,'noscale');
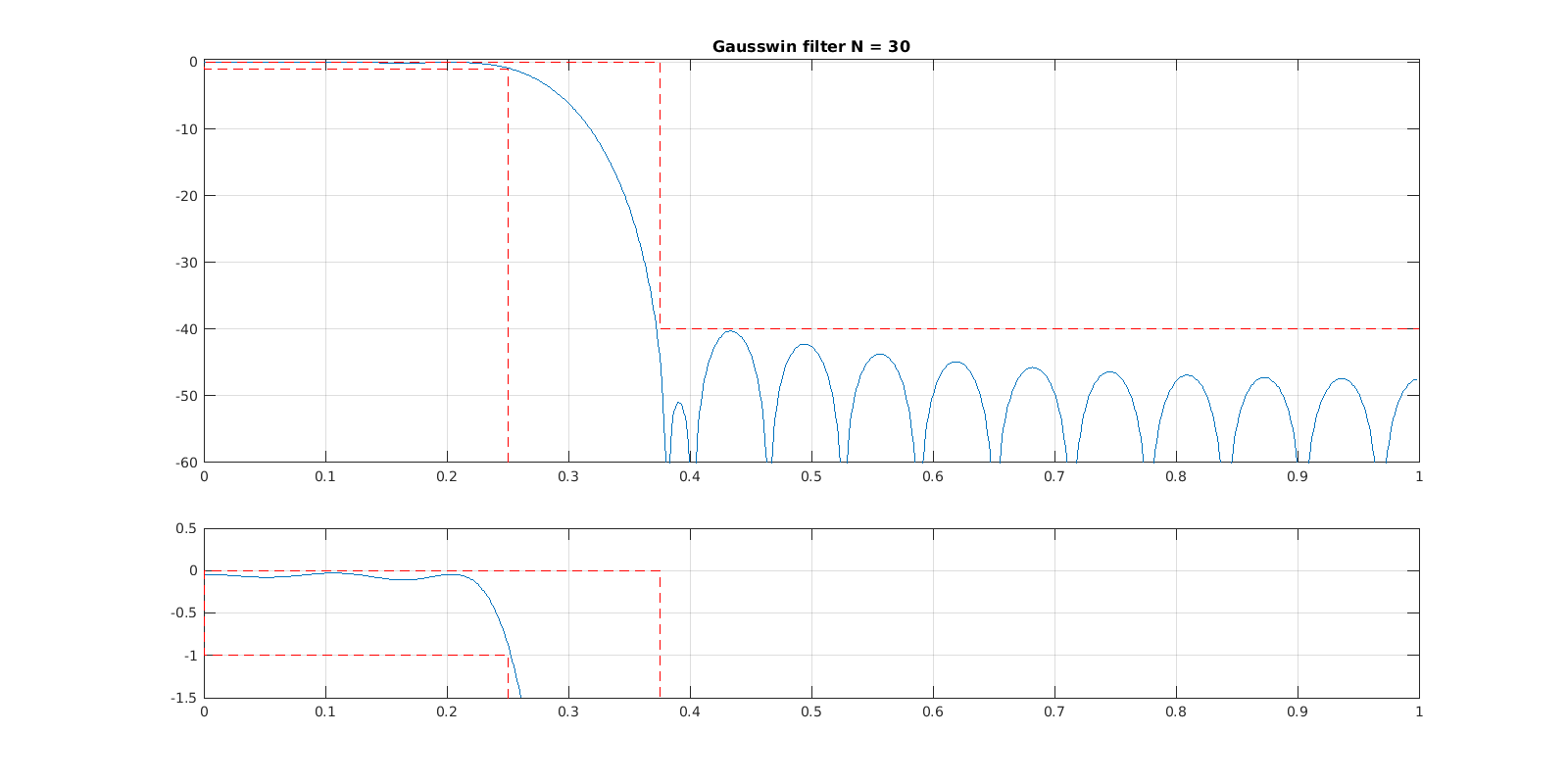
A partir das especificações do filtro é possível obter um projeto usando a função fir1. Essa função basicamente aplica o método da janela ao filtro ideal especificado pela(s) frequência(s) de corte . h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[Hw,w] =freqz(h_fir);
plot(w*fsamp/2/pi,20*log10(abs(Hw)))
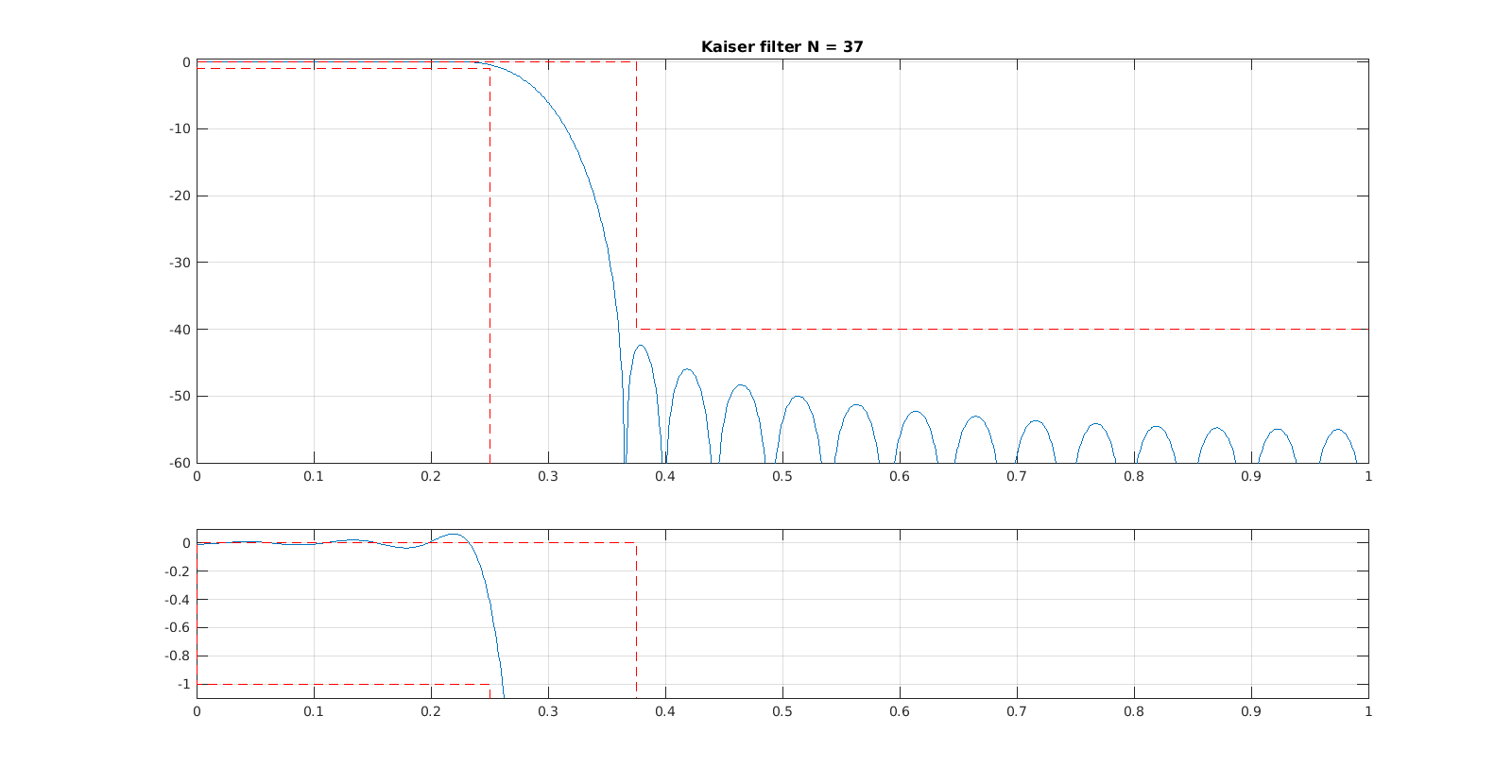
title(['Kaiser filter N = ' num2str(n)])
%fvtool(h_fir,1)
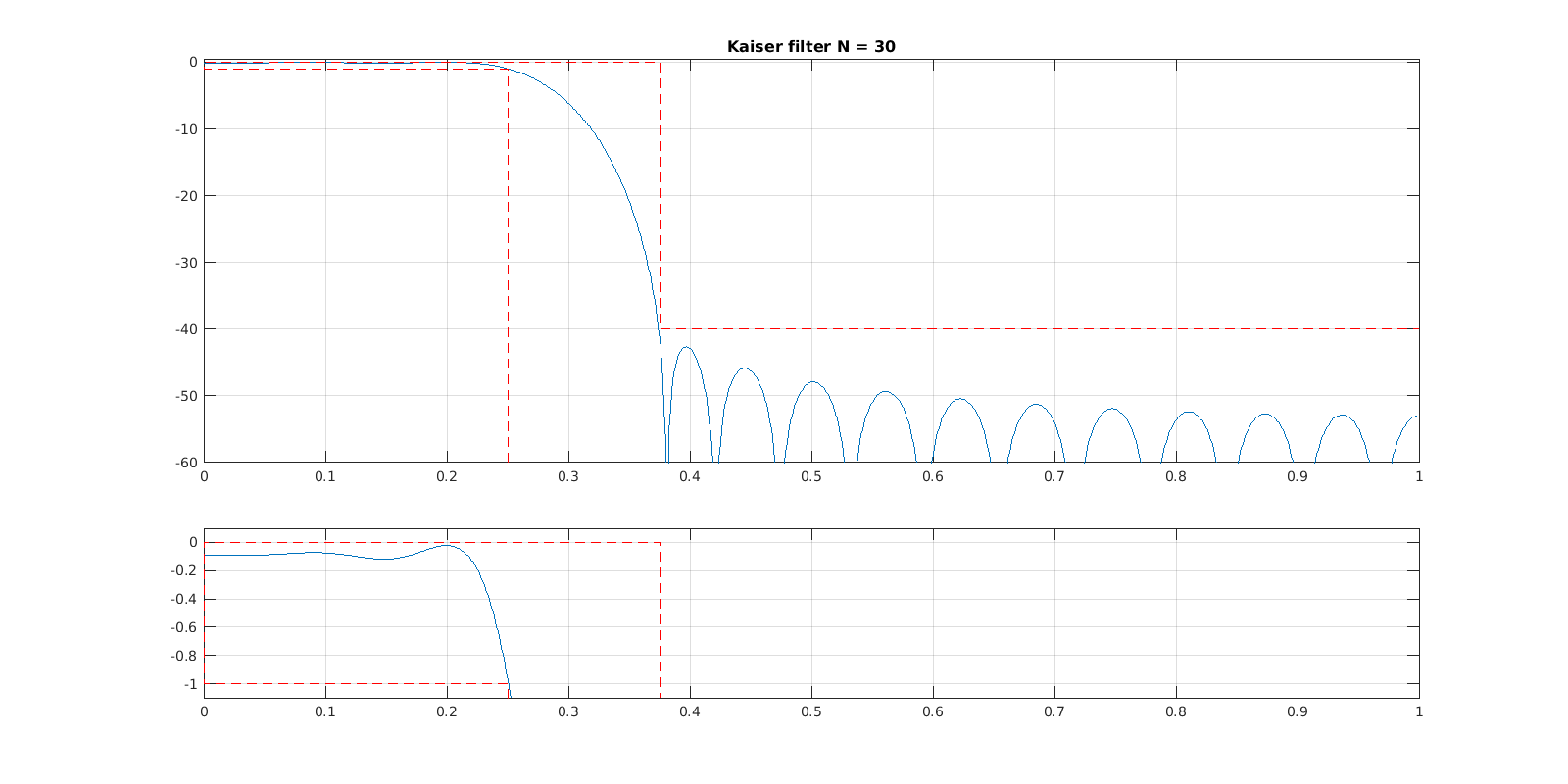
Como resultado do projeto a partir das equações de Kaiser é obtido o filtro abaixo: No entanto realizando ajustes tanto do ganho no topo , na largura da banda de transição , e na ordem do filtro , é possível reduzir essa ordem obtendo o filtro abaixo: L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
Digital Filters with Linear Phase].
fa = 8000;
Ap = 1;
Ar = 40;
fp = 1000;
fr = 1500;
f = [fp fr];
a = [1 0];
dev = [(10^(Ap/20)-1)/(10^(Ap/20)+1) 10^(-Ar/20)];
[n,fo,ao,w] = firpmord(f,a,dev,fa);
b = firpm(n,fo,ao,w);
[h,w] = freqz(b,1,1024,fa);
plot(w, 20*log10(abs(h))); hold on;
plot([0 fr fr fa/2], [Ap/2 Ap/2 -Ar -Ar],':m')
plot([0 fp fp], [-Ap/2 -Ap/2 -(Ar+30)],':m');
ylim([-(Ar+30) Ap/2+10])
|
1.4 Unidade 4 - Realização de Filtros
| Unidade 4 - Realização de Filtros |
|---|
Para exemplificar as diferentes realizações utilizaremos com base um filtro de ordem 4 representado pela função de transferência
Figura 4.1 - Realização de filtros FIR na Forma Direta 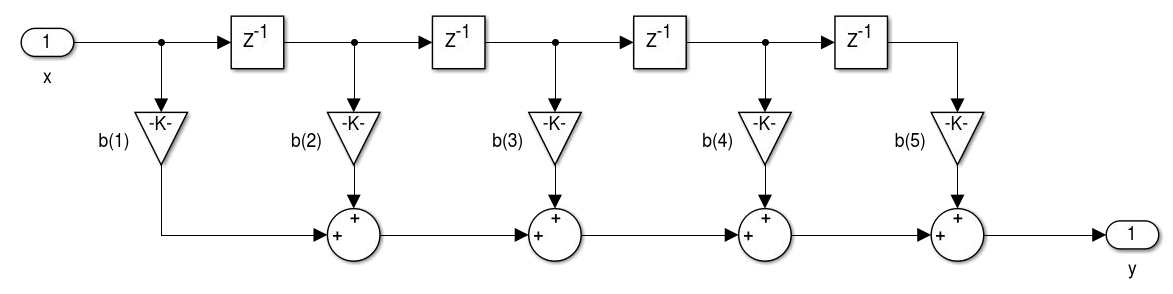
Figura 4.2 - Realização de filtros FIR na Forma Transposta 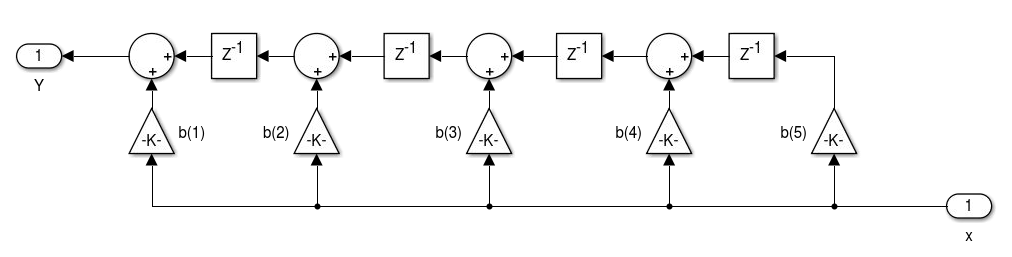 Figura 4.3 - Realização de filtros FIR na Forma Transposta 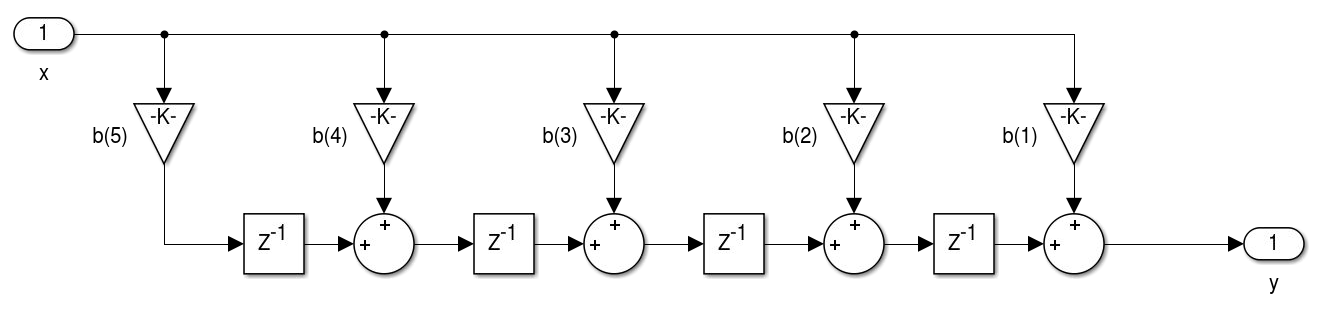
Os filtros FIR de fase linear podem ser com coeficientes simétricos (tipo I e II) ou antissimétricos (tipo III e IV).
Figura 4.4 - Realização de filtros FIR de fase linear Simétrico I 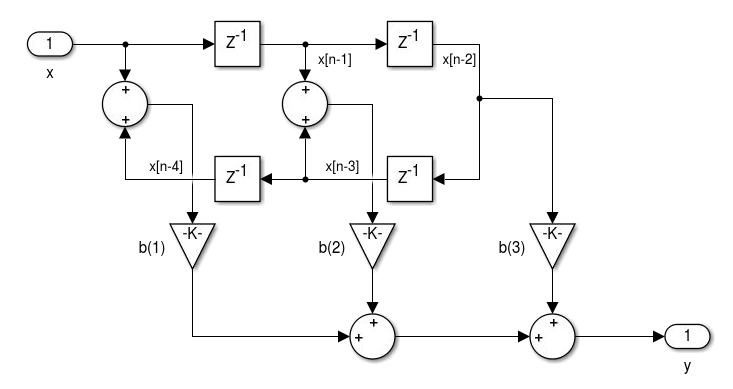
Figura 4.5 - Realização de filtros FIR de fase linear Simétrico II 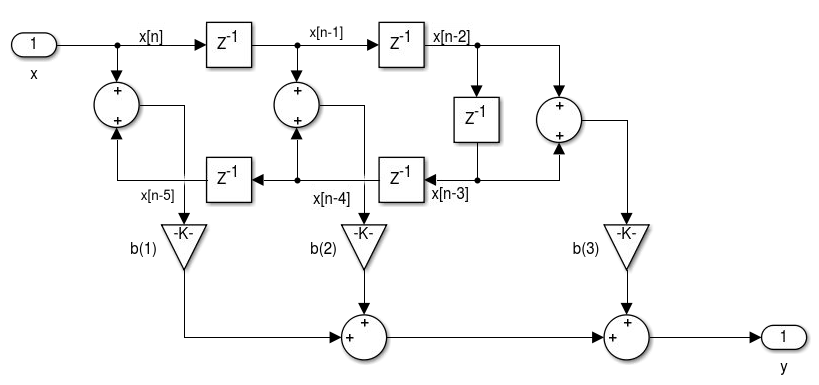
Figura 4.6 - Realização de filtros FIR de fase linear Antisimétrico III 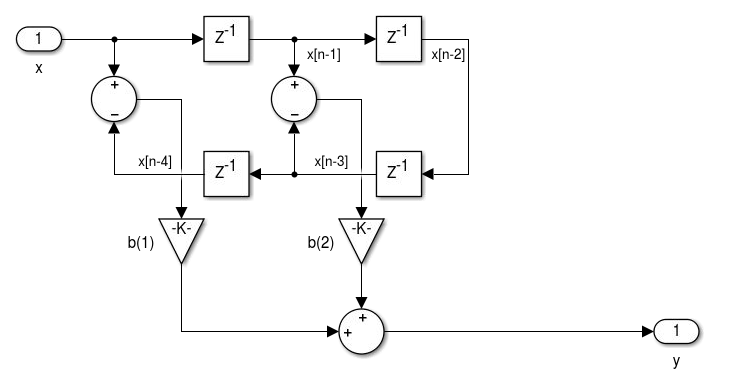
Figura 4.7 - Realização de filtros FIR de fase linear Antisimétrico IV 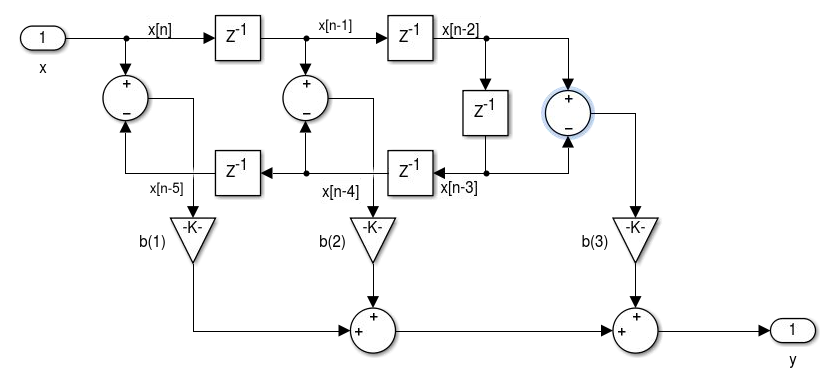
Fs = 30000; % Sampling Frequency
Fpass = 12000; % Passband Frequency
Fstop = 13000; % Stopband Frequency
Dpass = 0.01; % Passband Ripple
Dstop = 0.01; % Stopband Attenuation
flag = 'scale'; % Sampling Flag
% Calculate the order from the parameters using KAISERORD.
[N,Wn,BETA,TYPE] = kaiserord([Fpass Fstop]/(Fs/2), [1 0], [Dstop Dpass]);
% Calculate the coefficients using the FIR1 function.
b = fir1(N, Wn, TYPE, kaiser(N+1, BETA), flag);
hFIR = dsp.FIRFilter;
hFIR.Numerator = b;
% Para definir diretamente os coeficientes
realizemdl(hFIR)
% Para definir os coeficientes através de uma matriz de entrada
realizemdl(hFIR,'MapCoeffsToPorts','on');
Figura 4.8 - Separação do filtro IIR H(z) em H1(z) e H2(z) 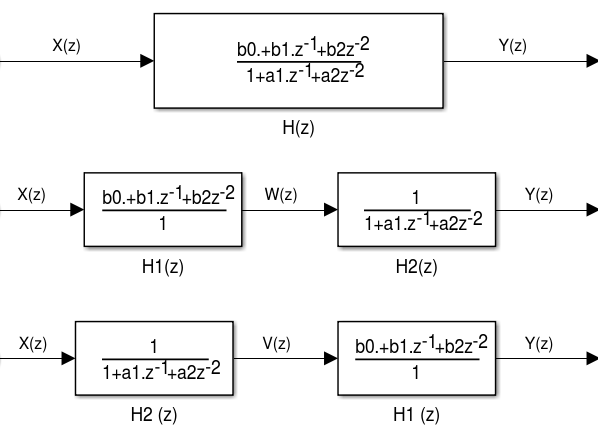
Figura 4.9 - Realização de filtros IIR na Forma Direta I 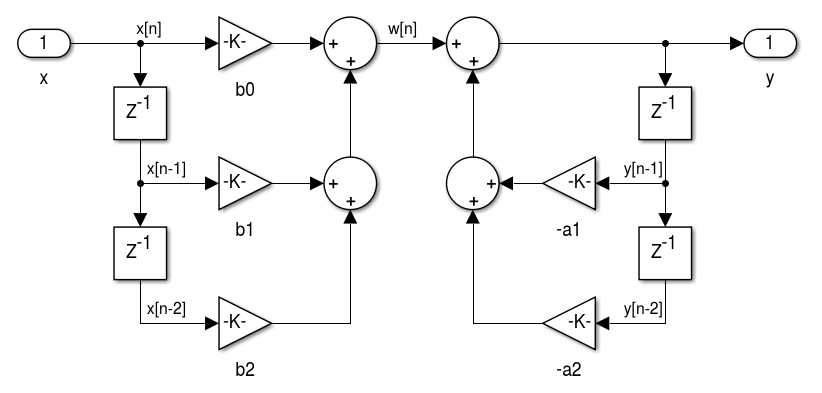
Figura 4.10 - Realização de filtros IIR na Forma Direta II 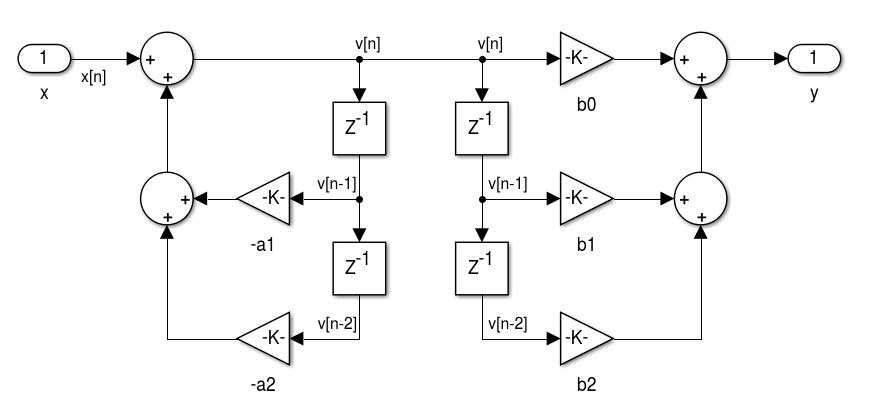
Figura 4.11 - Realização de filtros IIR na Forma Direta II Canônica 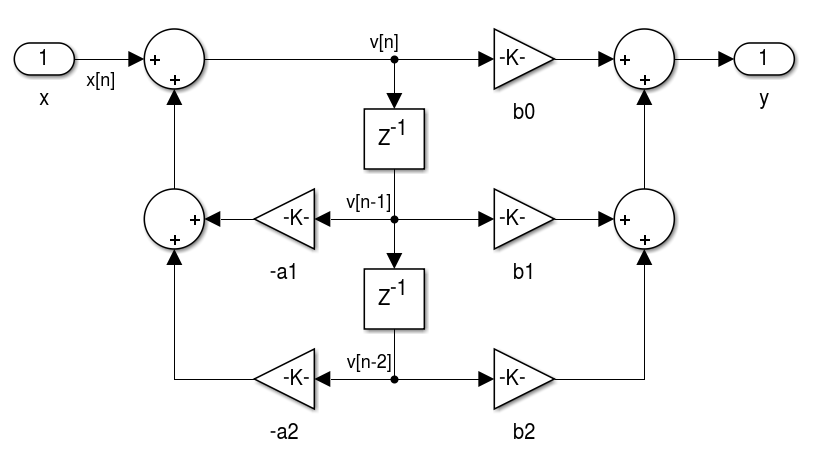
Figura 4.12 - Realização de filtros IIR na Forma Transposta I 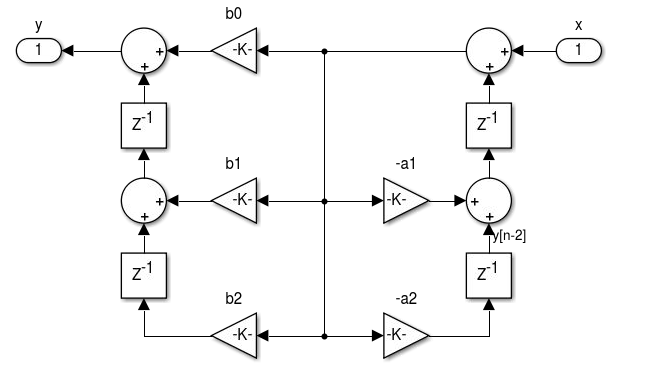 Figura 4.13 - Realização de filtros IIR na Forma Transposta II 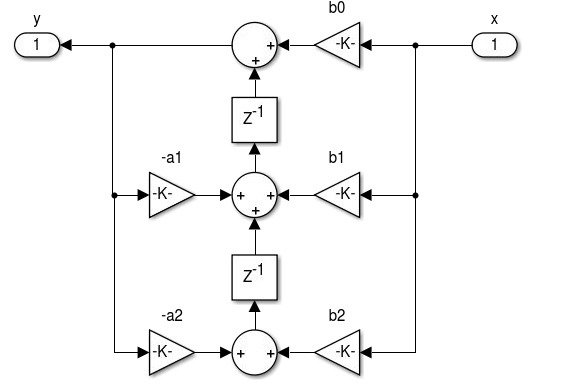
1.5 Uso do Simulink para processamento de sinais
Para aprender o básico do Simulink recomendo assistir a estes vídeos da Mathworks
edit hdlsetup.m
Figura 5.1 - Divisão HDL_DUT e testbench 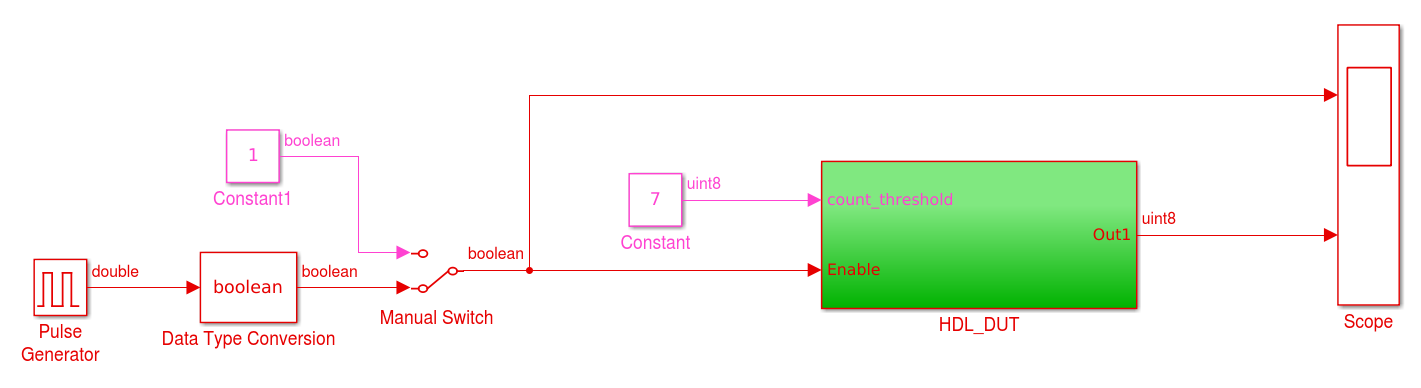 Figura 5.2 - Subsistema HDL_DUT 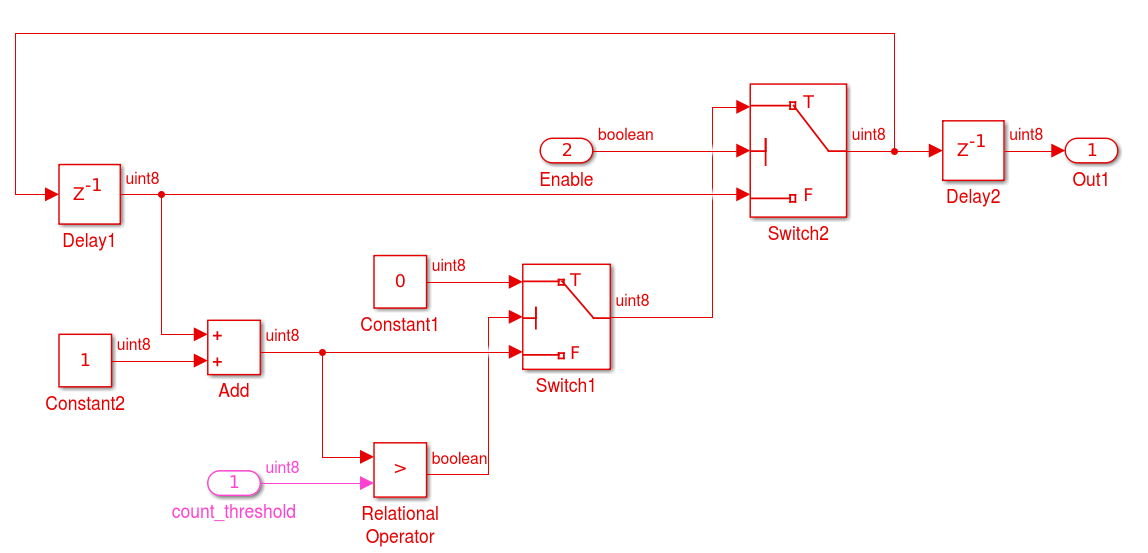
hdlsetup('nome_modelo')
cd hdl_prj/hdlsrc/hdlcoder_simple_up_counter/
do HDL_DUT_compile.do
do HDL_DUT_tb_compile.do
do HDL_DUT_tb_sim.do Figura 5.3 - Subsistema HDL_DUT simulado no Simulink 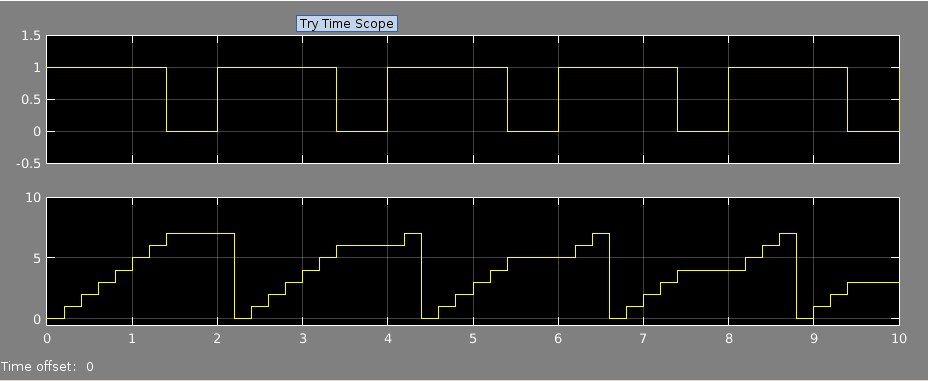 Figura 5.4 - Subsistema HDL_DUT simulado no Modelsim 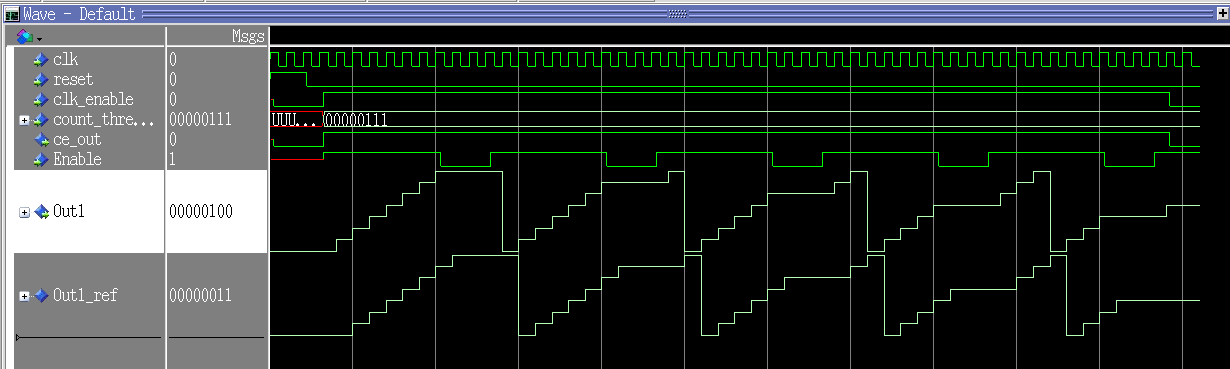
** Note: **************TEST COMPLETED (PASSED)**************
a_sfix = fi(0.1) % 0.1 representado com signed, 16 bits no total com os bits de fração determinados para representar o sinal b_sfix = fi(-0.1) % 0.1 representado com signed, 16 bits no total com 10 bits de fração c_sfix = fi(0.1,1,5,4) % 0.1 representado com signed, 5 bits no total com 4 bits de fração d_sfix = fi(-0.1,1,5,4) % -0.1 representado com signed, 5 bits no total com 4 bits de fração e_sfix = fi(-0.1,0,5,4) % -0.1 representado com unsigned, 5 bits no total com 4 bits de fração => ERRO a_float = 0.1 b_float = -0.1 fi(0:0.3:10,0,8,0) Para observar a precisão da representação mude o formato numérico para format long format hex format short % formato default Experimente com outros números como (10.3 3.25 pi e)
DataMode Type of arithmetic used in quantization. This property can have the following values: fixed — Signed fixed-point calculations float — User-specified floating-point calculations double — Double-precision floating-point calculations single — Single-precision floating-point calculations ufixed — Unsigned fixed-point calculations The default value of this property is fixed. v = -2:0.3:2
q = quantizer('fixed', [5 4])
quantize(q,0.1)
quantize(q,pi)
quantize(q,v)
qu = quantizer('ufixed', [16 4])
quantize(qu,-0.1)
quantize(qu,-pi)
quantize(qu,v)
Note neste caso que a quantidade de bits total e número de casas fracionárias limitam a representação dos números. range(q)
x=-0.2; % Word length = 8, fraction length = 7 q=quantizer([8,7]) range(q) xq=quantize(q,x); binxq=num2bin(q,xq); % Word length = 16, fraction length = 10 q1=quantizer([160 150]) range(q1) xq1 = quantize(q1,x); binxq1=num2bin(q1,xq1); hexxq1=num2hex(q1,xq1); x xq xq1 disp(['x=',num2str(x), ',xq=',num2str(xq), ',bin=', binxq, ',xq1=',num2str(xq1),',bin=', binxq1 ]) format hex xq1 hexxq1 A precisão da representação numérica também varia conforme o numero de bits usados para a parte fracionária. Para saber a precisão (valor correspondente ao bit menos significativo) use a função eps(q). q=quantizer('ufixed', [4,1]);
%q=quantizer([4,1],'fixed')
% q=quantizer([4,0],'ufixed')
% q=quantizer([4,0],'fixed')
% q=quantizer([4,-1],'ufixed')
% q=quantizer([4,-1],'fixed')
tostring(q)
range(q)
eps(q)
xq=quantize(q,x);
binxq=num2bin(q,xq);
xq
binxq
q=quantizer([3 0],'fixed','round','saturate'); quantize(q,0:0.5:16) q=quantizer([3 0],'ufixed','round','saturate'); quantize(q,0:0.5:16) q=quantizer([3 0],'fixed','round','wrap'); quantize(q,0:0.5:16) q=quantizer([3 0],'ufixed','round','wrap'); quantize(q,0:0.5:16) Note a diferença entre estes 4 quantizadores acima.
No caso dos filtros FIR, escolha uma quantidade de bits suficiente para manter a resposta de frequência especificada, ou modifique o filtro visando reduzir o número de bits necessários. No caso dos IIR, utiliza uma estrutura de seções de segunda ordem (SOS) para a implementação dos filtros.
1.5.1 ATUAL
1.5.2 NEXT
|
2 Avaliações
- Atividades extraclasse
| AE1 - Cálculo de uma DFT de comprimento 8 |
|---|
|
| AE2 - Projeto de Filtro Analógico e Filtro Digital IIR (Entrega e prazos ver Moodle) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
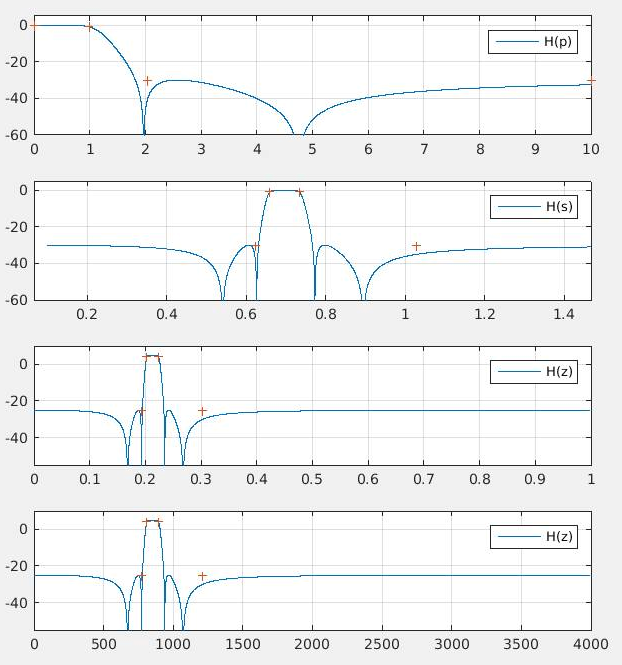
A primeira parte dessa avaliação visa verificar se você conhece a metodologia de projeto de filtros analógicos: (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s), obtendo o filtro LP, HP conforme o tipo de filtro desejado; Nesta avaliação é solicitado que cada equipe realize o projeto de 2 filtros analógicos. Na segunda parte é solicitado que os filtros BP e BS sejam projetados seguindo as etapas (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s) (c) conversão do filtro analógico H(s) em digital H(z), usando a transformação bilinear. Note que nestes casos a frequência de amostragem do sinal e sistema é fundamental no projeto.
|
| AE3 - Projeto de Filtro Digital FIR (Entrega e prazos ver Moodle) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Essa avaliação visa verificar se você conhece a metodologia de projeto de filtros digital FIR com janelas fixas, janelas ajustáveis e usando o algoritmo de Park-McCleallan (PM). Nesta avaliação cada equipe deverá realizar o projeto de 2 filtros analógicos usando janela fixa e ajustáveis e todos os 4 filtros usando o PM. Alguns filtros foram modificados em relação a atividade anterior.
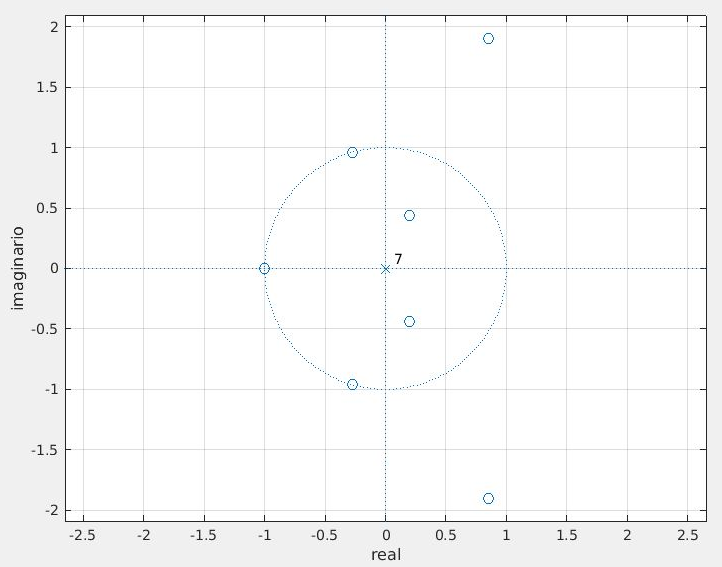
Figura AE3.1 - Resposta ao impulso de um filtro digital FIR 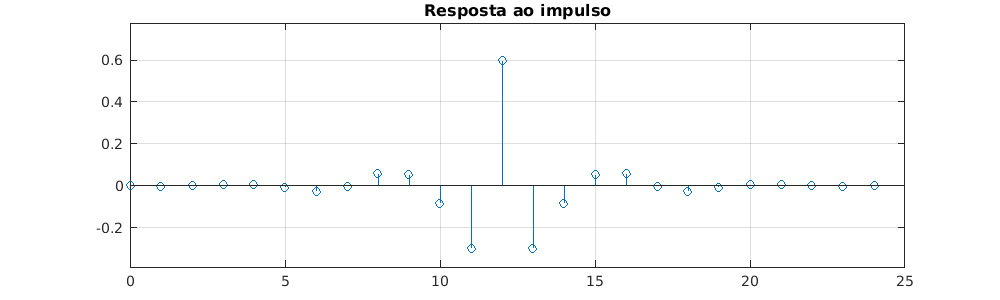 Figura AE3.2 - Resposta em frequência de 3 filtros passa altas do tipo FIR 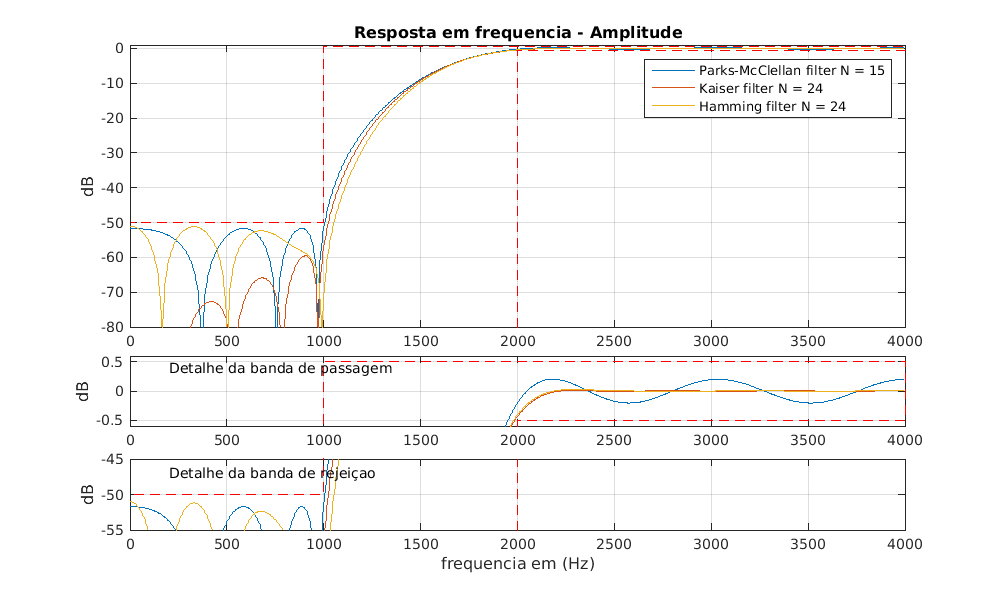 Figura AE3.3 - Diagrama de polos e zeros de um filtro digital FIR 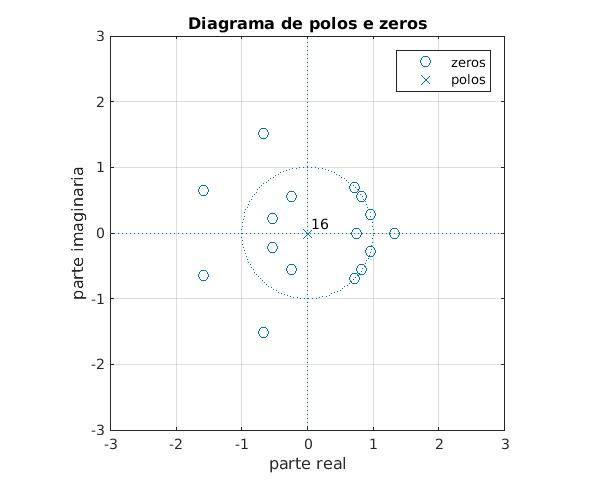 |
| AE4 - Simulação de sistemas DSP com Simulink (Entrega e prazos ver Moodle) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Como atividade de estudo realizar a montagem do modelo indicado na figura abaixo e fazer a simulação, usar fa = 8000Hz.
simulink
fa = 8000 % Sampling frequency; Ta = 1/fa % Sample time; spf = 1 % Samples per frame; v1 = 0.2 % Sine amplitude; f1 = 500 % Sine frequency; G = 0.05 % Gain;
Figura AE4.1 - Modelagem da seleção das fontes de sinal 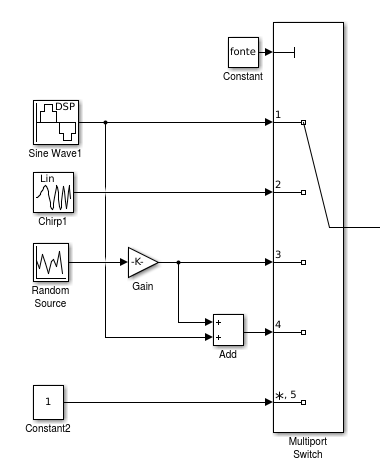
Figura AE4.2 - Modelagem das medições de sinal 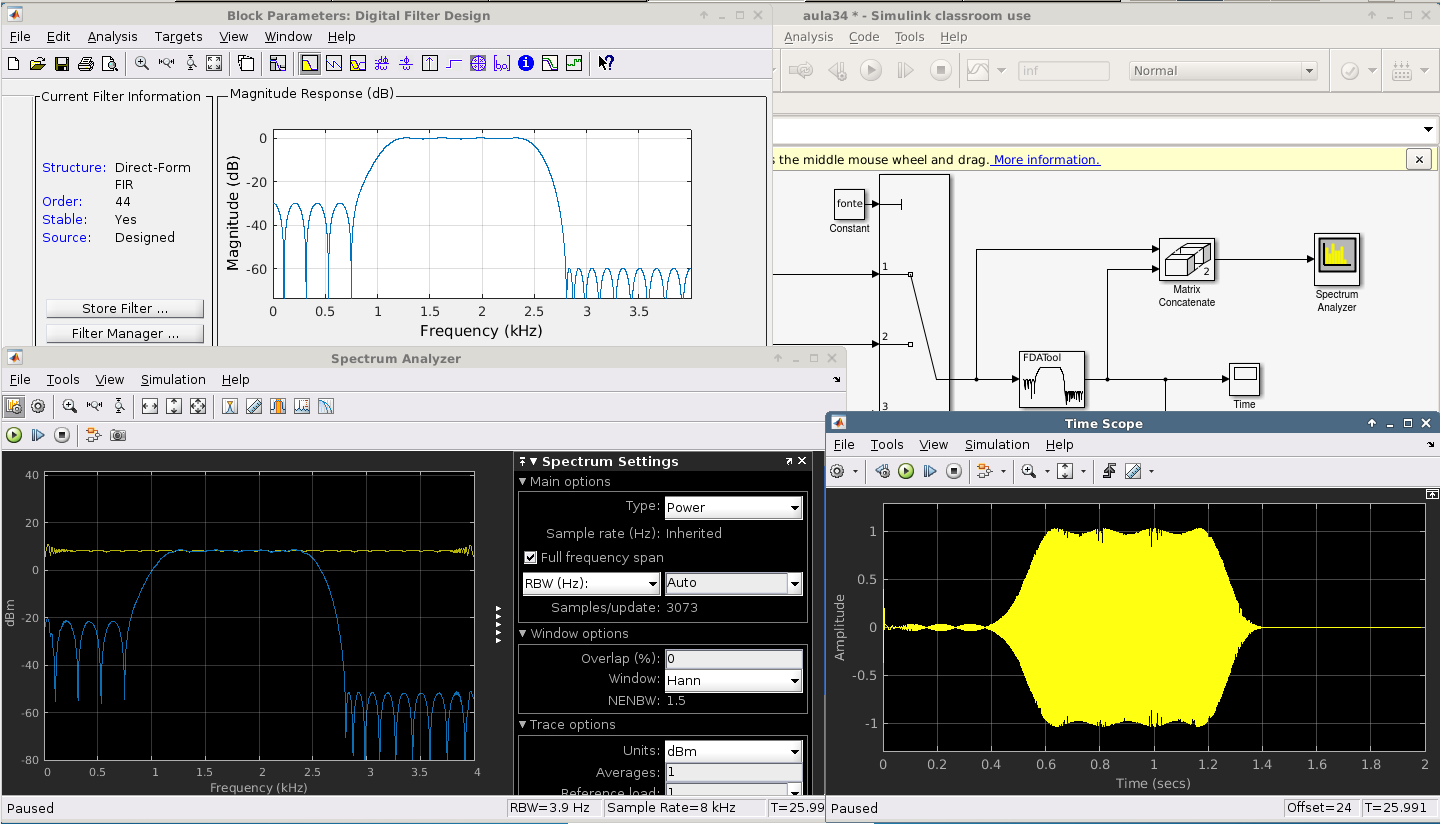
Figura AE4.3 - Modelagem de um sistema em Simulink 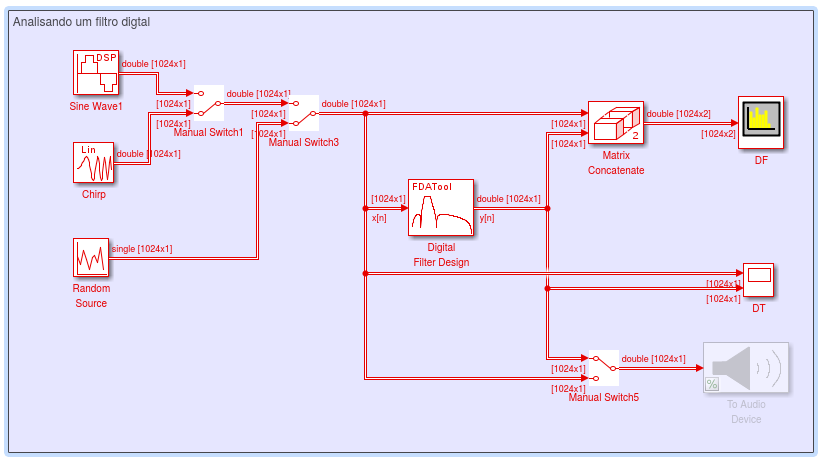 DICAS:
Figura AE4.4 - Análise no DT com fonte de ruído randomico 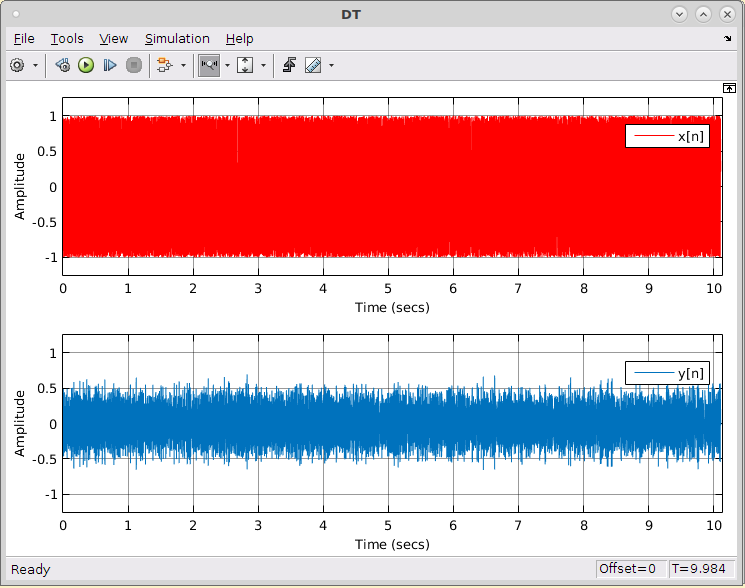 Figura AE4.5 - Análise no DF com fonte de ruído randomico 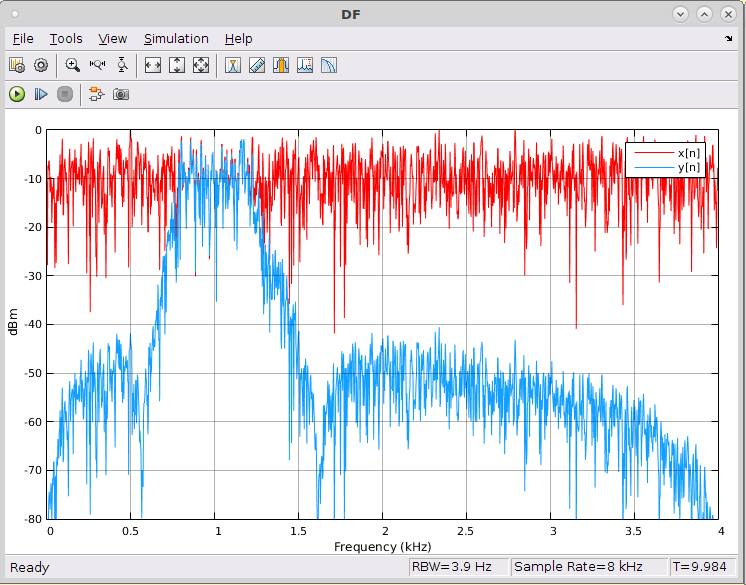
Figura AE4.4 - Análise no DT com fonte de chirp 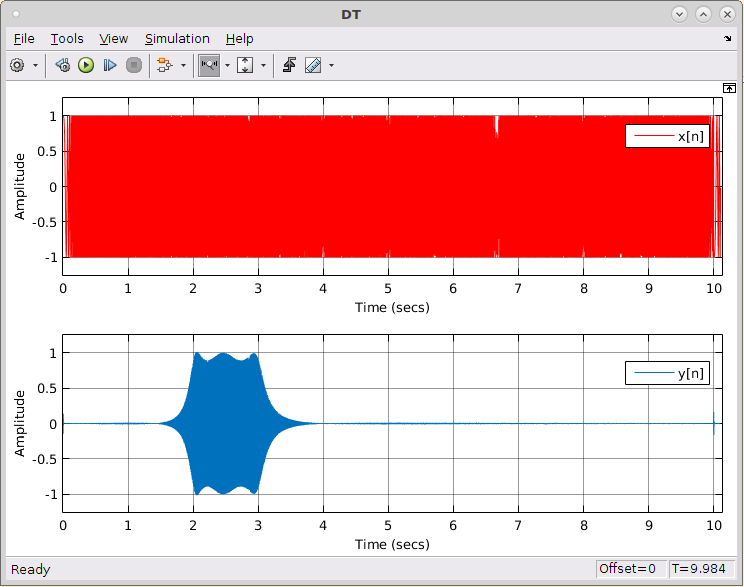 Figura AE4.5 - Análise no DF com fonte de chirp 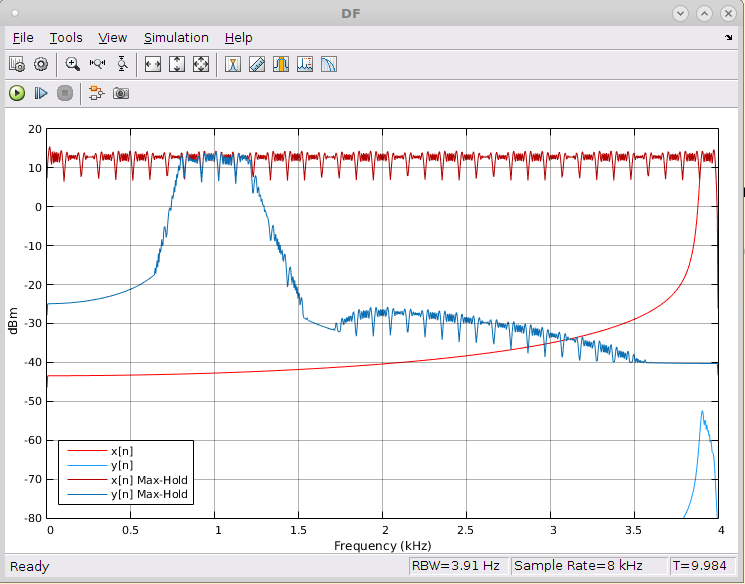 |
2.1 PROJETO FINAL
| PF - Projeto, simulação e realização e implementação em VHDL de filtros | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Em todos os filtros abaixo a especificação será sempre a mesma. Cada equipe deverá utilizar a especificação do Filtro 3 da AE3. Para o filtro FIR poderá ser utilizada a metodologia de projeto de filtros digital FIR com janelas fixas ou janelas ajustáveis ou usando o algoritmo de Park-McCleallan (PM) (APENAS UM DELES). Para o filtro IIR deverão ser seguidas as etapas (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s) (c) conversão do filtro analógico H(s) em digital H(z), usando a transformação bilinear. A aproximação a ser utilizada neste caso pode ser Butterworth, Chebyshev I, Chebyshev II ou Eliptico (Cauer).
(S) Somador = B, (M) Multiplicador = 2B, (D) Delay = B. O número de elementos lógicos o hardware será EL_Hw = N_S x B + N_M x 2B + N_D x B. Multiplicadores por 1, -1, 0, e 2^N não necessitam de hardware para implementação.
|
3 Referências Bibliográficas
- ↑ 1,0 1,1 1,2 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822