ELD129002-Engtelecom (Diário) - Prof. Marcos Moecke

1 Registro on-line das aulas

1.1 Unidade 1 - Aula inicial, Introdução a disciplina

• 1 ENCONTRO

Unidade 1 - Aula inicial, Introdução a disciplina

Encontro 1 (18 mar.) A página da UC contém os materiais que não alteram entre semestre. Relação com as outras UCs do Eixo Sistemas Computacionais (Marrom). Ver grafo do curriculo ELD129002 - ELETRÔNICA DIGITAL I (ELD1): Sistema de numeração e códigos. Lógica booleana. Circuitos combinacionais. Circuitos aritméticos. Linguagem de descrição de hardware. Implementação e teste de circuitos digitais. Projeto de circuitos lógicos. ELD129003 - ELETRÔNICA DIGITAL II (ELD2): Dispositivos lógicos programáveis. Circuitos sequenciais. Metodologia síncrona. Projeto hierárquico e parametrizado. Máquinas de estados finita. Register Transfer Methodology. Teste de circuitos digitais. Implementação em FPGA. Introdução a Linguagem de Descrição de Hardware. AOC129004 - ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES (AOC): Introdução à Arquitetura Computadores. Linguagem Assembly. Linguagem de Máquina. Programação Assembly. Modos de Endereçamento. Processo de compilação e carga de um programa. Introdução à Organização de Computadores. Organização Monociclo e Multiciclo. Pipeline. Memória e Sistema de E/S. MIC129007 - MICROCONTROLADORES (MIC): Introdução a Microcontroladores e Aplicações. Arquitetura de um microcontrolador. Pilha e Subrotinas. Interrupção. Contadores e Temporizadores. Interface com Periféricos. Programação em alto nível (ex.: C, C++ e RUST) para Microcontroladores: Mapeamento de tipos e estruturas de alto nível para sistemas com recursos limitados. Projeto de hardware e firmware com microcontroladores. STE129008 - STE - SISTEMAS EMBARCADOS (STE): Conceitos em Sistemas Embarcados. Metodologia de Desenvolvimento de Sistemas Embarcados. Sistemas Operacionais para Sistemas Embarcados. Ferramentas de desenvolvimento e depuração. Barramentos e dispositivos de acesso a redes. Desenvolvimento de Projeto. Nesta página está o Registro diário dos encontros e avaliações. A entrega de atividades e avaliações será através da plataforma Moodle. A inscrição dos alunos é automática a partir do SIGAA. Para a comunicação entre professor-aluno, além dos avisos no SIGAA, utilizaremos o chat institucional. A princípio todos os alunos já estão previamente cadastrados pelo seu email institucional. Confiram enviando uma mensagem de apresentação. Utilizaremos durante as aulas algumas ferramentas computacionas como o site do Falstad para entender circuitos digitais e fazer simulações básicas. Também utilizaremos os softwares Quartus Light e ModelSim instalados nas maquinas do laboratório para praticar a parte de programação de hardware (descrição de hardware). Esses softwares também podem ser usados através da Nuvem do IFSC.. LER PARA O PRÓXIMO ENCONTRO Capítulo 1. Do Zero ao Um, seções 1.1 a 1.3 do livro David Money Harris, B., & Harris Morgan Kaufman, S. L. (2013). Projeto Digital e Arquitetura de Computadores, diponibilizado gratuitamente pela www.imgtec.com. (#page=27)

1.2 Unidade 2 - Sistema de numeração e códigos

• 4 ENCONTROS

Unidade 2 - Sistema de numeração e códigos

Encontro 2 (20 mar.) O ser humano precisa contar para determinar quantidades de coisas, com as quantidades ele pode fazer operações matemáticas e comparações. Os números permitem representar quantidades de forma simbólica. Os símbolos utilizados são chamados de dígitos. Em alguns sistemas a posição do símbolo faz diferença (sistemas posicionais), enquanto que em outros o símbolo já representa a quantidade. Dependendo do sistema podem existir diferentes tipos e quantidades de símbolos. Sistema decimal É o sistema utilizado no dia a dia das tarefas diárias Utiliza 10 símbolos (dígitos). 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 É um sistema posicional, onde a posição do dígito tem um peso dado pela base (10) elevado ao expoente da posição. Exemplo: o número representado 135, corresponde a 1 centena (10² = 100), 3 dezenas (10¹ = 10) e 5 unidades (10⁰ = 1), pois 1*10² + 3*10¹ + 5*10⁰ = 1*100 + 3*10 + 5*1 = 100 + 30 + 5 = 135 Com o sistema podemos contar quantidades, representar quantidades inteiras e fracionárias, comparar valores (quantidades), fazer operações de soma, subtração, multiplicação, divisão, entre outras; Exemplos: Contar: …, 34, 35, 36, 37, … Somar: 21 + 46 + 100 = 100 + 20 + 40 + 1 + 6 = 100 + 60 + 7 = 167; Multiplicar: 3 x 6 = 6 + 6 + 6 = 18; Dividir: 35/7 = (5+ 5 + 5 + 5 + 5 + 5 +5)/7 = (5*7)/7 = 5; Representar frações: 12/10 = 1,2; 3/4 = 0,75 Comparar valores: 145 > 14,5; 230 = 2,3x10² Outros sistemas: Nos computadores e circuitos digitais, para fazer a representação de números são utilizadas normalmente duas tensões, sendo uma para representar o dígito “0” (0 volt), e outra para representar o dígito “1” ( X volts). Este sistema é chamado de sistema binário, pois utiliza apenas dois dígitos (0 e 1). O sistema também é posicional, e permite representar quantidades e fazer operações matemáticas e comparações OBS: Muitas vezes os números binários são representados através do sistema hexadecimal ou do sistema octal. Uso do Sistema Hexadecimal e Octal Sistema Hexadecimal (Base 16) Computação e Programação: Muito usado para representar cores em HTML/CSS (ex: #FF5733), endereços de memória, e depuração de código em linguagens de baixo nível como Assembly e C. Endereços MAC: Dispositivos de rede usam endereços MAC, que são representados em hexadecimal (ex: 00:1A:2B:3C:4D:5E). Codificação e Criptografia: Muitos algoritmos de criptografia usam representações hexadecimais para armazenar e exibir dados de forma compacta. Representação Binária Compacta: Como cada dígito hexadecimal representa 4 bits, ele é frequentemente usado para simplificar a leitura de valores binários grandes. Sistema Octal (Base 8) Permissões de Arquivos no Linux/Unix: O sistema octal é utilizado para definir permissões de arquivos no formato chmod. No Linux/Unix, cada arquivo tem três tipos principais de permissões: Leitura (r): Permite visualizar o conteúdo do arquivo. Escrita (w): Permite modificar o conteúdo do arquivo. Execução (x): Permite executar o arquivo, se for um programa ou script. Essas permissões são atribuídas a três categorias de usuários: Dono (owner): O usuário que possui o arquivo. Grupo (group): O grupo de usuários associado ao arquivo. Outros (others): Todos os outros usuários. Assim o comando chmod 755, indica que as permissões seriam: Dono: leitura, escrita, execução (rwx = 7) Grupo: leitura, execução (r-x = 5) Outros: leitura, execução (r-x = 5) Sistema binário Utiliza apenas 2 símbolos (dígitos). 0 e 1 É um sistema posicional, onde a posição do dígito tem um peso dado pela base (2) elevado ao expoente da posição. Exemplo 1: o número binário 1112, corresponde a 1 quadra (2² = 4), 1 dupla (2¹ = 2) e 1 unidade (2⁰ = 1). 1*2² + 1*2¹ + 1*2⁰ = 1*4 + 1*2 + 1*1 = 4 + 2 + 1 = 710 Exemplo 2: o número binário 0100101012, corresponde a: 1*27 + 1*24 + 1*22 + 1*20 = 1*128 + 1*16 + 1*4 + 1*1 = 14910 Exemplo 3: o número decimal 11110, corresponde ao número binário 011011112, pois: 1*26 + 1*25 + 1*23 + 1*22 + 1*21 + 1*20 = 64 + 32 + 8 + 4 + 2 + 1 = 11110 O que são bits, nibbles, bytes e word (palavra) de bits ↓msb lsb↓ 0 1 1 0 0 1 1 0 1 1 1 0 0 0 1 1 nibble nibble nibble nibble byte (MSB) byte (LSB) word (palavra) Note no quadro acima: o nibble corresponde ao grupo de 4 bits (meio byte) o byte corresponde ao grupo de 8 bits. Este grupo de 8 bits também é denominado de forma mais exata de octeto. a word corresponde ao grupo de 16 bits (as vezes 32 bits) a double word corresponte ao grupo de 32 bits (as vezes 64 bits) o bit menos significativo (lsb - less significative bit) o bit mais significativo (msb - most significative bit) o byte menos significativo (LSB - Less Significative Byte) o byte mais significativo (MSB - Most Significative Byte) Prefixos e multiplos utilizados para quantidades de informação Nome Símbolo Número de bytes Aproximação decimal Byte B / Byte 1 1 kilobyte kB / kByte $2^{10}$ $10^3$ (mil) Megabyte MB / MByte $2^{20}$ $10^6$ (milhão) Gigabyte GB / GByte $2^{30}$ $10^9$ (bilhão) Terabyte TB / TByte $2^{40}$ $10^{12}$ (trilhão) Petabyte PB / PByte $2^{50}$ $10^{15}$ (quadrilhão) Conversão de bases entre sistemas numéricos Conversão entre os sistemas de numeração decimal - binário - hexadecimal. ver os slides - Sistemas de Numeração: Conversão entre bases PARA O PRÓXIMO ENCONTRO Ler capítulo 1. Do Zero ao Um, seção 1.4 do livro Projeto Digital e Arquitetura de Computadores, diponibilizado gratuitamente pela www.imgtec.com. (#page=34) Rever slides - Sistemas de Numeração: Conversão entre bases Ver mais sobre Byte ou Byte.en e os prefixos binários na Wikipedia Curiosidade Codificação binária 2 entre 5. Encontro 3 (25 mar.) Regra geral de conversão de valor para qualquer sistema de numeração Dividir o valor (número) pela base e obter o quociente e o resto. Dividir sucessivas vezes o quociente anterior até obter um quociente nulo. Os restos obtidos são os digitos que representam o valor (número) no novo sistema de numeração. O primeiro resto obtido é o dígito menos significativo. O último resto obtido é o dígito mais significativo. Passos para a Conversão de Decimal para Binário - divisões sucessivas pela base A conversão de um número decimal (base 10) para binário (base 2) pode ser feita utilizando o método da divisão sucessiva pela base. Esse método é baseado em dividir o número decimal por 2 (a base do sistema binário) e registrar os restos das divisões até o quociente ser igual a zero. O número binário será obtido a partir dos restos dessas divisões, onde o primeiro resto obtido é o bit lsb. Vejamos um exemplo, convertendo o número decimal 1310 para binário. Divida o número 13 por 2: 13 ÷ 2 = 6, resto = 1 (indica que o número não é divisível por 2, portanto é um número IMPAR) Divida o quociente 6 por 2: 6 ÷ 2 = 3, resto = 0 Divida o quociente 3 por 2: 3 ÷ 2 = 1, resto = 1 Divida o quociente 1 por 2: 1 ÷ 2 = 0, resto = 1 O quociente agora é 0, então paramos aqui. Os valores dos restos obtidos, considerando o primeiro resto como lsb (fica a direita), podem ser escrito como: 1 1 0 1. Portanto, o número 1310 em decimal é 11012 em binário. Passos para a Conversão de Decimal para Binário - subtrações sucessivas pelos pesos dos bits A conversão de um número decimal (base 10) para binário (base 2) pode ser feita utilizando o método da subtrações sucessivas. Esse método é baseado em subtrair sucessivamente do número decimal os pesos das potências de 2 e registrar como 1 os pesos que foram subtraidos e como zero quando o número obtido é menor que o peso. Como o método, o primeiro bit obtido é o msb. Vejamos um exemplo, convertendo o número decimal 1310 para binário. Começando com 13. O maior número que é menor ou igual a 13 e que é uma potência de 2 é 8 (23). Então, subtraímos 8 de 13: 13 - 8 = 5 O bit correspondente a (23) é 1. Agora, com 5. O próximo número que uma potência de 2 é 4 (22). Como 5 ≥ 4 subtraímos 4 de 5: 5 - 4 = 1 O bit correspondente a (22) é 1. Agora, com 1. O próximo número que uma potência de 2 é 2 (21). Como 1 < 2 a subtração não pode ser feita e portanto, o bit correspondente a (21) é 0. Agora, com 1 novamente. O próximo número que uma potência de 2 é 1 (20). Como 1 ≥ 1 subtraímos 1 de 1: 1 - 1 = 0 Resultados da Conversão. Agora, temos os bits correspondentes às potências de 2, da maior para a menor: Portanto, o número decimal 1310 é igual ao número binário 11012. Resumo do Processo de Subtração Sucessiva Começamos com 13 e subtraímos as maiores potências de 2 possíveis (8, 4, 2, 1). A cada subtração, associamos um 1 ou 0 ao bit correspondente à potência de 2. O resultado final é o número binário 1101, que é a representação binária de 13. Regra geral de conversão de um sistema de numeração qualquer de base N para decimal Verifique a posição do ponto decimal. Os dígitos a esquerda do ponto decimal correspondem as posições 0, 1, 2, … . Se houver dígitos a direita do ponto decimal, eles correspondem as posições -1, -2, -3, … . A cada dígito é dado um peso correspondente ao valor da base elevada ao expoente Nposição. Multiplique os pesos pelos dígitos correspondentes. O valor final (em decimal) é a soma dos valores obtidos. posição k … 2 1 0 , -1 -2 … -l dígito dk d2 d1 d0 d-1 d-2 d-l peso Nk N2 N1 N0 N-1 N-2 N-l somar dk × Nk d2 × N2 d1 × N1 d0 × N0 d-1 × N-1 d-2 × N-2 d-l × N-l valor dk × Nk + d2 × N2 + d1 × N1 + d0 × N0 + d-1 × N-1 + d-2 × N-2 + d-l × N-l PARA O PRÓXIMO ENCONTRO Resolver exercícios (1.4 a 1.8; 1.13 a 1.20; 1.25 a 1.30; 1.37 a 1.40; 1.43 a 1.49), do livro Projeto Digital e Arquitetura de Computadores, diponibilizado gratuitamente pela www.imgtec.com. (#page=47 no pdf page=73) Encontro 4 (27 mar.) Códigos numéricos binários Número sem sinal (UNSIGNED) Neste caso apenas números inteiros naturais podem ser representados. Usando $N$ bits é possível representar números inteiros no intervalo de $[0,2^N-1]$. Por exemplo usando 8 bits => $[0,2^8-1]=[0,255]=[00000000_2,11111111_2]$ bit 7 6 5 4 3 2 1 0 valor 1 0 1 0 0 1 1 1 peso 27 26 25 24 23 22 21 20 peso +128 +64 +32 +16 +8 +4 +2 +1 somar +128 +32 +4 +2 +1 resultado 128 + 32 + 4 + 2 + 1 = 167 Número com sinal (Sinal-Magnitude ou Magnitude e Sinal) Neste caso os números inteiros negativos são representados com 1 no msb, e o positivos com 0 no msb. Usando $N$ bits é possível representar números inteiros no intervalo de $[-(2^{N-1}-1),(2^{N-1}-1)]$. Nesta representação existem dois zeros, o +0 e o -0. Por exemplo usando 8 bits => $[-(2^{8-1}-1),(2^{8-1}-1)]=[-(2^7-1),(2^7-1)]=[-127,-0,+0,+127]=[11111111_2,10000000_2,00000000_2,01111111_2]$ bit 7 6 5 4 3 2 1 0 peso 26 25 24 23 22 21 20 peso +64 +32 +16 +8 +4 +2 +1 valor 1 0 1 0 0 1 1 1 somar - +32 +4 +2 +1 resultado - ( 32 + 4 + 2 + 1) = - 39 valor 0 0 1 0 0 1 1 1 somar + +32 +4 +2 +1 resultado + ( 32 + 4 + 2 + 1) = +39 Número com sinal (Complemento de 2 ou SIGNED) Neste caso o msb corresponde ao peso negativo, de modo que ao colocar 1 no msb o número inteiro passa a ser negativo, e se o msb for 0, o número será positivo. Usando $N$ bits é possível representar números inteiros no intervalo de $[-2^{N-1},2^{N-1}-1]$. Nesta representação existem apenas um zero. Por exemplo usando 8 bits => $[-2^{N-1},2^{N-1}-1]=[-128,0,+127]=[10000000_2,00000000_2,01111111_2]$ Neste caso note que quando todos os bits são 1, o número representado será o -1, $11111111_2$ bit 7 6 5 4 3 2 1 0 peso -27 26 25 24 23 22 21 20 peso -128 +64 +32 +16 +8 +4 +2 +1 valor 1 0 1 0 0 1 1 1 somar -128 +32 +4 +2 +1 resultado - 128 + 32 + 4 + 2 + 1 = -128 + 39 = -89 valor 0 0 1 0 0 1 1 1 somar +32 +4 +2 +1 resultado 32 + 4 + 2 + 1 = +39 valor 1 1 1 1 1 1 1 1 somar -128 +64 +32 +16 +8 +4 +2 +1 resultado -128 + 64 + 32 +16 + 8 + 4 + 2 + 1 = -128 + 127 = -1 Comparação das representações O quadro abaixo mostra as representações em binário dos valores de +15 a -8 no sistema sem sinal (UNSIGNED), com signal-magnitude , com sinal em complemento de um , com sinal em complemento de dois (SIGNED). No quadro é importante notar que sempre os números negativos tem o msb = 1. Adicionalmente alguns sistemas possuem dois zeros (+0 e -0). No tipo SIGNED note que o valor máximo positivo será menor que o valor absoluto do mínimo negativo, por uma unidade. Representação binária Decimal Sem sinal Sinal-magnitude Complemento de um Complemento de dois +15 1111 — — — +14 1110 — — — +13 1101 — — — +12 1100 — — — +11 1011 — — — +10 1010 — — — +9 1001 — — — +8 1000 — — — +7 0111 0111 0111 0111 +6 0110 0110 0110 0110 +5 0101 0101 0101 0101 +4 0100 0100 0100 0100 +3 0011 0011 0011 0011 +2 0010 0010 0010 0010 +1 0001 0001 0001 0001 +0 — 0000 0000 — 0 0000 — — 0000 −0 — 1000 1111 — −1 — 1001 1110 1111 −2 — 1010 1101 1110 −3 — 1011 1100 1101 −4 — 1100 1011 1100 −5 — 1101 1010 1011 −6 — 1110 1001 1010 −7 — 1111 1000 1001 −8 — — — 1000 Para obter o número negativo em complemento de um deve-se complementar (inverter) todos os bits do número binário positivo. Para obter o número negativo em complemento de dois deve-se: a) obter o complemento de um (complementar (inverter) todos os bits do número binário positivo ); b) somar 1 ao resultado. Para obter o número negativo em sinal-magnitude é necessário apenas adicionar um bit 1 a esquerda do msb. Note que em todos os casos a representação de números com sinal, sempre implica na necessidade de um bit a mais. 13 (decimal) = 1101 (binário sem sinal) +13 (decimal) = 01101 (binário em sinal-magnitude) -13 (decimal) = 11101 (binário em sinal-magnitude) +13 (decimal) = 01101 (binário em complemento de um) -13 (decimal) = 10010 (binário em complemento de um) +13 (decimal) = 01101 (binário em complemento de dois) -13 (decimal) = 10011 = 10010 + 1 (binário em complemento de dois) Código ASCII O código ASCII (American Standard Code for Information Interchange), é um padrão de codificação de caracteres para comunicação digital. Ele tem apenas 128 pontos de código, sendo 95 são caracteres imprimíveis e os demais são não imprimíveis (em azul no quadro abaixo), sendo usados para diversos controles de equipamentos eletrônicos. Atualmente esse código está sendo substituido pelos códigos UNICODE, que tem milhões de pontos de código, mas nos UNICODE os primeiros 128 são iguais ao conjunto ASCII. Código ...0000 ...0001 ...0010 ...0011 ...0100 ...0101 ...0110 ...0111 ...1000 ...1001 ...1010 ...1011 ...1100 ...1101 ...1110 ...1111 …0 …1 …2 …3 …4 …5 …6 …7 …8 …9 …A …B …C …D …E …F 000... 0… NUL SOH STX ETX EOT ENQ ACK BEL BS HT LF VT FF CR SO SI 001... 1… DLE DC1 DC2 DC3 DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS US 010... 2… SP ! " # $ % & ' ( ) * + , - . / 011... 3… 0 1 2 3 4 5 6 7 8 9 : ; < = > ? 100... 4… @ A B C D E F G H I J K L M N O 101... 5… P Q R S T U V W X Y Z [ \ ] ^ _ 110... 6… ` a b c d e f g h i j k l m n o 111... 7… p q r s t u v w x y z { } ~ DEL Ver também [https://www.lookuptables.com/text/ascii-table ASCII Lookup Table Exemplo de leitura do quadro acima: A letra "A" é representado pelo número hexadecimal 41, o que corresponde a 01000001 em binário A letra "a" é representado pelo número hexadecimal 61, o que corresponde a 01100001 em binário O espaço "SP" é representado pelo número hexadecimal 20, o que corresponde a 00100000 em binário Descubra o que está escrito neste código binário onde cada 8 bits correspondem a um simbolo ASCII: 01000010 01101111 01101101 00100000 01100100 01101001 01100001 00100000 01110000 01100101 01110011 01110011 01101111 01000001 01001100 01001100 Código UNICODE O Unicode é capaz de representar uma ampla variedade de caracteres, incluindo caracteres alfabéticos, numéricos, símbolos, caracteres especiais e até mesmo caracteres em idiomas e sistemas de escrita complexos, como chinês, árabe, hindi, hebraico, japonês, emojis entre outros. O Unicode possui um espaço de codificação grande o suficiente para suportar milhares de caracteres diferentes. O Unicode é implementado nos esquemas de codificação UTF-8, UTF-16 e UTF-32. O mais utilizado na web é o UTF-8, por ser eficiente em uso de número de bits e ser compatível com o ASCII. Hoje em dia o UTF-8 é usado em 98% de todos os websites conhecidos [1]. Para cobrir uma vasta gama de caracteres, o Unicode os organiza em blocos. Exemplos de blocos: "Latin basic",Latin-1 Supplement, "Greek and Coptic", "Chess Symbols", "Emoticons", "Mayan Numerals", etc. Ver outros em Unicode Characters and Blocks - Lookup Tables Para testar a conversão de texto para o código UTF-8 use utf8 to hexadecimal converter O processo reverso pode ser feito usando hexadecimal to utf8 converter Para obter o codepoint de uma simbolo ou texto utf8 to code points converter O processo reverso pode ser feito usando code points to utf8 converter PARA O PRÓXIMO ENCONTRO Passos para visualizar os bytes UTF-8 no navegador Abra o Console do Desenvolvedor no navegador No Chrome ou Edge: Pressione F12 ou Ctrl + Shift + I, depois vá para a aba Console. No Firefox: Pressione F12 ou Ctrl + Shift + K para abrir o console diretamente. Digite o seguinte comando no console: new TextEncoder().encode("Ola mundo!") Isso retorna um Uint8Array contendo os bytes em UTF-8. Uint8Array(10) [79, 108, 97, 32, 109, 117, 110, 100, 111, 33, buffer: ArrayBuffer(10), byteLength: 10, byteOffset: 0, length: 10, Symbol(Symbol.toStringTag): 'Uint8Array'] Substitua o a por um "á" (que não está na tabela ASCII) new TextEncoder().encode("Olá mundo!") Isso retorna um Uint8Array contendo os bytes em UTF-8. Uint8Array(11) [79, 108, 195, 161, 32, 109, 117, 110, 100, 111, 33, buffer: ArrayBuffer(11), byteLength: 11, byteOffset: 0, length: 11, Symbol(Symbol.toStringTag): 'Uint8Array'] Note que o "á" (com acento) é representado por dois bytes: 195 161 (ou C3 A1 em hexadecimal), pois está fora da tabela ASCII. Outras opções de visualização seriam: Array.from(new TextEncoder().encode("Olá mundo!")).map(b => b.toString(10).padStart(2, '0')).join(' ') 79 108 195 161 32 109 117 110 100 111 33 Array.from(new TextEncoder().encode("Olá mundo!")).map(b => b.toString(2).padStart(2, '0')).join(' ') 1001111 1101100 11000011 10100001 100000 1101101 1110101 1101110 1100100 1101111 100001 Array.from(new TextEncoder().encode("Olá mundo!")).map(b => b.toString(16).padStart(2, '0')).join(' ') 4f 6c c3 a1 20 6d 75 6e 64 6f 21 Para fazer o contrário, descobrir como o navegador irá apresentar um código UTF-8 console.log(String.fromCodePoint(0x00E1)); O resultado será á Como o UTF-8 codificado? O UTF-8 usa um esquema variável de codificação: Estrutura do UTF-8 Código Unicode Intervalo (Hex) Bytes usados Formato em binário ASCII U+0000 – U+007F 1 byte 0xxxxxxx Latin-1 e outros U+0080 – U+07FF 2 bytes 110xxxxx 10xxxxxx Acima de U+0800 U+0800 – U+FFFF 3 bytes 1110xxxx 10xxxxxx 10xxxxxx Caracteres especiais e emojis U+10000 – U+10FFFF 4 bytes 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx Portanto para os caracteres da tabela ASCII de 0 a 127 (ou códigos UTF-8 U+0000 a U+007F) apenas é colocado um 0 no msb. Para os códigos UTF-8 U+0080 até U+07FF são usados dois bytes: 110xxxxx 10xxxxxx Onde o primeiro byte começa com 110 (indica que usará 2 bytes) e o segundo byte sempre começa com 10 (indicando a continuação dos bits). No caso da letra "á", o código UTF-8 é U+00E1 . Convertendo 00E1 para binário: 00E1 (hex) = 0000 0000 1110 0001 (binário) Desses bits, apenas os 11 bits a direita serão codificados 00011100001 e colocados no lugar dos xxxx, definindo a sequência binária de 16 bits: 110 00011 10 100001 Essa sequência em hexadecimal corresponde a C3A1, ou em decimal C3 => 195, A1 => 161, que é o valor mostrado pelo navegador: Uint8Array(11) [79, 108, 195, 161, 32, Ler capítulo 1. Do Zero ao Um, seção 1.4.6. Números Binários com Sinal em Projeto Digital e Arquitetura de Computadores (no pdf page=43) Resolver exercícios (1.9 a 1.12; 1.21 a 1.24; 1.31 a 1.36; 1.41 a 1.42; 1.50 a 1.51), do livro Projeto Digital e Arquitetura de Computadores (#page=47 no pdf page=73) Encontro 5 (1 abr.) Outros códigos binários: Gray - É um código em que dois valores consecutivos diferem em apenas um bit. Isso é útil para minimizar erros de leitura em sistemas eletrônicos, já que a transição entre estados ocorre com uma única mudança de bit, facilitando a detecção de erros. Note por exemplo: Em código binário convencional o número adjacente a 0111 (7) é o 1000 (8), mudança em 4 bits. Em código Gray o número adjacente a 0100 (7) é o 1100 (8), mudança de apenas 1 bit. One-hot - Neste código cada valor é representado por uma única posição ativa (ALTO) dentro do conjunto de bits, enquanto todas as outras posições estão inativas (BAIXO). Esse código é frequentemente usado em sistemas digitais para representar estados discretos, como em máquinas de estados finitos, e também na geração de sinais de seleção de múltiplos circuitos tais como memórias. A vantagem principal reside na simplicidade da detecção de um único estado ativo, evitando ambiguidades e permitindo uma implementação eficiente em hardware. Johnson - Neste código é gerado deslocando-se sucessivamente todos os bits para a esquerda e colocando o bit complementar do msb como lsb. A codificação normalmente começa com todos bits "0". Devido a sua simplicidade, ele é utilizado para contadores utilizados em controle de sistemas digitais simples de alta velocidade. Por sempre ter apenas 1 bit de diferença entre números adjacentes, ele fornece boa proteção contra erros, mas necessita de mais bits para representar a mesma faixa de valores que um binário sequencial. BCD (Binary-coded decimal) - Esse código basicamente consiste em representar cada digito decimal de 0 a 9 por um grupo de 4 bits (0 -> 0000, 1 -> 0001, ... 8 -> 1000 e 9 -> 1001). Ele é utilizado em mostradores de sete segmentos, onde cada um deles indica um dígito. Decimal Hexadecimal Octal Binário convencional Binário Gray Binário One Hot Binário Johnson BCD 00 0 00 0000 0000 0000.0000.0000.0001 00000000 0000.0000 01 1 01 0001 0001 0000.0000.0000.0010 10000000 0000.0001 02 2 02 0010 0011 0000.0000.0000.0100 11000000 0000.0010 03 3 03 0011 0010 0000.0000.0000.1000 11100000 0000.0011 04 4 04 0100 0110 0000.0000.0001.0000 11110000 0000.0100 05 5 05 0101 0111 0000.0000.0010.0000 11111000 0000.0101 06 6 06 0110 0101 0000.0000.0100.0000 11111100 0000.0110 07 7 07 0111 0100 0000.0000.1000.0000 11111110 0000.0111 08 8 10 1000 1100 0000.0001.0000.0000 11111111 0000.1000 09 9 11 1001 1101 0000.0010.0000.0000 01111111 0000.1001 10 A 12 1010 1111 0000.0100.0000.0000 00111111 0001.0000 11 B 13 1011 1110 0000.1000.0000.0000 00011111 0001.0001 12 C 14 1100 1010 0001.0000.0000.0000 00001111 0001.0010 13 D 15 1101 1011 0010.0000.0000.0000 00000111 0001.0011 14 E 16 1110 1001 0100.0000.0000.0000 00000011 0001.0100 15 F 17 1111 1000 1000.0000.0000.0000 00000001 0001.0101 Extensão de bits de um número inteiro sem sinal Para estender um número de M bits para N bits, basta adicionar (N-M) zeros à esquerda, de modo a ter N bits no total. Exemplo: Estender o número binário sem sinal de 5 bits "01101" para 8 bits: Número original: 01101 = (13 em decimal), pois 8 + 4 + 1 = 13 Número estendido: 00001101 = (13 em decimal), pois 8 + 4 + 1 = 13 Extensão de bits de um número inteiro com sinal em complemento de 2 Para estender um número de M bits para N bits em complemento de 2, o msb (o bit mais significativo) deve ser estendido (copiado) (N-M) vezes para os novos bits à esquerda, de modo a ter N bits no total. Exemplo: Estender o número binário com sinal em complemento de 2 de 5 bits "10011" para 8 bits: Número original: 10011 = (-13 em decimal), pois -16 + 2 + 1 = -13 Número estendido: 11110011 = (-13 em decimal), pois -128 + 64 + 32 + 16 + 2 + 1 = -13 Note que para números positivos o resultado é similar a estender o número inteiro sem sinal. Extensão de bits de um número inteiro com sinal em sinal-magnitude Para estender um número de M bits para N bits do tipo sinal-magnitude, o msb (o bit mais significativo) deve ser movido para o novo msb, e os demais novos bits devem ser zerados. Exemplo: Estender o número binário com sinal em sinal-magnitude de 5 bits "10011" para 8 bits: Número original: 11101 = (-13 em decimal), pois -(+8 + 4 + 1) = -13 Número estendido: 10001101 = (-13 em decimal), pois -(+8 + 4 + 1) = -13 Números binário fracionários em Ponto Fixo A representaçaõ de Ponto Fixo é um número binário que permite representares números fracionários. Os valores são todos escalonados por um fator constante para transformar em um número inteiro. Assim, o número 5,25 pode ser escalonado por 2² => 5,25 x 4 = 21, e portanto 5,25 = 21 / 2². Assim, usando dois bits fracionarios, o número 5,25 pode ser escrito em binário como 10101, onde o separador fracionário esta em 101,01. Usando $M$ bits para representar um número de ponto fixo Q(M,F) com F bits fracionários, é possível representar números fracionários no intervalo de $[0,2^{M-F}-2^{-F}]$. Neste caso a resolução (menor quantidade que se pode representar) é de $2^{-F}$ Por exemplo usando Q(8,3) => $[0;2^5-2^{-3}]=[0;31,875]=[00000,000_2;11111,111_2]$, e a resolução é de $2^{-3}=0,125$. bit 4 3 2 1 0 -1 -2 -3 valor 1 0 1 0 0 1 1 1 peso 24 23 22 21 20 2-1 2-2 2-3 peso +16 +8 +4 +2 +1 +0,5 +0,25 +0,125 somar +16 +4 +0,5 +0,25 +0,125 resultado 16 + 4 + 0,5 + 0,25 + 0,125 = 20,875 Note que que é possível obter rapidamente o valor de um número de ponto fixo, obtendo o valor do seu número inteiro correspondente, dividindo-o por 2-F. No exemplo acima, 10100111, corresponde ao inteiro 167, ou seja se o número é do tipo Q(8,3), o valor é de 167/2-F = 20,875. Assim como nos números inteiros, é possível representar também números em ponto fixo negativos usando complemento de 2 ou sinal-magnitude. PARA O PRÓXIMO ENCONTRO Resolução dos Exercícios 1.7 ao 1.49 Capítulo 1 - Projeto Digital e Arquitetura de Computadores (#page=74) Ler Capítulo 2 - Representações Binárias em Eletrônica digital moderna e VHDL / Volnei A. Pedroni; tradução de Arlete Simille Marques Ver exercícios 2.2 a 2.13, 2.16 a 2.18, 2.21 a 2.26, 2.29 a 2.32, 2.39 a 2.41 de [2] Conversores numéricos Experimente os conversores: Bin, Hex, Dec Converter; Fix-Point <-> Dec Converter; Dec -> IEEE-754 Float/Double Encontro 6 (3 abr.) Ponto Flutuante (floating point) Os números de ponto flutuante são agrupados da esquerda para a direita:1) bit de sinal, 2) expoente e 3) mantissa. Para os formatos binários IEEE 754 (básico e estendido) que possuem implementações de hardware existentes, eles são distribuídos da seguinte forma: Tipo Sinal Exponente Mantissa Total bits   Viés do exponente Precisão em bits Half-precision 1 5 10 16   15 11 Single-precision 1 8 23 32   127 24 Double-precision 1 11 52 64   1023 53 Embora o expoente possa ser positivo ou negativo, em formatos binários ele é armazenado como um número sem sinal que possui um "viés" fixo adicionado a ele. A faixa de expoente para números normais é [−126, 127] para precisão simples, [−1022, 1023] para dupla. Existem três tipos principais de números: normalizados, denormalizados (ou desnormalizados) e especiais (como infinito e NaN - "Not a Number"). Nos formatos IEEE, o bit 1 inicial de um significando normalizado não é realmente armazenado. É chamado de bit "oculto" ou "implícito". Por causa disso, o formato de precisão simples na verdade tem um significando com 24 bits de precisão, o formato de precisão dupla tem 53. O layout para o ponto flutuante de 32 bits e de 64 bits são mostrados abaixo: 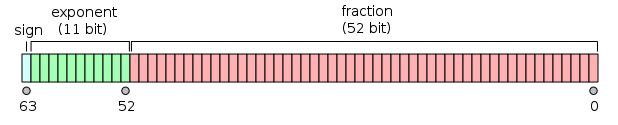Como converter de decimal para floating point? Identifique quantos bits serão usados e obtenha o viés (veja na tabela acima) Converta o número decimal para binário ponto fixo: Normalize a mantissa, movendo o ponto decimal para que haja apenas um um dígito à esquerda do ponto decimal. Determine o sinal, o expoente e a mantissa: 1) O número é positivo, então o bit de sinal é 0. 2) O expoente é o deslocamento necessário para normalizar a mantissa. 3) A mantissa é a parte fracionária normalizada. Converta o expoente para binário com bias: Adicionamos o viés ao expoente para obter o valor final. Junte os bits na ordem: sinal, expoente e mantissa, e obtenha o número em IEEE 754 Floating Point Exemplo: Dado o número 85,125 converta para a representação floating point de 32 bits P1: 32 bits, portanto o viés é 127. P2: 85 em binário é 1010101. 0.125 em binário é 0.001. Portanto, 85,125 em binário é 1010101.001 P3: 1010101.001 => 1.010101001 × 2^6 P4: O número é positivo, então o bit de sinal é 0. O expoente é o deslocamento necessário para normalizar a mantissa. No caso, 6. A mantissa é a parte fracionária normalizada, que é 010101001.(note que o 1 a esquerda do ponto decimal não será representado. P5: Expoente = 6 + 127 = 133 em binário é 10000101. P6: Sinal: 0, Expoente: 10000101, Mantissa: 01010100100000000000000 (completar com zeros até 23 bits), portanto 0 10000101 01010100100000000000000 FONTE: How to Convert a Number from Decimal to IEEE 754 Floating Point Representation Como converter de floating point para decimal? Identifique o número de bits e obtenha o número de bits do expoente e o viés (veja na tabela acima), Obtenha o sinal do número a partir do msb (S = 0 => +; S = 1 => -) Obtenha o número correspondente ao Expoente (E). Considerando o viés, calcule o expoente (e = E - viés) Obtenha o valor da mantissa (M) e Obtenha o valor decimal correspondente, acrescentando o 1 inteiro (se o numero estiver normalizado) antes da conversão O resultado em decimal é $(-{)}^S\times 1.M\times 2^{E-vies}$ Exemplo: Dado o número representado em floating point de 32 bits = 11000000111000000000000000000000 P1: Expoente tem 8 bits => viés = 127 (28-1-1) P2: Sinal (msb): 1 => é um número negativo (-) P3: Expoente (8 bits): 10000001 = 129 P4: expoente (e = E - vies) 129 - 127 = 2 P5: Mantissa: (23 bits): 11000000000000000000000 P6: Valor (24 bits):1.11000000000000000000000 = 1,75 P7: Resultado: (-) 1,75 x 22 = -7 Números sub_normais Os números sub_normais são indicados pelo Expoente = 00000000. Esse Expoente será interpretado como 2-126. Eles, ao contrário dos números normalizados, não usam um "1" implícito no início da mantissa. Isso significa que a mantissa desses números começa com um "0" explícito antes da parte fracionária, permitindo representar valores muito pequenos que não podem ser normalizados devido à limitação dos bits do expoente. Exemplos: 0 00000000 00000000000000000000000 corresponde ao número +0 1 00000000 00000000000000000000000 corresponde ao número -0 0 00000000 10000000000000000000000 corresponde ao número 0,5 x 2-126 = 5.877472E-39 1 00000000 00000000000000000000001 corresponde ao número -2-23 x 2-126 = -0.00000011920928955078125 x 2-126 = -1.40129846432481707092373E-45 (2-149 Números especiais Infinito Positivo (Inf): Bit de sinal: 0 (positivo) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Todos os bits definidos como 0 (23 bits) Representação em 32 bits: 0 11111111 00000000000000000000000 Infinito Negativo (-Inf): Bit de sinal: 1 (negativo) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Todos os bits definidos como 0 (23 bits) Representação em 32 bits: 1 11111111 00000000000000000000000 NaN (Not a Number): Bit de sinal: Pode ser 0 ou 1 (geralmente usado para sinalizar erros ou operações indefinidas) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Pelo menos um bit não nulo (23 bits) Representação: x 11111111 yyyyyyyyyyyyyyyyyyyyyyy (onde "x" é o bit de sinal e "y" são bits da mantissa) Exemplos de conversores online IEEE 754 Calculator 16-bits & 32-bits & 64-bits & 128-bits IEEE-754 Floating Point Converter 32-bitsVer Ponto Fixo e Flutuante - prof. Odilson Ver Floating-point arithmetic - wikipedia Ver IEEE 754 - wikipedia Ler sobre os hardware de microprocessadores [3]. Para ver o número de bits de cada arquitetura, clique no link correspondente na tabela. PARA O PRÓXIMO ENCONTRO Ler 5.3.SISTEMAS NUMÉRICOS (5.3.1. Sistema Numérico de Vírgula Fixa e 5.3.2. Sistemas Numéricos de Virgula Flutuante do livro Projeto Digital e Arquitetura de Computadores (#page=387) Resolver exercicios do livro (1.64 a 1.67, 1.69) Projeto Digital e Arquitetura de Computadores (#page=86) Resolver exercicios do livro (5.24, 5.27 a 5.30, 5.31 a 5.32, 5.38) Projeto Digital e Arquitetura de Computadores (#page=430)

1.3 Unidade 3 - Funções, portas lógicas e álgebra booleana

• 10 ENCONTROS

Unidade 3 - Funções, portas lógicas e álgebra booleana

Encontro 7 (8 abr.) Funções e portas lógicas Funções e portas lógicas PARA O PRÓXIMO ENCONTRO ReverFunções e portas lógicas Ler pag 49 a 69 de Projeto Digital e Arquitetura de Computadores (#page=49) No laboratório remoto do Falstad Laboratórios de Eletrônica Digital, faça os tópicos: Aula de laboratório sobre porta lógicas Aula de laboratório sobre porta lógicas com mais de 2 entradas Encontro 8 (10 abr.) Funções e portas lógicas continuação Funções e portas lógicas PARA O PRÓXIMO ENCONTRO Como as portas lógicas são implementadas com transistores CMOS [[4]] Technology Size Comparison 🤯🤯 3D Animation Quão pequeno é um transistor de 3nm. Sabe como é feito o MicroChip usado nos equipamentos eletrônicos? (apenas os 8 minutos iniciais) How are Microchips Made? 🖥️🛠️ CPU Manufacturing Process Steps (mais detalhado 28 minutos) APOLLO GUIDANCE COMPUTER (AGC) Schematics - Computador de bordo do módulo lunar da Apollo 11, construido usando apenas portas NOR] A computer built from NOR gates: inside the Apollo Guidance Computer Códigos de programação do módulo lunar AGC Assembly Language Encontro 9 (15 abr.) Apresentação da chapa do Zizimo para a Reitoria (40 minutos) Revisão de exercícios sobre sistemas numéricos Encontro 10 (17 abr.) Avaliação A1a - Sistemas numéricos (55 minutos) Álgebra de Boole - slides Para o próximo encontro Rever slides 1 a 15 de Álgebra de Boole Ler a seção 2.3.ÁLGEBRA BOOLEANA nas pag 107 a 116 de Projeto Digital e Arquitetura de Computadores (#page=107) Ler a seção 4-2 LEIS E REGRAS DA ÁLGEBRA BOOLEANA nas pag 201 a 206 de FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 na Minha Biblioteca Estudar a Folha de consulta sobre álgebra booleana para as próximas duas avaliações Encontro 11 (22 abr.) Álgebra de Boole Teoremas de De Morgan O complemento do produto é igual a soma dos complementos: $\overline{X\cdot Y}=\bar{X}+\bar{Y}$ O complemento da soma é igual ao produto dos complementos: $\overline{X+Y}=\bar{X}\cdot \bar{Y}$ Para provar os teoremas, podemos: obter a tabela verdade de ambos lados de cada equação booleana Entradas Saídas X Y $\overline{X+Y}$ $\bar{X}\cdot \bar{Y}$ 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 0 Entradas Saídas X Y $\overline{X+Y}$ $\bar{X}\cdot \bar{Y}$ 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 0 Ou utilizar os postulados e teoremas da algebra de boole PASSO 1: pelo teorema da complementação (T5') $A+\bar{A}=1$, podemos afirmar que $X+Y+\overline{X+Y}=1$ PASSO 2: Considerando que $\overline{X+Y}=\bar{X}\cdot \bar{Y}$ seja verdade $(X+Y)+(\bar{X}\cdot \bar{Y})=1$ PASSO 3: pelo teorema da distribuição (T8') $A+(B\cdot C)=(A+B)\cdot (A+C)$, podemos afirmar que $(X+Y)+(\bar{X}\cdot \bar{Y})=(X+Y+\bar{X})\cdot (X+Y+\bar{Y})$ PASSO 4: pelo teorema da comutatividade (T6') $A+B=B+A$, podemos afirmar que $(X+Y+\bar{X})\cdot (X+Y+\bar{Y})=(Y+X+\bar{X})\cdot (X+Y+\bar{Y})$ PASSO 5: pelo teorema da complementação (T5') $A+\bar{A}=1$, podemos afirmar que $(Y+X+\bar{X})\cdot (X+Y+\bar{Y})=(Y+1)\cdot (X+1)$ PASSO 6: pelo teorema da nulidade (T2') $A+1=1$, podemos afirmar que $(Y+1)\cdot (X+1)=1\cdot 1$ PASSO 7: pelo axioma da multiplicação (A5) $1\cdot 1=1$, podemos afirmar que $1\cdot 1=1$ Portanto a consideração inicial é verdadeira $\overline{X+Y}=\bar{X}\cdot \bar{Y}$. Nota: O teorema também pode ser provado usando o teorema da complementação (T5) $\bar{A}\cdot A=0$, pois neste caso, podemos afirmar que $(X+Y).(\bar{X}\cdot \bar{Y})=0$. Tente desenvolver o restante da prova usando apenas os postulados e teoremas. Usar um circuito lógico para verificar que o teorema é verdadeiro Neste caso, basta analisar as saídas para todas as possíveis entradas. Se a saída sempre for igual o teorema é verificado. Teorema de Demorgan $\overline{X+Y}=\bar{X}\cdot \bar{Y}$. Apesar de termos demostrado um dos teoremas de De Morgam para duas entradas, eles são válidos para qualquer número (N) de entradas, podem ser escritos como: $\overline{X_1\cdot X_2\cdot ...\cdot X_N}=\overline{X_1}+\overline{X_2}+...+\overline{X_N}$ $\overline{X_1+X_2+...+X_N}=\overline{X_1}\cdot \overline{X_2}\cdot ...\cdot \overline{X_N}$ Exercícios Simplifique as expressões lógicas (caso seja possível). Indique os Postulados ou Teoremas utilizado em cada passo. Para simplificar as notações os códigos A1 a A5 e T1 a T12 ou T1' a T12' indicado na folha de consulta sobre álgebra booleana. a) ABC + A + BC b) A.B + A.B’ + A’.B c) X.Y + X.Y’ + X’.Y + X.Y d) X.Y + X.Z + Z.Y e) D.B’+D.(D.B+C.D’) Fazer exercícios 2.13, 2.14, 2.17, 2.18, 2.22, 2.23, pag 127ss Projeto Digital e Arquitetura de Computadores (#page=153) PARA O PRÓXIMO ENCONTRO Ver exemplos em 4-4 ANÁLISE BOOLEANA DE CIRCUITOS LÓGICOS [FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 na Minha Biblioteca Rever slides 16 até fim de Álgebra de Boole Ler a seção 2.3.ÁLGEBRA BOOLEANA nas pag 107 a 116 de Projeto Digital e Arquitetura de Computadores (#page=107) Ler a seção 4-3 TEOREMAS DE DEMORGAN e 4-4 ANÁLISE BOOLEANA DE CIRCUITOS LÓGICOS nas pag 207 a 216 de FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 na Minha Biblioteca Verificar no Falstad algumas das propriedades e teoremas da Algebra de Boole Redundância $X+(X\cdot Y)=X$ Combinação $X\cdot Y+\bar{X}\cdot Y=Y$ Consenso $X\cdot Y+\bar{X}\cdot Z+Y\cdot Z=X\cdot Y+\bar{X}\cdot Z$ Teorema de Demorgan $\overline{X\cdot Y}=\bar{X}+\bar{Y}$ Encontro 12 (24 abr.) Exercícios de algebra booleana Mapa de Karnaugh Encontro 13 (29 abr.) Simplificação de expressões lógicas - Mapas de Karnaugh-Veitch: Ver resumo em Simplificação de expressões lógicas - Mapas de Karnaugh-Veitch Ler a seção 2.7.MAPAS DE KARNAUGH nas pag 99 a 108 de Projeto Digital e Arquitetura de Computadores (#page=125) Para a próxima aula Completar os Mapas de Karnaugh: Realizar o preenchimento dos mapas de Karnaugh para o decodificador de 7 segmentos, considerando os números de 0 a 9. Formar equipes: Organizar equipes de 2 a 3 alunos para desenvolver o projeto de um decodificador de 7 segmentos. Abaixo estão listados 8 conjuntos de informações a serem exibidas no mostrador, correspondentes a cada entrada binária de 0 ("0000") a 15 ("1111"). Cada equipe deverá escolher um conjunto, sendo que nenhum conjunto poderá ser implementado por mais de uma equipe. Figura 3.1 - Conjuntos para mostrador de 7 segmentos Fonte: Elaborado pelo autor. Encontro 16 (6 mai.) Simplificação de expressões lógicas - Mapas de Karnaugh-Veitch: Uso do don't care na simplificação Ver resumo em Simplificação de expressões lógicas - Mapas de Karnaugh-Veitch Ler a seção 2.7.MAPAS DE KARNAUGH nas pag 99 a 108 de Projeto Digital e Arquitetura de Computadores (#page=125) Para a próxima aula Completar os Mapas de Karnaugh: Realizar o preenchimento dos mapas de Karnaugh para o decodificador de 7 segmentos, incluindo os valores conforme conjunto escolhido e também usando don't care para os números de 10 a 15. Preparação da AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos Encontro 17 (8 mai.) Resolver Exercícios de álgebra de Boole Resolver exercicios do livro (2.1, 2.2, 2.5 a 2.10, 2.13 a 2.18, 2.21 a 2.25) Projeto Digital e Arquitetura de Computadores (#page=151) Complementos Ler a seção 2.3.4. A Verdade por Detrás de Tudo e 2.3.5. Simplificando Equações nas pag 87 a 90 de Projeto Digital e Arquitetura de Computadores (#page=113) Ler a seção 2.4. DA LÓGICA ÀS PORTAS e 2.5.LÓGICA COMBINATÓRIO MULTI-NÍVEL nas pag 90 a 95 de Projeto Digital e Arquitetura de Computadores (#page=116) Encontro 18 (13 mai.) Avaliação A1b - Funções e portas lógicas, tabela verdade, algebra de Boole, simplificação de equações e mapa de Karnaugh Encontro 19 (15 mai.) Ver os K-Map online: docjava.com, Departamento de Matemática e Informática da Philipps-Universität Marburg - Alemanha, ICT Laboratory - Cazaquistão Ver soluções de expressões booleanas online: link 1 link2 link3 Como transformar uma Expressão booleana em Tabela verdade e em Circuito com portas lógicas, e vice-versa: Expressão booleana - Tabela verdade - Circuito com portas lógicas Projeto de circuitos combinacionais Para o próximo encontro Ler Quine–McCluskey algorithm Teste em Quine–McCluskey algorithm Ler Espresso heuristic logic minimizer Ler Mapas de Karnaugh 2D e 3D Artigos originais dos métodos M. Karnaugh, "The map method for synthesis of combinational logic circuits," in Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics, vol. 72, no. 5, pp. 593-599, Nov. 1953, doi: 10.1109/TCE.1953.6371932 E. J. McCluskey, "Minimization of Boolean functions," in The Bell System Technical Journal, vol. 35, no. 6, pp. 1417-1444, Nov. 1956, doi: 10.1002/j.1538-7305.1956.tb03835.x Encontro 20 (20 mai.) Como transformar uma Expressão booleana em Tabela verdade e em Circuito com portas lógicas, e vice-versa: Expressão booleana - Tabela verdade - Circuito com portas lógicas Projeto de circuitos combinacionais Encontro 21 (22 mai.) Projeto de circuitos combinacionais: Ver resumo em Projeto de circuitos combinacionais Multiplexadores e Decodificadores: Ler a seção 2.8.BLOCOS COMBINATÓRIOS nas pag 109 a 114 Projeto Digital e Arquitetura de Computadores (#page=135) Encontro 22 (27 mai.) AE2 - Conhecendo os dispositivos lógicos programáveis PASSOS 0, 1 e 2

1.4 Unidade 4 - Introdução a linguagem VHDL e Quartus/ModelSim

• 6 ENCONTROS

Unidade 4 - Introdução a linguagem VHDL e Quartus/ModelSim

Encontro (5 jun.) - Linguagem VHDL Introdução a linguagem de descrição de hardware (DHL) Estrutura do código VHDL Declaração das bibliotecas e pacotes LIBRARY / PACKAGE library library_name; use library_name.package_name.all; ENTITY entity entity_name is [generic ( cons_name1: const_type const_value; cons_name2: const_type const_value; ... cons_nameN: const_type const_value);] [port ( signal_name1: mode signal_type; signal_name2: mode signal_type; ... signal_nameN: mode signal_type);] [declarative_part] [begin statement_part] end [entity] [entity_name]; ARCHITECTURE architecture arch_name of entity_name is [declarative_part] begin statement_part end [architecture] [arch_name]; Exemplo - Declaração de uma porta NAND em VHDL library std; use std.standard.all; entity nand_gate is port (a, b: in bit; x: out bit); end entity; architecture nome_arch of nand_gate is begin x <= a nand b; end architecture; Uso do ambiente EDA - QUARTUS Prime para programação em VHDL PARA O PRÓXIMO ENCONTRO Escreva em VHDL o circuito do AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos Use como modelo: -- A bibliteca std e o pacote standard são autodeclarados, então as linhas abaixo podem ser comentadas com "--" --library std; --use std.standard.all; entity BCD2SSD is port ( -- Entradas ABCD do circuito A, B, C, D: in bit; -- Saidas para os leds do mostrador de 7 segmentos. Note que o nome a, b, .. g foi mudado para ssd_a, ssd_b, ... ssd_g pois o VHDL é insensível a caixa ssd_a, ssd_b, ssd_c, ssd_d, ssd_e, ssd_f, ssd_g : out bit ); end entity; architecture ifsc_v1 of BCD2SSD is begin -- descreva a expressão lógica obtida para cada uma das saídas; -- Por exemplo: se for a = A + C + (B'.D') + (B.D) ssd_a <= A or C or (not B and not D) or (B and D); ssd_g <= ; end architecture; Ler VHDL na Wikipedia. Guardar Folha de consulta de VHDL Encontro (10 e 12 jun.) AE3 - Programação do kit Mercurio IV PARA O PRÓXIMO ENCONTRO ver Preparando para gravar o circuito lógico no FPGA. ver Como arquivar um projeto. ver Simulação Funcional usando o ModelSim. ver Como utilizar a matriz de leds do kit Mercurio IV da Macnica - caso alguém deseje acender os leds conforme as chaves de entrada são selecionados. ver Como_transferir_arquivos_entre_o_computador_local_e_a_NUVEM-IFSC. ver Como configurar o X2Go para acessar a nuvem de seu computador pessoal. ver Programando o kit FPGA usando comando de linha. Consultar e guardar a Folha de consulta de VHDL Ler a seção História da página VHDL da wikipedia em português e as seções History, Standardization}, [https://en.wikipedia.org/wiki/VHDL#Design Design e Advantages da página VHDL na Wikipedia em ingles.

1.5 Unidade 5 - Circuitos lógicos combinacionais (com VHDL)

• 12 ENCONTROS

Unidade 5 - Circuitos lógicos combinacionais (com VHDL)

Encontro 26 e 27 (24 e 26 jun.) Conhecer o Código Gray Implementação de conversor Binário para Gray (bin2gray) ------------------------- -- File: bin2gray_v1.vhd -- ------------------------- entity bin2gray_v1 is port ( b0, b1, b2, b3 : in bit; g0, g1, g2, g3 : in bit ); end entity; --Exemplo implementando o circuito diretamente com as portas lógicas architecture ifsc_v1 of ____ is begin end architecture; Como o circuito de um conversor bin2gray, possui uma certa quantidade de bits de entrada e a mesma quantidade de saída, não é adequado descrever esse circuito utilizando o tipo bit. O VHDL dispõe do tipo bit_vector; de vetores para descrever esse tipo de entrada e saída. ------------------------- -- File: bin2gray_v2.vhd -- ------------------------- entity bin2gray_v2 is port ( b : in bit_vector(3 downto 0); g : out bit_vector(3 downto 0) ); end entity; --Exemplo implementando o circuito diretamente com as portas lógicas architecture ifsc_v2 of ____ is begin end architecture; Caso se deseje aumentar o número de bits da entrada, na abordagem acima é necessário aumentar o número de operações ou exclusivo, e para cada quantidade de bits é necessário ter uma nova descrição. Usando corretamente a instrução generic, e a instrução for generate, é possível escrever um código único (genérico) para qualquer numero de bits. O GENERIC permite parametrizar um circuito, definindo os valores que se deseja alterar em um circuito em diferentes soluções. Um exemplo comum é alterar o número de bits das entradas e saídas do circuito. Essa instrução é declarada na ENTITY, antes da declaração das PORT. [generic ( cons_name1: const_type const_value; cons_name2: const_type const_value; ... cons_nameN: const_type const_value);] Uso da instrução FOR-GENERATE label: FOR identificador IN faixa GENERATE [Parte_Declarativa BEGIN] Instruções_concorrentes ... END GENERATE [label]; ------------------------- -- File: bin2gray_v3.vhd -- ------------------------- entity bin2gray_v3 is generic (N : natural := 4 ); port ( b : in bit_vector(N-1 downto 0); g : out bit_vector(N-1 downto 0) ); end entity; architecture ifsc_v3 of ____ is begin end architecture; Após cada implementação analise o diagrama RTL e verifique se as 3 soluções apresentadas resultam no mesmo circuito. Efetua a simulação com o Modelsim para verificar se as entradas em código binário sequêncial de "0000" até "1111" resultam corretamente nas saídas em Código Gray. Verifique se a versão bin2gray_v3 pode ser alterada para 10 bits e continua gerando o circuito correto. Descubra quantas portas ou exclusivo seriam necessárias para o caso de N bits. Implemente um conversor Gray para Binário (gray2bin): Considerando o que aprendeu com as versões do conversor bin2gray, descreva o circuito do conversor gray2bin. Inicie descrevendo o código VHDL para 4 bits, em seguida busque tornar o código genérico para qualquer número de bits. ------------------------- -- File: gray2bin.vhd -- ------------------------- entity gray2bin is generic (N : natural := 4 ) port ( g : in std_logic_vector(____) b : out std_logic_vector(____) ) end entity architecture ifsc_v1 of ____ is begin end architecture architecture ifsc_v2 of ____ is begin end architecture Implementação de incrementador Gray (inc_gray) O circuito deve usar uma entrada Gray de N bits, e retornar na saída o valor em Gray incrementado. Por exemplo: g_in = 100110 (59) g_out = 100010 (60) A solução sugerida foi: Converter a entrada de Gray para binário Incrementar em binário Converter de binário para Gray Por exemplo: g_in = 100110 (59) b_in = 111011 (59) b_in + 1 = 111100 (60) b_out = 111100 (60) g_out = 100010 (60) ------------------------- -- File: inc_gray.vhd -- ------------------------- entity inc_gray is port ( g_in : in std_logic_vector(3 downto 0); g_out : out std_logic_vector(3 downto 0) ); end entity; architecture ifsc_v1 of inc_gray is signal bin : std_logic_vector(3 downto 0); signal bin_inc : std_logic_vector(3 downto 0); begin -- Converter a entrada de g_in para b_in -- código visto e aula anterior -- Incrementar e binário b_out = b_in + 1 -- aqui falta conhecimento de linguagem para fazer. -- Converter a entrada de b_out para g_out -- código visto e aula anterior end architecture; O problema nesta solução é como fazer o incremento de um número em binário. Será necessário aprender: somar em binário, pois incrementar é somar 1. -- necessário usar os pacotes std_logic_1164 e numeric_std da biblioteca ieee library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; -- Declare um signal do tipo unsigned para usar operador aritmético sobre ele signal bin_uns : unsigned(3 downto 0); -- converta o valor binário para unsigned bin_uns <= (unsigned(bin)); bin_inc <= std_logic_vector(bin_uns + 1); architecture ifsc_v1 of inc_gray is signal b_in  : std_logic_vector(3 downto 0); signal b_inc  : std_logic_vector(3 downto 0); begin -- Converter a entrada de g_in para b_in -- código visto e aula anterior -- Incrementar e binário b_out = b_in + 1 -- aqui falta conhecimento de linguagem para fazer. -- Converter a entrada de b_out para g_out -- código visto e aula anterior end architecture; </syntaxhighlight> os tipos de dados que permitem fazer operações aritméticas em binário, como fazer a conversão entre tipos de dados em VHDL (integer, bit_vector, std_logic_vector, unsigned). Fica a pergunta. Seria possível fazer o incremento direto em gray sem passar primeiro para o binário? Tente encontrar alguma solução observando a regra de mudança dos bits no código Gray. Não esqueça que apenas o valor atual da entrada é conhecido. Encontro 28 (1 jul.) Conhecer o multiplexador digital. Um multiplexador digital de N entradas e 1 saída, frequentemente abreviado como MUX N:1, é um circuito digital muito utilizado para rotear sinais digitais. Ele desempenha a função de selecionar uma das entradas para ser encaminhada para a saída com base em um sinal de seleção (ou controle). MUX2:1 A tabela verdade que descreve um MUX2:1 é mostrada abaixo: X1 X0 Sel Y 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 O MUX2:1 também pode ser representado de forma resumida por: X1 X0 Sel Y - X0 0 X0 X1 - 1 X1 onde o X0 e X1 na entrada podem assumir os valores 0 ou 1, e o simbolo "-" corresponde ao don't care (em VDHL) A função booleana que descreve a operação de um MUX 2:1 pode ser representada da seguinte forma: $Y=\overline{Sel}.X0+Sel.X1$ Onde Y é a saída; Sel é o sinal de seleção; X0 e X1 são as entradas. MUX4:1 O MUX4:1 pode ser representado de forma resumida pela tabela verdade: Entradas Seleção Saída X3 X2 X1 X0 Sel1 Sel0 Y - - - X0 0 0 X0 - - X1 - 0 1 X1 - X2 - - 1 0 X2 X3 - - - 1 1 X3 A função booleana que descreve a operação de um MUX 4:1 pode ser representada da seguinte forma: $Y=X0.\overline{Sel1}.\overline{Sel0}+X1.\overline{Sel1}.Sel0+X2.Sel1.\overline{Sel0}+X3.Sel1.Sel0$ Dada a função booleana do MUX4:1 é simples para descreve-lo em VHDL utilizando apenas operadores lógicos. entity mux4x1 is port ( X: in bit_vector (3 downto 0); -- Quando X é declarado como bit_vector (3 downto 0) -- ordem dos bits | X(3) | X(2) | X(1) | X(0) | -- X(0) é o bit mais a direita do vetor X, X(3) é o bit mais a esquerda do vetor X. -- X: in bit_vector (0 to 3); -- Se X é declarado como bit_vector (0 to 3) -- ordem dos bits | X(0) | X(1) | X(2) | X(3) | -- X(3) é o bit mais a direita do vetor X, X(0) é o bit mais a esquerda do vetor X. Sel : in bit_vector (1 downto 0); Y : out bit ); end entity; -- Implementação com lógica pura architecture v_logica_pura of mux4x1 is begin Y <= (X(0) and (not Sel(1)) and (not Sel(0))) or (X(1) and (not Sel(1)) and Sel(0)) or ... -- continue para X(2) e X(3) end architecture; No entanto, o MUX4:1 também pode ser descrito utilizando a instrução WHEN-ELSE <optional_label>: <target> <= <value> when <condition> else <value> when <condition> else <value> when <condition> else ... <value>; Importante: O último ELSE deve cobrir todos os demais valores para evitar a criação de LATCHES. Warning (13012): Latch ... has unsafe behavior No Quartus Prime SE existe um template pronto para ser utilizado em: [Edit > Insert Template > Language templates = VHDL (+) > Constructs (+) > Concurrent Statemens (+) > Conditional Signal Assignment] Exemplo do mux4x1 implementado com WHEN ELSE -- Implementação com WHEN ELSE architecture v_WHEN_ELSE of mux4x1 is begin Y <= X(0) when Sel = "00" else X(1) when Sel = "01" else X(2) when Sel = "10" else X(3); end architecture; Outra forma de descrever o MUX4:1 seria utilizando a instrução WITH-SELECT <optional_label>: with <expression> select <target> <= <value> when <choices>, <value> when <choices>, <value> when <choices>, ... <value> when others; Importante: Para cobrir todas as demais possibilidades deve ser utilizado o WHEN OTHERS evitando novamente a criação de LATCHES, ou erros de análise. Error (10313): VHDL Case Statement error ...: Case Statement choices must cover all possible values of expression No Quartus Prime SE existe um template pronto para ser utilizado em: [Edit > Insert Template > Language templates = VHDL (+) > Constructs (+) > Concurrent Statemens (+) > Selected Signal Assignment] Exemplo do mux4x1 implementado com WITH SELECT -- Implementação com WITH SELECT architecture v_WITH_SELECT of mux4x1 is begin with Sel select Y <= X(0) when "00", -- note o uso da , X(1) when "01", X(2) when "10", X(3) when others; -- note o uso de others, para todos os demais valores. -- Não pode ser substituido por "11" mesmo que o signal seja bit_vector. end architecture; Note que para associar uma entre várias arquiteturas com a sua ENTITY pode-se utilizar a instrução CONFIGURATION. No exemplo abaixo a ARCHITECTURE que está descomentada é a que será associada a ENTITY mux4x1. Caso não se use a instrução CONFIGURATION, a última ARCHITECTURE será associada a ENTITY. Apesar de apenas uma das ARCHITECTUREs ser associada, todas elas devem estar sintaticamente corretas, pois passarão pelo processo de ANÁLISE E SINTESE. -- Design Unit que associa a architecture com a entity configuration cfg_ifsc of mux4x1 is for v_logica_pura end for; -- for v_WHEN_ELSE end for; -- for v_WITH_SELECT end for; end configuration; Faça a análise e sintese do mux4x1, associando a architecture v_logica_pura, depois v_WITH_SELECT, depois v_WHEN e por último v_IF_ELSE. Note a diferença entre os RTL Viewer obtidos para cada architecture. Figura 2.1 - Código RTL do mux4x1 v_logica_pura 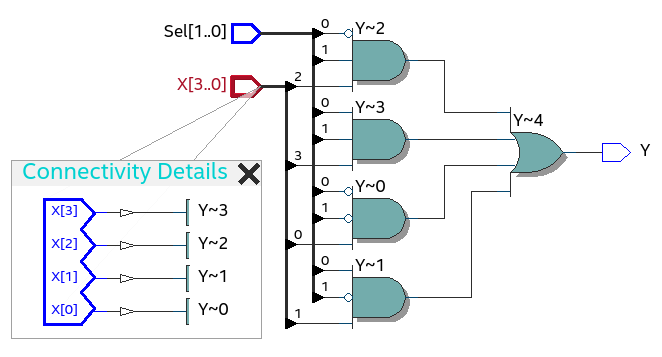Fonte: Elaborado pelo autor. Figura 2.2 - Código RTL do mux4x1 v_WHEN_ELSE 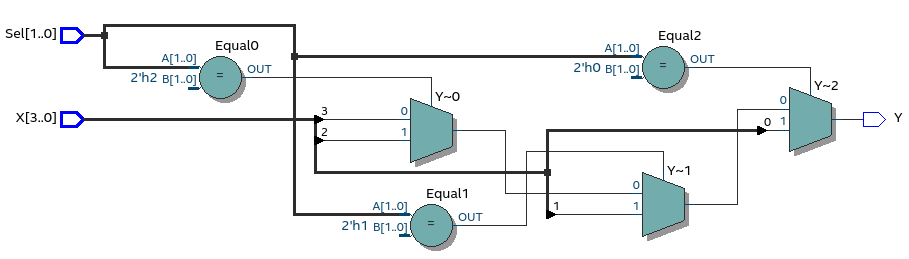Fonte: Elaborado pelo autor. Figura 2.3 - Código RTL do mux4x1 v_WITH_SELECT 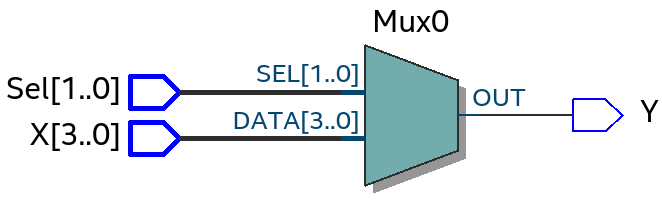Fonte: Elaborado pelo autor. OBS: Register Transfer-Level (RTL) é uma abstração na qual o circuito é descrito em termos de fluxo de sinais entre os registradores presentes no hardware e as operações combinacionais realizadas com esses dados. Note a que ao verificar o Technology Map Viewer, nos 3 primeiros casos serão usados os mesmos elementos lógicos. Figura 2.4 - Technology Map do mux4x1 para a família Cyclone 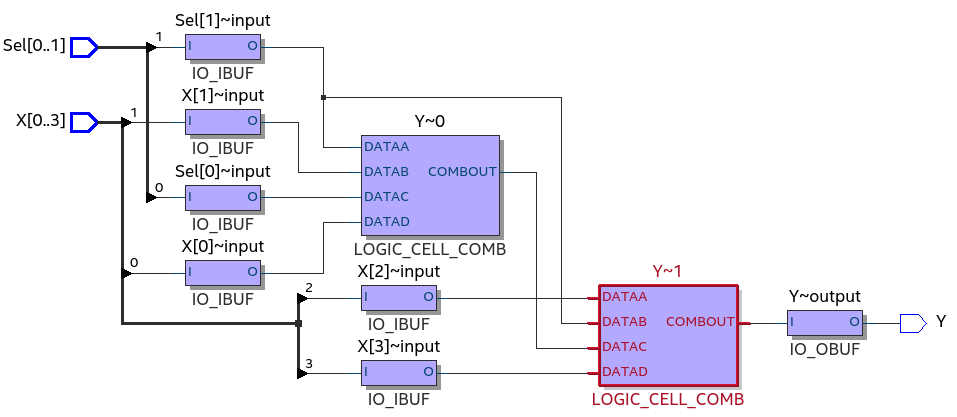Fonte: Elaborado pelo autor. Note que o elemento lógico acima possui uma LUT (LookUp Table) que basicamente implementa o circuito combinacional através de uma tabela de consulta (Tabela Verdade), a qual pode ser visualizada clicando com o botão Direito do Mouse e selecionando Properties, juntamente com Mapa de Karnaugh e seu Circuito Lógico representado por portas. Todas as representações são equivalentes. Figura 2.5 - Elemento Lógico usado no mux4x1 para a família Cyclone (node properties) 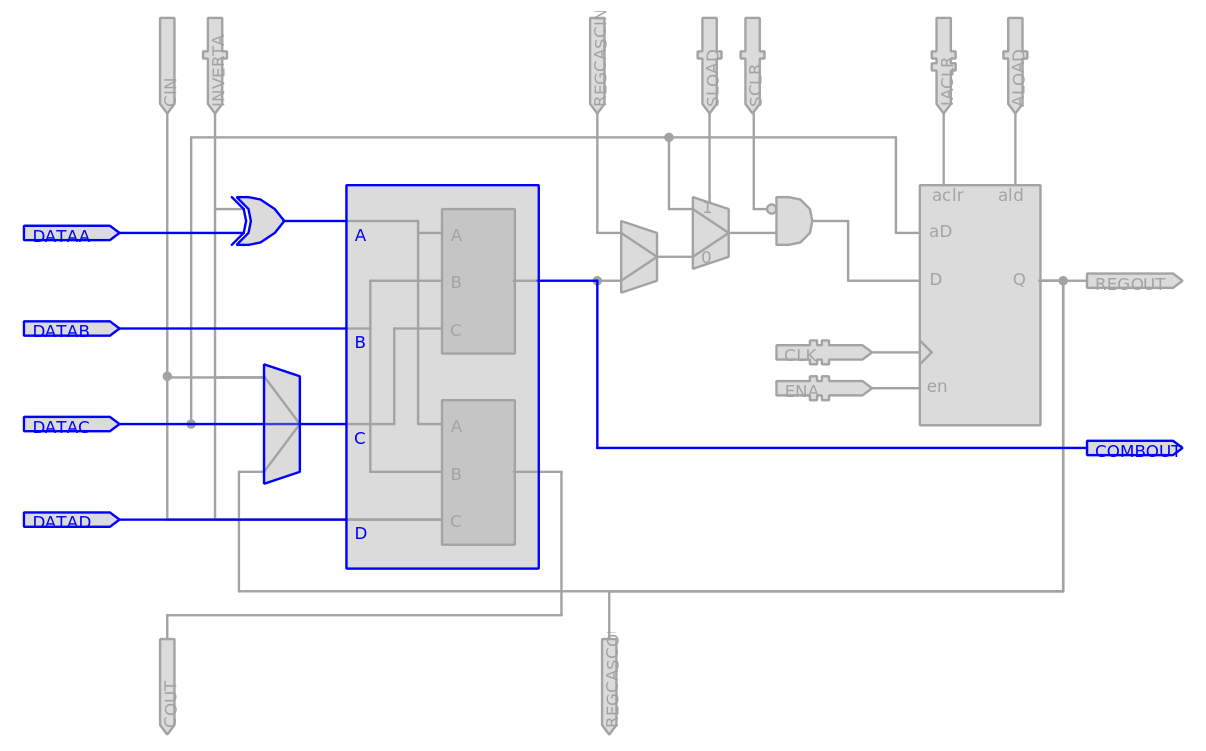Fonte: Elaborado pelo autor. Dependendo da família de FPGA que se estiver usando, o compilador implementar o circuito descrito com um número diferente de elementos lógicos (LEs). No caso da família Cyclone, na qual a LUT tem 4 entradas, são necessários 2 LEs para mapear uma lógica combinacional com 6 entradas e 1 saída (Mux4x1). No entanto se utilizarmos um dispositivo FPGA da família Aria 10, que tem LUT tem 6 entradas, será necessário apenas 1 LE, conforme ilustrado a seguir. Figura 2.6 - Technology Map do mux4x1 para a família Aria 10 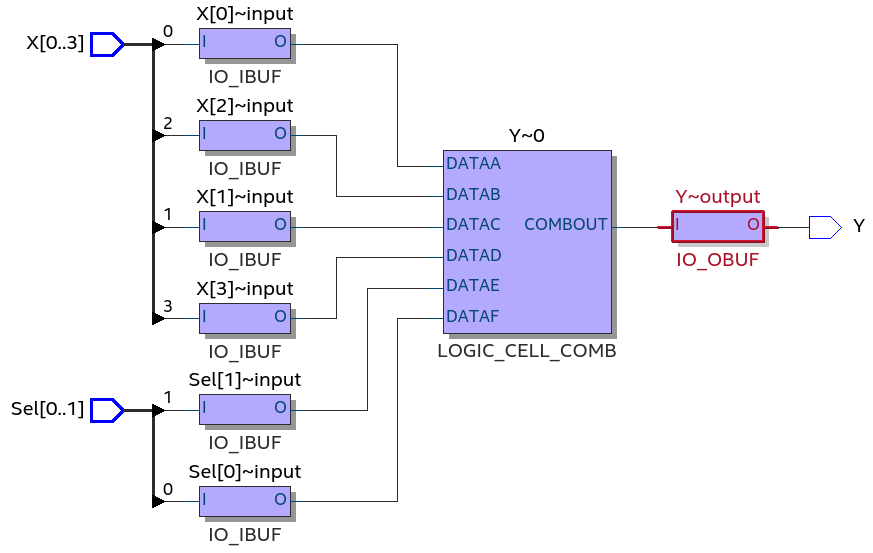Fonte: Elaborado pelo autor. Encontro 29 (3 jul.) Avaliação A1c. 1.5.1 ATUAL Encontro 30 (8 jul.) Implementar o conversor de bcd para ssd usando: A instrução with select A instrução when else Faça a implementação de um conversor de binário para ssd que forneça na saída as seguintes letras: Figura 5.20 - Alfabeto usando mostrador de 7 segmentos 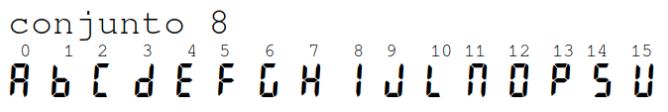Fonte: Elaborado pelo autor. Use o kit Mercúrio IV para implementar o hardware. As chaves SW0 a SW3 devem ser usadas como as entradas binárias bin(0) a bin(3), e o display de sete segmentos DISP0 como saída ssd(0) a ssd(6).

1.6 Unidade 6 - Circuitos aritméticos (com VHDL)

• 5 ENCONTROS

Unidade 6 - Circuitos aritméticos (com VHDL)

2 Avaliações

Durante o semestre serão realizadas 4 avaliações. As avaliações devem ser enviadas pela plataforma Moodle com os arquivos solicitados.

Data das avaliações

• A1a - (3 pontos) Sistema de Numeração e códigos : 17/04/2025
• A1b - (4 pontos) Expressões lógicas e mapa de Karnaugh : 13/05/2025
• A1c - (4 pontos) Circuitos lógicos, Introdução ao VHDL e revisão de A1a e A21b() :
• A2a - (5 pontos) Circuitos combinacionais :
• A2b - (5 pontos) Circuitos aritméticos :
• R12 - Recuperação de A1 a A2 :

Folhas de consulta:

• A1b, A1c Álgebra booleana
• A2a, A2b Tabelas das figuras 3.6, 3.10 e 4.1 do livro do Pedroni.
• A2b Conversões do pacote numeric_std ou Conversões do pacote numeric_std (DOULOS)

3 Atividade relâmpago (AR)

As atividades relâmpago devem ser entregues no Moodle da disciplina. A não entrega dessas atividades não gera nenhum desconto, apenas geram pontos de BÔNUS que são adicionados aos conceitos das avaliações A1 a AN.

4 Atividade extra-classe (AE)

A média ponderada das atividades extra-classe será considerada no cálculo do conceito final da UC. A entrega das mesmas será feita pelo Moodle, e cada dia de atraso irá descontar 0,2 na nota da atividade. Muitas dessas atividades também geram pontos de BÔNUS que são adicionados aos conceitos das avaliações A1 a AN. Para os BÔNUS só serão considerados projetos entregues no prazo.

4.1 AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos

AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos

Objetivos Conhecer o mostrador (diplay) de 7 segmento Projetar um circuito digital que realize a conversão de uma entrada binária de 4 bits para uma saída de um mostrador de 7 segmentos, para o conjunto escolhido. Descrever o funcionamento de um circuito através de uma tabela verdade. Usar a técnica do mapa de Karnaugh para minimizar a função lógica de cada uma das saídas. Atividades Veja como funciona o Display de 7 segmentos. Veja os conjuntos disponíveis: Figura AE1.1 - Conjuntos para mostrador de 7 segmentos Fonte: Elaborado pelo autor. Nesta atividade os estudantes devem projetar um conversor de binário para mostrador de 7 segmentos. Inicialmente considere que na entrada são possíveis apenas os valores 0, 1, 2, ... 8, 9. Apesar de uma entrada binária de 4 bits poder receber os valores 1010 (dez), 1011 (onze), ... 1111 (quinze), pode considerar que elas não acontecem por restrição dos dados de entrada. Por isso, cada estudante tem a liberdade de definir como o mostrador se comportará nesta situação. Digito ABCD ssd_a ssd_b ssd_c ssd_d ssd_e ssd_f ssd_g Mostrador 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 A 1010 B 1011 C 1100 D 1101 E 1110 F 1111 Em um novo projeto considere que os valores 1010 (dez), 1011 (onze), ... 1111 (quinze) mostram os segmentos acessos conforme figura acima. Entregas O projeto todo deverá se realizado manuscrito, devendo as folhas ter a identificação do nome completo do estudante e estar grampeadas. Devem ser feitos dois projetos, sendo que um deve usaro o don't care e outro usando todas as entradas conforme o conjunto escolhido. Compare o resultado final dos dois projetos. Deverão ser apresentados no mínimo: 1) A tabela verdade completa indicando para as entradas de 0 a 15 quais são os valores das saídas (segmentos) a, b, c, d, e, f, g. 2) Para cada saída mostre o mapa de Karnaugh e a indicação dos agrupamentos de bits obtidos, e o respectiva produto (implicante). 3) Para cada saída deve ser apresentada a expressão lógica minimizada e também o circuito lógico obtido. Os projetos serão depois implementados em hardware, quando você saberá se houve algum erro no seu projeto. A entrega será feita pessoalmente para o professor no prazo indicado no Moodle.

4.2 AE2 - Conhecendo os dispositivos lógicos programáveis

AE2 - Conhecendo os dispositivos lógicos programáveis

Objetivos Conhecer o Quartus Prime e as características dos dispositivos lógicos programáveis Analisar os tempos de propagação em um circuito combinacional Alterar configurações do compilador Fazer a simulação funcional de um circuito combinacional. Atividades PASSO 0: Abrindo o Quartus Prime na Nuvem do IFSC Abra um terminal na maquina local LINUX [CRTL]+[ALT]+T Acesso no IFSC via ssh Abra o Quartus Prime PASSO 1: Realize a atividade descrita em Conhecendo os dispositivos lógicos programáveis - QUARTUS PRIME Ao escolher a família de FPGAS, escolha inicialmente um dispositivo da família Max II. Anote o código desse dispositivo. Capture as telas solicitadas e depois utilize-as no relatório da atividade. Anote o tempo utilizado para cada uma das etapas do processo de compilação. Anote o número de elementos lógicos utilizados e o número de pinos utilizados, bem com o percentual em relação ao número total do dispositivo. Anote algum erro (Error) ou alertas (Warnings) que o Quartus II indicar no painel de mensagens [Messages] Ao final salve o projeto em um arquivo QAR (sugestão PJ1.QAR) PASSO 2: Repita a atividade descrita em Conhecendo os dispositivos lógicos programáveis - QUARTUS PRIME, trocando a família e dispositivo a ser usado na implementação. Escolha nesta vez um dispositivos da família Cyclone IV E ou Stratix II GX. Anote o código desse dispositivo. Observe as mudanças que ocorrem tanto no tipo de Elemento Lógico disponível, no Chip Planner, no Pin Planner, e no circuito dos pinos de I/O. Note que estes FPGAs também apresenta novos componentes, tais como: Memória, Multiplicadores, DSP, PLL, DLL, etc. Verifique se consegue encontra-los no leiaute mostrado no Chip Planner, e documente aqueles que encontrar. Compare os resultados obtidos nos procedimentos do PASSO 1 e PASSO 2. PASSO 3: Realize o procedimento descrito em Medição de tempos de propagação em circuitos combinacionais - Quartus Prime Ao escolher a família de FPGAS, escolha um dispositivo FPGA da família Cyclone IV E. Anote o código desse dispositivo. Se você está com o código da AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos escrito, use este código no lugar do código do cálculo da distância de Hamming Capture as telas mostradas no roteiro e depois utilize-as no relatório da atividade. Anote o tempo máximo de propagação entre as entradas e saídas. Anote o número de elementos lógicos utilizados e o número de pinos utilizados, bem com o percentual em relação ao número total do dispositivo. Experimente modificar as configurações do compilador, conforme mostrado em Configurando o compilador. Se desejar mude a semente inicial trocando o valor de [Seed: 1] Experimente inserir diferentes restrições de atraso máximo para o compilador, e analise o resultado obtido. Anote algum erro (Error) ou alertas (Warnings) que o Quartus II indicar no painel de mensagens [Messages] Ao final salve o projeto em um arquivo QAR (sugestão PJ2.QAR) PASSO 4: Realize a simulação funcional de: Cálculo da distância de Hamming (hamming_distance.vhd) ou Circuito conversor de binário para BCD (bin2bcd.vhd) Siga as passos indicados em Simulação Funcional usando o ModelSim. Capture as telas que mostram o circuito funcionando e depois utilize-as no relatório da atividade. Anote algum erro (Error) ou alertas (Warnings) que o Modelsim indicar no painel de mensagens [Messages] Ao final salve o projeto em um arquivo QAR (sugestão PJ3.QAR) Entregas Envie um arquivo QAR contendo todos os arquivos necessário para compilar cada um dos projetos. Envie um relatório em PDF, incluindo as imagens capturadas (inclua um título para cada figura) e escreva para cada imagem um texto comentando o que representa. O relatório também deve ter a identificação (autor, título, data) uma breve introdução e uma conclusão. A descrição dos procedimentos feita na página wiki não precisa incluída no relatório. Use preferencialmente o Overleaf para gerar o relatório. Mas o uso de MS-Word, Libreoffice e Google Docs também é permitida. A entrega será feita através do Moodle da disciplina. Observe o prazo de entrega.

4.3 AE3 - Programação do kit Mercurio IV

AE3 - Programação do kit Mercurio IV

Objetivos Apreender como programar um FPGA usando um kit de desenvolvimento Baseado na AE1 - Projeto de um conversor de binário para mostrador de 7 segmentos, implementar o projeto em VHDL. Descrever um circuito que você projetou em VHDL, implentá-lo e testá-lo. Fazer as adaptações necessárias para que o circuito projetado funcione no kit escolhido Testar o circuito, e anotar os resultados. Procedimento de laboratório Passo 1 - Descrevendo o hardware e fazendo a Análise e Síntese Abra o projeto do conversor de binário para mostrador de 7 segmentos (já simulado em aula anterior) Fazer a análise e síntese e corrigir eventuais erros. -- A bibliteca std e o pacote standard são autodeclarados, então as linhas abaixo podem ser comentadas com "--" --library std; --use std.standard.all; entity BCD2SSD is port ( -- Entradas ABCD do circuito eA, eB, eC, eD: in bit; -- Saidas para os leds do mostrador de 7 segmentos. Note que o nome a, b, .. g foi mudado para ssd_a, ssd_b, ... ssd_g pois o VHDL é insensível a caixa ssd_a, ssd_b, ssd_c, ssd_d, ssd_e, ssd_f, ssd_g : out bit ); end entity; architecture ifsc_v1 of BCD2SSD is begin -- descreva a expressão lógica obtida para cada uma das saídas; -- Por exemplo: se for a = A + C + (B'.D') + (B.D) ssd_a <= eA or eC or (not eB and not eD) or (eB and eD); ssd_g <= ; end architecture; Passo 2 - Configurando o dispositivo e os pinos a serem utilizados Veja os detalhes em Preparando para gravar o circuito lógico no FPGA. Após escolher o kit a ser usado no projeto, é necessário informar ao Quartus II a família e o dispositivo (device) que será utilizado para DE2-115 {Assignments > Device... > Device family (Family: [Cyclone IV E], Name filter: [EP4CE115F29C7] ) > [OK]} para MERCÚRIO IV {Assignments > Device... > Device family (Family: [Cyclone IV E], Name filter: [EP4CE30F23C7] ) > [OK]} Após selecionar o dispositivo faça uma nova [Analysis and Synthesis]. Para evitar que saídas de circuitos da placa sejam ligadas ao terra através do FPGA, defina como alta impedância o estado dos pinos não utilizados no projeto. {Assignments > Device... > Device and Pin Options... > Category: Unused Pins > Reserve all unused pins: [As input tri-stated] > [OK] > [OK]} Atribua os pinos conforme a necessidade do projeto. Uso do Pin Planner {Assignments > Pin Planner} no modo tabela. Digite o número do pino na coluna {Location}. Apenas posições válidas são aceitas. Abra a página com o resumo da pinagem do kit Pinagem dos dispositivos de entrada e saída do kit MERCURIO IV. Observe a tabela com a pinagem das chaves disponíveis neste kit. Signal Name FPGA Pin No. Description I/O Standard SW[0] PIN_Y22 Chave tipo Slide Switch 0 3.3V SW[1] PIN_W21 Chave tipo Slide Switch 1 3.3V SW[2] PIN_W22 Chave tipo Slide Switch 2 3.3V SW[3] PIN_V21 Chave tipo Slide Switch 3 3.3V Configurar como entrada os seguintes pinos: eA V21 eB W22 eC W21 eD Y22 Observe a tabela com a pinagem dos display (mostrador de sete segmentos) disponíveis neste kit. Signal Name FPGA Pin No. Description I/O Standard DISP0_D[0] PIN_V2 Segmento A - Display 0 3.3V DISP0_D[1] PIN_V1 Segmento B - Display 0 3.3V DISP0_D[2] PIN_U2 Segmento C - Display 0 3.3V DISP0_D[3] PIN_U1 Segmento D - Display 0 3.3V DISP0_D[4] PIN_Y2 Segmento E - Display 0 3.3V DISP0_D[5] PIN_Y1 Segmento F - Display 0 3.3V DISP0_D[6] PIN_W2 Segmento G - Display 0 3.3V Configure como saída do FPGA os seguintes pinos: ssd_a V2 ssd_b V1 ssd_c U2 ssd_d U1 ssd_e Y2 ssd_f Y1 ssd_g W2 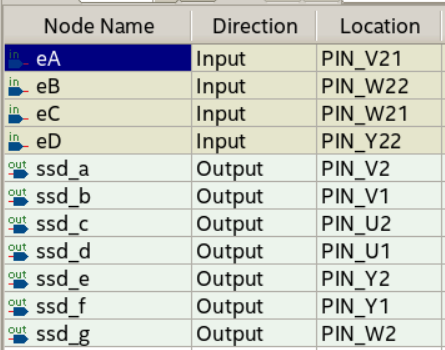A final do processo, o Pin Planner {Assignments > Pin Planner} deverá mostrar a correta pinagem conforme exemplificado na figura abaixo: Uma vez completada a configuração e pinagem, execute o Fitter (Place & Route). Após a compilação a mensagem de warning "Critical Warning (XXXXX): No exact pin location assignment(s) for XX pins of XX total pins" não deverá mais ser mostrada. Caso seja mostrada verifique qual o pino que não foi configurado corretamente e corrija. Passo 3 - Programando o FPGA Veja o procedimento de como deve ser feita a programação do FPGA em Programando o FPGA através da USB-Blaster Passo 4 - Testes de validação Realizar os seguintes testes, acionando as chaves A, B, C e D e observando o resultado no mstrador de sete segmentos: Carregar nas chaves os valores binários de 0 ("0000") a 9 ("1001") e observar se o valor mostrado é o desejado. Carregar nas chaves os valores binários de 10 ("1010") a 15 ("1111") e observar se o que é mostrado. Anote todos os resultados Digito ABCD ssd_a ssd_b ssd_c ssd_d ssd_e ssd_f ssd_g Mostrador 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 A 1010 B 1011 C 1100 D 1101 E 1110 F 1111 Relatório Técnico Documentar o experimento em um relatório técnico que contenha no mínimo: Identificação (título, disciplina, data, autores); Introdução; Descrição do procedimento realizado; Resultados obtidos (com imagens dos itens importantes) e análise dos resultados; Conclusão. Apêndice (se desejar pode ser disponibilizados vídeos do funcionamento do circuito no Passo 4 O relatório deve também responder as questões levantadas e mostrar que os objetivos apresentados na introdução foram atendidos.

5 Referências Bibliográficas:

Curso de Engenharia de Telecomunicações