PSD29007-Engtelecom(2019-2) - Prof. Marcos Moecke: mudanças entre as edições
Ir para navegação
Ir para pesquisar
| Linha 724: | Linha 724: | ||
pretty(vpa(H(z),3)) | pretty(vpa(H(z),3)) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
{{collapse bottom}} | |||
===Unidade 3=== | |||
{{collapse_top | expand=true | Unidade 3 - Filtros FIR}} | |||
;Aula 16 (23 set): | |||
*Filtros Digitais: Filtros FIR | |||
:*Filtros de fase linear: simétricos e antisimétricos (Tipo 1, 2, 3 e 4) | |||
:*Filtros de fase linear: propriedades (respostas em frequência possíveis, distribuição dos zeros em simetria quadrantal) | |||
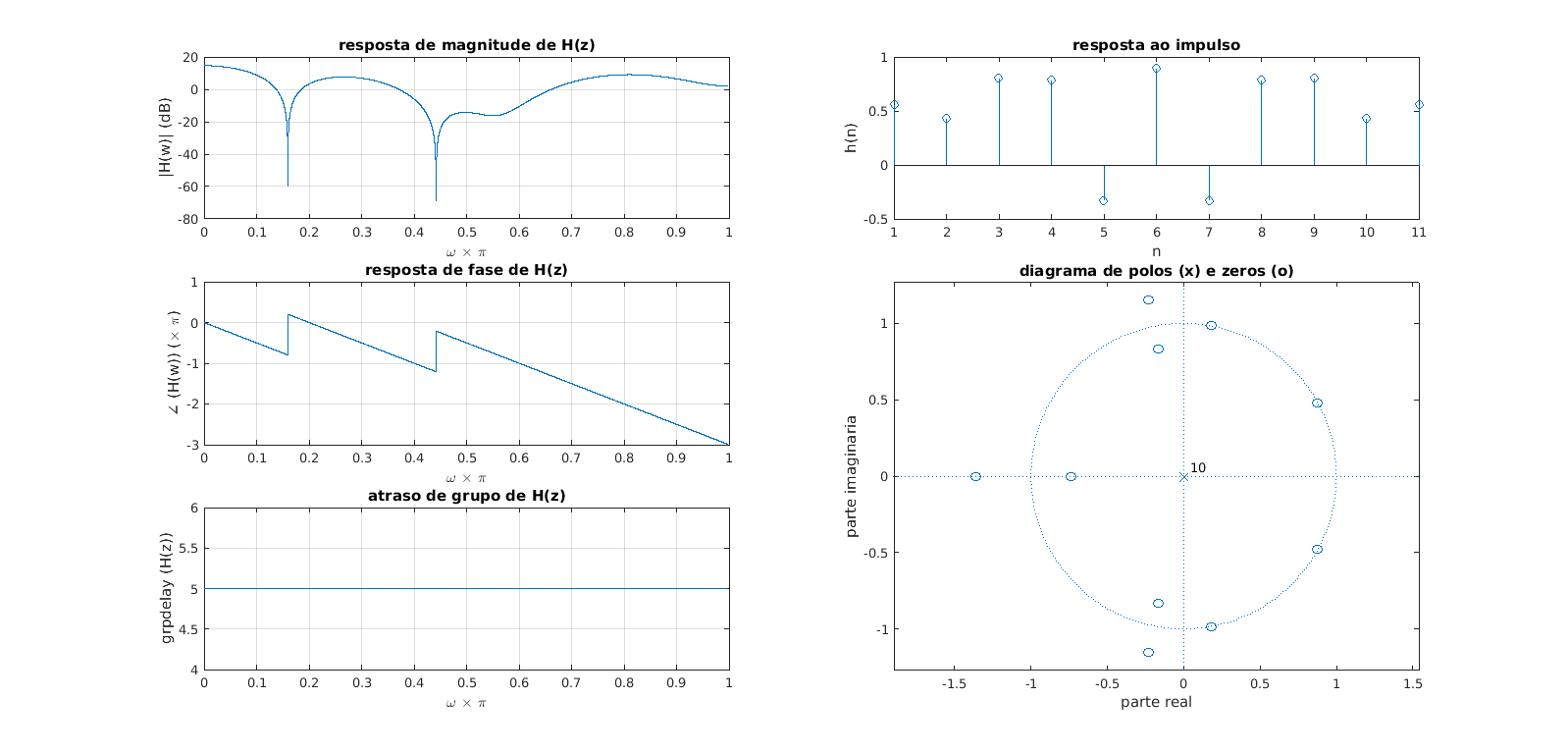
* Observar as propriedades dos FIR tipo 1, 2, 3 e 4. Observe a resposta de frequência, fase, atraso de grupo, coeficientes e diagrama de polos e zeros dos filtros abaixo. | |||
<syntaxhighlight lang=matlab> | |||
N = 10; | |||
bi = 2*(rand(1,N)-0.5) | |||
%% Tipo I - LP, HP, BS, BP | |||
b = [bi (2*rand(1,1)-0.5) flip(bi)]; | |||
... | |||
%% Tipo II - LP, BP | |||
% tem um zero em -1 | |||
b = [bi flip(bi)]; | |||
... | |||
%% Tipo III - BP | |||
% tem um zero em 1 e -1 | |||
b = [bi 0 -flip(bi)]; | |||
... | |||
%% Tipo IV - BP, HP | |||
% tem um zero em 1 | |||
b = [bi -flip(bi)]; | |||
... | |||
</syntaxhighlight> | |||
<center> | |||
[[Arquivo:FIR_tipo1.png | 800px]] | |||
<br> | |||
Figura 1 - Propriedades do filtro FIR de fase linear (Tipo 1) | |||
</center> | |||
<!-- | |||
;Aula 16 e 17 (19 e 24 abr) | |||
:*Coeficientes da série de Fourier de filtros ideias: LP, HP, BP, BS | |||
::*Passa-baixas (''Low-pass'') | |||
::<math>c_\text{LP}(n) = \left \{ \begin{matrix} \frac{\omega_c}{\pi}; & \qquad n = 0 \\ \frac {\sin (\omega_c n)}{\pi n}; & \qquad \left | n \right | > 0 \end{matrix}\right. </math> | |||
::*Passa-altas (''High-pass'') | |||
::<math>c_\text{HP}(n) = \left \{ \begin{matrix} 1-\frac{\omega_c}{\pi}; \qquad n = 0 \\ -\frac {\sin (\omega_c n)}{\pi n}; \qquad \left | n \right | > 0 \end{matrix}\right. </math> | |||
::*Passa-faixa (''Band-pass'') | |||
::<math>c_\text{BP}(n) = \left \{ \begin{matrix} \frac{\omega_{c2}-\omega_{c1}}{\pi}; \qquad n = 0 \\ \frac {\sin (\omega_{c2} n)- \sin (\omega_{c1} n)}{\pi n}; \qquad \left | n \right | > 0 \end{matrix}\right. </math> | |||
::*Rejeita-banda (''Band-stop'') | |||
::<math>c_\text{BS}(n) = \left \{ \begin{matrix} 1-\frac{\omega_{c2}-\omega_{c1}}{\pi}; \qquad n = 0 \\ -\frac {\sin (\omega_{c2} n)- \sin (\omega_{c1} n)}{\pi n}; \qquad \left | n \right | > 0 \end{matrix}\right. </math> | |||
:*Janela retangular, fenômeno de Gibbs | |||
:*Estudar no Matlab as funções [http://www.mathworks.com/help/signal/ref/wintool.html wintool], [http://www.mathworks.com/help/signal/ref/wvtool.html wvtool], [http://www.mathworks.com/help/signal/ref/window.html window] | |||
:*Ver pag. 249 a 256 de <ref name="SHENOI2006"/> | |||
:*Ver [https://www.mathworks.com/help/signal/ug/fir-filter-design.html FIR Filter Design] | |||
:*Uso de funções de janelamento temporal no projeto de filtros digitais. | |||
:*Tipos de janelas temporais usadas no projeto de filtros digitais. | |||
::*Retangular | |||
::<math>w(n)=1; \qquad -M \le n \le M </math> | |||
::*Bartlett | |||
::<math>w(n)= 1 - \frac{\left | n \right |}{M+1}; \qquad -M \le n \le M </math> | |||
::*Hanning | |||
::<math>w(n) = 0.5 + 0.5 \cos \left( \frac{2\pi n}{2M+1} \right), -M \le n \le M</math> | |||
::*Hamming | |||
::<math>w(n) = 0.54 + 0.46 \cos\left(\frac{2\pi n}{2M+1}\right); \qquad -M \le n \le M</math> | |||
::*Blackman | |||
::<math>w(n) = 0.42 + 0.5 \cos\left(\frac{2\pi n}{2M+1}\right) + 0.08\cos\left(\frac{4\pi n}{2M+1}\right); \qquad -M \le n \le M</math> | |||
* em todas as janelas <math>w\left ( n \right ) = 0 </math> quando <math> \left | n \right | \ge M</math> | |||
::onde <math>M </math> é <math>N/2</math> para <math>N</math> par e <math>(N+1)/2</math> para <math>N</math> impar | |||
*Uso de janelas fixas no Matlab : [http://www.mathworks.com/help/signal/ref/rectwin.html rect], [http://www.mathworks.com/help/signal/ref/triang.html triang], [http://www.mathworks.com/help/signal/ref/bartlett.html bartlett], [http://www.mathworks.com/help/signal/ref/hann.html hann], [http://www.mathworks.com/help/signal/ref/hamming.html hamming], [http://www.mathworks.com/help/signal/ref/blackman.html blackman], [http://www.mathworks.com/help/signal/ref/blackmanharris.html blackmanharris], [http://www.mathworks.com/help/signal/ref/nuttallwin.html nuttall]. | |||
::ver também [http://mathworld.wolfram.com/ApodizationFunction.html apodization function] | |||
<syntaxhighlight lang=matlab> | |||
L = 64; | |||
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L)); | |||
</syntaxhighlight> | |||
;Tabela 5.1: | |||
{| class="wikitable" border="1" cellpadding="3" cellspacing="0" style="text-align:center; font-size:100%" bgcolor="#efefef" | |||
! scope="col" width=25% align="center"| Janela | |||
! scope="col" width=10% align="center"| <math>A_{sl}</math> | |||
! scope="col" width=10% align="center"| <math>A_{s}</math> | |||
! scope="col" width=10% align="center"| <math>\Delta \omega</math> | |||
{{tabFIRwindow | Retangular | 13.3| 20.33 | 0.92<math>\pi</math>/M }} | |||
{{tabFIRwindow | Triangular | 26.6| 27.41 | }} | |||
{{tabFIRwindow | Bartlett | 26.5| 27.48 | }} | |||
{{tabFIRwindow | Hann | 31.5| 44.03 | 3.11<math>\pi</math>/M}} | |||
{{tabFIRwindow | Bartlett-Hanning | 35.9| 40.77| }} | |||
{{tabFIRwindow | Hamming | 42.5| 54.08 | 3.32<math>\pi</math>/M}} | |||
{{tabFIRwindow | Bohman | 46.0| 51.84 | 7.01<math>\pi</math>/M}} | |||
{{tabFIRwindow | Parzen | 53.1| 56.89 |}} | |||
{{tabFIRwindow | Blackman | 58.1| 75.25 | 5.56<math>\pi</math>/M}} | |||
{{tabFIRwindow | Flat Top | 88.0| 106.3| }} | |||
{{tabFIRwindow | Blackman-Harris | 92.1| 108.8 |}} | |||
{{tabFIRwindow | Nutfall | 93.8| 109.7|}} | |||
|} | |||
:*Dados acima obtidos para um filtro passa baixas de ordem N = 64 com <math>\omega_{c} = 0.5 \pi</math> | |||
:*Projeto de filtro FIR utilizando janelas temporais fixas. | |||
::* Exemplo de projeto | |||
Projetar um filtro passa baixas usando uma janela temporal fixa (verificar a janela que atende a especificação) | |||
wp = 0.2*pi; Ap = 0.2 dB; Gp = 0 dB | |||
ws = 0.3*pi; As = 60 dB; | |||
::* Informar qual o tipo de janela, a ordem obtida, e o valor de ''wc'' do projeto final | |||
::* Exemplo de projeto | |||
Projetar um filtro LP usando uma janela temporal fixa (hamming, bartlett-hanning, hanning). | |||
wp = 0.4*pi; Ap = 1 dB; Gp = 0 dB | |||
ws = 0.6*pi; As = 40 dB; | |||
::* Comparar os 3 tipos de janela, a ordem obtida, e o valor de ''wc'' em cada projeto. | |||
:: Use como uma estimativa inicial os valores da Tabela 5.1 pag. 268. | |||
::* PASSO 1 - Escolher o tipo de janela de acordo com a atenuação do lóbulo lateral Asl e As. | |||
::* PASSO 2 - Estimar a ordem N1 do filtro considerando os parâmetros Dw | |||
::* PASSO 3 - Calcule os coeficientes clp do filtro LP , calcule os valores da janela w e obtenha a resposta ao impulso do filtro h = clp * w. | |||
::* PASSO 4 - Ajuste o ganho do filtro para que a resposta na banda de passagem fique abaixo da especificação maxima. | |||
::* PASSO 5 - Verifique o valor real de Dwr = wAs-wAp, e faça a correção da ordem do filtro em função do desvio constatado. N2 = N*Dwr/Dw. | |||
::* PASSO 6 - Corrija o valor de projeto dos coeficientes Clp do filtro ideal, a janela e a resposta ao impulso. | |||
::* Repita o PASSO 3 até 6, até obter um filtro que atenda as especificações de Dw. | |||
::* PASSO 7 - Desloque a frequência de corte wc de modo a obter o valor correto de wp. wc2 = wp + (wp-wAp). | |||
:* Projeto de filtro FIR. | |||
::*Projete os dois filtros projetados anteriormente como IIR, utilizando 3 janelas diferentes. Compare os filtros obtidos com os filtros IIR. | |||
<syntaxhighlight lang=matlab> | |||
N = <ordem> | |||
h_fir = fir1(N,Wn,hamming(N+1)); | |||
[Hw,w] =freqz(h_fir); | |||
plot(w/pi,20*log10(abs(Hw))) | |||
title(['hamming N = ' num2str(N)]) | |||
%fvtool(h_fir,1) | |||
</syntaxhighlight> | |||
:*Ver pag. 256 a 265 de <ref name="SHENOI2006"/> | |||
:*Ver artigos: | |||
::*[https://ieeexplore-ieee-org.ez130.periodicos.capes.gov.br/stamp/stamp.jsp?tp=&arnumber=21693 A new window and comparison to standard windows] Yeong Ho Ha ; Pearce, J.A. IEEE Transactions on Acoustics, Speech, and Signal Processing, Feb. 1989, Vol.37(2), pp.298-301. | |||
::*[https://ieeexplore.ieee.org.ez130.periodicos.capes.gov.br/stamp/stamp.jsp?arnumber=1163506 Some windows with very good sidelobe behavior] Nuttall, A. IEEE Transactions on Acoustics, Speech, and Signal Processing, February 1981, Vol.29(1), pp.84-91 | |||
;Aula 19 a 21 (23 abr a 03 mai): | |||
*Filtros Digitais: Filtros FIR | |||
*Projeto de filtro FIR utilizando janelas temporais ajustáveis | |||
:*Uso de janelas ajustáveis no Matlab: [http://www.mathworks.com/help/signal/ref/kaiser.html kaiser], [http://www.mathworks.com/help/signal/ref/chebwin.html chebyshev], [http://www.mathworks.com/help/signal/ref/gausswin.html gauss], [http://www.mathworks.com/help/signal/ref/tukeywin.html tukey], [http://www.mathworks.com/help/signal/ref/taylorwin.html taylor]. | |||
<syntaxhighlight lang=matlab> | |||
L = 64; | |||
r = 60; % Chebyshev e Tukey | |||
alpha = 3; % Gauss | |||
betha = 8; % Kaiser | |||
nbar = 10; % Taylor | |||
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r)); | |||
</syntaxhighlight> | |||
Para a janela de Kaiser, a estimação do fator <math>\beta </math> e da ordem do filtro <math> N </math> são obtidos por: | |||
<math>\beta = \left \{ \begin{matrix} 0.1102 (\alpha-8.7), & \alpha > 50, \\ 0.5842 (\alpha- 21)^{0.4} + 0.07886 (\alpha- 21) , & 50 \ge \alpha \ge 21, \\ 0, & \alpha < 21. \end{matrix}\right.</math> | |||
<math> N = \frac {\alpha - 8} {2.285 \Delta \omega} + 1. </math> | |||
onde <math> \alpha </math> é a atenuação do lóbulo lateral e <math> \Delta \omega </math> é a largura da banda de transição em rad/amostra. | |||
A janela de Kaiser é definida por: | |||
<math> w(n) = \frac{I_0 \left(\beta \sqrt{1-(\frac{n-\alpha}{\alpha})^2} \right)}{I_0(\beta)} </math> | |||
onde :<math> I_0(x) = 1+ \sum_{k=1}^\infty {\left( \frac{(\frac{x}{2})^k}{k!}\right)}^2 </math> é a função de Bessel de ordem zero [http://mathworld.wolfram.com/ModifiedBesselFunctionoftheFirstKind.html] | |||
Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com <math> f_{pass} = 1000 Hz </math>, <math> f_{stop} = 1500 Hz </math>, <math> f_{amostragem} = 8000 Hz </math> atenuação de 40 dB na "stopband" | |||
<syntaxhighlight lang=matlab> | |||
fsamp = 8000; | |||
fcuts = [1000 1500]; | |||
mags = [1 0]; | |||
devs = [0.01 0.01]; | |||
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp); | |||
</syntaxhighlight> | |||
Com os parâmetros é possível projetar o filtro usando a função fir1, que utiliza o método da janela para o projeto do filtro. | |||
<syntaxhighlight lang=matlab> | |||
h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale'); | |||
[Hw,w] =freqz(h_fir); | |||
plot(w*fsamp/2/pi,20*log10(abs(Hw))) | |||
title(['Kaiser filter N = ' num2str(n)]) | |||
%fvtool(h_fir,1) | |||
</syntaxhighlight> | |||
:*Ver as funções [http://www.mathworks.com/help/signal/ref/fir1.html fir1], [http://www.mathworks.com/help/signal/ref/kaiserord.html kaiserord] do Matlab. | |||
:*Ver pag. 266 a 273 de <ref name="SHENOI2006"/> | |||
:* Uso das funções [http://www.mathworks.com/help/signal/ref/window.html window] e [http://www.mathworks.com/help/signal/ref/fir1.html fir1] do Matlab para projeto de filtro FIR | |||
<code> | |||
%% Exemplo de Filtro | |||
wp1 = 0.1 \pi; | |||
ws1 = 0.2 \pi; | |||
ws2 = 0.6 \pi; | |||
wp2 = 0.8 \pi; | |||
Ap = 1 dB; | |||
Ar = 40 dB; | |||
</syntaxhighlight> | |||
;Aula 22 (08 mai): | |||
*Filtros Digitais: Filtros FIR | |||
:*Filtro de Parks-McClellan. Funções [http://www.mathworks.com/help/signal/ref/firpm.html firpm] e [http://www.mathworks.com/help/signal/ref/firpmord.html firpmord]. | |||
:*[http://mathworld.wolfram.com/RemezAlgorithm.html Remez exchange algorithm] - o básico em Wolfram Alpha | |||
:*[http://eeweb.poly.edu/iselesni/EL713/remez/remez.pdf Remez exchange algorithm] - o detalhe com implementação em Matlab. Como resolver as anomalias na banda de transição. | |||
:*[http://www.ee.ic.ac.uk/hp/staff/dmb/courses/DSPDF/00700_OptimalFIR.pdf] | |||
*Projeto de filtro FIR | |||
:*projetar os filtros usando: 1) Janela fixa 2) Janela ajustável 3) Parks-McClellan. | |||
:*garantir que o filtro seja de menor ordem em cada caso, mas que esteja dentro das especificações. | |||
:*se necessário ajustar os valores de fs, fp, Ap, As, e a ordem do filtro, indicando o critério utilizado para o ajuste. | |||
<syntaxhighlight lang=matlab> | |||
%% Projetar o filtro passa baixas | |||
fp = 1200 Hz; | |||
fs = 1380 Hz; | |||
fa = 8000 Hz; | |||
Ap = 1 dB; | |||
Ar = 50 dB; | |||
</syntaxhighlight> | |||
<syntaxhighlight lang=matlab> | |||
%% Projetar o filtro passa altas | |||
fs = 1200 Hz; | |||
fp = 1380 Hz; | |||
fa = 8000 Hz; | |||
Ap = 1 dB; | |||
Ar = 50 dB; | |||
</syntaxhighlight> | |||
;Aula 23 (10 mai) | |||
*Projeto de filtro FIR | |||
:*projetar os filtros usando: 1) Janela fixa 2) Janela ajustável 3) Parks-McClellan. | |||
:*garantir que o filtro seja de menor ordem em cada caso, mas que esteja dentro das especificações. | |||
:*se necessário ajustar os valores de fs, fp, Ap, As, e a ordem do filtro, indicando o critério utilizado para o ajuste. | |||
<syntaxhighlight lang=matlab> | |||
%% Projetar o filtro passa faixa | |||
fs1 = 800 Hz; | |||
fp1 = 900 Hz; | |||
fp2 = 1000 Hz; | |||
fs2 = 1300 Hz; | |||
fa = 8000 Hz; | |||
Ap = 1 dB; | |||
Ar = 50 dB; | |||
</syntaxhighlight> | |||
<syntaxhighlight lang=matlab> | |||
%% Projetar o filtro rejeita faixa | |||
fp1 = 800 Hz; | |||
fs1 = 900 Hz; | |||
fs2 = 1000 Hz; | |||
fp2 = 1300 Hz; | |||
fa = 8000 Hz; | |||
Ap = 1 dB; | |||
Ar = 50 dB; | |||
</syntaxhighlight> | |||
Entrega do trabalho de projeto e análise de filtros digitais (05 de junho de 2019, as 9:40) | |||
<!-- | |||
;Aula 22 (09 out) | |||
:*Uso do [http://la.mathworks.com/help/dsp/ug/use-fdatool-with-dsp-system-toolbox-software.html] para projeto de filtro IIR, FIR equiripple e FIR com janela. | |||
*Uso do [http://la.mathworks.com/help/dsp/gs/design-and-implement-a-filter.html] no Simulink. | |||
;Aula 23 (23 out): | |||
:*Uso do Simulink | |||
::* Uso dos blocos de simulação [http://www.mathworks.com/help/simulink/slref/sinewave.html sinewave], [http://www.mathworks.com/help/simulink/slref/floatingscope.html scope] e [http://www.mathworks.com/help/dsp/ref/spectrumanalyzer.html Spectrum Analyzer]. | |||
::* Outros blocos [http://www.mathworks.com/help/simulink/slref/mux.html mux], [http://www.mathworks.com/help/simulink/slref/demux.html demux], [http://www.mathworks.com/help/simulink/slref/add.html sum], [http://www.mathworks.com/help/simulink/slref/product.html product]. | |||
::*[https://www.mathworks.com/help/simulink/gs/create-a-simple-model.html?s_cid=learn_doc Create Simple Model] [https://www.mathworks.com/videos/getting-started-with-simulink-118723.html] | |||
;Aula 24 (25 out): | |||
:*Uso do Simulink | |||
:*Tipos de Solver ([http://www.mathworks.com/help/simulink/ug/choosing-a-solver.html Choose a Solver]). | |||
:*Diferença entre processamento por amostra e processamento por quadro ([http://www.mathworks.com/help/dsp/ug/sample-and-frame-based-concepts.html Sample- and Frame-Based Concepts]). | |||
:*Exemplos: | |||
::*[https://www.mathworks.com/help/dsp/ug/filter-frames-of-a-noisy-sine-wave-signal-in-simulink.html Filtragem] - frame based | |||
::*[[Modulações Analógicas]] | |||
::*[[Amostragem de sinais]] | |||
::*[https://www.mathworks.com/help/dsp/ug/digital-filter-design-block.html Digital Filter Design Block], [https://www.mathworks.com/help/dsp/ref/digitalfilterdesign.html], [https://www.mathworks.com/help/dsp/ref/filterrealizationwizard.html] | |||
:::*É importante ler informações complementares sobre o [http://www.mathworks.com/help/simulink/gui/solver-pane.html Solver Pane], [http://www.mathworks.com/help/simbio/ug/simulating-models.html Model Simulation], [http://www.mathworks.com/help/simulink/ug/types-of-solvers.html Types of Solvers], [http://www.mathworks.com/help/simevents/ug/solvers-for-simevents-models.html Solvers for Discrete-Event Systems]. | |||
:::*É importante ler informações complementares sobre, [http://www.mathworks.com/help/simulink/sample-time.html Tempo de amostragem (Time Sample)], [http://www.mathworks.com/help/simulink/ug/how-to-view-sample-time-information.html View Sample Time Information], [http://www.mathworks.com/help/simulink/slref/concatenate.html Vector Concatenate, Matrix Concatenate] | |||
Para configurar o Simulink para sistemas discretos execute o comando dspstartup.m antes de abrir um novo modelo. | |||
;Aula 25 (ESTUDOS EXTRACLASSE): | |||
para compensar a palestra da MCC | |||
--> | |||
{{collapse bottom}} | {{collapse bottom}} | ||
Edição das 13h47min de 23 de setembro de 2019
1 Registro on-line das aulas
1.1 Unidade 1
| Unidade 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
1.1.1 Aula 1 EAD
Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz). %% Experimento 2.3 - Filtros Digitais
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
% FILE: Exp2_3.m
%% 1º filtro
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 ]'; P = [p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% 2º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p1 p1' p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% 3º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.99*exp(1j*pi/4);
p2 = 0.9*exp(1j*pi/4 - 1j*pi/30);
p3 = 0.9*exp(1j*pi/4 + 1j*pi/30);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p2 p2' p3 p3']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% Carregando o som
clear, close, clc
load handel;
%% Reproduzindo o som
sound(y,Fs)
% Reproduzindo o som
%soundsc(y,Fs)
% Reproduzindo o som
%player = audioplayer(y, Fs);
%play(player);
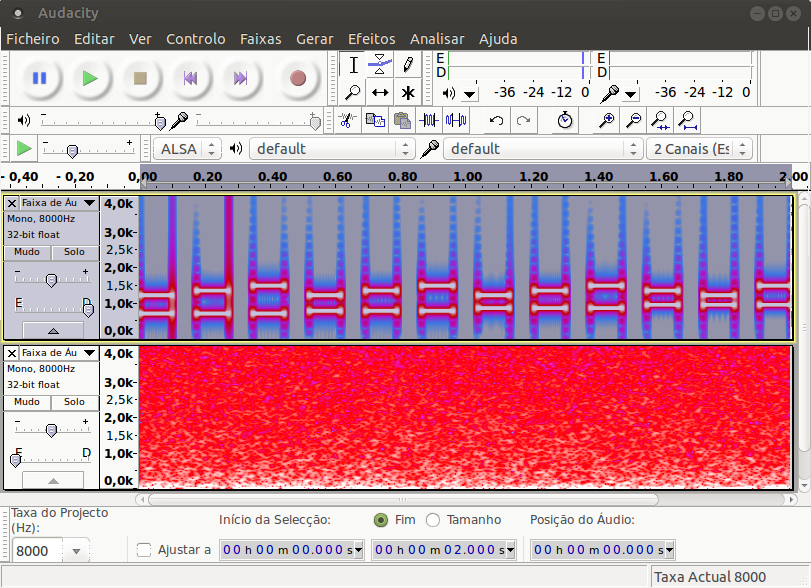
%% Carregando o som
clear, close, clc
[y,Fs] = audioread('DTMF_8kHz.ogg');
%% Reproduzindo o som
sound(y,Fs)
%% Visualizando o som no DT
time = [0:length(y)-1]'/Fs;
plot(time',y'); xlabel('segundos');
xlim([0 time(end)]), ylim([-1 1]);
%% Visualizando o som no DF
Nfreq = length(y);
freq = linspace(0,2*pi,Nfreq)'*Fs/pi/2;
Y = fft(y,Nfreq)/Nfreq;
plot(freq,abs(Y)); xlabel('Hertz');
xlim([0 Fs/2]);
|
1.2 Unidade 2
| Unidade 2 | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
b = [1 1];
a = [1 1 5];
[z1,p1,k]=tf2zp(b,a)
z2 = roots(b);
p2 = roots(a);
zplane(b,a);
%%
freqs(b,a);
%%
syms s w
H(s) = (s+1)/(s^2 + s + 5);
pretty(H(1j*w))
latex(H(1j*w))
%%
ws = logspace(-2, 1, 1000);
h = H(1j*ws);
subplot(211)
semilogx(ws,abs(h)); grid on;
subplot(212)
semilogx(ws,angle(h)/pi*180); grid on;
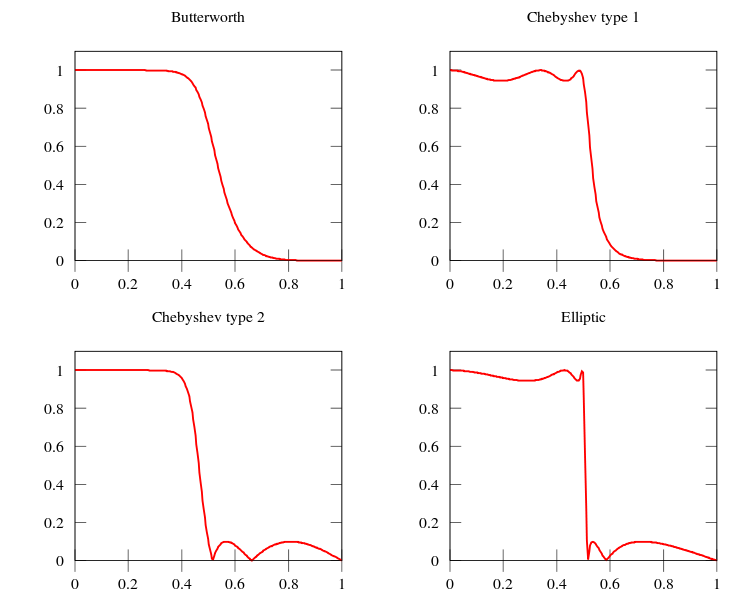
Os polinômios de Chebyshev de primeira ordem são definidos pela relação recursiva: Os primeiros cinco polinômios de Chebyshev de primeira ordem são:
%% Projeto de filtro passa-baixas usando funções do Matlab
%% Especificações do filtro
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');
%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');
%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');
%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');
fa = 200;
fN = fa/2;
wo = 60/fN; bw = 10/fN;
[b,a] = iirnotch(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000;
fN = fa/2;
wo = 941/fN; bw = 100/fN;
[b,a] = iirpeak(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000; fN = fa/2;
fo = 1000; bw = 20/fN;
[b,a] = iircomb(fa/fo,bw,'peak'); % ou use a flag 'notch'
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
|
1.3 Unidade 3
2 Avaliações
- Entrega dos diversas Atividades Extraclasse ao longo do semestre.
- Provas escritas A1 e A2
- Entrega do Projeto Final. O projeto é avaliado nos quesitos:
- 1) Implementação do Sistema,
- 2) Documentação,
- 3) Avaliação Global do aluno no projeto.
- Entrega dos Atividades Extraclasse ao longo do semestre AE1 a AE(N). A entrega, detalhes e prazos de cada AE serão indicados na plataforma Moodle
3 Referências Bibliográficas
- ↑ 1,0 1,1 1,2 1,3 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,0 2,1 2,2 2,3 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822