PSD29007-Engtelecom(2019-2) - Prof. Marcos Moecke
Ir para navegação
Ir para pesquisar
Registro on-line das aulas
Unidade 1
| Unidade 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Aula 1 EAD
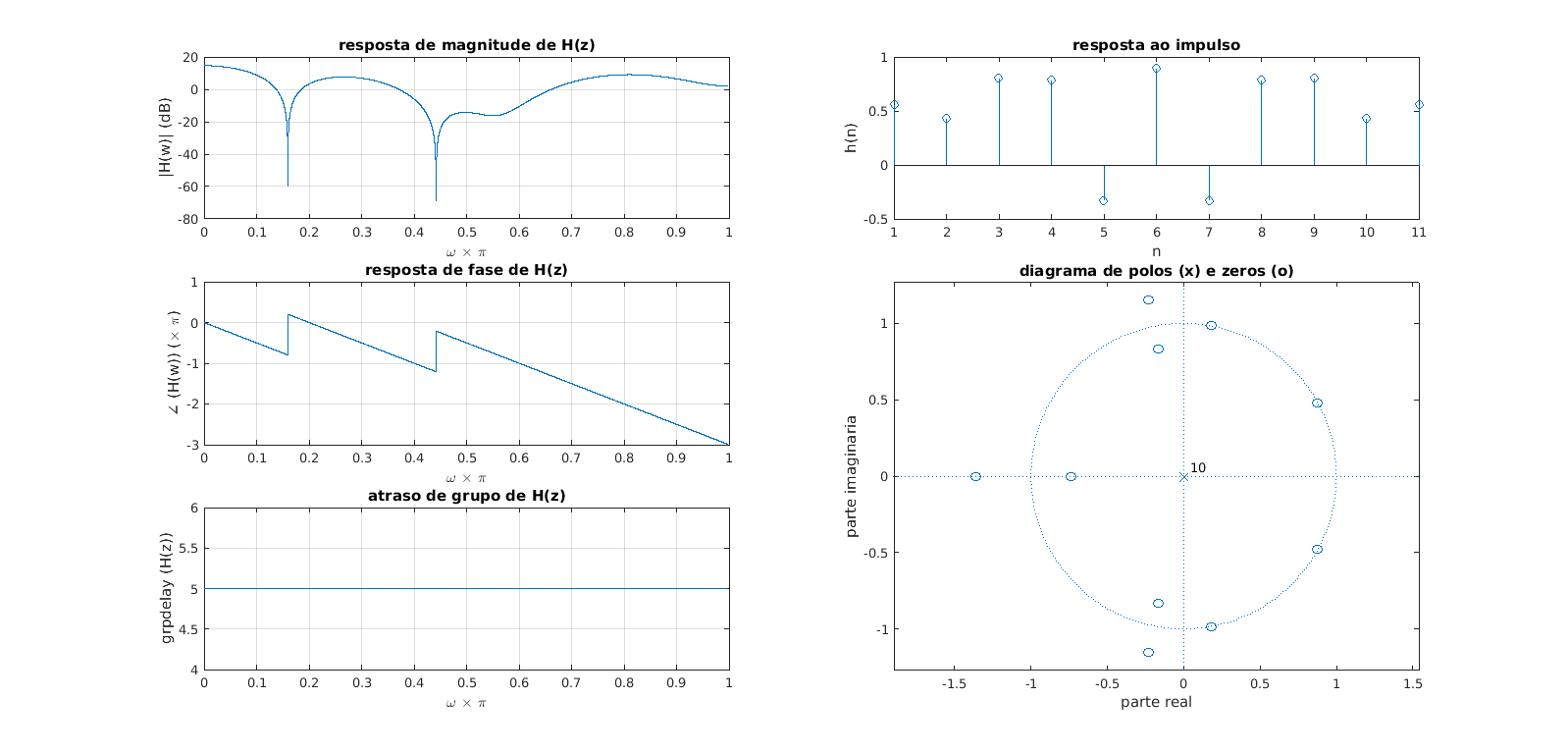
Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz). %% Experimento 2.3 - Filtros Digitais
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
% FILE: Exp2_3.m
%% 1º filtro
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 ]'; P = [p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% 2º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p1 p1' p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% 3º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.99*exp(1j*pi/4);
p2 = 0.9*exp(1j*pi/4 - 1j*pi/30);
p3 = 0.9*exp(1j*pi/4 + 1j*pi/30);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p2 p2' p3 p3']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
%% Carregando o som
clear, close, clc
load handel;
%% Reproduzindo o som
sound(y,Fs)
% Reproduzindo o som
%soundsc(y,Fs)
% Reproduzindo o som
%player = audioplayer(y, Fs);
%play(player);
%% Carregando o som
clear, close, clc
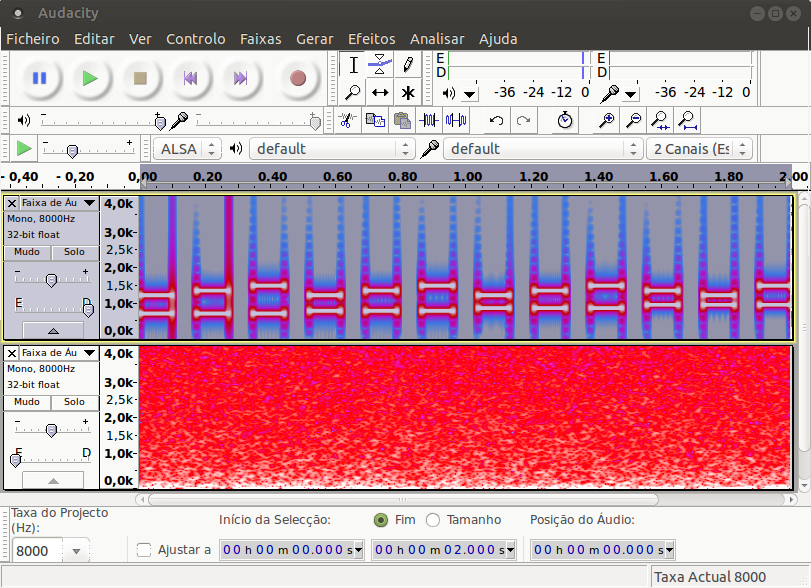
[y,Fs] = audioread('DTMF_8kHz.ogg');
%% Reproduzindo o som
sound(y,Fs)
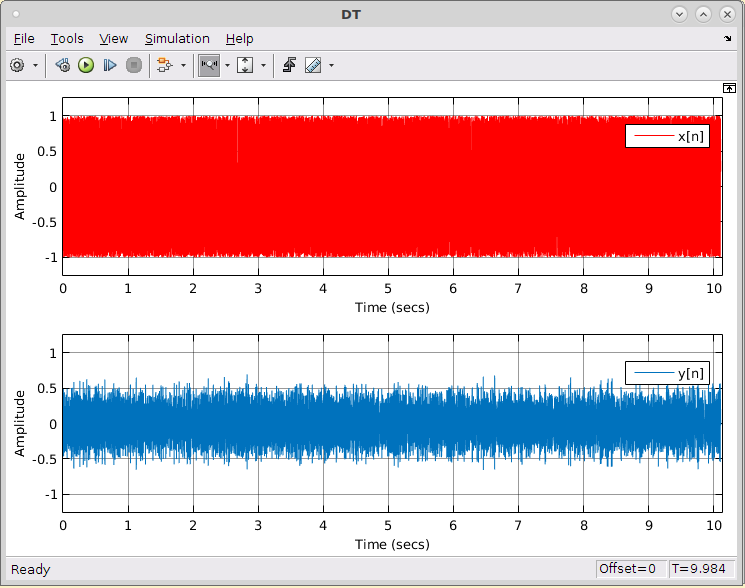
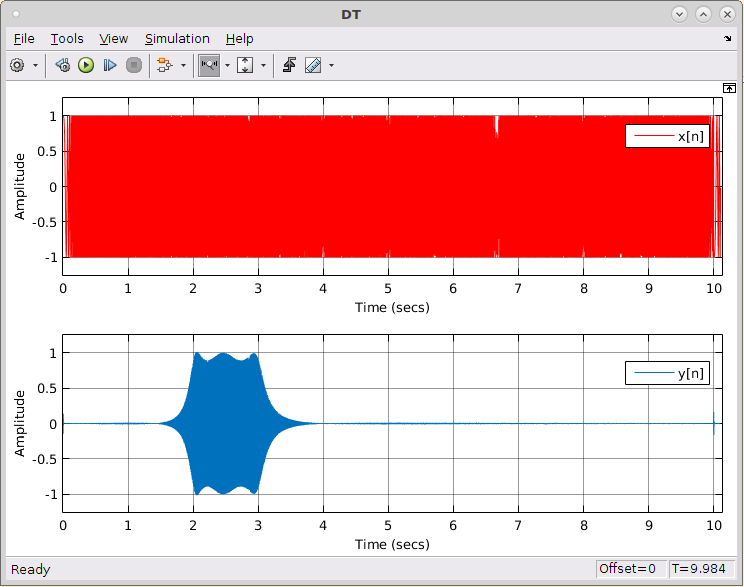
%% Visualizando o som no DT
time = [0:length(y)-1]'/Fs;
plot(time',y'); xlabel('segundos');
xlim([0 time(end)]), ylim([-1 1]);
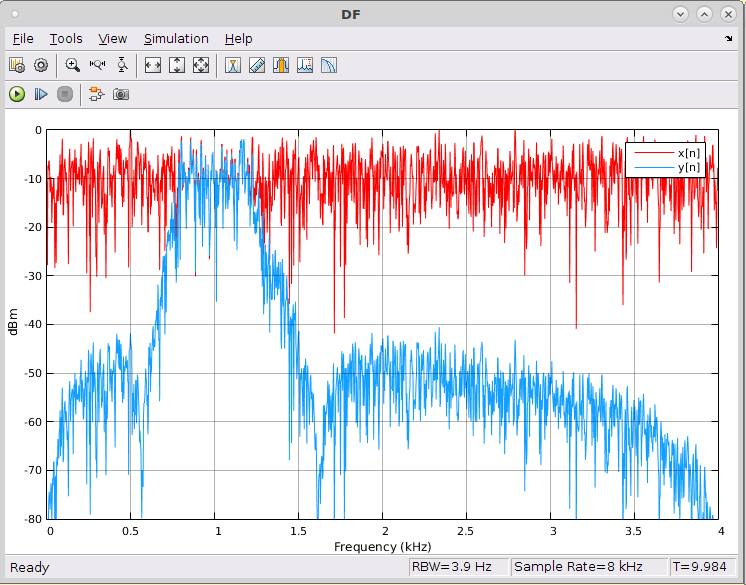
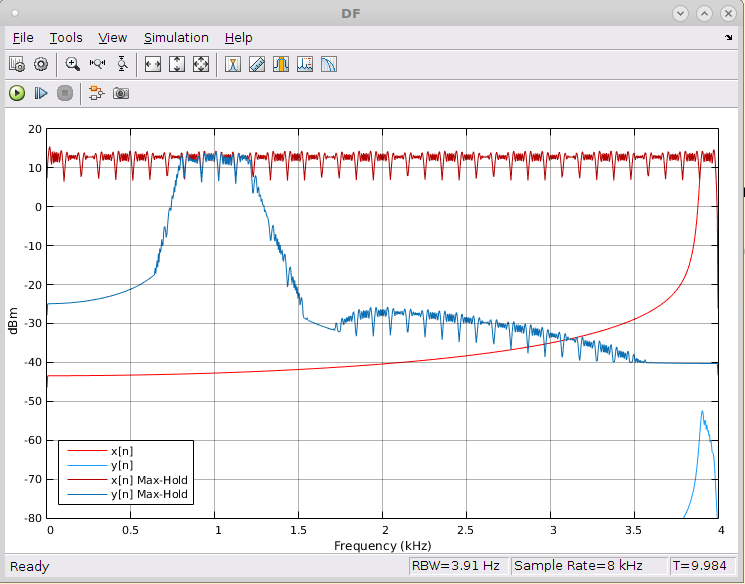
%% Visualizando o som no DF
Nfreq = length(y);
freq = linspace(0,2*pi,Nfreq)'*Fs/pi/2;
Y = fft(y,Nfreq)/Nfreq;
plot(freq,abs(Y)); xlabel('Hertz');
xlim([0 Fs/2]);
|
Unidade 2
| Unidade 2 | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
b = [1 1];
a = [1 1 5];
[z1,p1,k]=tf2zp(b,a)
z2 = roots(b);
p2 = roots(a);
zplane(b,a);
%%
freqs(b,a);
%%
syms s w
H(s) = (s+1)/(s^2 + s + 5);
pretty(H(1j*w))
latex(H(1j*w))
%%
ws = logspace(-2, 1, 1000);
h = H(1j*ws);
subplot(211)
semilogx(ws,abs(h)); grid on;
subplot(212)
semilogx(ws,angle(h)/pi*180); grid on;
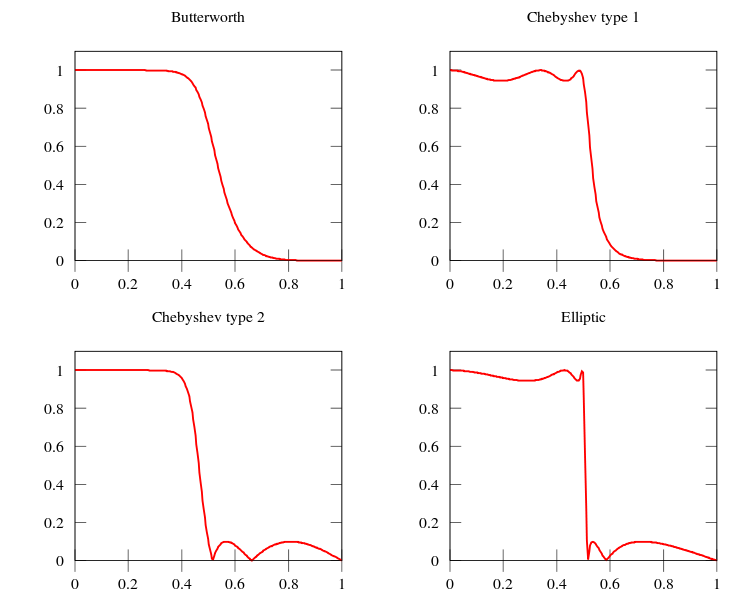
Os polinômios de Chebyshev de primeira ordem são definidos pela relação recursiva: Os primeiros cinco polinômios de Chebyshev de primeira ordem são:
%% Projeto de filtro passa-baixas usando funções do Matlab
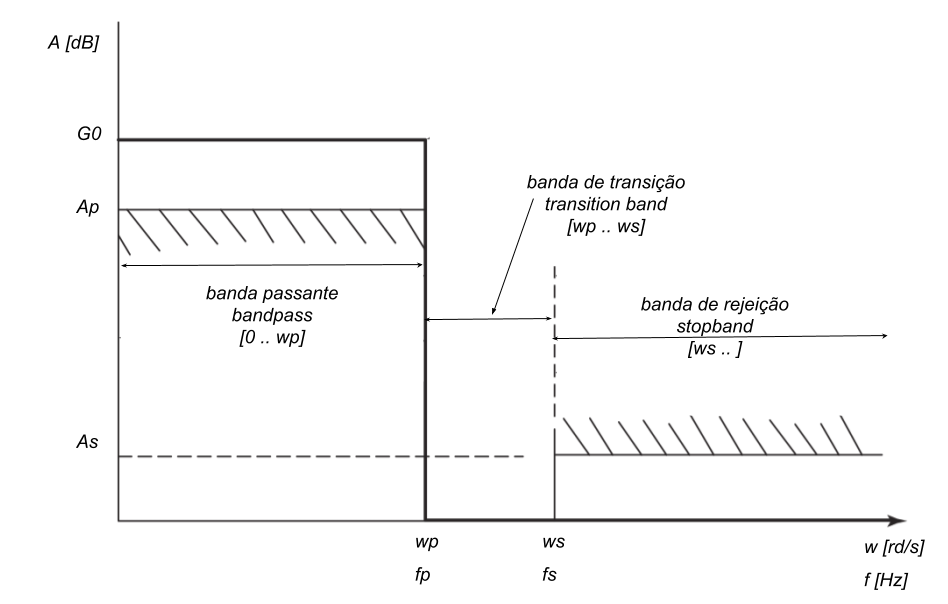
%% Especificações do filtro
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');
%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');
%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');
%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');
fa = 200;
fN = fa/2;
wo = 60/fN; bw = 10/fN;
[b,a] = iirnotch(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000;
fN = fa/2;
wo = 941/fN; bw = 100/fN;
[b,a] = iirpeak(wo,bw);
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
fa = 8000; fN = fa/2;
fo = 1000; bw = 20/fN;
[b,a] = iircomb(fa/fo,bw,'peak'); % ou use a flag 'notch'
fvtool(b,a);
syms z;
N(z) = poly2sym(b,z);
D(z) = poly2sym(a,z);
H(z) = N(z)/D(z);
pretty(vpa(H(z),3))
|
![{\displaystyle p_{k}=e^{\left[j{\frac {(2k+n-1)}{2n}}\pi \right]},k=1,2,3,...n}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e1e57e07651290d1e23c546bd09becd1e13dcc07)
![{\displaystyle n\geq {\frac {\log[(10^{0.1A_{s}}-1)/\epsilon ^{2}]}{2\log \Omega _{s}}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/baa878dd6bbe5a4d63ecda5c4e4dffe1e90e7ece)
![{\displaystyle p_{k}=\epsilon ^{(-1/n)}e^{\left[j{\frac {(2k+n-1)}{2n}}\pi \right]},k=1,2,3,...n}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0d089a7333523020d18a5fc153299ffe65966e6d)
Unidade 3
| Unidade 3 - Filtros FIR | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
N = 10;
bi = 2*(rand(1,N)-0.5)
%% Tipo I - LP, HP, BS, BP
b = [bi (2*rand(1,1)-0.5) flip(bi)];
...
%% Tipo II - LP, BP
% tem um zero em -1
b = [bi flip(bi)];
...
%% Tipo III - BP
% tem um zero em 1 e -1
b = [bi 0 -flip(bi)];
...
%% Tipo IV - BP, HP
% tem um zero em 1
b = [bi -flip(bi)];
...
L = 64;
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));
Projetar um filtro passa baixas usando uma janela temporal fixa (verificar a janela que atende a especificação) wp = 0.2*pi; Ap = 0.2 dB; Gp = 0 dB ws = 0.3*pi; As = 60 dB;
Projetar um filtro LP usando uma janela temporal fixa (hamming, bartlett-hanning, hanning). wp = 0.4*pi; Ap = 1 dB; Gp = 0 dB ws = 0.6*pi; As = 40 dB;
N = <ordem>
h_fir = fir1(N,Wn,hamming(N+1));
[Hw,w] =freqz(h_fir);
plot(w/pi,20*log10(abs(Hw)))
title(['hamming N = ' num2str(N)])
%fvtool(h_fir,1)
L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
Para a janela de Kaiser, a estimação do fator e da ordem do filtro são obtidos por:
onde é a atenuação do lóbulo lateral e é a largura da banda de transição em rad/amostra. A janela de Kaiser é definida por:
onde : é a função de Bessel de ordem zero [1] Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com , , atenuação de 40 dB na "stopband" fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.01 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
Com os parâmetros é possível projetar o filtro usando a função fir1, que utiliza o método da janela para o projeto do filtro. h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[Hw,w] =freqz(h_fir);
plot(w*fsamp/2/pi,20*log10(abs(Hw)))
title(['Kaiser filter N = ' num2str(n)])
%fvtool(h_fir,1)
Digital Filters with Linear Phase].
fa = 8000;
Ap = 0.4;
Ar = 40;
fp = 1000;
fr = 1500;
f = [fp fr];
a = [1 0];
dev = [(10^(Ap/20)-1)/(10^(Ap/20)+1) 10^(-Ar/20)];
[n,fo,ao,w] = firpmord(f,a,dev,fa);
b = firpm(n,fo,ao,w);
[h,w] = freqz(b,1,1024,fa);
plot(w, 20*log10(abs(h))); hold on;
plot([0 fr fr fa/2], [Ap/2 Ap/2 -Ar -Ar],':m')
plot([0 fp fp], [-Ap/2 -Ap/2 -(Ar+30)],':m');
ylim([-(Ar+30) Ap/2+10])
|
Unidade 4 - Realização de Filtros
| Unidade 4 - Realização de Filtros |
|---|
 
   
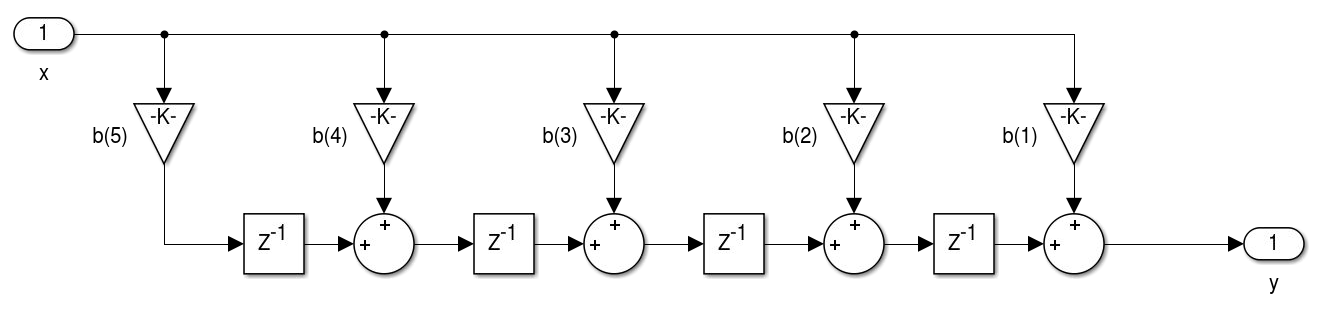
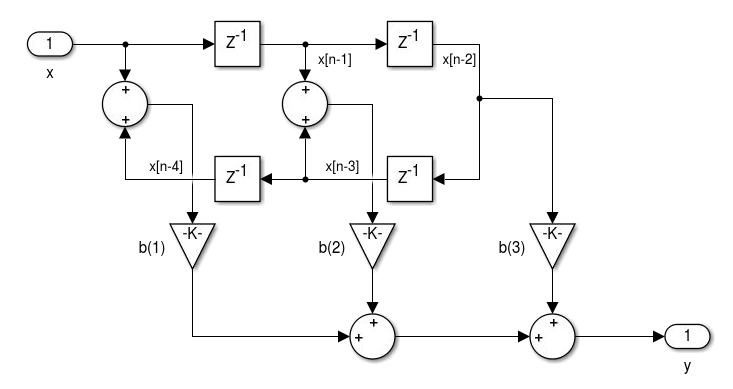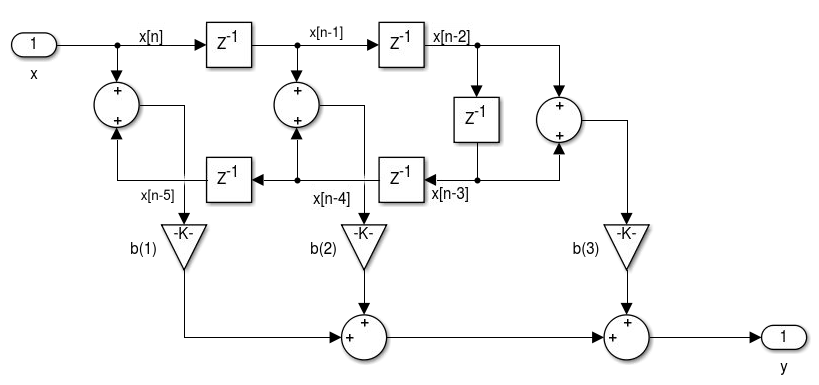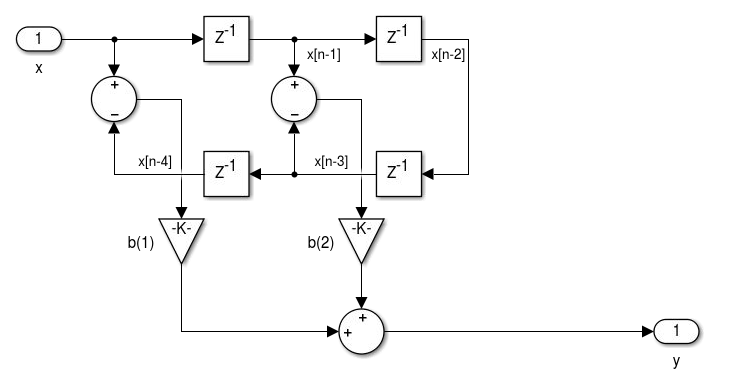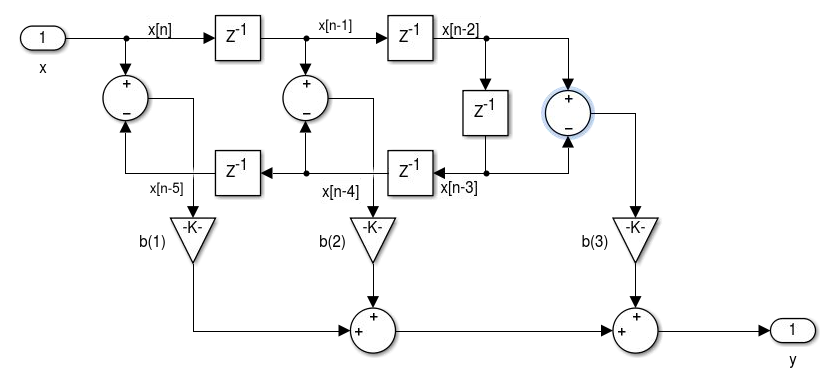
Fs = 30000; % Sampling Frequency
Fpass = 12000; % Passband Frequency
Fstop = 13000; % Stopband Frequency
Dpass = 0.01; % Passband Ripple
Dstop = 0.01; % Stopband Attenuation
flag = 'scale'; % Sampling Flag
% Calculate the order from the parameters using KAISERORD.
[N,Wn,BETA,TYPE] = kaiserord([Fpass Fstop]/(Fs/2), [1 0], [Dstop Dpass]);
% Calculate the coefficients using the FIR1 function.
b = fir1(N, Wn, TYPE, kaiser(N+1, BETA), flag);
hFIR = dsp.FIRFilter;
hFIR.Numerator = b;
% Para definir diretamente os coeficientes
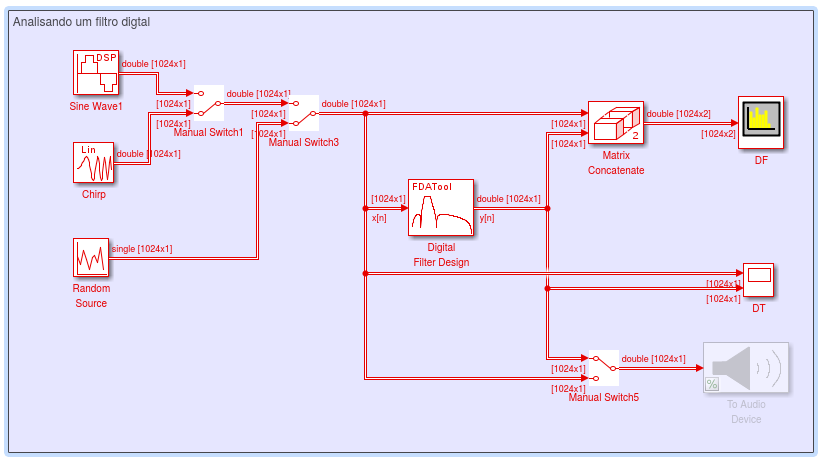
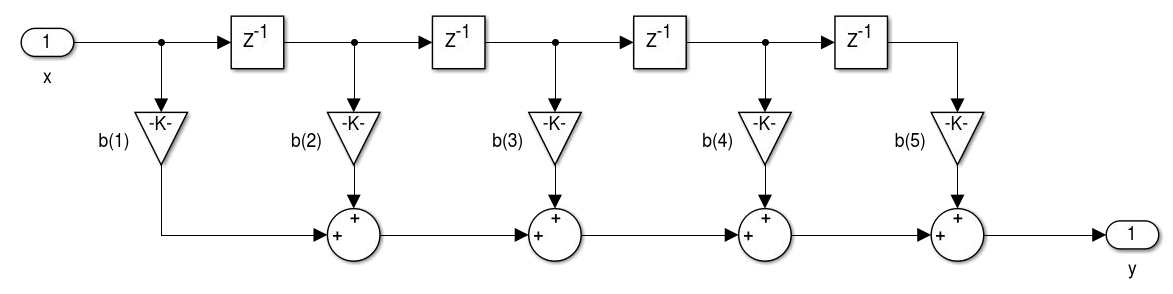
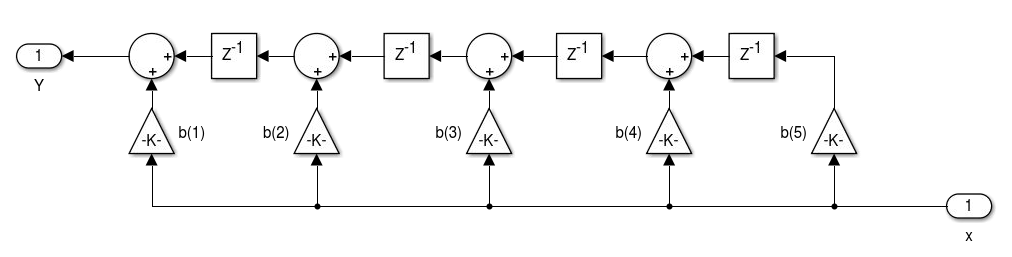
realizemdl(hFIR)
% Para definir os coeficientes através de uma matriz de entrada
realizemdl(hFIR,'MapCoeffsToPorts','on');
DICAS:
Para configurar o Simulink para sistemas discretos execute o comando dspstartup.m antes de abrir um novo modelo.
 
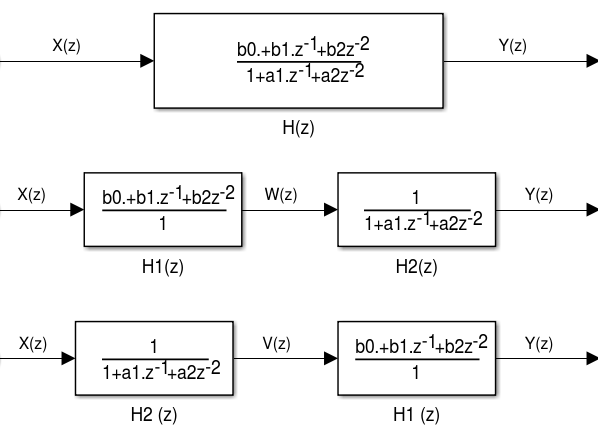
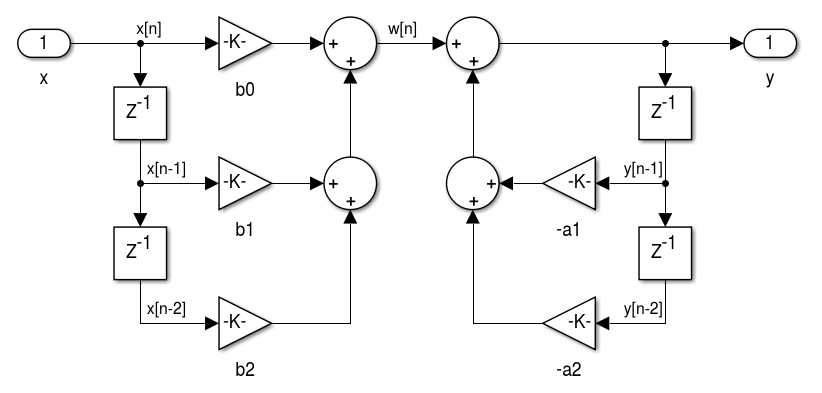
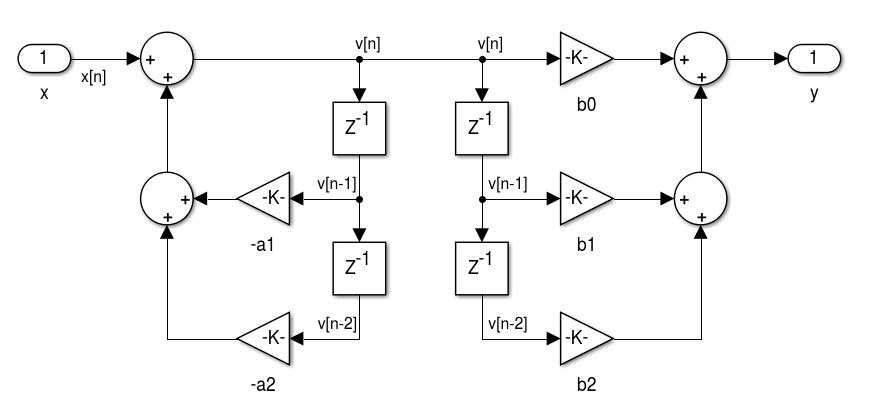
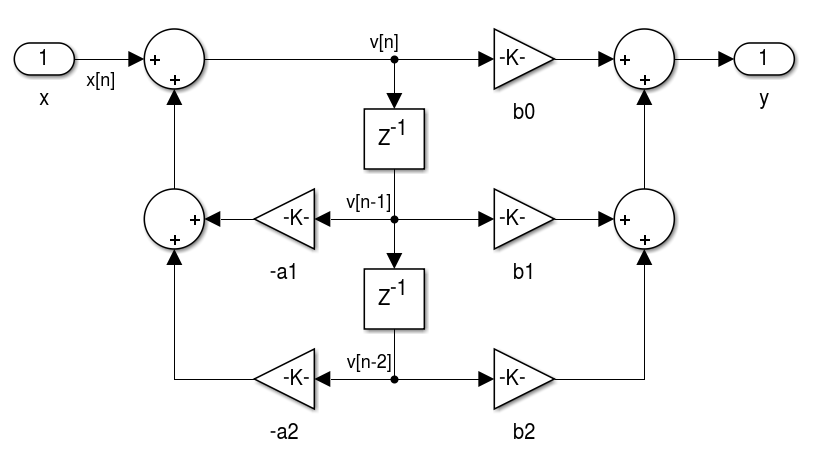
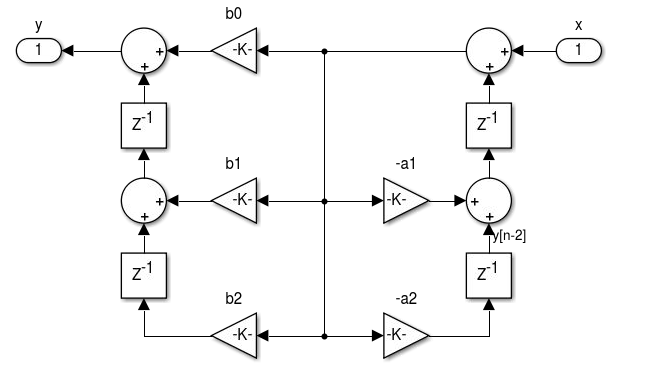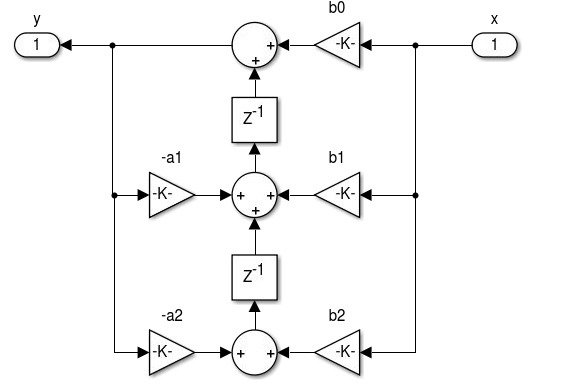
ATUAL
x=-0.2;
% Word length = 8, fraction length = 7
q=quantizer([8,7]);
xq=quantize(q,x);
binxq=num2bin(q,xq)
% Word length = 16, fraction length = 15
q1=quantizer([16 15]);
xq1 = quantize(q1,x);
binxq1=num2bin(q1,xq1)
|
Unidade 5 - Projeto Final
| Unidade 5 - Projeto Final | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Avaliações
Referências Bibliográficas
|
