PSD29007-Engtelecom(2020-1) - Prof. Marcos Moecke: mudanças entre as edições
| Linha 633: | Linha 633: | ||
:*Ver [[Uso do calculo simbólico na Matlab]] | :*Ver [[Uso do calculo simbólico na Matlab]] | ||
:*Ver pag. 186 a 204 de <ref name="SHENOI2006"> SHENOI, B. A. '''Introduction to Digital Signal Processing and Filter Design'''. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822 </ref> | :*Ver pag. 186 a 204 de <ref name="SHENOI2006"> SHENOI, B. A. '''Introduction to Digital Signal Processing and Filter Design'''. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822 </ref> | ||
;Aula 13 (6 abr): | ;Aula 13 (6 abr): | ||
| Linha 762: | Linha 761: | ||
*Plote o gráfico de <math> |Hp(p)| </math> e <math> |Hs(s)| </math>, indicando a máscara de especificação do filtro. | *Plote o gráfico de <math> |Hp(p)| </math> e <math> |Hs(s)| </math>, indicando a máscara de especificação do filtro. | ||
{{collapse bottom}} | {{collapse bottom}} | ||
====ATUAL==== | |||
;Aula 14 (9 abr): | |||
:* Uso das funções [http://www.mathworks.com/help/signal/ref/buttord.html buttord], [http://www.mathworks.com/help/signal/ref/butter.html butter], [http://www.mathworks.com/help/signal/ref/cheb1ord.html cheb1ord], [http://www.mathworks.com/help/signal/ref/cheby1.html cheby1], [http://www.mathworks.com/help/signal/ref/cheb2ord.html cheb2ord], [http://www.mathworks.com/help/signal/ref/cheby2.html cheby2], [http://www.mathworks.com/help/signal/ref/ellipord.html ellipord], [http://www.mathworks.com/help/signal/ref/ellip.html ellip] para o projeto de filtros analógicos com Matlab (é necessário usar o parâmetro ''''s''''). | :* Uso das funções [http://www.mathworks.com/help/signal/ref/buttord.html buttord], [http://www.mathworks.com/help/signal/ref/butter.html butter], [http://www.mathworks.com/help/signal/ref/cheb1ord.html cheb1ord], [http://www.mathworks.com/help/signal/ref/cheby1.html cheby1], [http://www.mathworks.com/help/signal/ref/cheb2ord.html cheb2ord], [http://www.mathworks.com/help/signal/ref/cheby2.html cheby2], [http://www.mathworks.com/help/signal/ref/ellipord.html ellipord], [http://www.mathworks.com/help/signal/ref/ellip.html ellip] para o projeto de filtros analógicos com Matlab (é necessário usar o parâmetro ''''s''''). | ||
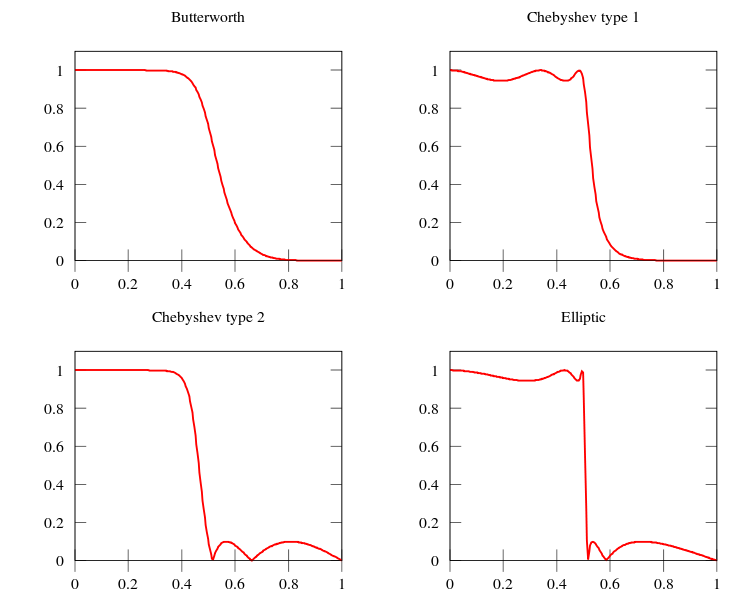
:* Ler '''Comparison of Analog IIR Lowpass Filters''' em [http://www.mathworks.com/help/signal/ref/ellip.html ellip] | :* Ler '''Comparison of Analog IIR Lowpass Filters''' em [http://www.mathworks.com/help/signal/ref/ellip.html ellip] | ||
| Linha 793: | Linha 795: | ||
:*Ver pag. 204 a 208 de <ref name="SHENOI2006"/> | :*Ver pag. 204 a 208 de <ref name="SHENOI2006"/> | ||
<!-- | |||
:* Uso das funções [http://www.mathworks.com/help/matlab/ref/semilogx.html semilogx], [http://www.mathworks.com/help/matlab/ref/semilogy.html semilogy],[http://www.mathworks.com/help/matlab/ref/logspace.html logspace], [http://www.mathworks.com/help/matlab/ref/linspace.html linspace]. | :* Uso das funções [http://www.mathworks.com/help/matlab/ref/semilogx.html semilogx], [http://www.mathworks.com/help/matlab/ref/semilogy.html semilogy],[http://www.mathworks.com/help/matlab/ref/logspace.html logspace], [http://www.mathworks.com/help/matlab/ref/linspace.html linspace]. | ||
:*Ver em [http://www.mathworks.com/help/signal/ug/iir-filter-design.html IIR Filter Design], [http://www.mathworks.com/help/signal/ug/special-topics-in-iir-filter-design.html Special Topics in IIR Filter Design]. | :*Ver em [http://www.mathworks.com/help/signal/ug/iir-filter-design.html IIR Filter Design], [http://www.mathworks.com/help/signal/ug/special-topics-in-iir-filter-design.html Special Topics in IIR Filter Design]. | ||
Edição das 23h20min de 8 de abril de 2020
1 Registro on-line das aulas
1.1 Unidade 1
| Unidade 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
profile on
profile viewer Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz).
|
1.2 Unidade 2
| Unidade 2 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Na sequência será mostrado como inicialmente projetar o filtro LP protótipo, e depois as transformações em frequência.
%%Definição do filtro
% Definindo os coeficientes do filtro
b = [1 1]; % Numerador
a = [1 1 5]; % Denominador
% Calculando os zeros (raízes do numerador) e pólos (raízes do denominador)
% Método 1 - usando a função tf2zp
[z1,p1,k]=tf2zp(b,a)
% Método 2 - obtendo as raízes
z2 = roots(b);
p2 = roots(a);
zplane(b,a);
%% Obtendo a resposta em frequência
% substitituindo a variável complexa s por jw usando a função freqz
freqs(b,a);
% Usando cálculo simbólico e plotando o gráfico com semilogx
syms s w
H(s) = (s+1)/(s^2 + s + 5);
pretty(H(1j*w))
latex(H(1j*w))
%%
ws = logspace(-2, 1, 1000);
h = H(1j*ws);
subplot(211)
plot(ws,abs(h)); grid on;
%semilogx(ws,abs(h)); grid on;
subplot(212)
plot(ws,angle(h)/pi*180); grid on;
%semilogx(ws,angle(h)/pi*180); grid on;
Os projetos de filtro Butterworth com função de transferência utilizam os polinômios de Butterworth mostrados na tabela a seguir:
1.2.1 INÌCIO DAS AULAS REMOTAS
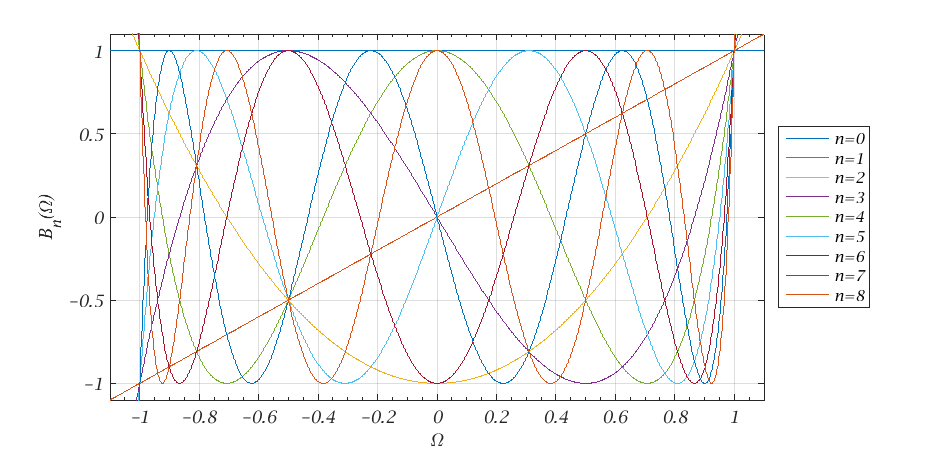
Para o projeto dos filtros do tipo Chebyshev, são utilizados os polinômios de Chebyshev de primeira ordem, os quais são definidos pela equação trigonométrica: Os dois primeiros polinômios são facilmente calculados como: O cálculo dos demais termos pode ser feita pela relação recursiva: Portanto o polinômio de grau 2 pode ser obtido por Assim os primeiros nove polinômios de Chebyshev de primeira ordem podem ser obtidos: Esses polinômios mostram um comportamento oscilatório entre . FONTE: Polinômios de Tchebychev, Wikipedia
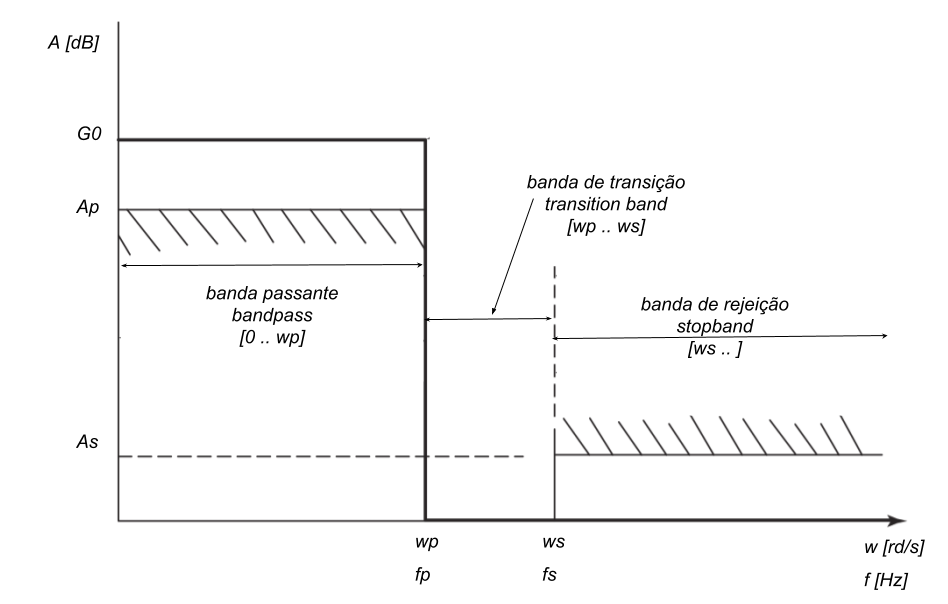
Para o projeto de filtros analógicos é necessário fazer as transformações de frequência indicadas abaixo, as quais devem ser consideradas no momento da determinação dos parâmetros do filtro protótipo LP.
1.2.2 ATUAL
%% Projeto de filtro passa-baixas usando funções do Matlab
%% Especificações do filtro
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');
%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');
%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');
%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');
|
2 Avaliações
- Atividades extraclasse
| AE1 - Cálculo de uma DFT de comprimento 8 |
|---|
|
| AE2 - Projeto de Filtros Analógico (Entrega e prazos ver Moodle) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Esta avaliação visa verificar se você conhece a metodologia de projeto de filtros analógicos: (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s), obtendo o filtro LP, HP, BP, BS, conforme o tipo de filtro desejado; Nesta avaliação é solicitado que cada equipe realize o projeto de 4 filtros.
|
- Prova escrita A1
- Entrega do Projeto Final. O projeto é avaliado nos quesitos:
- PFe - Documento de Especificação (apresentado no relatório);
- PFp - Implementação do Projeto;
- PFr - Relatório do Projeto (excluído a especificação);
- PFi - Avaliação individual do aluno no projeto (conceito subjetivo atribuído pelo professor a partir da observação e da apresentação do projeto).
3 Referências Bibliográficas
- ↑ 1,0 1,1 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,0 2,1 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822