PSD29007-Engtelecom(2020-1) - Prof. Marcos Moecke

1 Registro on-line das aulas

1.1 Unidade 1

Unidade 1

Aula 1 (10 fev) Apresentação da disciplina Auto inscrição na Plataforma Moodle de PSD29007 (engtelecom2020-1) Aula 2 (13 fev) Revisão de transformada de Laplace e Z Aula 3 e 4 (17 e 20 fev) Transformadas de Fourier Aula 5 (27 fev) Revisão de Sinais e Sistemas no tempo discreto em Matlab: Explorar a interface do Matlab. Funções de visualização das variáveis no workspace. Execução de instruções passo a passo. Escrita de script .m Uso da execução das seções de um script. Incremento de valor e execução. EXEMPLOS: Leia com atenção e execute o exemplo (Moving-Avarage Filter) na página de help da função filter. Revisão de Sinais e Sistemas no tempo discreto em Matlab: Leia com atenção o help Using FFT, abra o script clicando no botão [Open this Example]. Execute o script seção após seção. Note o uso da fft para determinar a frequência das manchas solares. Para melhorar o desempenho no Matlab recomendo que leiam a pagina do Help, . Também gostaria de lembra-los que a tecla F9 executa o código destacado no Help. Programação com scripts .m. Leia sobre manchas solares para entender o que são os dados do segundo exemplo. Sinais no dominio do tempo e dominio da frequencia. Uso da função fft Exemplo de uso da FFT %% Signal in Time Domain % Use Fourier transforms to find the frequency components of a signal buried in noise. % Specify the parameters of a signal with a sampling frequency of 1 kHz and a signal duration of 1.5 seconds Fs = 1000; % Sampling frequency T = 1/Fs; % Sampling period L = 1500; % Length of signal t = (0:L-1)*T; % Time vector % Form a signal containing a 50 Hz sinusoid of amplitude 0.7 and a 120 Hz sinusoid of amplitude 1. S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % Corrupt the signal with zero-mean white noise with a variance of 4. X = S + 2*randn(size(t)); % Plot the noisy signal in the time domain. It is difficult to identify the frequency components by looking at the signal X(t). subplot(311); plot(1000*t(1:200),X(1:200), 'b') title('Signal Corrupted with Zero-Mean Random Noise') xlabel('t (milliseconds)') ylabel('X(t)') hold on plot(1000*t(1:200),S(1:200),'r') hold off % Signal in Frequency Domain % Compute the Fourier transform of the signal. Y = fft(X); % Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1 based on P2 and the even-valued signal length L. P2 = abs(Y/L); P1 = P2(1:L/2+1); P1(2:end-1) = 2*P1(2:end-1); A2 = angle(Y); A1 = A2(1:L/2+1); % Define the frequency domain f and plot the single-sided amplitude spectrum P1. % The amplitudes are not exactly at 0.7 and 1, as expected, because of the added noise. % On average, longer signals produce better frequency approximations. f = Fs*(0:(L/2))/L; subplot(3,1,2); plot(f,P1, 'b') title('Single-Sided Amplitude Spectrum of X(t)') xlabel('f (Hz)') ylabel('|P1(f)|') hold on % Now, take the Fourier transform of the original, uncorrupted signal and retrieve the exact amplitudes, 0.7 and 1.0. Y = fft(S); P2 = abs(Y/L); P1 = P2(1:L/2+1); P1(2:end-1) = 2*P1(2:end-1); plot(f,P1, 'r') title('Single-Sided Amplitude Spectrum of S(t)') xlabel('f (Hz)') ylabel('|P1(f)|') hold off % Angulo / fase subplot(3,1,3); plot(f,A1) %ylim([0 1.05]) title('Single-Sided Phase Spectrum of X(t)') xlabel('f (Hz)') ylabel('phase(f)') Amostragem de Sinais (Experimento 1.2) Relembrar teorema da amostragem. Efeito da amostragem abaixo da frequência de Nyquist. Aliasing. Notar que as amostras de um sinal $s_1(t)=cos(2\pi \times 3t)$ (3 Hz) e um sinal $s_2(t)=cos(2\pi \times 7t)$ (7 Hz) são idênticas quando amostrado com um sinal de 10 Hz. Experimento 1.2 % Exemplos e Experimentos baseados no livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. %% Experimento 1.2 fs = 10; % frequencia (Hz) de amostragem dos sinais Ts = 1/fs; fase = 0; time = 0:Ts:(1-Ts); f1 = 3; % frequencia (Hz) do sinal s_1 f2 = 7; % frequencia (Hz) do sinal s_2 s_1 = cos(2*pi*f1*time+fase); s_2 = cos(2*pi*f2*time+fase); fsa = 1000; % frequência auxiliar de amostragem usada apenas para representação dos sinais originais Tsa = 1/fsa; time_aux = 0:Tsa:(1-Tsa); figure(1); stem(time,s_1,'ob'); hold on; plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k'); stem(time,s_2,'+r'); plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m'); hold off; legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo') DICAS: No help on-line da Mathworks, usando o botão [Try This Example > Try in your browser], permite executar o código no próprio browser sem ter nenhuma instalação do Matlab. Para verificar que o código realmente é executado mude a amplitude do ruído randômico para 0.1 ou 0.5, insira o comando close all antes da primeira linha, e execute todo o código [Run All] No help do Matlab, usando o botão [Open this Example], é possível executar o código seção a seção. Aula 7 (5 mar) Revisão de Sinais e Sistemas no tempo discreto em Matlab: Filtragem de Sinais (Experimentos 1.3, 2.1 e 2.2) Consulte a documentação do Matlab sobre roots, poly, linspace, logspace, residue, residuez, pretty, latex, freqs, freqz, syms, symfun, zplane. Ver também o Publish para a geração automática de relatórios em html, doc, pdf, latex ou ppt. Ver também Publishing MATLAB Code. Ver pag. 138 a 141 de Variação do Experimento 2.2 % Exemplos e Experimentos baseados no livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. %% Experimento 2.2 % Resposta em frequencia usando a função freqz N = 1; num = [1 0 0 0]; den = poly([0.8 0.2]) %den = [1 0.6 -0.16]; % modo 1 %[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]); %plot(w/pi, abs(H)); % modo 2 %[H,w]=freqz(num,den); %plot(w/pi, abs(H)); % modo 3 %[H,w]=freqz(num, den, 'whole'); %plot(w/pi, abs(H)); % modo 4 freqz(num, den, 'whole'); figure(2); zplane(num,den); %% Resposta em frequencia substituindo z -> e^(jw) syms z Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z); pretty(Hf) latex(Hf) N = 1; w = [0:pi/100:N*pi-pi/100]; plot(w/pi,abs(Hf(exp(1i*w)))) %title(['$' latex(Hf) '$'],'interpreter','latex') text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex') xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex') Verifique a diferença entre os tipos de plots comentados no código. substitua o denominador de H(z) por dois polos em [-0.8 -0.8]. verifique o que ocorre se forem utilizados polos complexos conjugados [0.3-0.4i 0.3+0.4i 0.1] verifique o que ocorre se forem utilizados polos complexos não conjugados [0.3-0.4i 0.3+0.8i] verifique o que ocorre se os polos estiverem fora do circulo unitário [1.2 -0.2]. Interprete este resultado Consulte a documentação do Matlab sobre zeros, ones, plot, stem, subplot, filter. Para usar melhor a interface do Matlab leia também Execução de seções e variação de valores nos scripts, e ainda Uso de gráficos no Matlab. Ver pag. 65 a 71 de Ver também PDF Documentation for MATLAB. Principalmente MATLAB Primer. 1.1.1 ATUAL Aula 8 (9 mar) A filtragem de sinais digitais pode ser realizada de diferentes formas: convolução (y = conv(x,h)), onde x(n) é o sinal de entrada e h(n) é a resposta ao impulso do filtro (sistema linear invariante no tempo), filtragem no domínio do tempo (y = a1.x(n)+ a2.x(n-1)+ .. ak.x(n-k)); no domínio da frequência (y = ifft(fft(x)fft(h)) Variação do Experimento 3.1 %% Variação do Experimento 3.1 do livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. % FILE: Ex3_1.m % Exemplificando as possiveis formas de realizar a filtragem de um sinal x(n) clc; clear all; close all; %% Definindo valores iniciais Nh = 10; Nx = 20; %Nh = 400; Nx = 10000; x = ones(1,Nx); % A resposta ao impulso de um sistema h(n) % no filtro FIR aos coeficientes b(n) = h(n) h = [1:Nh]; b = h; %% Filtrando o sinal e medindo tempos % OPÇÃO 1 - Filtragem utilizando a convolução % NOTE: length(y) = length(x) + length(h) -1 tic; % iniciar a contagem do tempo y1 = conv(x,h); t(1) = toc; % terminar a contagem e mostrar tempo no console % OPÇÃO 2 - filtragem utilizando a equação recursiva % NOTE: length(y) = length(x) tic; y2 = filter(b,1,x); t(2) = toc; % OPÇÃO 3 - filtragem utilizando a equação recursiva % aumentando o tamanho de x para que length(y3) = length(y1) x3 = [x zeros(1,length(h)-1)]; tic; y3 = filter(h,1,x3); t(3) = toc; length_y = length(x) + length(h) - 1; % OPÇÃO 4 - filtragem utilizando a FFT % a y = IFFT(FFT(x)*FFT(h)) tic; X = fft(x,length_y); H = fft(h,length_y); Y4 = X.*H; y4 = ifft(Y4); t(4) = toc; % OPÇÃO 5 - filtragem utilizando a função fftfilt % a y = IFFT(FFT(x)*FFT(h)) tic y5 = fftfilt(h,x3); t(5) = toc; disp('Comprimento do vetor de saída length(y)') disp([' ' num2str([length(y1) length(y2) length(y3) length(y4) length(y5)])]) disp('Tempo usado na filtragem em micro segundos') disp([' ' num2str(t*1e6) ' us']) %% Plotando o gráfico subplot(411);stem(y1); hold on; stem(y2,'xr'); stem(y3,'+m'); legend('y1', 'y2', 'y3') hold off subplot(412);stem(y1, 'ob');legend('y1') subplot(413);stem(y2, 'xr'); hold on; stem(zeros(size(y1)),'.w');hold off; legend('y2') subplot(414);stem(y3, '+m');legend('y3') Verificar as funções tic e toc Notar a diferença de tempo de processamento entre os processos de filtragem. A situação pode ser muito diferente conforme muda o tamanho do sinal e ordem do filtro (h(n)). Modifique a resposta ao impulso e o sinal de entrada modificando os valores das variáveis de tamanho: Nh = 10, 100, 1000; Nx = 20, 1000, 10000; Em função do sistema operacional e reserva de memória para as variáveis é importante desprezar a primeira medida de tempo. Realize 3 medidas de tempo para cada uma das 5 opções de filtragem, com pelo menos duas combinações de comprimento Nh e Nx. Verifique o tempo de processamento usando a instrução profile profile on Após ativar o profiler, execute o programa e veja o tempo total do script e de cada função chamada. profile viewer Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz). Variação do Experimento 2.3 %% Experimento 2.3 - Filtros Digitais % Exemplos e Experimentos baseados no livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. % FILE: Exp2_3.m %% 1º filtro p1 = 0.9*exp(1j*pi/4); Z = [1 -1 ]'; P = [p1 p1']'; [num,den] = zp2tf(Z,P,1); [h,w] = freqz(num,den); figure(1); plot(w,abs(h)/max(abs(h))); figure(2); zplane(num,den); %% 2º filtro z1 = exp(1j*pi/8); z2 = exp(1j*3*pi/8); p1 = 0.9*exp(1j*pi/4); Z = [1 -1 z1 z1' z2 z2']'; P = [p1 p1' p1 p1' p1 p1']'; [num,den] = zp2tf(Z,P,1); [h,w] = freqz(num,den); figure(1); plot(w,abs(h)/max(abs(h))); figure(2); zplane(num,den); %% 3º filtro z1 = exp(1j*pi/8); z2 = exp(1j*3*pi/8); p1 = 0.99*exp(1j*pi/4); p2 = 0.9*exp(1j*pi/4 - 1j*pi/30); p3 = 0.9*exp(1j*pi/4 + 1j*pi/30); Z = [1 -1 z1 z1' z2 z2']'; P = [p1 p1' p2 p2' p3 p3']'; [num,den] = zp2tf(Z,P,1); [h,w] = freqz(num,den); figure(1); plot(w,abs(h)/max(abs(h))); figure(2); zplane(num,den);

1.2 Unidade 2

Unidade 2

Aula 9 (12 mar) Conceitos Gerais sobre Filtros Analógicos Função de transferência $H(s)=\frac{c_0+c_{1}s+c_2{s}^2+...+c_m{s}^m}{d_0+d_{1}s+d_2{s}^2+...+d_n{s}^n},m\le n$ Resposta em frequência: para obter a resposta em frequência é necessário avaliar $H(j\omega )=H(s)|\begin{array}{c}\\ s=j\omega \end{array}$ $H(j\omega )=|H(j\omega )|e^{j\varphi (\omega )}$ ${|H(j\omega )|}^2=H(j\omega )H(-j\omega )$ $e^{j2\varphi (\omega )}=\frac{H(j\omega )}{H(-j\omega )}$ O projeto de filtros analógicos é realizado em 2 etapas: projeto de um filtro passa baixas (LP) protótipo normalizado $H(p)$ com frequência de passagem ${\mathrm{\Omega }}_s=1$ transformação em frequência para o tipo de filtro (LP, HP, BP ou BS) $H(s)=H(p)|\begin{array}{c}\\ p=g(s)\end{array}$ Na sequência será mostrado como inicialmente projetar o filtro LP protótipo, e depois as transformações em frequência. No entanto, antes de projetar filtros, vejamos a análise básica de filtros analógicos utilizando o Matlab. Dado um sistema linear invariante no tempo, representado pela função de transferência $H(s)$, obter a resposta de frequência do sistema (Magnitude e Fase). $H(s)=\frac{s+1}{s^2+s+5}$ $H(j\omega )=\frac{s+1}{s^2+s+5}|\begin{array}{c}\\ s=j\omega \end{array}$ $H(j\omega )=\frac{1+w\mathrm{i}}{-w^2+w\mathrm{i}+5}$ %%Definição do filtro % Definindo os coeficientes do filtro b = [1 1]; % Numerador a = [1 1 5]; % Denominador % Calculando os zeros (raízes do numerador) e pólos (raízes do denominador) % Método 1 - usando a função tf2zp [z1,p1,k]=tf2zp(b,a) % Método 2 - obtendo as raízes z2 = roots(b); p2 = roots(a); zplane(b,a); %% Obtendo a resposta em frequência % substitituindo a variável complexa s por jw usando a função freqz freqs(b,a); % Usando cálculo simbólico e plotando o gráfico com semilogx syms s w H(s) = (s+1)/(s^2 + s + 5); pretty(H(1j*w)) latex(H(1j*w)) %% ws = logspace(-2, 1, 1000); h = H(1j*ws); subplot(211) plot(ws,abs(h)); grid on; %semilogx(ws,abs(h)); grid on; subplot(212) plot(ws,angle(h)/pi*180); grid on; %semilogx(ws,angle(h)/pi*180); grid on; Para aproximação de magnitude de filtros analógicos o projeto pode usar as aproximações de Butterworth, Chebyshev (tipo 1 ou 2) ou Cauer, mostradas na figura abaixo. Projeto de filtros analógicos do tipo Butterworth Os projetos de filtro Butterworth com função de transferência $H_n(s)=1/B_n(s)$ utilizam os polinômios de Butterworth $B_n(s)$ mostrados na tabela a seguir: n Fatores Polinomiais de $B_n(s)$ 1 $(s+1)$ 2 $(s^2+1.4142s+1)$ 3 $(s+1)(s^2+s+1)$ 4 $(s^2+0.7654s+1)(s^2+1.8478s+1)$ 5 $(s+1)(s^2+0.6180s+1)(s^2+1.6180s+1)$ 6 $(s^2+0.5176s+1)(s^2+1.4142s+1)(s^2+1.9319s+1)$ 7 $(s+1)(s^2+0.4450s+1)(s^2+1.2470s+1)(s^2+1.8019s+1)$ 8 $(s^2+0.3902s+1)(s^2+1.1111s+1)(s^2+1.6629s+1)(s^2+1.9616s+1)$ 9 $(s+1)(s^2+0.3473s+1)(s^2+s+1)(s^2+1.5321s+1)(s^2+1.879s+1)$ 10 $(s^2+0.3129s+1)(s^2+0.9080s+1)(s^2+1.4142s+1)(s^2+1.7820s+1)(s^2+1.9754s+1)$ Proposta de exercício Use os polinômios de Butterworth com ordens de 1 a 10 mostrados na tabela abaixo para obter os filtros . Escolha uma ordem n (entre 5 e 10) Plote a resposta em frequência em escala log da amplitude (em dB) e da fase (em rad/pi). Qual é o ganho do filtro na banda passante? Qual é a frequência de corte (-3dB) do filtro. Qual é o salto de de fase que ocorre em algumas frequências? Qual é o fator de atenuação em dB/decada após a frequência de corte? Faça o diagrama de polos e zeros desse filtro. Procure observar o que ocorre com a posição dos polos do filtro. Calcule o valor do módulo dos pólos. Aula 10 (25 mar) Projeto de filtros analógicos LP protótipo Projeto de filtros analógicos passa baixas (low pass - LP) do tipo Butterworth, considerando: ${\omega }_p$ é a frequência de passagem, $A_p=3dB$ é a atenuação em dB na frequência de passagem, ${\omega }_s$ é a frequência de stopband, $A_s$ é a atenuação em dB na frequência de stopband. Escalando as frequências em relação a ${\omega }_p$, teremos que ${\mathrm{\Omega }}_s=\frac{{\omega }_s}{{\omega }_p}$, e ${\mathrm{\Omega }}_p=\frac{{\omega }_p}{{\omega }_p}=1$ são as frequências de passagem e stopband do filtro protótipo $H(p)$, que tem ganho unitário e frequência de passagem 1. Casos em que o ganho na banda de passagem é $A_p=3dB$ Considerando o caso de filtro Butterworth com frequência de passagem ${\mathrm{\Omega }}_p$ e frequência de stopband (rejeição) de ${\mathrm{\Omega }}_s$, com ganho unitário em $\mathrm{\Omega }=0$ Se considerarmos o caso particular em que na frequência de passagem o ganho (em escala linear) deve ser $G_p=1/\sqrt{2}=0,707$, que corresponde a um ganho (em escala log) $G_p=-3dB$, ou atenuação $A_p=3dB$. Obtemos o fator $ϵ=\sqrt{10^{0.1A_p}-1}$, como sendo $ϵ=1$. Esse fator no caso dos filtros com atenuação $A_p=3dB$, acaba desaparecendo das equação de projeto. Para atenuações diferentes de 3 dB, ele ajusta a magnitude dos pólos. 2 ATUAL Assim, para projetar o filtro é necessário: 1) determinar a ordem $n$ do filtro utilizando a equação: $n\ge \frac{\log (10^{0.1A_s}-1)}{2\log {\mathrm{\Omega }}_s}$ 2) e em seguida obter os polos do filtro: $p_k=e^{\left[j\frac{(2k+n-1)}{2n}\pi \right]},k=1,2,3,...n$ 3) Com os pólos $p_k$ botem-se o denominador $D(p)=\prod _{k=1}^n(p-p_k)$ da função de transferência do filtro. 4) E assim obtém-se a função de transferência do filtro protótipo $H(p)=\frac{1}{D(p)}$ 5) Para obter a função de transferência do filtro analógico LP é necessário fazer uma transformação de frequência $H(p)->H(s)$ $H(s)=H(p)|\begin{array}{c}\\ p=\frac{s}{{\omega }_p}\end{array}$ 6) Se o ganho na frequência $\omega =0$ não for unitário G0, é ainda necessário ajustar o ganho do filtro do fator de ganho. Considerando que o valor do Ganho G0 seja dado em dB, teremos que $20*log10(G_{0(linear)})=G_{0(dB)}$, ou seja $G_{0(linear)}=10^{G_{0(dB)}/20}$ Exemplo Filtro LP Butterworth Projete um filtro Butterworth LP com ganho em $\omega =0$ G_0= 5dB, frequência de passagem ${\omega }_p=1000rad/s$ com ganho no mínimo de $A_p=2dB$, frequência de rejeição de ${\omega }_s=5000rad/s$, na qual o ganho deve ser inferior a -25 dB. Dados de $Hs(s)$ ${\omega }_p=$ ${\omega }_s=$ $G_{0(dB)}=$ $G_{p(dB)}=$ $G_{s(dB)}=$ Especificações de $Hp(p)$ ${\mathrm{\Omega }}_p=$ ${\mathrm{\Omega }}_s=$ $A_{0(dB)}=$ $A_{p(dB)}=$ $A_{s(dB)}=$ Determinação de $Hp(p)$ $ϵ=$ $n=$ $p_k=$ $D(p)=$ $Hp(p)=$ Determinação de $Hs(s)$ substituindo $p=\frac{s}{{\omega }_p}$ e corrigindo o ganho em G0 $Hs(s)=$ Obtida a função de transferência $Hs(s)=N(s)/D(s)$ obtenha a resposta em frequência, substituindo $s=j*\omega$ Obtenha a resposta em frequência, para $\omega =0,{\omega }_p,{\omega }_s,10{\omega }_p$ Plote o gráfico de $|Hp(p)|$ e $|Hs(s)|$, indicando a máscara de especificação do filtro. Casos em que o ganho na banda de passagem é um valor $A_p$ qualquer Teremos $ϵ=\sqrt{10^{0.1A_p}-1}$ Para projetar o filtro é necessário: 1) determinar a ordem $n$ do filtro: $n\ge \frac{\log [(10^{0.1A_s}-1)/{ϵ}^2]}{2\log {\mathrm{\Omega }}_s}$ 2) obter os polos do filtro: $p_k={ϵ}^{(-1/n)}{e}^{\left[j\frac{(2k+n-1)}{2n}\pi \right]},k=1,2,3,...n$ 3) obter a função de transferência: $H(p)=\frac{k}{D(p)}$, onde $k=\prod _{k=1}^n(-p_k)={ϵ}^{-1}$ e $D(p)=\prod _{k=1}^n(p-p_k)$. NOTA: o valor $k$ também pode ser obtido a partir de $D(p)$, pois corresponde ao último termo do polinômio $D(end)$. 4) No caso de um filtro LP é necessário ainda obter a função de transferência do filtro especificado fazendo a transformação de frequência $H(p)->H(s)$ $H(s)=H(p)|\begin{array}{c}\\ p=\frac{s}{{\omega }_p}\end{array}$ Exemplo Filtro LP Butterworth Projete um filtro Butterworth LP com ganho em $\omega =0$ G_0= 0dB, frequência de passagem ${\omega }_p=1000rad/s$ com atenuação máxima de $A_p=0.5dB$, frequência de rejeição de ${\omega }_s=5000rad/s$ com atenuação mínima de $A_p=30dB$. Dados de $Hs(s)$ ${\omega }_p=$ ${\omega }_s=$ $G_{0(dB)}=$ $G_{p(dB)}=$ $G_{s(dB)}=$ Especificações de $Hp(p)$ ${\mathrm{\Omega }}_p=$ ${\mathrm{\Omega }}_s=$ $A_{0(dB)}=$ $A_{p(dB)}=$ $A_{s(dB)}=$ Determinação de $Hp(p)$ $ϵ=$ $n=$ $p_k=$ $D(p)=$ $Hp(p)=$ Determinação de $Hs(s)$ substituindo $p=\frac{s}{{\omega }_p}$ e corrigindo o ganho em G0 $Hs(s)=$ Obtida a função de transferência $Hs(s)=N(s)/D(s)$ obtenha a resposta em frequência, substituindo $s=j*\omega$ Obtenha a resposta em frequência, para $\omega =0,{\omega }_p,{\omega }_s,10{\omega }_p$ Plote o gráfico de $|Hp(p)|$ e $|Hs(s)|$, indicando a máscara de especificação do filtro. Ver Uso do calculo simbólico na Matlab Ver pag. 186 a 204 de

3 Avaliações

• Atividades extraclasse

AE1 - Cálculo de uma DFT de comprimento 8

AE1 - Cálculo de uma DFT de comprimento 8. Determine a transformada discreta de Fourier X(w) a partir da sequencia discreta x(n) indicada na tabela abaixo. Utilize a equação da DFT $\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{0}}^{\mathrm{N}\mathrm{-}\mathrm{1}}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{W}_{\mathrm{N}}^{\mathrm{k}\mathrm{n}}$ ${\mathrm{W}}_{\mathrm{N}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{2}\mathrm{\pi }/\mathrm{N}}$ O algoritmo FFT indicado na tabela, onde dt é decimação no tempo (Fig 3.9) e df é decimação na frequência (Fig 3.13) Use uma folha de papel para anotar os valores dos produtos intermediários tanto da DFT como da FFT. Compare os resultados obtidos para de X(k) obtido com os dois cálculos. Poste no Moodle a folha de cálculos (digitalize usando scanner ou smartphone).

AE2 - Projeto de Filtros Analógico Butterworth (Entrega e prazos ver Moodle)

Esta avaliação visa verificar se você conhece a metodologia de projeto de filtros analógicos: (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s), obtendo o filtro LP, HP, BP, BS, conforme o tipo de filtro desejado; Nesta avaliação é solicitado que cada equipe realize o projeto de 4 filtros. Equipe Filtro 1 Filtro 2 Filtro 3 Filtro 4 Equipe 1 LP - (f1 = 200 Hz; f2 = 1000 Hz, Ap = 3 dB, As = 30 dB, G_p= 10 dB, Butterworth) HP - (f1 = Hz; f2 = Hz, Ap = dB, As = dB, G_p = dB) BP1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) BS1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) Equipe 2 LP - (f1 = 40 Hz; f2 = 200 Hz, Ap = 3 dB, As = 20 dB, G_p = 5 dB, Butterworth) HP - (f1 = Hz; f2 = Hz, Ap = dB, As = dB, G_p = dB) BP1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) BS1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) Equipe 3 LP - (f1 = 20 Hz; f2 = 100 Hz, Ap = 3 dB, As = 25 dB, G_p = 1 dB, Butterworth) HP - (f1 = Hz; f2 = Hz, Ap = dB, As = dB, G_p = dB) BP1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) BS1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) Equipe 4 LP - (f1 = 10 Hz; f2 = 60 Hz, Ap = 3 dB, As = 35 dB, G_p = -5 dB, Butterworth) HP - (f1 = Hz; f2 = Hz, Ap = dB, As = dB, G_p = dB) BP1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) BS1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) Equipe 5 LP - (f1 = 100 Hz; f2 = 500 Hz, Ap = 3 dB, As = 40 dB, G_p = -10 dB, Butterworth) HP - (f1 = Hz; f2 = Hz, Ap = dB, As = dB, G_p = dB) BP1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) BS1 - (f1 = Hz; f2 = Hz, f3 = Hz; f4 = Hz, Ap = dB, As = dB, G_p = dB) onde: LP (Low Pass)- Passa Baixa, HP (High Pass)- Passa Altas, BP (Band Pass)- Passa Faixa, BS (Band Stop)- Rejeita Faixa $f_N$ - são as "N" frequência de especificação do filtro dadas em Hertz (kHz ou MHz); Para LP $f_p=f_1$ e $f_s=f_2$. Para HP $f_s=f_1$ e $f_p=f_2$. Para BP $f_{s1}=f_1$ e $f_{p1}=f_2$, $f_{p2}=f_3$ e $f_{s2}=f_4$. Para BS $f_{p1}=f_1$ e $f_{s1}=f_2$, $f_{s2}=f_3$ e $f_{p2}=f_4$. 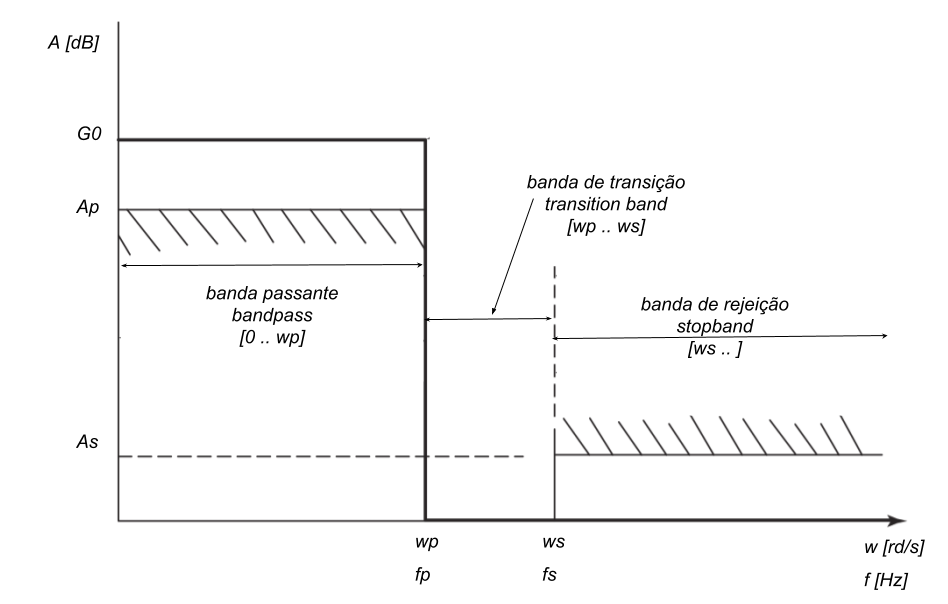$f_p$ - frequência de passagem; $f_s$ - frequência de rejeição (stopband), $A_p$ - Atenuação máxima na banda de passagem (dB), $A_s$ - Atenuação mínima na banda de rejeição (dB) (stopband), $G_p$ - Ganho médio na banda de passagem (dB). 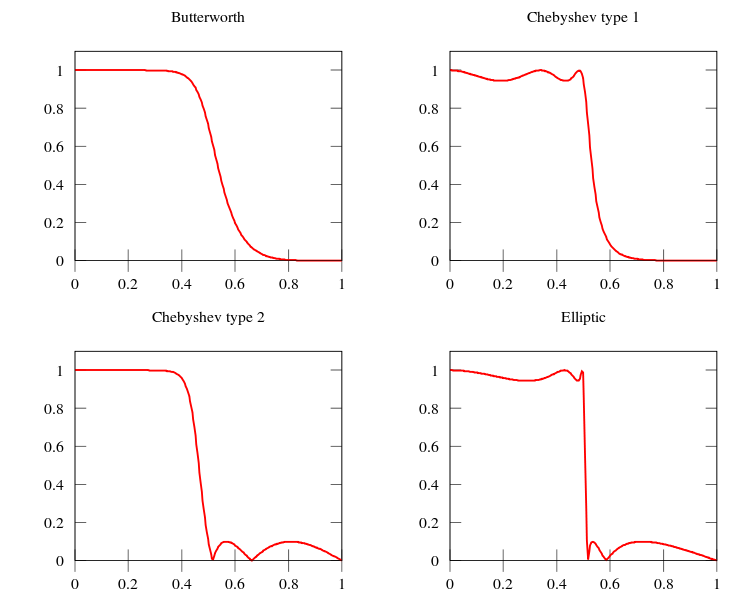Os filtros LP e HP devem ser realizados utilizando a aproximação de Butterworth ou Chebyshev tipo 1 (devendo ser todos os calculados efetuados a partir das equações). Os filtros BP e BS devem ser realizados utilizando a aproximação de Chebyshev tipo 2 ou Euler (podendo ser calculada a função H(p) a partir das funções do Matlab. A tabela acima indica o tipo de filtro que cada equipe deve utilizar. Para todos os filtros deve ser indicada a ordem do filtro, o valor de polos e zeros, e as equações de H(p), H(s). Deve ser apresentado de forma gráfica a resposta em frequência dos filtros (ganho em dB e fase) dos filtros (a) protótipo H(p), (b) Filtro analógico H(s). Utilize uma mascara com as especificações para mostrar que os filtros atendem a especificação original. Apresente o diagrama dos pólos e zeros dos filtros H(p), H(s). Utilize a mesma escala em dB para os gráficos de cada filtro. Nas abcissas utilize uma escala em Hz (kHz ou MHz). Utilize uma mascara com cor diferenciada para indicar claramente a especificação do filtro, e crie um segundo gráfico mostrando claramente a banda de passagem. Escreva um relatório técnico em PDF mostrando os resultados obtidos e comentando os resultados obtidos. Não é necessário apresentar a teoria utilizado para o projeto, mas todos os cálculos devem estar documentados. Envie o relatório em pdf ou imagem dos cálculos e eventuais arquivos ".m" utilizados na plataforma Moodle.

• Prova escrita A1
• Entrega do Projeto Final. O projeto é avaliado nos quesitos:

PFe - Documento de Especificação (apresentado no relatório);

PFp - Implementação do Projeto;

PFr - Relatório do Projeto (excluído a especificação);

PFi - Avaliação individual do aluno no projeto (conceito subjetivo atribuído pelo professor a partir da observação e da apresentação do projeto).

4 Referências Bibliográficas

Curso de Engenharia de Telecomunicações