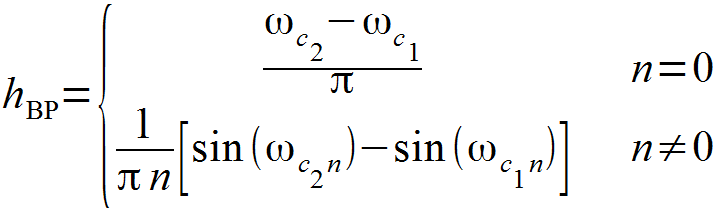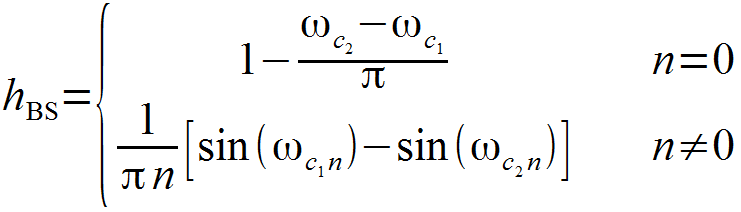Predefinição:DiegoMedeiros-PSD20706
Informações da disciplina
- Professor: Diego da Silva de Medeiros
- Plano de Ensino 2017-2
| Atividades previstas - Clicar no "+" para expandir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Planos de ensino anteriores - Clicar no "+" para expandir | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diário de aula
| 2017-2 - Clicar no "+" para expandir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2016-2 - Clicar no "+" para expandir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2016-1 - Clicar no "+" para expandir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2014-2 - Clicar no "+" para expandir | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2014-1 - Clicar no "+" para expandir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2013-2 - Clicar no "+" para expandir | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aulas
Apresentação da disciplina
- Roteiro:
- Apresentação do professor;
- Apresentação da Área de Processamento de Sinais (Slides)
- Apresentação da disciplina (Planos de ensino);
- Grupo da disciplina: IFSCTelePSD
- Atividade (Trabalho 1)
- Pesquisar um artigo da área de Processamento de Sinais no site IEEEXplore e fazer um pequeno resumo sobre o artigo. Como dica, dar preferências a artigos entre 1960 e 1970, pois estes deverão ser de mais fácil compreensão que artigos mais recentes ou muito antigos.
Tutorial de Matlab
Tutorial Linux.m Tutorial Windows.m Versão em PDF do tutorial
Sinais em tempo discreto
Referência: Capítulo 3 do Livro do Lathi, pg. 224.
Introdução à Sinais em Tempo Discreto
- Esta aula é a introdução da disciplina.
- Um sinal discreto é uma abstração de um sinal amostrado, que por sua vez é obtido a partir da multiplicação de um sinal contínuo por um trem de impulsos. A amostragem de sinais é assunto de outra disciplina (Sinais e Sistemas e Comunicação Digital).
- Uma das medidas do tamanho de um sinal é a energia e a potência.
- Energia do sinal:
- Potência do sinal:
- Desta forma, sinais podem ser divididos em sinais de energia ou de potência
- Sinais de energia são sinais que tem energia finita, que desta forma tem potência zero.
- Sinais de potência são sinais que tem potência finita, que desta forma tem energia infinita.
- Alguns sinais não são nem de energia nem de potência
- É comum na área de processamento de sinais a realização de operações com sinais. Algumas dessas operações utilizadas em sinais discretos são:
- Deslocamento - Atraso ou avanço de um sinal no tempo.
- Reversão no tempo - Espelhamento no sinal a partir do eixo da ordenada (y)
- Alteração na taxa de amostragem
- Decimação - Redução da frequência de amostragem do sinal
- Interpolação - Aumento da frequência de amostragem do sinal
- Códigos Matlab desenvolvidos
* Simulação.m * u.m * s.m
- Exercícios (Lathi)
* Exemplo 3.1, pg. 226 * Exemplo 3.2, pg. 227 * Exercício E3.1, ppg. 226 * Exercícios E3.2, E3.3, E3.4 e E3.5, pg. 230
Funções Úteis
- Alguns sinais úteis na área de processamento de sinais digitais (Seção 3.3, pg. 230, do Lathi).
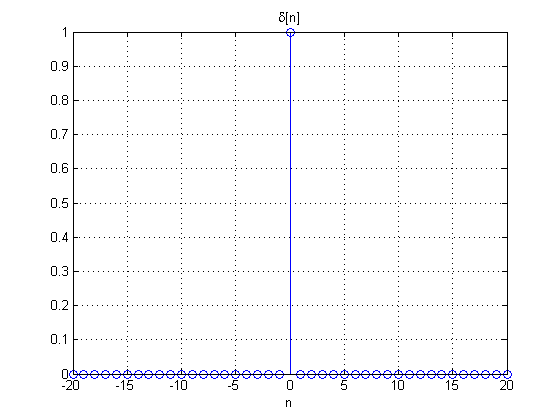
- Impulso unitário, também conhecido como Delta de Kronecker, é a versão discreta da Função Impulso, também conhecida como Delta de Dirac:
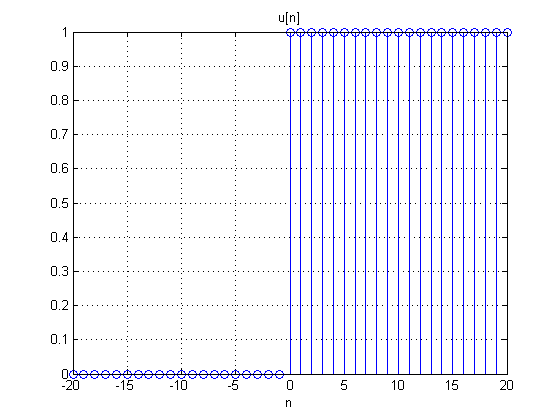
- Degrau unitário, versão discreta da Função Degrau. Muito utilizada para a limitação de sinais em um intervalo de tempo.
- Uma Função Exponencial discreta é descrita na forma , onde é o argumento da função e é inteiro. É possível escrever a função exponencial de uma outra forma, tendo em vista que a base e o argumento são constantes:
- A análise de funções exponenciais discretas é realizada baseada no valor de ou de . Iniciemos nossa análise considerando que , e por consequência , é real.
- Se , , de forma que é uma função crescente;
- Se , encontra-se entre 0 e 1, de forma que é uma função decrescente;
- Se , , de forma que é uma função constante igual a 1.
- A análise de funções exponenciais discretas é realizada baseada no valor de ou de . Iniciemos nossa análise considerando que , e por consequência , é real.
- Se é complexo, ele pode ser escrito na forma , e . Desta forma, também será complexo, ou . A análise é feita então em função de e .
- Se , a exponencial é puramente real, possuindo os três casos acima descritos;
- Se , e , sendo então uma função oscilatória complexa de módulo igual a 1 e frequência de oscilação igual a ;
- Se , e , sendo então uma função oscilatória complexa com módulo crescente e frequência de oscilação igual a
- Se , e , sendo então uma função oscilatória complexa com módulo decrescente e frequência de oscilação igual a
- Se é complexo, ele pode ser escrito na forma , e . Desta forma, também será complexo, ou . A análise é feita então em função de e .
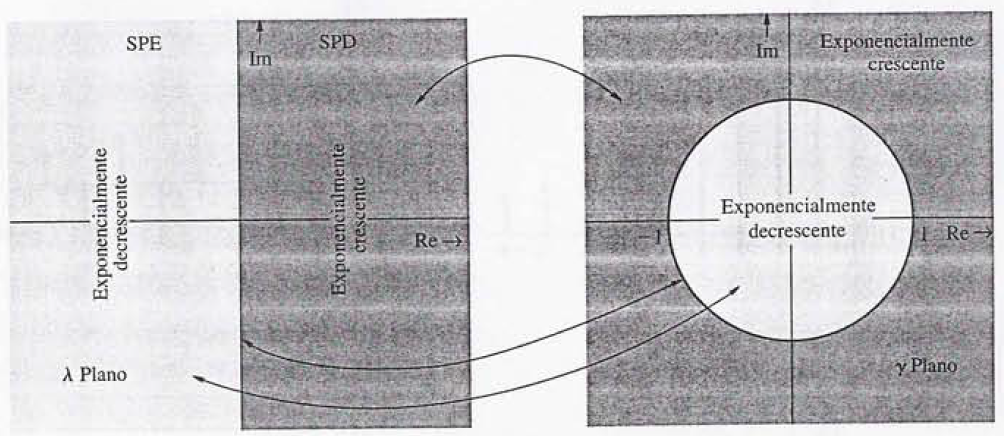
- A análise acima pode ser exportada para um gráfico, como pode ser visto na figura ao lado. Neste caso, o mapeamento de em transforma o Semi Plano Esquerdo (SPE), região onde a exponencial é decrescente, num círculo de raio unitário. O eixo das ordenadas, onde a exponencial possui módulo constante se transforma na borda do círculo. Por fim, o Semi Plano Direito (SPD), onde a exponencial é crescente, se transforma na região fora do círculo unitário.
- Códigos Matlab desenvolvidos
* Simulação.m * u.m * d.m * Comandos usados na aula
- Exercícios (Lathi)
* Exemplo 3.3, pg. 232 * Exercícios E3.6 e E3.7, pg. 234 * Exemplos de computador: * C3.1 para o sinal , mostrando o sinal no intervalo de 0 a 10 * C3.2 para o sinal , mostrando o sinal no intervalo de 0 a 33
Laboratório - Sinais digitais
- Laboratório 1 - Som
- Ler o arquivo de áudio abaixo
- Realizar operações de deslocamento, reversão no tempo, reversão de amplitude, mexer na frequência de amostragem, etc
* Codigo.m * Audio.mp3
- Laboratório 2 - Imagem
- Fazer partes 1 a 3 do laboratório acessível em Link
- Laboratório 3 - Interpolação de uma imagem
- Ler o arquivo de imagem abaixo
- Aumentar a resolução da imagem, através da interpolação
* Imagem.jpg * Codigo.m - Aula do dia 23/08/2016
Avaliação - Interpolação
Terminar o processo de interpolação iniciado em aula. Já foi feito o processo para linhas, fazer para colunas e diagonais.
* Codigo.m - Completo
Sistemas em tempo discreto
- Ao pensar em Sistemas de Tempo Discreto, normalmente vem à mente aplicações como áudio digital, imagem digital, etc. O termo discreto porém, é maior do que isso, e inclui todo sistema que é não contínuo. O exemplo abaixo, exemplo 3.4 do Lathi, aborda esta questão.
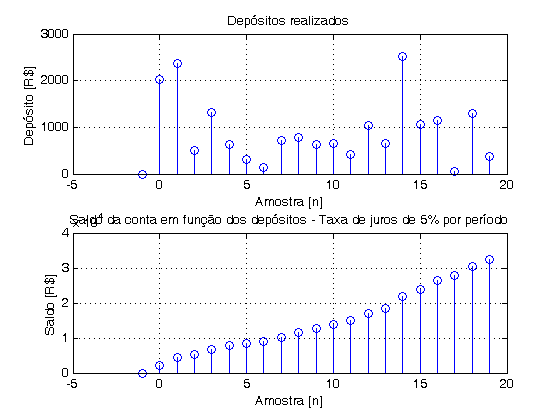
- Uma pessoa faz regularmente um depósito em um banco a um intervalo . O banco paga um certo juro na conta bancária durante o período e envia periodicamente uma correspondência com o saldo ao depositante. As variáveis envolvidas no problema são:
- = depósito feito no instante
- = saldo na conta no instante , calculado imediatamente após o recebimento do depósito
- = taxa de juros
- O saldo é a soma de:
- Saldo anterior
- Juros obtidos em durante o período
- Depósito
- A equação que relaciona a saída (saldo) com a entrada (depósito) é:
- , onde
- Ou, substituindo por
- , onde
- Uma pessoa faz regularmente um depósito em um banco a um intervalo . O banco paga um certo juro na conta bancária durante o período e envia periodicamente uma correspondência com o saldo ao depositante. As variáveis envolvidas no problema são:
- As equações anteriores, chamadas de equações diferença, relacionam a entrada e a saída de um sistema, ou de uma forma mais completa, relacionam as amostras atual e anteriores da entrada com as amostras atual e anteriores da saída. Uma versão genérica da equação diferença é:
- , com
- ou
- As equações anteriores estão na forma do operador de avanço. Substituindo por , a equação fica na forma do operador de atraso:
- , com
- Para que um sistema descrito pelas equações diferença acima descritas seja causal, é necessário que sua saída não dependa de valores futuros de sua entrada. Na forma do operador de avanço, a saída mais avançada no tempo é , e a entrada mais avançada no tempo é . Assim, para que um sistema seja causal, é necessário que
- Uma forma simples e rápida de resolver o sistema a partir da sua equação diferença é a solução recursiva (ou interativa). O método é calculado passo a passo, utilizando as condições iniciais e os valores do sinal de entrada.
Ver exemplo 3.8 do Lathi, pg. 247
- Uma forma diferente de representar o sistema é através da Notação Operacional. Nela, a equação diferença do sistema fica similar à uma equação diferencial, e um tratamento semelhante pode ser utilizado para sua resolução. Para a notação operacional, utiliza-se o operador para representar um avanço de amostras.
- Exemplo:
- Equação diferença de primeira ordem:
- Equação diferença de segunda ordem:
- Desta forma, uma equação diferença genérica em notação operacional é
- ou simplesmente
- onde
- Códigos Matlab desenvolvidos
* Simulação.m - Solução do exemplo 3.8
- Exercícios (Lathi)
* Exercício 3.4-1 e 3.4-2 pg. 295 * Exemplo 3.8, pg. 247 * Exercício E3.10, pg. 249 * Exemplo de computador C3.3 para o sinal do exercício E3.10 * Descrever todas as equações diferença dos exercícios anteriores com Notação Operacional
Solução de Sistemas e Resposta de Entrada Nula
- Saída de um sistema possui componentes referentes à entrada do sistema e componentes referentes às condições iniciais
- Referentes às condições iniciais: Resposta de entrada nula
- Referentes à entrada: Resposta de estado nulo
- A resposta de entrada nula de um sistema é a solução da sua equação diferença, assumindo que não há sinais de entrada (solução homogênea).
- ou
- ou ainda
- A solução do problema é então (assumindo raízes distintas):
- onde os 's são as constantes do problema, obtidas através das condições iniciais
- Para raízes repetidas:
- e a resposta de entrada nula será:
- Para raízes complexas, expressamos as raízes na forma polar:
- e
- E a resposta de entrada nula será
- Para um sistema real
- e
- E então:
- Nomenclatura:
- = polinônio característico do sistema
- = equação característica do sistema
- = raízes características, valores característicos ou autovalores do sistema
- = modos característicos ou modos naturais do sistema
- = resposta de entrada nula do sistema, que é a combinação linear dos modos característicos
- Exercícios (Lathi)
* Exemplo 3.10, pg. 252 * Exercícios E3.11, E3.12 e E3.13, pg. 255 * Exercício de computador C3.4 para os sistemas dos outros exercícios
Resposta ao Impulso e Resposta de Estado Nulo
- Uma solução importante na análise de sistemas é a resposta do sistema à um impulso unitário. A resposta ao impulso de um sistema é a solução da sua equação diferença, considerando que há, na entrada do sistema, uma função impulso .
- Ou:
- Neste caso, considera-se todas as condições iniciais nulas:
- O método iterativo (ou recursivo) pode ser utilizado para a resolução do sistema, mas este é pouco prático para respostas longas. Por isso, há a solução fechada, dada pela equação:
- onde é a combinação linear dos modos característicos e e são obtidos da equação diferença do sistema.
Ver exemplo 3.12, pg. 258
- A resposta de estado nulo é a resposta do sistema à sua entrada, considerando suas condições iniciais zero. A solução da resposta de estado nulo é dada pelo somatório de convolução:
- onde é a entrada do sistema e é sua resposta ao impulso. Embora pareça um pouco diferente, o somatório de convolução é a mesma operação realizada em tempo contínuo, a integral de convolução.
- As propriedades do somatório de convolução são:
- Comutativa
- Distributiva
- Associativa
- Propriedade do deslocamento
- Se ,
- Convolução com um impulso
- Propriedade da largura
- Se tem elementos (amostras) e tem elementos, tem elementos.
- Causalidade
- para
- para , tal que para
- E a convolução causal é:
Ver exemplo 3.13, pg. 262
- Em geral, o cálculo da convolução propriamente dito não é muito realizado. Isso se deve à existência de tabelas com a convolução dos sinais mais comuns. Um exemplo pode ser visto na Tabela 3.1 do livro do Lathi, pg. 263.
- Mais importante que a resolução dos cálculos, seja pela equação ou pela tabela, é o entendimento do que é realizado com os sinais durante a operação. A convolução de dois sinais e inicia com a reversão no tempo de um dos sinais (por exemplo, ). Para encontrar o valor de saída para um dado instante , é deslocado de amostras, e uma multiplicação ponto a ponto é executada entre os sinais e . O processo de convolução consiste então no deslocamento de por toda a extensão de . Este fato pode ser visto em [1] e [2].
- Exercícios (Lathi)
* Exemplo 3.11, pg. 256 * Exemplo 3.12, pg. 258 * Exercício E3.14, pg. 259 * Exercício 3.7-4, pg. 298 * Exemplo 3.13, pg. 262 * Exercício E3.15, pg. 263 * Exemplo 3.14, pg. 264 * Exemplo de computador C3.6 * Criar uma função no Matlab para realizar a convolução entre dois sinais causais
Laboratório - Reposta ao impulso
- Parte 1 - Em sala
- Criar respostas ao impulso com poucos multipercursos:
d = zeros(30000,1); d(1) = 1; d(15000) = 1;
- Ler um arquivo de áudio e realizar a convolução entre ele e a resposta ao impulso criada
- Observar o comportamento
- Parte 2 - Entregar
Construir uma simulação no Matlab que lê um dos arquivos de áudio e cria um efeito de que a voz foi falada à 45° do ouvinte (estéreo).
| Comentários - Clicar no "+" para expandir |
|---|
|
Observa-se que o efeito de 45° de ângulo de incidência é difícil de ser implementado com os conceitos abordados em aula. A alteração para 90° permite um certo nível de sucesso. Para a implementação do ângulo de 45° seria necessário usar o método das imagens de Allen e Berkley (ver artigo). |
Resposta Total e Estabilidade
- A Resposta total de um sistema é definida como:
- Resposta Total = Resposta de entrada nula + Resposta de estado nulo
- Resposta Total =
- A estabilidade de um sistema é dividida entre estabilidade externa (BIBO - Bounded-input/boundded-output) e interna (assintótica).
- Um sistema é BIBO estável se a sua resposta ao impulso for absolutamente somável:
- A estabilidade interna de um sistema é caracterizada da seguinte forma:
- Raízes simples ou repetidas dentro do círculo unitário: assintoticamente estável
- Raízes simples sobre o círculo unitário: marginalmente estável
- Raízes repetidas sobre o círculo unitário: assintoticamente instável
- Raízes simples ou repetidas fora do círculo unitário: assintoticamente instável
- As estabilidades interna e externa são relacionadas da seguinte forma:
- Raízes dentro do círculo são absolutamente somáveis, por isso sistemas assintoticamente estáveis são BIBO estáveis.
- Raízes sobre ou fora do círculo não são absolutamente somáveis, por isso sistemas marginalmente estáveis ou assintoticamente instáveis são BIBO instáveis.
- Exercícios (Lathi)
* Exemplo 3.22, pg. 285 * Exercício 3.10-2, pg. 303
Avaliação 1 - Sinais e sistemas de tempo discreto
- Os conteúdos referentes à primeira parte da disciplina (capítulo 3 do Lathi) serão avaliados através de uma prova.
Para 2016-2, a prova será aplicada no formato de um trabalho, com prazo para entrega em 30/09/2016.
| Resultados - Clicar no "+" para expandir |
|---|
|
|
Transformada Z
Referência: Capítulo 5 do Livro do Lathi, pg. 442.
Definição da Transformada Z Direta e Inversa
- A Transformada Z Direta é calculada como a seguir:
- A forma mais direta de resolução se dá considerando que os termos a serem somados são elementos de uma PG (progressão geométrica). Uma PG é definida como uma sucessão de termos:
- onde, ou , sendo denominado razão da sucessão de termos.
- A planilha a seguir foi feita para ajudar o entendimento das PGs, confirmando a equivalências das duas equações acima Link.
- Para a soma de termos de uma PG ( finito):
- Para a soma de infinitos termos de uma PG:
- Para mais informações sobre PGs, ver Link.
- A Transformada Z inversa é definida como:
- Em geral este cálculo não é realizado, dada a existência de tabelas (ver tabela 5.1 do Lathi ou esta seção da Wikipédia). O que é necessário para a resolução dos problemas é adequar o sinal no domínio Z à algum par específico da tabela.
- Exercícios (Lathi)
* Exemplo 5.1, pg. 444 * Exemplo 5.2, pg. 446 * Exercício E5.1, pg. 448 * Selecionar alguns itens do exercício 5.1-2, pg. 516 * Exercício 5.1-4, pg. 517
* Exemplo 5.3, pg. 448 * Exercício E5.2, pg. 451 * Exercício 5.1-5, pg. 517
- Resoluções realizadas no semestre 2013-1
- Solução exemplo 5.3.b
- Solução exemplo 5.3.c
Propriedades da Transformada Z
- Algumas propriedades podem ser utilizadas para facilitar o cálculo da transformada Z. Exemplos de tabelas são a Tabela 5.2, pg. 459 do Lathi e esta seção da Wikipédia.
- Nesta aula, as propriedades serão derivadas.
- Exercícios (Lathi)
* Exemplo 5.4, pg. 456 * Exercício 5.2-3, 5.2-7 e 5.2-9, pg. 518
Solução de sistemas usando a Transformada Z
- A Transformada é utilizada principalmente na solução de sistemas Lineares Discretos Invariantes no Tempo (LDIT). O método é sintetizado a seguir:
- A equação diferenças é convertida para o domínio utilizando a propriedade do deslocamento à direita da Transformada Z:
- A equação algébrica no domínio é trabalhada de forma a isolar .
- Com o isolado, a equação algébrica é convertida de volta para o domínio através da Transformada Z Inversa, encontrando então a resposta total do sistema, .
- Com esta abordagem, é possível também encontrar a resposta total com as componentes de entrada nula e de estado nulo em separado. Para isso, as componentes referentes ao sinal de entrada e às condições iniciais devem ser mantidas separadas durante o trabalho algébrico.
- Uma outra utilização da Transformada Z diz respeito à Função de transferência de um sistema. A Função de Transferência é utilizada para encontrar a a resposta de estado nulo do sistema, ou mesmo a resposta total, quando o sistema não possui condições iniciais (resposta de entrada nula igual à zero):
- então:
- Dada a equação diferenças genérica:
- ou, em notação operacional:
- ou simplesmente:
- onde:
- A Função de Transferência do sistema é:
- A estabilidade do sistema pode ser obtida a partir da sua Função de Transferência. Como a Função de Transferência é uma descrição externa do sistema, pois relaciona saída e entrada, a estabilidade BIBO (externa) é encontrada. Assim, se todos os polos de estiverem dentro do círculo unitário, o sistema será BIBO estável.
- Se e não possuírem fatores comuns, o denominador de será idêntico à , e:
- sistema assintoticamente estável: Polos de , repetidos ou simples, dentro do círculo unitário
- sistema assintoticamente instável:
- (i) Ao menos um polo de fora do círculo unitário;
- (ii) Polos de repetidos sobre o círculo unitário
- sistema marginalmente estável: Nenhum polo de fora do círculo unitário e pelo menos um polo simples sobre o círculo unitário.
- Exercícios (Lathi)
* Exemplo 5.5, pg. 461 * Exercício E5.10, pg. 462 * Exercício E5.11, pg. 463 * Exercício E5.12, pg. 464 * Exercícios 5.3-2, 5.3-3, 5.3-5, 5.3-6, 5.3-7, 5.3-8, 5.3-10, pg. 519
* Exemplo 5.6, pg. 466 * Exercício 5.3-18, pg. 519 * Exercícios 5.3-19, 5.3-20, 5.3-21, 5.3-23, pg. 520
- Resoluções realizadas no semestre 2014-1
- Solução exercício E5.10
Resposta em Frequência de Sistemas em Tempo Discreto
- A Resposta em Frequência de um sistema de Tempo Discreto é encontrada a partir da sua Função de Transferência, substituindo por . Assim, a frequência é indicada por . Usando a seta direcional para representar a relação entrada saída:
- E, fazendo :
- onde é a Resposta em Frequência do sistema, que expressa na forma polar:
- Para uma entrada senoidal, considerando que é a parte real de :
- e para uma senoide defasada de :
Ver Exemplo 5.10 do Lathi, pg. 476
- Como pode ser visto no exemplo anterior, a Resposta em Frequência de Sistemas de Tempo Discreto é Periódica com período . Isto se deve à não unicidade de ondas senoidais no domínio de tempo contínuo:
- , para inteiro
- Isto pode ser confirmado pelo seguinte Código MATLAB.
- A Resposta em Frequência do sistema também pode ser determinada pela posição dos seus polos e zeros. Para uma Função de Transferência genérica:
- encontrando as raízes de ambos os polinômios, a Forma Fatorada da Função de Transferência é encontrada:
- Para encontrar a Resposta em Frequência do sistema, fazemos . Como , variar significa percorrer o círculo unitário. Desta forma, a resposta do sistema para uma determinada frequência é encontrada a partir da linha que une os polos e zeros ao ponto de ângulo sobre o círculo unitário. Ou:
- ou
- onde e são os módulos e e são os ângulos da linha que une o zero e o polo ao ponto de ângulo sobre o círculo unitário.
- Desta forma, as seguintes conclusões podem ser tomadas
- Como a magnitude de é diretamente proporcional ao produto das distâncias dos zeros à , incluir um zero próximo de um determinado ângulo do círculo unitário reduz a resposta de magnitude para esta frequência angular. Para suprimir totalmente uma determinada frequência, um zero neste ângulo do círculo unitário pode ser inserido.
- Como a magnitude de é inversamente proporcional ao produto das distâncias dos zeros à , incluir um polo próximo de um determinado ângulo do círculo unitário aumenta a resposta de magnitude para esta frequência angular. Não se deve esquecer que um polo sobre o círculo unitário resulta num sistema BIBO instável.
- Para um filtro ideal, o número de polos e zeros necessários é muito grande (infinito).
- Este comportamento pode ser visto na ferramenta do MATLAB Fdatool.
- Exercícios (Lathi)
* Exemplo 5.10, pg. 476 * Exercício E5.18, pg. 479 * Exercícios 5.5-1, 5.5-2, 5.5-4, pg. 521 * Exercícios 5.5-5, pg. 522
* Exercício 5.6-1, pg. 522
Laboratório de Transformada Z
- Este laboratório tem o objetivo de auxiliar o entendimento dos conceitos que envolvem a utilização da Transformada Z na análise e solução de sistemas LDIT. Mais precisamente, a Função de Transferência será explorada, de forma a visualizar a resposta em frequência a partir da posição dos polos e zeros do sistema.
- Pré laboratório
- Estudar o help do matlab das funções:
- polar() - Plot em coordenadas polares
- poly() - Encontra os coeficientes de um polinômio com base em suas raízes
- roots() - Encontra as raízes de um polinômio com base em seus coeficientes
- freqz() - Retorna a resposta em frequência de um sistema com base na sua equação diferença
- Laboratório
- Definir os seguintes sistemas com o mínimo de polos e zeros:
- Filtro passa-baixas
- Filtro passa-altas
- Filtro passa-faixa
- Filtro rejeita-faixa
- Plotar os polos (x) e os zeros (o) no círculo unitário usando a função polar()
- Calcular a resposta em frequência do filtro criado utilizando a função freqz()
- Observar a definição da frequência de amostragem nos parâmetros.
- Plotar a resposta de magnitude e de fase dos filtros
- Aumentar o número de polos e zeros dos filtros e observar o comportamento
Avaliação 2 - Transformada Z
- Os conteúdos referentes à segunda parte da disciplina (capítulo 5 do Lathi) serão avaliados através de uma prova.
| Resultados - Clicar no "+" para expandir |
|---|
|
|
Análise de Fourier de Sinais em Tempo Discreto
Referência: Capítulo 9 do Livro do Lathi, pg. 738.
Série de Fourier de Tempo Discreto
- Periodicidade de uma senoide discreta
- Uma senoide discreta é periódica com período inteiro se . Esta equação é verdadeira quando , com inteiro. Assim, a senoide será periódica se:
- um número racional (representado pela divisão de dois números inteiros)
- O Período Fundamental da senoide será então:
- sendo a Frequência Fundamental da senoide e o menor inteiro que faz um número inteiro.
- O Período Fundamental da senoide será então:
- Definição da Série de Fourier de Tempo Discreto
- A Série de Fourier de Tempo Discreto é constituída pela soma de exponenciais complexas e discretas, com frequências múltiplas da frequência fundamental:
- Mas como:
- A Série de Fourier de Tempo Discreto é finita, com termos.
- Mas como:
- A Série de Fourier de Tempo Discreto é definida por:
- onde é o coeficiente associado à frequência angular , definido por:
- Espectro de Fourier de um Sinal Discreto
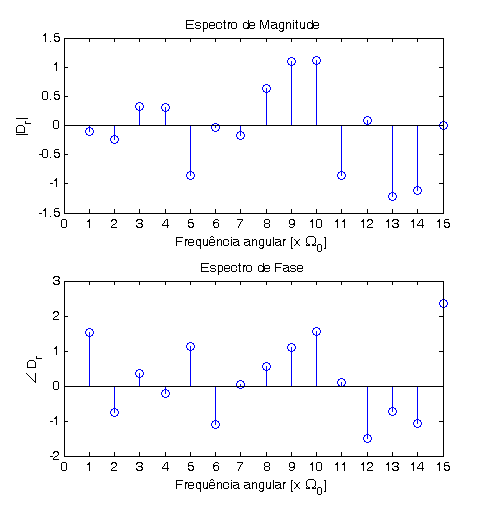
- A Série de Fourier tem componentes:
- onde as frequências de cada componente. Considerando que é em geral complexo, na forma
- Pode-se então fazer um gráfico relacionando o módulo e a fase de com a frequência do termo. Este é o Espectro de Fourier do sinal.
- Códigos Matlab desenvolvidos
* Periodicidade_senoide.m * Espectro_Fourier.m -- Simples * ExemploC9_2.m * Espectro_Fourier_3D.m * Espectro_Fourier_3D_onda_quadrada.m
- Exercícios (Lathi)
* Exemplo 9.2, pg. 745 * Exercício E9.2, pg. 744 * Exercício 9.1-1, 9.1-4, 9.1-5 e 9.1-6, pg. 783
Transformada de Fourier de Tempo Discreto
- As Séries de Fourier de Tempo Discreto permitem descrever sinais discretos periódicos através da soma de exponenciais complexas. Quando o sinal é aperiódico a utilização da série é inviabilizada. A extensão da análise de Fourier para sinais discretos aperiódicos é feita da mesma forma que no mundo contínuo, formando um sinal aperiódico a partir de um sinal periódico com período infinito.
- Sendo assim, o par de Transformadas de Fourier é definido como:
- Transformada Direta
- Transformada Inversa
- Informações relevantes
-
- Espectro é uma função contínua de
- Espectro é uma função periódica de :
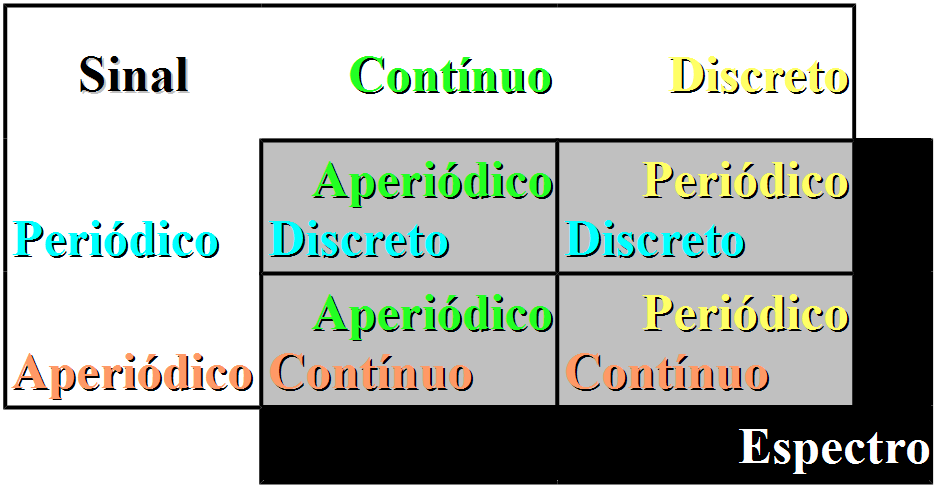
- Espectro Periódico X Amostrado
- Sinal periódico:
- Séries de Fourier
- Espectro discreto (harmônicas)
- Sinal aperiódico:
- Espectro contínuo
- Sinal discreto (amostrado)
- Espectro periódico (repetido a cada Hz ou )
- Sinal contínuo
- Espectro aperiódico
- Exercícios (Lathi)
* Exemplo 9.3, pg. 752 * Exemplo 9.4, pg. 753 * Exemplo 9.5, pg. 754 * Exemplo 9.6, pg. 756 * Exercício E9.4 e E9.5, pg. 756
Laboratório de Transformada de Fourier
- Criação de sinais digitais no Matlab.
- Funções do Matlab apresentadas:
linspace() - função utilizada para criar vetores em intervalos lineares fft() - função que calcula a transformada de Fourier fftshift() - função auxiliar no trabalho com a transformada de Fourier
| Código executado em sala |
|---|
clear all; close all
% Amostragem
fs = 5000;
ts = 1/fs;
% Numero de amostras do seno
N = 10000;
% Criando o vetor de tempo
n = 0:N-1;
t = linspace(0,(N-1)*ts,100000);
% Criando o vetor de frequencia
f = linspace(-fs/2,fs/2,N);
% Parametros dos senos - cada elemento do vetor
% irá criar um seno diferente, e todos serao somados
A = [1 0.5 0.25 0.5];
fo = [50 200 450 900]; % Hz
% Iniciando o sinal
sinal = zeros(size(n));
sinal_plot = zeros(size(t));
for ii = 1:length(A)
% Gerando o sinal senoidal
sinal = sinal + A(ii) * sin(2*pi*fo(ii)*n*ts);
sinal_plot = sinal_plot + A(ii) * sin(2*pi*fo(ii)*t);
end
% Exibindo o sinal no tempo
figure
stem(n*ts,sinal,'Marker','none')
hold on
plot(t,sinal_plot,'k')
xlabel('Tempo [s]')
ylabel('Sinal')
% Tirando a transformada de fourier
espectro = (2/N)*fft(sinal);
% Exibindo o sinal na frequencia
figure
plot(f,fftshift(abs(espectro)))
% Tocando o sinal na caixa de som
sound(sinal,fs)
%% Receber tecla do usuário
%
% Tecla digitada está armazenada na variável "x", como um texto
x = input('Digite uma tecla > ','s');
display(['A tecla digitada foi: ' x])
%% Juntando os dois códigos
%
% Usar CTRL+c para interomper
while true
x = input('Digite uma tecla > ','s');
display(['A tecla digitada foi: ' x])
end
%% Controlando a execução do laço
%
% Usar a tecla "q" para sair do laço
% Iniciando o "x"
x = ' ';
while x ~= 's'
x = input('Digite uma tecla > ','s');
display(['A tecla digitada foi: ' x])
end
%% Estrutura de teste
%
mynumber = input('Enter a number: ');
switch mynumber
case 1
disp(' Digitou 1');
case 2
disp(' Digitou 2');
case 3
disp(' Digitou 3');
case 4
disp(' Digitou 4');
case 5
disp(' Digitou 5');
case 6
disp(' Digitou 6');
case 7
disp(' Digitou 7');
case 8
disp(' Digitou 8');
case 9
disp(' Digitou 9');
otherwise
disp(' Other value');
end
|
Avaliação 3 - Trabalho sobre Transformada de Fourier
| Atividades dos semestres anteriores - Clicar no "+" para expandir |
|---|
Laboratório de Processamento Digital de Imagens
Este laboratório é uma apresentação da Área de Processamento Digital de Imagens. É baseado em alguns materiais de alunos do professor Manuel Menezes de Oliveira Neto (página), da UFRGS. (Colorização)
Filtros Digitais
Referência: Capítulo 4, 5 e 6 do Livro do Shenoi.
Introdução aos Filtros Digitais
- As respostas clássicas de filtros analógicos também se aplicam aos filtros digitais:
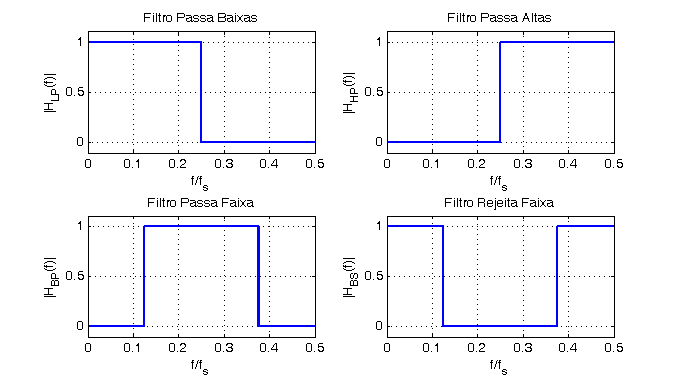
- Os filtros digitais são sistemas descritos por equações diferenças, que na sua forma genérica é:
- A Função de Transferência dos filtros digitais é encontrada via Transformada Z:
- Fazendo , obtemos a Resposta em Frequência do filtro:
- Nota-se que é um número complexo, que pode então ser descrito na forma polar:
- onde é o módulo da resposta em frequência (Resposta de Magnitude) e é a fase da resposta em frequência (Resposta de Fase).
- O processo de filtragem de um sinal por um filtro digital é descrito através da operação de convolução. "Filtrar" um sinal significa realizar a convolução da resposta ao impulso do filtro com o sinal em questão:
- Que no domínio da frequência é:
- ou:
- Ou seja, o espectro de magnitude do sinal filtrado é o produto do espectro de magnitude do sinal original pela resposta de magnitude do filtro, enquanto que o espectro de fase do sinal filtrado é a soma do espectro de fase do sinal original pela resposta de fase do filtro.
Filtros FIR e IIR
- Os filtros FIR e IIR serão apresentados através dos dois seguintes exemplos:
- Exemplos
- , tendo como condições iniciais e , e sinal de entrada
- O resultado deste exemplo é
- , com sinal de entrada
- O resultado deste exemplo é
- É visível que há diferenças nos resultados dos exemplos. No primeiro exemplo, o sinal de saída inicia em e se estende até o infinito, dado que não há nenhuma limitação no tempo na equação. Já no segundo exemplo, o sinal de saída é limitado a existir apenas nos instantes e . Sendo assim, temos no primeiro exemplo um sinal de duração infinita e no segundo um sinal de duração finita. Como o sinal de entrada dos sistemas é um impulso (), os sinais em questão são as respostas ao impulso dos respectivos sistemas.
- Sendo assim, os filtros são classificados numa das duas formas:
- Filtros com Resposta ao Impulso Finita (FIR - Finite Impulse Response)
- Filtros com Resposta ao Impulso Infinita (IIR - Infinite Impulse Response)
Filtros FIR janelados
- A resposta de magnitude ideal de um filtro passa baixas pode ser descrita através da seguinte equação:
- Ao calcular a transformada inversa de Fourier da resposta em questão, o seguinte sinal é obtido:
- ou de outra forma:
- Para outros filtros:
- Filtro passa altas:
- Filtro passa faixa:
- Filtro rejeita faixa:
- Observação: Todas essas equações consideram o uso de uma frequência de amostragem . Caso uma outra frequência de amostragem seja utilizada, cuidar com as seguintes situações:
- A distância entre as amostras não serão de uma unidade. Assim, sempre que o termo aparecer, este deve ser substituído por . Com isso, a distância entre as amostras irá depender da frequência de amostragem utilizada.
- No filtro rejeita faixa, o termo em da subtração deve ser substituído pela frequência de amostragem, ficando a equação
- Estas são as respostas ao impulso dos filtros ideais. Uma questão importante destas respostas é que elas são ilimitadas no tempo, ou seja, possuem duração infinita. Para que estas repostas sejam realizáveis através de filtros FIR, é necessário limitar o número de amostras da resposta ao impulso :
- ou seja, amostras fora do intervalo são descartadas.
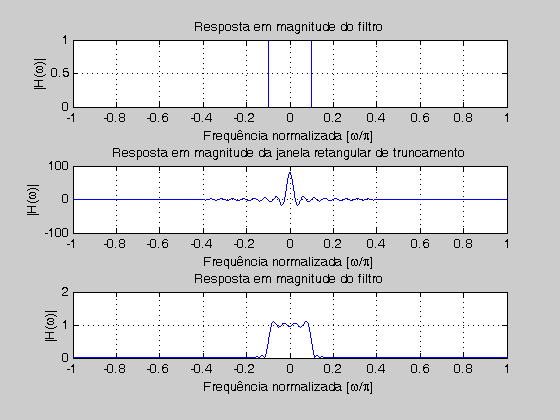
- Um filtro passa baixas truncado não possui mais a resposta em frequência ideal, já que para obter aquela resposta seriam necessárias infinitas amostras. Considerando que o truncamento pode ser representado pela multiplicação da resposta ao impulso original por uma janela retangular:
- a resposta em frequência do filtro truncado será a convolução da resposta em frequência ideal do fitro pela transformada de fourier da janela retangular utilizada no truncamento da resposta. Ou:
- onde é a transformada de Fourier da janela retangular:
- A janela retangular não é a única opção de truncamento disponível. A seguir, as principais janelas serão apresentadas:

- Bartlett (triangular):

- Hann:
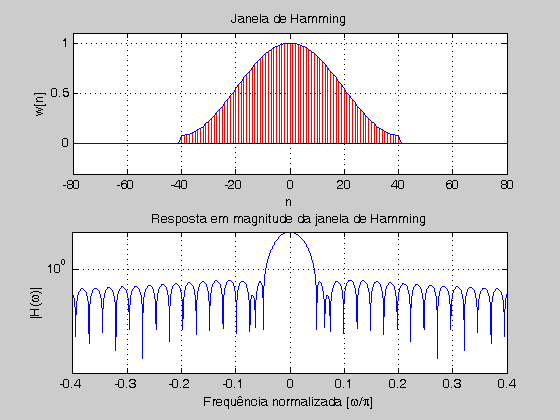
- Hamming:
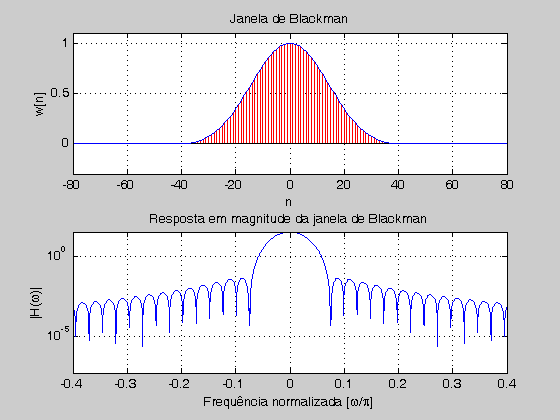
- Blackman:
- Os impactos do uso destas e muitas outras janelas podem ser vistos no Matlab, na ferramenta fdatool. Para mais informações, ver Link.
- Códigos Matlab desenvolvidos
* Simulação.m * u.m * d.m
A janela Kaiser
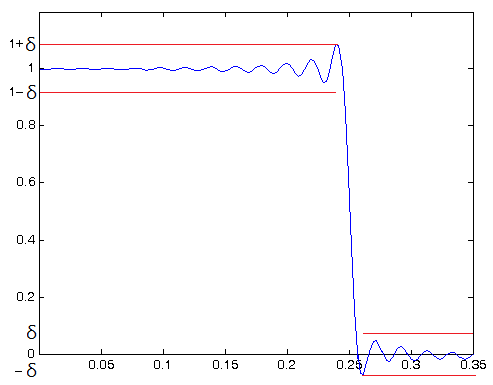
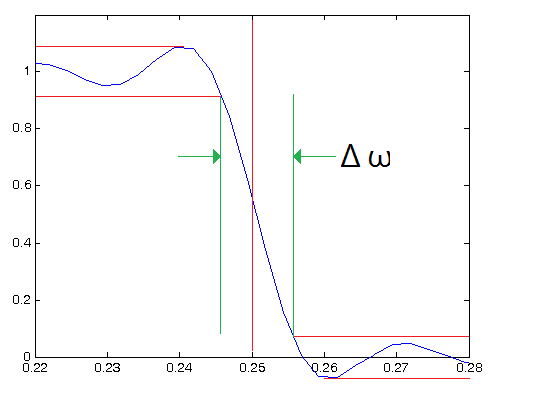
- Nas janelas anteriores não há um controle sobre a resposta em frequência dos filtros. Visando obter tal controle, a janela de Kaiser foi desenvolvida.
- Na janela de Kaiser, o parâmetro é utilizado para indicar a máxima flutuação da resposta nas bandas de rejeição e passagem, assim como o parâmetro indica a taxa de transição entre as duas bandas. Desta forma têm-se um controle total sobre a resposta em frequência do filtro.
- Para encontrar a resposta ao impulso da Janela de Kaiser, deve-se seguir os passos:
- Número de amostras da resposta ao impulso
- Janela de Kaiser:
- onde:
- Função de Bessel de ordem zero modificada (para fazer no Matlab, ver função besseli)
Laboratório de Filtros Digitais
Avaliação 4 - Filtros Digitais
| Semestres anteriores - Clicar no "+" para expandir |
|---|
|
Avaliações de Recuperação
| Avaliações semestres anteriores - Clicar no "+" para expandir |
|---|
|