CIL29003-2015-1
1 Dados Importantes
Professor: Odilson Tadeu Valle
Email: odilson@ifsc.edu.br
Atendimento paralelo: 2ª das 17h35 às 18h30 e 6ª das 9h40 às 10h35. Local: Lab. de Desenvolvimento.
- Avaliações
- 3 avaliações (P1, P2 e P3) mais um projeto final (PF).
- Cada uma das avaliações terá terá um conceito numérico: A, B, C e D. Conceito mínimo para não necessitar reavaliação: C.
- Um ou mais conceitos D implica na realização da reavaliação: uma única a ser realizada no último dia de aula.
IMPORTANTE: o direito de recuperar uma avaliação em que se faltou somente existe mediante justificativa reconhecida pela coordenação. Assim, deve-se protocolar a justificativa no prazo de 48 horas, contando da data e horário da avaliação e aguardar o parecer da coordenação.
1.1 Plano de Ensino
Cronograma_de_atividades_(CIL-EngTel)
1.2 Procedimento para acessar IFSC-Cloud
Siga exatamente TODOS os passos. Caso tenha algum problema com a senha, entre em contato com o professor
1.3 Listas de exercícios
| Lista para a primeira avaliação |
|---|
|
| Lista para a segunda avaliação |
|---|
|
| Lista para a terceira avaliação |
|---|
|
2 Diário de aulas
| Aula 1 - 3/2/15: Apresentação da disciplina |
|---|
|
| Aula 2 - 5/2/15: Sistemas de numeração Binário, Octal, Hexadecimal e conversão entre sistemas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2.1 Sistemas de numeraçãoObserve a Figura do odômetro. Supoha que o mesmo possua somente duas roldanas de algarismos e que cada algarismo represente exatamente 1 km. Qual a quantidade máxima de quilômetros que o suposto odômetro pode representar?
Agora suponha que cada roldana tenha impresso somente os valores 0 e 1. Qual a quantidade máxima de quilômetros que o mesmo pode representar?
Obs.: LSB (least significant bit) é o bit menos significativo que é o equivalente as unidades na representação decimal. MSB (most significant bit) é o bit mais significativo e sempre ocupa a posição mais a esquerda da representação. Este sistema de numeração é conhecido como binário ("que tem aspecto dual, ou é formado por dois elementos ou partes"). No caso anterior como poderíamos representar maiores quantidades de quilômetros? Em outra linha de raciocínio, como pode-se aumentar a capacidade de contagem quilométrica, mais do que o permitido no sistema decimal? Aumenta-se o número de símbolos disponíveis em cada roldana. Por exemplo, se adotarmos a seguinte simbologia: 0, 1, ..., 8, 9, A, B, C, D, E, F, pode-se ter a seguinte representação quilométrica:
Este é o sistema de numeração hexadecimal. Um outro importante sistema de numeração é o octal. Perceba que é possível a construção de qualquer sistema de numeração. 2.2 Conversão entre sistemas de numeraçãoComo é de conhecimento geral, o sistema de numeração mais utilizado port seres humanos é o sistema decimal. Não tão conhecido assim, mas muito utilizado, é o sistema de numeração binário, amplamente adotado nos sistema informatizados. Uma pergunta que cabe é, por exemplo, quando digitamos algum número em uma calculadora, o que acontece? Em primeiro lugar, a calculadora apresenta o valor digitado no visor, para termos certeza do que digitamos e, em seguida, internamente à calculadora este valor é convertido para binário, o sistema de numeração que ela entende. Como esta conversão ocorre? 2.2.1 Conversão de outras bases para a base decimalA regra geral para conversão de binário para um número decimal é assim expressa:
onde é um número decimal e é sua representação binária usual. Observe que esta regra pode ser estendida para qualquer sistema de numeração. Por exemplo, vamos converter para a base decimal.
Outro exemplo, vamos converter para a base decimal.
2.2.2 Conversão da base decimal para outras basesA conversão de um número da base decimal para qualquer outra base pode ser efetivada usando-se divisões sucessivas do valor decimal pela base a ser convertido, tomando-se com resultado os sucessivos restos dessa divisão. Por exemplo, para converter 23 para a base binária devemos fazer o seguinte procedimento: O procedimento para outras bases é o mesmo, por exemplo, para converter-se 258 para a base 8, utiliza-se o mesmo procedimento acima, substituindo os valores 2 por 8, no divisor. 2.2.3 Conversão entre bases de origem bináriaPara conversão entre as bases binária, octal e hexadecimal, basta fazer-se o uso das seguintes tabelas de conversão.
Por exemplo, para converter para binário, deve-se tomar dígito a dígito da tabela acima e ir montando o valor binário equivalente: , e . Portanto o resultado da conversão é Se desejarmos converter da base octal para a hexadecimal e vice-versa, a maneira mais fácil é primeiro a conversão da base de origem para a base binária e, em seguida, desta para a base destino. Por exemplo, para converter para a base octal procedemos primeiro a conversão para a base binária () e em seguida, tomando três a três dígitos a partir do LSB, convertemos para o octal usando a tabela, resultando em |
| Aula 3 - 5/2/15: Representações binárias | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
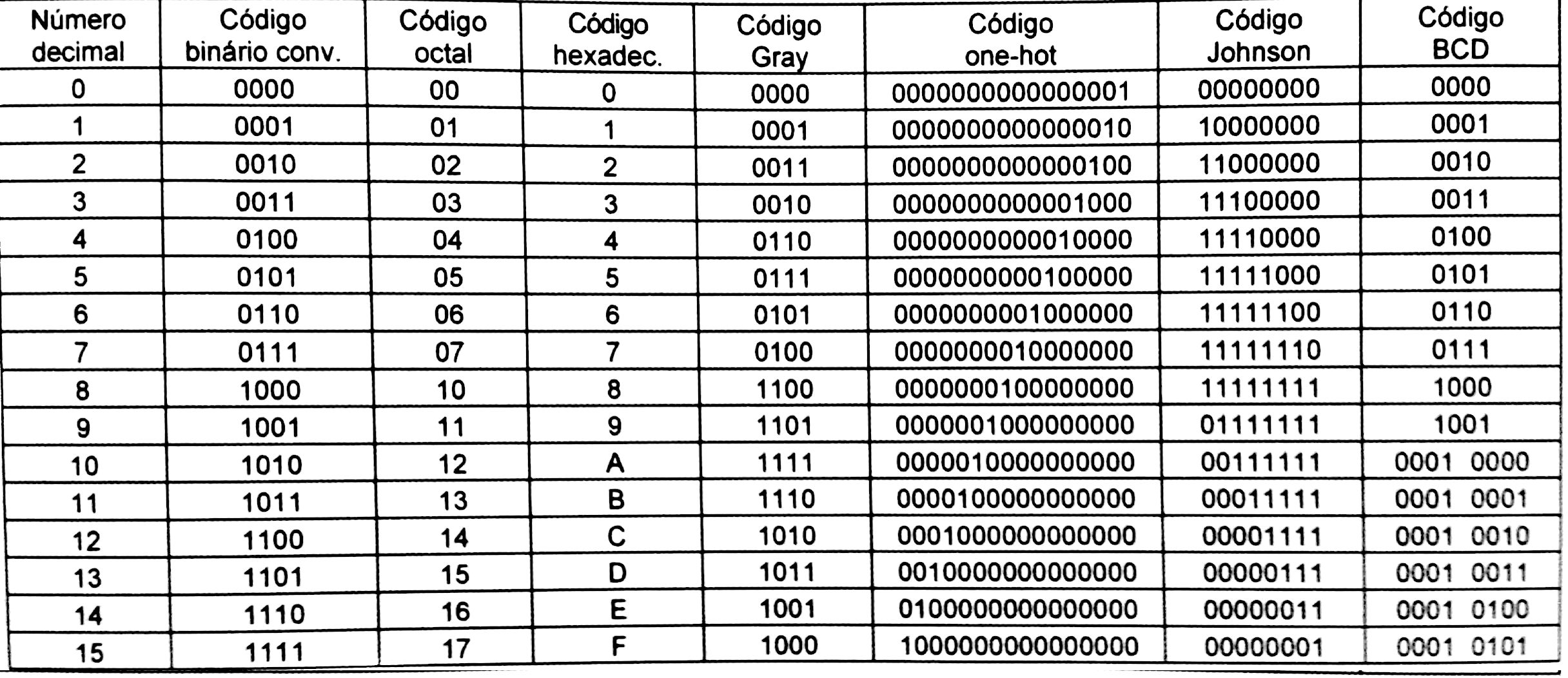
A tabela a seguir representa os númerios decimais de 0 a 15 pelos códigos binário convencinal, octal, hexadecimal, Gray, one-hot, Johnson e BCD.
Código Gray: código de distância unitária porque a distância entre duas palavras adjacentes é sempre 1 bit [1]. Código one-hot: frequentemente utilizado na codificação de máquinas de estados [2] [3]. Código Johnson: Também utilizado para representar máquinas de estados. É um código intermediário entre o one-hot e o Gray, em termos de uso do hardware. Código BCD (binary-coded decimal): cada dígito de um número decimal é representado por um conjunto de 4 bits do código binário. 2.3 Códigos para números negativosComo representar sinal no código binário? 2.3.1 Código sinal-magnitudeNesse caso o MSB representa o sinal: 0 = + e 1 = -. Assim sendo, o MSB não faz parte da representação sequencial binária do número. Ex:
2.3.2 Código complemento de umSe o MSB for 0 (número positivo), para obter o equivalente negativo, basta inverter todos os bits. Ex:
2.3.3 Código complemento de doisEsta é a opção adota para representar números negativos em praticamento todos os computadores e outros sistema digitais. A representação binária de um número negativo é obtida tomando sua representação positiva, invertendo todos os bits e então adicionando um a ele. Exemplo, -7 (5 bits) é igual a 00111 ==> 11000 + 1 ==> 11001 Regra prática Para cálculo do equivalente decimal de um número representado em complemento de dois, pode-se fazer uso do modelo apresentado no exemplo:
Ao somar-se todos os valores da segunda linha da tabela acima, obtém-se o valor 19. Usando números de 8 bits, Calcule o complemento de dois para:
Algum problema? |
| Aula 4 - 13/2/15: Ponto fixo e ponto flutuante | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Como é a representação (e conversão para decima) de um número binário fracionário? 2.4 Representação por ponto fixoA representação segue a regra
onde:
Por exemplo:
Portanto o decimal equivalente é: 29,625 2.5 Representação por ponto flutuanteComo representar número inteiros? Padrão IEEE 754
onde:
Observe que tem-se 32 bits totais para a precisão simples e 64 bits para a precisão dupla. 2.5.1 Precisão simplesO número decimal equivalente é obtido por:
Ex1: Encontre o valor decimal equivalente para o valor abaixo que está em ponto flutuante com precisão simples. 10111111110...0 Analisando o número acima obtemos: S = 1, E = 01111111 = 127, F = 10...0 = = 0,5. Portanto
Ex2: Encontre o valor decimal equivalente para o valor abaixo que está em ponto flutuante com precisão simples. 010000001010...0 2.5.2 Precisão duplaO número decimal equivalente é obtido por:
Observações:
Ex: determinar as representações binárias por ponto flutuante de precisão simples para: -2,625 = -2 + 1/2 + 1/8 = -21/8 = portanto S=1, F=0101..., E=128 (10000000), já que 128-127=1, que é o expoente da base binária do número obtido 2.5.3 Ponto flutuante versus inteiroPonto flutuante pode representar números muito grandes e números muito pequenos. Por exemplo, com os 32 bits da precisão simples pode-se representar a faixa de até aproximadamente . Enquanto que na representação inteira consegue-se somente a faixa até Qual o preço a pagar? A precisão dos números em ponto flutuante pode ser menor. Ex: Dado um valor inteiro de 32 bits y1 = 11111111 11111111 11111111 00000001 = 1,1111111 11111111 11111111 00000001 Ponto flutuante equivalente y2 = 1,1111111 11111111 11111111 S=0, F=1111...1, E=158 O erro relativo é dado por: (y1-y2)/y1 = (00000000 00000000 00000000 00000001)/y1 = 1/y1 que é aproximadamente Perceba que esse é o menor erro possível. Qual seria o erro aproximado para 11111111 11111111 11111111 10000000? |
| Aula 5 - 20/2/15: Aritmética binária |
|---|
2.6 Adição sem sinalEx: 1101 4 bits +1011 4 bits _____ 11000 5 bits Normalmente computadores armazenam somente N bits, ou seja, pode ocorrer overflow (estouro) como é o caso do exemplo acima com N = 4. 2.6.1 Adição sem sinal com entrada de N bits e saída de N bitsComo pode ocorrer overflow deve-se ter critérios para detecção automática caso esse caso ocorra:
Ex: 0000 1111 1000 1001 1001 1000 +0110 Certo! +0111 Errado! +1000 Errado! _____ _____ Pelos dois critérios _____ Pelo primeiro critério. 1111 0000 0000 2.6.2 Adição sem sinal com entrada de N bits e saída de N+1 bitsNunca ocorre overflow! 2.7 Adição e subtração com sinalSubtração binária 0-1-1 0 --> borrow (empresta-um) 1 0 0 1 - 0 1 1 1 _________ 0 0 0 1 0 Na prática a subtração não é utilizada. Utiliza-se complemento de dois, já que, por exemplo, a-b=a+(-b), onde "-b" é o complemento de dois de "b". 2.7.1 Adição e subtração com sinal com entradas de N bits e saída de N bitsComo pode ocorrer overflow deve-se ter critérios para detecção automática caso esse caso ocorra:
Ex: 0000 0111 1111 1000 1100 0101 0101 1011 1011 0101 +0010 Certo! +0011 Errado! +1101 Certo! +1100 Errado! +1110 Certo! _____ _____ Pelos dois critérios _____ _____ Pelos dois critérios _____ 0111 1000 1000 0111 0011 2.7.2 Adição e subtração com sinal com entradas de N bits e saída de N+1 bitsNunca ocorre overflow, MAS:
Ex: 0111 1000 0000 1111 0111 1000 0111 1001 +0111 +1000 +1000 +0111 _____ _____ _____ _____ 01110 10000 11111 00000 Regra prática: extensão do sinal em cada operando, desprezando novo overflow Ex: 00111 11000 00111 11001 +00111 +11000 +11000 +00111 _____ _____ _____ _____ 01110 10000 11111 00000 |
| Aula 6 - 25/2/15: Uso de deslocamentos nas operações aritméticas e multiplicação binária. |
|---|
2.8 Princípios da divisão e multiplicaçãoO que ocorre a uma palavra binária de N bits se a deslocarmos um bit a direita? 1100110 (102) --> 0110011 (51) 1100111 (103) --> 0110011 (51) Percebe-se que o número é dividido por 2 (base), com certo erro em alguns casos. O que ocorre a uma palavra binária de N bits se a deslocarmos um bit a esquerda? 01100110 (102) --> 11001100 (204) 1100111 (103) --> 1001110 (78) Percebe-se que o número é multiplicado por 2 (base), com erro grave em caso de overflow. 2.9 Operações de deslocamento (SHIFT)2.9.1 SHIFT lógicoA palavra binária de N bits é deslocada um certo número de posições para a direita ou para a esquerda, as posições vazias são preenchidas por zeros. SRL = shift right logical SLL = shift left logical Ex: 10111 SRL2 = 00101 10100 SRL2 = 00101 11101 SLL1 = 11010 11101 SRL-1 = 11010 2.9.2 SHIFT aritméticoO vetor binário é deslocado um certo número de posições para a direita ou para a esquerda. Quando deslocado para a direita, as posições vazias são preenchidas com o valor do bit original da estrema esquerda (bit de sinal). Quando deslocado para a esquerda, em VHDL, as posições vazias são preenchidas com o valor do bit original da estrema direita. SRA = shift right arithmetic SLA = shift left arithmetic Ex: 10101 SRA2 = 11101 10101 SLA1 = 01011 2.9.3 SHIFT circular (rotação)Semelhando ao SHIFT lógico, com a diferença que as posições vazias são preenchidas com os bits removidos. ROR = rotational right ROL = rotational left Ex: 11001 ROR2 = 01110 11001 ROL1 - 10011 2.9.4 Divisão usando SHIFT lógico para números sem sinalRegra: um deslocamento lógico de uma posição para a direita resulta na divisão do número por 2 (base), duas posições por 4 (base²)... Ex: 101110 SRL1 = 010111 110101 SRL1 = 011010 101100 SRL2 = 001011 101111 SRL2 = 001011 2.9.5 Divisão usando SHIFT aritmético para números com sinalEx: 01110 --> 00111 00111 --> 00011 10000 --> 11000 11001 --> 11100 2.9.6 Multiplicação usando SHIFT lógicoRegra: um deslocamento lógico de uma posição para a esquerda resulta na multiplicação do número por 2 Números sem sinal, ex: 01110 --> 11100 11010 --> 10100 Número com sinal, ex: 00111 --> 01110 01110 --> 11100 11000 --> 10000 10000 --> 00000 Observe que quando o par de bits iniciais for igual o resultado é correto e incorreto em caso contrário. 2.9.7 Multiplicação usando SHIFT lógico e uma saída mais largaNa prática, dobra-se o número de bits (2N) do resultado, garantindo assim a não mais ocorrência do overflow com até N deslocamentos. Números sem sinal com 4 deslocamentos, ex: 0011 (3) --> 0000 0011 (3) --> 0011 0000 (48) 1000 (8) --> 0000 1000 (8) --> 1000 0000 (128) Números com sinal com 4 deslocamentos, ex: 0011 (3) --> 0000 0011 (3) --> 0011 0000 (48) 1000 (-8) --> 1111 1000 (-8) --> 1000 0000 (-128) 1111 (-1) --> 1111 1111 (-1) --> 1111 0000 (-16) |
| Aula 7 - 27/2/15: Multiplicação e divisão binária e operações aritmética de ponto flutuante |
|---|
2.10 Multiplicação sem sinalCom N bits de entrada e 2N bits de saída não ocorre overflow. Algoritmo básico. Ex: 1101
x1100
_____
0000
0000
1101
1101
________
10011100
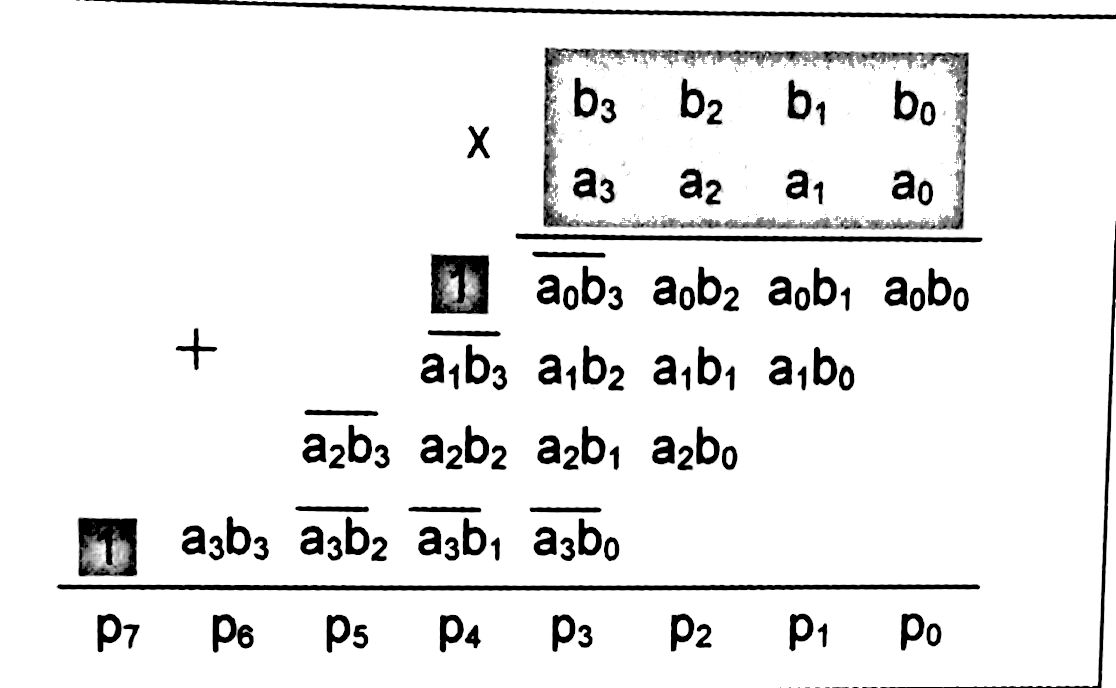
Qualquer algoritmo de multiplicação é derivado do algoritmo utilizado para a resolução do exemplo anterior. Quando faz-se uma implementação no hardware, do zero, utiliza-se esse algoritmo. Por outro lado a multiplicação pode ser efetuada usando somente operações de adição e deslocamento, abordagem empregada por exemplo em computadores, já que os mesmos possuem uma ALU que faz adições enquanto a unidade de controle pode facilmente deslocar os registradores de dados conforme a necessidade. Um exemplo de multiplicação sem sinal baseada em ALU é mostrado na figura a seguir. Multiplicação de 1001 (multiplicando) por 1100 (multiplicador): Em resumo: se o bit de produto da extrema direita for 1, o multiplicando é adicionado a metade esquerda do produto, em seguida o registrador de produto é deslocado uma posição para a direita, entretanto, se o bit for 0, deve ocorrer somente a operação de deslocamento (a multiplicação de qualquer valor por zero é igual a zero, por isso não ocorre a soma). 2.10.1 Multiplicação com sinalAlgoritmos para a multiplicação com sinal também são derivados do algoritmo básico. Na figura a seguir é ilustrado o multiplicador Baugh-Wooley modificado. Por exemplo, vamos empregar o algoritmo acima para multiplicar 1101 e 1100: padrão Baugh-Wooley 1101 1101 (-3)
x1100 x1100 (-4)
_____ _____
0000 11000
0000 --> 1000
1101 0101
1101 11010
_________ __________
00001100 (+12)
Algoritmo baseado em ALU, algoritmo de Booth. Multiplicação de 01110 (multiplicando) por 10010 (multiplicador). 5 bits nos operandos leva a necessidade de 5 iterações e 10 bits de saída: Em resumo: se os bits da extrema direita forem 10, o multiplicando deve ser subtraído da metade esquerda do registrador de produto e o resultado deve ser deslocado aritmeticamente para a direita. Se os bits forem 01 então o multiplicando deve ser somado à metade esquerda do registrador de produto e o resultado deslocado aritmeticamente para a direita. Por fim, se os bits forem 00 ou 11, então deve ocorrer somente o deslocamento aritmético para a direita. 2.10.2 Divisão sem sinalAlgoritmo básico, 1101 (13) dividido por 0101 (5): decimal (para relembrar :) ) binário
dividendo --> 173 |_7 <--divisor 0001101 |_0101
00 024 <-- quociente 0000 0010 <-- quociente
__ ____
17 0011
14 0000
__ ____
033 0110
28 0101
__ ____
05 <-- resto 0011 <-- resto
Obs:
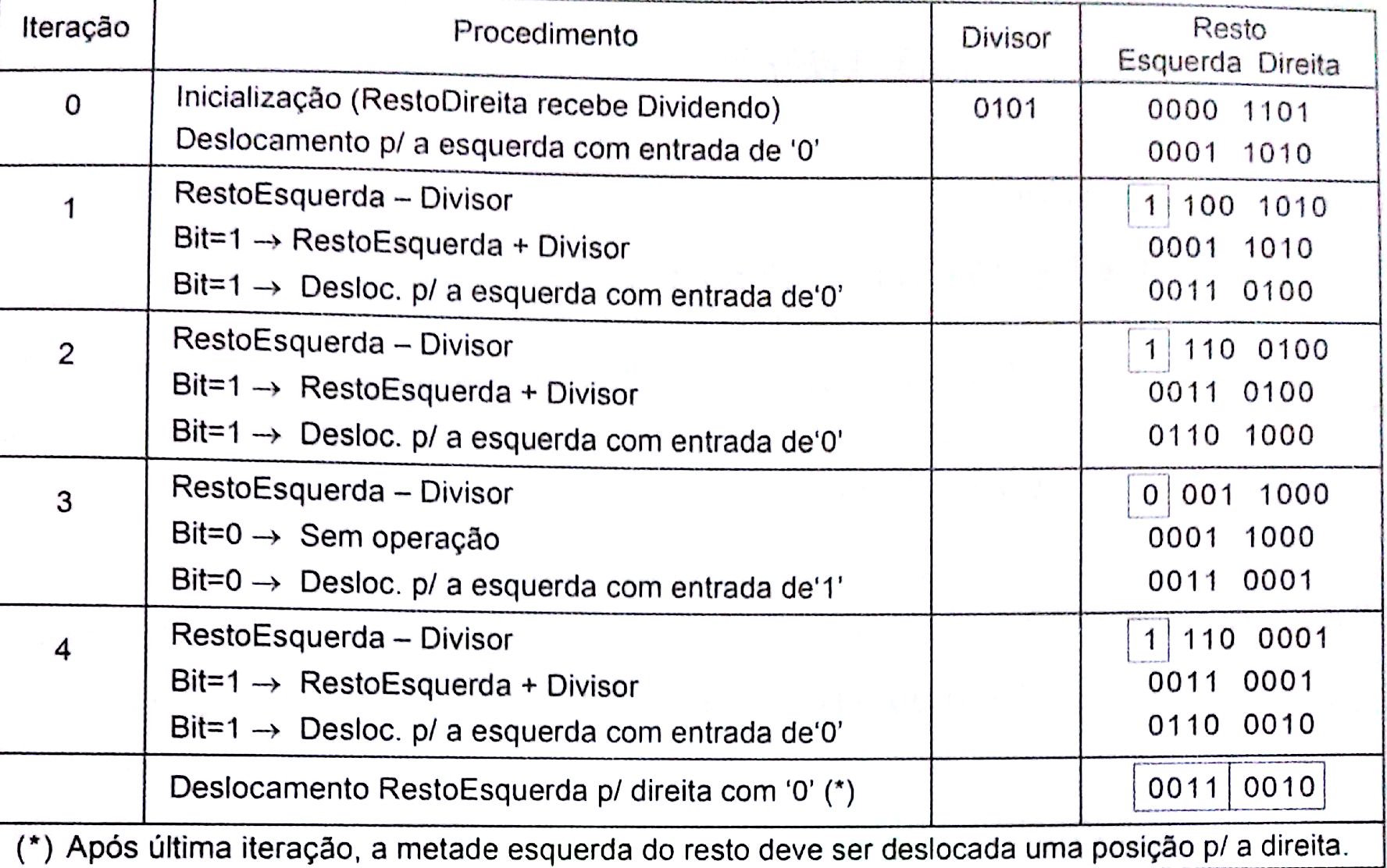
Do ponto de vista de hardware, é mais difícil implementar divisões dedicadas do que multiplicadores dedicados. Por essa razão, a abordagem mais comum é empregar algoritmos baseados em ALU para a divisão, os quais utilização operações de adição, subtração e deslocamento. Um algoritmo desse tipo é mostrado na figura a seguir, onde 1101 (13) é dividido por 0101 (5). Deve-se ter N iterações para a solução e o registrador de resto deve ter 2N bits. Em resumo: o divisor é subtraído da metade esquerda do resto, se o resultado for negativo, o divisor é somado de volta ao resto, restaurando seu valor, e então é realizado um shift para a esquerda e a posição vazia é preenchida com um zero. Ao contrário, se o resultado for positivo, o registrador de resto é deslocado para a esquerda e a posição vazia é preenchida com um 1. Após a última iteração, a metade esquerda do registrador de resto deve ser deslocada para a direita e a posição vazia preenchida com um zero. O quociente aparecerá na metade direita do registrador de resto, enquanto o resto verdadeiro aparecerá em sua metade esquerda. 2.10.3 Divisão com sinalA divisão com sinal é normalmente efetuada como se os números não tivessem sinal. Isso implica que, em primeiro lugar, os números negativos devem passar por complemento de dois. Além disso, se o dividendo e o divisor tiverem sinais diferentes, então o quociente deve ser negativado (complemento de dois) e o resto também. Ex: 1001 (-7) / 0011 (+3) Complemento de dois de 1001 é 0111
0000111 |_ 0011
0000 0010 <-- quociente
____
0001
0000
____
0011
0011
____
0001 <-- resto
complemento de dois de 0010 é 1110 (-2)
complemento de dois de 0001 é 1111 (-1)
2.10.4 Operações com ponto flutuanteVer seções 3.8, 3.9 e 3.10 do livro do Pedroni. |
| Aula 8 - 4/3/15: Laboratório 1 |
|---|
|
| Aula 9 - 6/3/15: Portas NOT, AND, NAND, OR, NOR |
|---|
|
Seções 4.1 a 4.4 do livro texto. |
| Aula 10 - 11/3/15: Laboratório 2 |
|---|
|
Continuação e complementação do laboratório 1. No primeiro laboratório foi focado o uso do Quartus (interface), inserção do projeto (schematic), análise do RTL, e o início da simulação funcional (QSIM). Hoje vamos gravar e utilizar o Kit Mercurio IV (Family=Cyclone IV E / device=EP4CE30F23C7) seguindo o roteiro:Preparando para gravar o circuito lógico no FPGA 2.10.5 Procedimento para salvar e recuperar projetos
|
| 13/3/15: Aula cancelada por licença médica |
|---|
| Aula 11 - 18/3/15: Avaliação 1 - 7h30 sala 12 |
|---|
| Aula 12 - 20/3/15: Portas OR, NOR, XOR, Buffer, Tri-state |
|---|
|
Seções 4.4, 4.5, 4.7 e 4.8 do livro texto. |
| Aula 14 - 27/3/15: Algebra de Boole. Mintermos, Maxtermos, Equações SOP e POS |
|---|
|
Seções 5.3, 5.4 e 5.5 do livro texto. |
| Aula 15 - 1/4/15: Algebra de Boole. Mintermos, Maxtermos, Equações SOP e POS |
|---|
|
Seções 5.3, 5.4 e 5.5 do livro texto. |
| Aula 16 - 8/4/15: Mapas de Karnaugh |
|---|
|
Seções 5.6 e 5.7 do livro texto. |
| Aula 17 - 10/4/15: Mapas de Karnaugh e projeto de conversor BCD para SSD |
|---|
|
Seções 5.6, 5.7 e 11.5.5 do livro texto. |
| Aula 18 - 15/4/15: Laboratório conversor BCD para SSD |
|---|
|
Projete e implemente na FPGA um conversor BCD (Binary to Coded Decimal) para SSD (Seven Segment Display) que apresente a seguinte sequência de caracteres: 0, 1, ..., 9, X, X, C, X, E, X. Experimento_5_para_Circuitos_Lógicos. |
| Aula 19 - 17/4/15: Circuitos Combinacionais Lógicos -- Codificadores e Decodificadores |
|---|
|
Seções 11.1 , 11.2, 11.3, 11.4 e 11.5 do livro texto. |
| Aula 20 - 20/4/15: Circuitos Combinacionais Lógicos -- Codificadores, Decodificadores e Multiplexadores |
|---|
|
Seções 11.5 e 11.6 do livro texto. |
| Aula 21 - 24/4/15: Circuitos Combinacionais Lógicos -- Detector de paridade, portas com histerese e dúvidas para a segunda avaliação |
|---|
|
Seções 11.7 e 11.13 do livro texto. |
| Aula 22 - 27/4/15: Avaliação 2 - Circuitos Digitais e Álgebra Booleana |
|---|
| Aula 23 - 6/5/15: Cap 12 - Circuitos Combinacionais Aritméticos |
|---|
| Aula 24 - 8/5/15: Cap 12 - Circuitos Combinacionais Aritméticos |
|---|
| Aula 25 - 13/5/15: Laboratório 4 – Circuitos Aritméticos (Somador, Complemento de 2 e Subtrator) |
|---|
| Aula 26 - 15/5/15: Correção da avaliação 2 |
|---|
| Aula 27 - 19/5/15: Cap 12 - Latches, FlipFlops e Registradores |
|---|
| Aula 28 - 22/5/15: Cap 14 - Registradores e Contadores |
|---|
| Aula 29 - 27/5/15: Laboratório 5 - Circuito de Multiplicação Binária |
|---|
| Aula 30 - 29/5/15: Cap 14 - Contadores |
|---|
| Aula 31 - 3/6/15: Cap 14 - Divisor de frequência |
|---|
| Aula 32 - 10/6/15: Projeto final em equipes: Definição das equipes e especificação do projeto |
|---|
|
Projetos_Finais_CIL29003 Resultado esperado na primeira aula:
2.11 Equipes
|
| Aula 33 - 12/6/15: Terceira avaliação |
|---|
| Aula 34 - 17/6/15: Projeto final em equipes: ... |
|---|
| Aula 35 - 19/6/15: Projeto final em equipes: ... |
|---|
| Aula 36 - 24/6/15: Projeto final em equipes: ... |
|---|
| Aula 37 - 26/6/15: Projeto final em equipes: Avaliação |
|---|
| Aula 38 - 1/7/15: Projeto final em equipes: Avaliação |
|---|
| Aula 39 - 3/7/15: Reavaliação final |
|---|