Mudanças entre as edições de "PSD29007-Engtelecom(2019-2) - Prof. Marcos Moecke"

De MediaWiki do Campus São José
Ir para navegação Ir para pesquisar
Linha 306: Linha 306:
 
* A situação pode ser muito diferente conforme muda o tamanho do sinal e ordem do filtro (h(n)). Modifique a resposta ao impulso e o sinal de entrada modificando os valores das variáveis de tamanho:  Nh = 10, 100, 1000; Nx = 20, 1000, 10000;
 
* A situação pode ser muito diferente conforme muda o tamanho do sinal e ordem do filtro (h(n)). Modifique a resposta ao impulso e o sinal de entrada modificando os valores das variáveis de tamanho:  Nh = 10, 100, 1000; Nx = 20, 1000, 10000;
 
* Em função do sistema operacional e reserva de memória para as variáveis é importante desprezar a primeira medida de tempo.  Realize 3 medidas de tempo para cada uma das 5 opções de filtragem, com pelo menos duas combinações de comprimento Nh e Nx. Relate os resultados obtidos no comentário da atividade no Moodle.
 
* Em função do sistema operacional e reserva de memória para as variáveis é importante desprezar a primeira medida de tempo.  Realize 3 medidas de tempo para cada uma das 5 opções de filtragem, com pelo menos duas combinações de comprimento Nh e Nx. Relate os resultados obtidos no comentário da atividade no Moodle.
−
 
  
 
;Aula 7 (19 ago):
 
;Aula 7 (19 ago):
Linha 362: Linha 361:
 
:* Consulte a documentação do Matlab sobre [https://www.mathworks.com/help/matlab/ref/text.html text], [http://www.mathworks.com/help/signal/ref/zp2tf.html zp2tf], [http://www.mathworks.com/help/signal/ref/tf2zp.html tf2zp], [http://www.mathworks.com/help/signal/ref/fftfilt.html fftfilt], [http://www.mathworks.com/help/matlab/ref/awgn.html awgn]  
 
:* Consulte a documentação do Matlab sobre [https://www.mathworks.com/help/matlab/ref/text.html text], [http://www.mathworks.com/help/signal/ref/zp2tf.html zp2tf], [http://www.mathworks.com/help/signal/ref/tf2zp.html tf2zp], [http://www.mathworks.com/help/signal/ref/fftfilt.html fftfilt], [http://www.mathworks.com/help/matlab/ref/awgn.html awgn]  
 
:*Ver pag. 141 a 145 e 230 a 235 de <ref name="DINIZ2014"/>
 
:*Ver pag. 141 a 145 e 230 a 235 de <ref name="DINIZ2014"/>
 +
{{collapse bottom}}
 +
 +
===Unidade 2===
 +
{{collapse top |expand=true |  Unidade 2}}
 +
;Aula 8 (22 ago):
 +
*Filtros Analógicos:
 +
:* Função de transferência
 +
::<math> H(s) = \frac {c_0 + c_1 s + c_2 s^2 + ... + c_m s^m} {d_0 + d_1 s + d_2 s^2 + ... + d_n s^n}, m \le n</math>
 +
 +
:* Resposta em frequência: para obter a resposta em frequência é necessário avaliar
 +
::<math>H(j\omega) = H(s)\left|\begin{matrix}\\ s=j\omega \end{matrix}\right.</math>
 +
 +
::<math> H(j \omega) = \left | H(j \omega) \right | e^{j \phi(\omega)}</math>
 +
 +
::<math> \left | H(j \omega) \right |^2 =  H(j \omega)  H(-j \omega)</math>
 +
 +
::<math> e^{j 2 \phi(\omega)} =  \frac {H(j \omega)}  {H(-j \omega)}</math>
 +
:* O projeto de filtros analógicos é realizado em 2 etapas:
 +
# projeto de um filtro passa baixas (LP) protótipo normalizado <math> H(p) </math> com frequência de passagem <math> \Omega_s = 1 </math>
 +
# transformação em frequência para o tipo de filtro (LP, HP, BP ou BS)
 +
::<math> H(s) = H(p)\left|\begin{matrix}\\ p=g(s) \end{matrix}\right. </math>
 +
 +
* Análise básica de filtros analógicos com Matlab.
 +
:Dado um sistema linear invariante no tempo, representado pela função de transferência <math> H(s) </math>, obter a resposta de frequência do sistema (Magnitude e Fase).
 +
::<math> H(s) = \frac {s + 1} {s^2 +  s + 5} </math>
 +
::<math> H(j\omega) = \frac {s + 1} {s^2 +  s + 5}\left|\begin{matrix}\\ s=j\omega \end{matrix}\right.</math>
 +
::<math>  H(j\omega) = \frac{1 + w\, \mathrm{i}}{ - w^2 + w\, \mathrm{i} + 5} </math>
 +
 +
<syntaxhighlight lang=matlab>
 +
b = [1 1];
 +
a = [1 1 5];
 +
[z1,p1,k]=tf2zp(b,a)
 +
z2 = roots(b);
 +
p2 = roots(a);
 +
zplane(b,a);
 +
%%
 +
freqs(b,a);
 +
%%
 +
syms s  w
 +
H(s) = (s+1)/(s^2 + s + 5);
 +
pretty(H(1j*w))
 +
latex(H(1j*w))
 +
%%
 +
ws = logspace(-2, 1, 1000);
 +
h = H(1j*ws);
 +
subplot(211)
 +
semilogx(ws,abs(h)); grid on;
 +
subplot(212)
 +
semilogx(ws,angle(h)/pi*180); grid on;
 +
</syntaxhighlight>
 +
 +
* Projeto de filtros analógicos do tipo Butterworth
 +
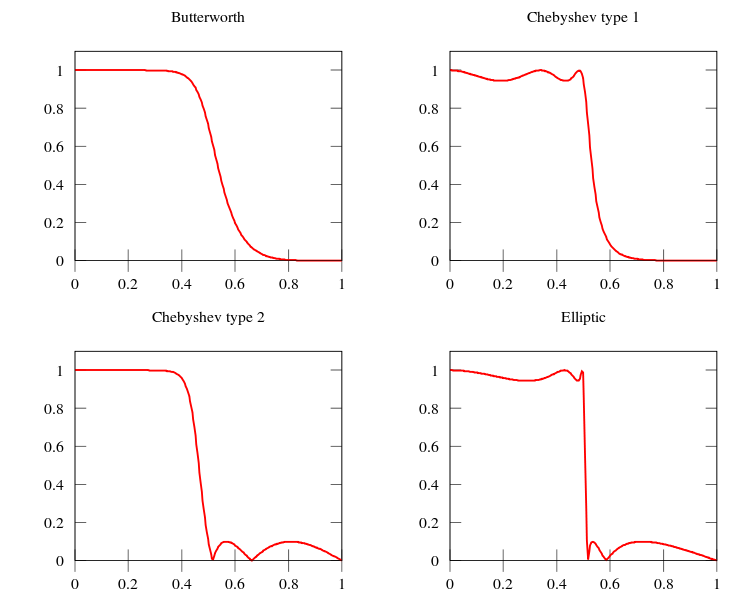
:* A aproximação de magnitude de filtros analógicos pode ser realizado usando as aproximações de Butterworth, Chebyshev (tipo 1 ou 2) e Cauer.
 +
 +
[[Arquivo:TiposFiltrosHs.png | 600px]]
 +
 +
;Proposta de exercício:
 +
*Use os polinômios de Butterworth com ordens de 1 a 10 mostrados na tabela abaixo para obter os filtros <math>H_n(s) = 1/B_n(s)</math>.
 +
 +
{|
 +
|-----
 +
|
 +
{| class="wikitable" style="text-align: center;"
 +
|-
 +
!n!!Fatores Polinomiais de <math>B_n(s)</math>
 +
|-
 +
!1
 +
|<math>(s+1)</math>
 +
|-
 +
!2
 +
|<math>(s^2+1.4142s+1)</math>
 +
|-
 +
!3
 +
|<math>(s+1)(s^2+s+1)</math>
 +
|-
 +
!4
 +
|<math>(s^2+0.7654s+1)(s^2+1.8478s+1)</math>
 +
|-
 +
!5
 +
|<math>(s+1)(s^2+0.6180s+1)(s^2+1.6180s+1)</math>
 +
|-
 +
!6
 +
|<math>(s^2+0.5176s+1)(s^2+1.4142s+1)(s^2+1.9319s+1)</math>
 +
|-
 +
!7
 +
|<math>(s+1)(s^2+0.4450s+1)(s^2+1.2470s+1)(s^2+1.8019s+1)</math>
 +
|-
 +
!8
 +
|<math>(s^2+0.3902s+1)(s^2+1.1111s+1)(s^2+1.6629s+1)(s^2+1.9616s+1)</math>
 +
|-
 +
!9
 +
|<math>(s+1)(s^2+0.3473s+1)(s^2+s+1)(s^2+1.5321s+1)(s^2+1.879s+1)</math>
 +
|-
 +
!10
 +
|<math>(s^2+0.3129s+1)(s^2+0.9080s+1)(s^2+1.4142s+1)(s^2+1.7820s+1)(s^2+1.9754s+1)</math>
 +
|}
 +
|}
 +
*Escolha uma ordem n (entre 5 e 10)
 +
*Plote a resposta em frequência em escala log da amplitude (em dB) e da fase (em rad/pi). 
 +
*Qual é o ganho do filtro na banda passante?
 +
*Qual é a frequência de corte (-3dB) do filtro.
 +
*Qual é o salto de de fase que ocorre em algumas frequências?
 +
*Qual é o fator de atenuação em dB/decada após a frequência de corte?
 +
 +
*Faça o diagrama de polos e zeros desse filtro.
 +
*Procure observar o que ocorre com a posição dos polos do filtro.
 +
*Calcule o valor do módulo dos pólos.
 +
 +
<!--
 +
;Aula 7, 8 (8, 13 mar):
 +
 +
* Projeto de filtros analógicos passa baixas (low pass - LP) do tipo Butterworth, considerando: <math> \omega_p </math> é a frequência de passagem, <math> A_p = 3 dB </math> é a atenuação em dB na frequência de passagem, <math> \omega_s </math> é a frequência de ''stopband'', <math> A_s </math> é a atenuação em dB na frequência de ''stopband''.
 +
[[Arquivo:MascaraFiltroLP.png | 600px]]
 +
 +
*Escalando as frequências em relação a  <math> {\omega_p} </math>, teremos que <math> \Omega_s = \frac {\omega_s} {\omega_p} </math>, e <math> \Omega_p = \frac {\omega_p} {\omega_p} = 1 </math> são as frequências de passagem e ''stopband'' do filtro protótipo <math> H(p) </math>, que tem ganho unitário e frequência de passagem 1.
 +
 +
;<math> A_p = 3 dB </math>:
 +
*Se considerarmos o caso particular em que na frequência de passagem o ganho (em escala linear) deve ser <math> G_p = 1/\sqrt{2} = 0,707 </math>, que corresponde a um ganho (em escala log) <math> G_p = - 3 dB </math>, ou atenuação <math> A_p = 3 dB </math>.
 +
*Considere que <math> \epsilon = \sqrt{10^{0.1A_p}-1}</math>, teremos <math> \epsilon = 1 </math>
 +
*Para projetar o filtro é necessário:
 +
 +
:1) determinar a ordem <math> n </math> do filtro: 
 +
 +
::<math> n \ge \frac {\log(10^{0.1A_s}-1)} {2 \log \Omega_s} </math>
 +
 +
:2) obter os polos do filtro:
 +
 +
::<math> p_k = e^{\left[ j \frac{(2 k + n - 1)} {2 n} \pi \right]},  k = 1, 2, 3, ... n</math>
 +
 +
:3) obter a função de transferência:
 +
 +
::<math> H(p)= \frac{1}{D(p)} </math>, onde <math> D(p)=\prod_{k-1}^{n} \left ( p-p_{k} \right ) </math>
  
 +
::* No caso de um filtro LP é necessário ainda obter a função de transferência do filtro especificado fazendo a transformação de frequência <math> H(p) -> H(s) </math>
 +
 +
::<math>H(s) = H(p)\left|\begin{matrix} \\ p=\frac{s}{\omega_p} \end{matrix}\right. </math>
 +
 +
 +
;Para qualquer <math> A_p </math>:
 +
*Teremos <math> \epsilon = \sqrt{10^{0.1A_p}-1}</math>
 +
 +
*Para projetar o filtro é necessário:
 +
:1) determinar a ordem <math> n </math> do filtro: 
 +
 +
::<math> n \ge \frac {\log[(10^{0.1A_s}-1)/\epsilon^2]} {2 \log \Omega_s} </math>
 +
 +
:2) obter os polos do filtro:
 +
 +
::<math> p_k = \epsilon^{(-1/n)} e^{\left[ j \frac{(2 k + n - 1)} {2 n} \pi \right]},  k = 1, 2, 3, ... n</math>
 +
 +
:3) obter a função de transferência:
 +
 +
::<math> H(p)= \frac{k}{D(p)} </math>, onde <math> k=\prod_{k-1}^{n} \left (-p_{k} \right ) =  \epsilon^{-1}</math> e <math> D(p)=\prod_{k-1}^{n} \left ( p-p_{k} \right ) </math>.
 +
::NOTA: o valor <math> k </math> também pode ser obtido a partir de <math> {D(p)} </math>, pois corresponde ao último termo do polinômio <math> {D(end)} </math>.
 +
 +
::* No caso de um filtro LP é necessário ainda obter a função de transferência do filtro especificado fazendo a transformação de frequência <math> H(p) -> H(s) </math>
 +
::<math>H(s) = H(p)\left|\begin{matrix} \\ p=\frac{s}{\omega_p} \end{matrix}\right. </math>
 +
 +
:*Ver [[Uso do calculo simbólico na Matlab]]
 +
:*Ver pag. 186 a 204 de <ref name="SHENOI2006"> SHENOI, B. A. '''Introduction to Digital Signal Processing and Filter Design'''. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822 </ref>
 +
 +
<!--
 +
<syntaxhighlight lang=matlab>
 +
%Butterworth lowpass Responses (db)
 +
w = 0.1:0.01:10;
 +
H=inline('10*log10(1./(1+w.^(2*n)))','w','n');
 +
for k = 1:1:10
 +
    semilogx(w,H(w,k)); hold on;
 +
end
 +
grid on
 +
 +
%Butterworth lowpass Responses (linear)
 +
w = 0.1:0.01:2;
 +
H=inline('1./(1+w.^(2*n))','w','n');
 +
for k = 1:1:10
 +
    plot(w,H(w,k)); hold on;
 +
end
 +
grid on
 +
</syntaxhighlight>
 +
-->
 +
 +
<!--
 +
;Aula 9 e 10 (15 e 20 mar):
 +
* Projeto de filtros analógicos do tipo Chebyshev I.
 +
:* Polinômios de Chebyshev:
 +
Os polinômios de Chebyshev de primeira ordem são definidos pela relação recursiva:
 +
:<math>C_0(\Omega) = 1 \,\!</math>
 +
:<math>C_1(\Omega) = \Omega \,\!</math>
 +
:<math>C_{n}(\Omega) = 2 \times C_{n-1}(\Omega) - C_{n-2}(\Omega). \,\!</math>
 +
 +
Os primeiros cinco polinômios de Chebyshev de primeira ordem são:
 +
:<math> C_0(\Omega) = 1 \,</math>
 +
:<math> C_1(\Omega) = \Omega \,</math>
 +
:<math> C_2(\Omega) = 2\Omega^2 - 1 \,</math>
 +
:<math> C_3(\Omega) = 4\Omega^3 - 3\Omega \,</math>
 +
:<math> C_4(\Omega) = 8\Omega^4 - 8\Omega^2 + 1 \,</math>
 +
:<math> C_5(\Omega) = 16\Omega^5 - 20\Omega^3 + 5\Omega \,</math>
 +
 +
::*Determine a ordem mínima necessária considerando: <math> \omega_p </math> é a frequência de passagem do filtro LP, <math> A_p </math> é a atenuação em dB na frequência de passagem, <math> \omega_s </math> é a frequência de ''stopband'' do filtro, <math> A_s </math> é a atenuação em dB na frequência de ''stopband'', <math> \epsilon = \sqrt{10^{0.1A_p}-1 } </math>, <math> \Omega_s = \frac {\omega_s} {\omega_p} </math>, <math> \Omega_p = \frac {\omega_p} {\omega_p} = 1 </math> são as frequências de passagem e ''stopband'' do filtro protótipo.
 +
::<math> n \ge \frac {\cosh^{-1} \sqrt{(10^{0.1A_s}-1)/(10^{0.1A_p}-1)}} {\cosh^{-1} \Omega_s} </math>
 +
 +
::*Em seguida obter os polos do filtro:
 +
 +
::<math> p_k = -\sinh(\varphi_2) \sin(\theta_k)+ j \cosh(\varphi_2) \cos(\theta_k) \ \ \ \ \  k = 1, 2, 3, ... n</math>, onde
 +
::<math> \theta_k = \left ( \frac{(2k-1)\pi}{2n} \right ) </math>
 +
::<math> \varphi_2 =  \frac{1}{n} \sinh^{-1}\left (\frac{1}{\epsilon}  \right ) </math>
 +
 +
:<math>\left | H( j\Omega ) \right | ^2 =  1 \text{para n impar}, \frac {1}{1+\epsilon^2} \text{para n par} </math>
 +
 +
:<math>\left | H(0) \right | ^2 = \frac{H_0^2}{ 1+ \epsilon^2 C_n ^2 \left ( \Omega_0 \right )} </math>
 +
 +
::* Para obter a função de transferência:
 +
 +
::<math> H(p)= \frac{H0}{D(p)} </math>, onde <math> D(p)=\prod_{k-1}^{n} \left ( p-p_{k} \right ) </math>
 +
::onde
 +
::<math> H_0 = d_0*\sqrt{\frac{1}{ 1+ \epsilon^2}} </math> se n  é par
 +
::<math> H_0 = d_0 </math> se n  é impar
 +
::<math> d_0 =\prod_{k-1}^{n} \left (-p_{k} \right ) </math> é o último termo do denominador D(p)
 +
 +
:* Uso das funções [http://www.mathworks.com/help/signal/ref/buttord.html buttord], [http://www.mathworks.com/help/signal/ref/butter.html butter], [http://www.mathworks.com/help/signal/ref/cheb1ord.html cheb1ord], [http://www.mathworks.com/help/signal/ref/cheby1.html cheby1],  [http://www.mathworks.com/help/signal/ref/cheb2ord.html cheb2ord], [http://www.mathworks.com/help/signal/ref/cheby2.html cheby2], [http://www.mathworks.com/help/signal/ref/ellipord.html ellipord], [http://www.mathworks.com/help/signal/ref/ellip.html ellip] para o projeto de filtros analógicos com Matlab (é necessário usar o parâmetro ''''s'''').
 +
:* Ler '''Comparison of Analog IIR Lowpass Filters''' em [http://www.mathworks.com/help/signal/ref/ellip.html ellip]
 +
:* Uso das funções [http://www.mathworks.com/help/signal/ref/freqs.html freqs], "zplane", [http://www.mathworks.com/help/signal/ref/fvtool.html fvtool] na análise da resposta em frequência de filtros analógicos.
 +
 +
* Projeto de filtros analógicos do tipo Butterworth, Chebyshev I e II e Cauer (eliptico) usando funções do Matlab.
 +
<syntaxhighlight lang=matlab>
 +
%% Projeto de filtro passa-baixas usando funções do Matlab 
 +
%% Especificações do filtro
 +
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
 +
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
 +
 +
%% Butterworth
 +
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
 +
[b,a] = butter(n,Wn, 's');
 +
 +
%% Chebyshev I
 +
n = cheb1ord(Wp, Ws, Ap, As,'s')
 +
[b,a] = cheby1(n,Ap, Wp, 's');
 +
 +
%% Chebyshev II
 +
n = cheb2ord(Wp, Ws, Ap, As,'s')
 +
[b,a] = cheby2(n,As, Ws, 's');
 +
 +
%% Elliptic - Cauer
 +
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
 +
[b,a] = ellip(n,Ap,As, Wn, 's');
 +
</syntaxhighlight>
 +
:*Ver pag. 204 a 208 de <ref name="SHENOI2006"/>
 +
 +
 +
;Aula 11 a 13 (22,27, 29  mar):
 +
*Filtros Analógicos:
 +
:* Transformações de frequência de filtros analógicos 
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-baixas (<math> \omega_p</math>)
 +
::*Substituição de variáveis <math> p = \frac{s}{\omega_p}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \frac{\omega_s}{\omega_p}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-altas (<math> \omega_p</math>)
 +
::*Substituição de variáveis <math> p = \frac{\omega_p} {s}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \frac{\omega_p}{\omega_s}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-faixa (<math> \omega_0 </math> e <math> B </math>)
 +
::*Substituição de variáveis <math> p = \frac{s^2 + \omega_0^2} {B s}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \Bigg|\frac{-\omega_s^2 + \omega_0^2} {B \omega_s}\Bigg|</math>
 +
:: onde <math> B = \omega_{p2} - \omega_{p1}</math>  e <math> \omega_0 = \sqrt{\omega_{p2} \omega_{p1}}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> rejeita-faixa (<math> \omega_0 </math> e <math> B </math>)
 +
::*Substituição de variáveis <math> p = \frac {B s} {s^2 + \omega_0^2}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \Bigg| \frac {B \omega_s} {-\omega_s^2 + \omega_0^2}\Bigg|</math>
 +
:: onde <math> B = \omega_{p2} - \omega_{p1}</math>  e <math> \omega_0 = \sqrt{\omega_{p2} \omega_{p1}}</math>
 +
 +
:* Uso das funções [http://www.mathworks.com/help/matlab/ref/semilogx.html semilogx], [http://www.mathworks.com/help/matlab/ref/semilogy.html semilogy],[http://www.mathworks.com/help/matlab/ref/logspace.html logspace], [http://www.mathworks.com/help/matlab/ref/linspace.html linspace].
 +
:*Ver em [http://www.mathworks.com/help/signal/ug/iir-filter-design.html IIR Filter Design], [http://www.mathworks.com/help/signal/ug/special-topics-in-iir-filter-design.html Special Topics in IIR Filter Design].
 +
::*Funções para projeto do filtro protótipo analógico passa-baixas: [http://www.mathworks.com/help/signal/ref/buttap.html buttap], [http://www.mathworks.com/help/signal/ref/cheb1ap.html cheb1ap], [http://www.mathworks.com/help/signal/ref/cheb2ap.html cheb2ap], [http://www.mathworks.com/help/signal/ref/ellipap.html ellipap]
 +
::*Funções de transformação de frequencia: [http://www.mathworks.com/help/signal/ref/lp2lp.html lp2bp], [http://www.mathworks.com/help/signal/ref/lp2hp.html lp2bs], lp2hp, lp2lp
 +
:*Ver pag. 208 a 218 de <ref name="SHENOI2006"/>
 +
 +
*Exemplos de Filtros Analógicos:
 +
:* Exemplo 1: Filtro passa-baixas (<math> f_p </math> = 941Hz, <math> f_s </math> = 1209 Hz, <math> A_p </math> = 1 dB, <math> A_s </math> = 20 dB)
 +
:* Exemplo 2: Filtro passa-altas (<math> f_p </math> = 1209 Hz, <math> f_s </math> = 941Hz, <math> A_p </math> = 1 dB, <math> A_s </math> = 20 dB)
 +
:* Exemplo 3: Filtro passa-faixa (<math> f_{p1} </math> = 811 Hz, <math> f_{p2} </math> = 895,5 Hz <math> f_{s1} </math> = 770 Hz, <math> f_{s2} </math> = 941 Hz, <math> A_p </math> = 1 dB, <math> A_r </math> = 30 dB)
 +
:* Exemplo 5: Filtro rejeita-faixa (<math> f_{p1} </math> = 53 Hz, <math> f_{s1} </math> = 58 Hz, <math> f_{s2} </math> = 62 Hz  <math> f_{p2} </math> = 67 Hz, <math> A_p </math> = 2 dB, <math> A_r </math> = 25 dB)
 +
::'''NOTA:'''
 +
:::*No calculo do filtro lembre-se de usar as frequências angulares para <math> \omega_p </math>, <math> \omega_s </math>, <math> B\omega </math>, <math> \omega_0 </math>.
 +
:::*onde <math> f_p </math> (<math> \omega_p </math>) é a frequência de passagem em Hz (rad/s), <math> f_s </math> (<math> \omega_s </math>) é a frequência de rejeição em Hz (rad/s), <math> f_0 </math> (<math> \omega_0 </math>) é a frequência central em Hz (rad/s), <math> B </math> (<math> B\omega </math>) é a largura de banda  em Hz (rad/s).
 +
:::*Confira os projetos dos filtros plotando as respostas em frequência dos filtros protótipo H(p) e filtro final H(s) de cada um dos exemplos.
 +
 +
 +
;Aula 14 e 15 (3 e 5 abr):
 +
*Filtros Digitais:  Filtros IIR: transformações do tempo contínuo no tempo discreto
 +
:*Transformação invariante ao impulso  (pode ser usada apenas para filtros com forte atenuação em frequência altas, ex: passa-baixas e passa-faixa)
 +
:*Transformação bilinear (pode ser usada para todos tipos de filtro) <math> s = 2fa \frac {z-1}{z+1} </math>
 +
::*Obter a especificação do filtro em angulo entre 0 e 1, onde 1 corresponde a metade da frequência de amostragem  <math> (fa/2) </math>
 +
::*Obter o valor desse angulo predistorcido <math> \lambda  </math> para compensar a distorção na frequência causada pela transformação bilinear <math> \lambda= 2 tan \left (\frac{\theta \pi}{2} \right ) </math>, onde <math> \theta = \frac{f}{f_a/2} = \frac{\omega}{\omega_a /2} </math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-baixas (<math> \lambda_p</math>)
 +
::*Substituição de variáveis <math> p = \frac{s}{\lambda_p}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \frac{\lambda_s}{\lambda_p}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-altas (<math> \lambda_p</math>)
 +
::*Substituição de variáveis <math> p = \frac{\lambda_p} {s}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \frac{\lambda_p}{\lambda_s}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> passa-faixa (<math> \lambda_0 </math> e <math> B </math>)
 +
::*Substituição de variáveis <math> p = \frac{s^2 + \lambda_0^2} {B s}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \Bigg|\frac{-\lambda_s^2 + \lambda_0^2} {B \lambda_s}\Bigg|</math>
 +
:: onde <math> B = \lambda_{p2} - \lambda_{p1}</math>  e <math> \lambda_0 = \sqrt{\lambda_{p2} \lambda_{p1}}</math>
 +
 +
:*passa-baixas (<math> \Omega_p= 1 </math>) -> rejeita-faixa (<math> \lambda_0 </math> e <math> B </math>)
 +
::*Substituição de variáveis <math> p = \frac {B s} {s^2 + \lambda_0^2}</math>
 +
::*Cálculo do protótipo com <math> \Omega_s = \Bigg| \frac {B \lambda_s} {-\lambda_s^2 + \lambda_0^2}\Bigg|</math>
 +
:: onde <math> B = \lambda_{p2} - \lambda_{p1}</math>  e <math> \lambda_0 = \sqrt{\lambda_{p2} \lambda_{p1}}</math>
 +
::*Ver as funções de discretização usadas no Matlab: [http://www.mathworks.com/help/signal/ref/bilinear.html bilinear], [http://www.mathworks.com/help/signal/ref/impinvar.html impinvar]
 +
 +
* Realizar os projetos dos exemplos anteriores, considerando uma frequencia de amostragem de 8 kHz.
 +
 +
:*Ver pag. 219 a 229 de <ref name="SHENOI2006"/>
 +
:*Ver pag. 403 a 415 e 434 a 435 de <ref name="DINIZ2014"/>
 +
;Aula 16 (10 abr):
 +
 +
:* Ver em [http://www.mathworks.com/help/signal/ug/iir-filter-design.html IIR Filter Design]
 +
:* Uso das funções [http://www.mathworks.com/help/signal/ref/buttord.html buttord], [http://www.mathworks.com/help/signal/ref/butter.html butter], [http://www.mathworks.com/help/signal/ref/cheb1ord.html cheb1ord], [http://www.mathworks.com/help/signal/ref/cheby1.html cheby1],  [http://www.mathworks.com/help/signal/ref/cheb2ord.html cheb2ord], [http://www.mathworks.com/help/signal/ref/cheby2.html cheby2], [http://www.mathworks.com/help/signal/ref/ellipord.html ellipord], [http://www.mathworks.com/help/signal/ref/ellip.html ellip] para o projeto de filtros IIR digitais (sem o parâmetro ''''s'''').
 +
::O projeto dos filtros digitais IIR baseados na transformada bilinear no Matlab é realizada em dois passos:  (1)  Determinação da ordem do filtro; (2) Determinação dos coeficientes do numerador <math> b(n) </math> e denominador  <math> a(n) </math> de <math> H(z) </math> .
 +
 +
:* Outros tipos de filtros IIR:  [http://www.mathworks.com/help/signal/ref/yulewalk.html yulewalk], [https://www.mathworks.com/help/dsp/ref/iirnotch.html iirnotch], [https://www.mathworks.com/help/dsp/ref/iirpeak.html iirpeak], [https://www.mathworks.com/help/dsp/ref/iircomb.html iircomb],[http://www.mathworks.com/help/signal/ref/filtfilt.html filtfilt], [http://www.mathworks.com/help/signal/ref/maxflat.html maxflat], [http://www.mathworks.com/help/signal/ref/invfreqz.html invfreqz] e outros filtros de [http://www.mathworks.com/help/signal/ug/parametric-modeling.html modelagem paramétrica].
 +
 +
<syntaxhighlight lang=matlab>
 +
fa = 200;
 +
fN = fa/2;
 +
wo = 60/fN;  bw = 10/fN;
 +
[b,a] = iirnotch(wo,bw);
 +
fvtool(b,a);
 +
syms z;
 +
N(z) = poly2sym(b,z);
 +
D(z) = poly2sym(a,z);
 +
H(z) = N(z)/D(z);
 +
pretty(vpa(H(z),3))
 +
</syntaxhighlight>
 +
 +
<syntaxhighlight lang=matlab>
 +
fa = 8000;
 +
fN = fa/2;
 +
wo = 941/fN;  bw = 100/fN;
 +
[b,a] = iirpeak(wo,bw);
 +
fvtool(b,a);
 +
syms z;
 +
N(z) = poly2sym(b,z);
 +
D(z) = poly2sym(a,z);
 +
H(z) = N(z)/D(z);
 +
pretty(vpa(H(z),3))
 +
</syntaxhighlight>
 +
 +
<syntaxhighlight lang=matlab>
 +
fa = 8000; fN = fa/2;
 +
fo = 1000;  bw = 20/fN;
 +
[b,a] = iircomb(fa/fo,bw,'peak');  % ou use a flag 'notch'
 +
fvtool(b,a);
 +
syms z;
 +
N(z) = poly2sym(b,z);
 +
D(z) = poly2sym(a,z);
 +
H(z) = N(z)/D(z);
 +
pretty(vpa(H(z),3))
 +
</syntaxhighlight>
 +
-->
 
{{collapse bottom}}
 
{{collapse bottom}}
  

Edição das 13h29min de 22 de agosto de 2019

Registro on-line das aulas

Unidade 1

Unidade 1

Aula 1 (29 jul)
Aula 2 e 3 (1 e 5 ago)
Aula 4 (8 ago)
  • Revisão de Sinais e Sistemas no tempo discreto em Matlab:
  • Explorar a interface do Matlab.
  • Funções de visualização das variáveis no workspace.
  • Execução de instruções passo a passo.
  • Escrita de script .m
  • Uso da execução das seções de um script.
  • Incremento de valor e execução.
EXEMPLOS:
  • Leia com atenção e execute o exemplo (Moving-Avarage Filter) na página de help da função filter.
  • Revisão de Sinais e Sistemas no tempo discreto em Matlab:
  • Leia com atenção o help Using FFT, abra o script clicando no botão [Open this Example]. Execute o script seção após seção. Note o uso da fft para determinar a frequência das manchas solares.
  • Para melhorar o desempenho no Matlab recomendo que leiam a pagina do Help, . Também gostaria de lembra-los que a tecla F9 executa o código destacado no Help. Programação com scripts .m.
  • Leia sobre manchas solares para entender o que são os dados do segundo exemplo.
Sinais no dominio do tempo e dominio da frequencia. Uso da função fft
Exemplo de uso da FFT 
%% Signal in Time Domain 
% Use Fourier transforms to find the frequency components of a signal buried in noise.
% Specify the parameters of a signal with a sampling frequency of 1 kHz and a signal duration of 1.5 seconds
Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

% Form a signal containing a 50 Hz sinusoid of amplitude 0.7 and a 120 Hz sinusoid of amplitude 1.
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);

% Corrupt the signal with zero-mean white noise with a variance of 4.
X = S + 2*randn(size(t));

% Plot the noisy signal in the time domain. It is difficult to identify the frequency components by looking at the signal X(t).
subplot(211);
plot(1000*t(1:200),X(1:200))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('t (milliseconds)')
ylabel('X(t)')

%% Signal in Frequency Domain
% Compute the Fourier transform of the signal.
Y = fft(X);

% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1 based on P2 and the even-valued signal length L.
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

% Define the frequency domain f and plot the single-sided amplitude spectrum P1. 
% The amplitudes are not exactly at 0.7 and 1, as expected, because of the added noise. 
% On average, longer signals produce better frequency approximations.
f = Fs*(0:(L/2))/L;
subplot(212);
plot(f,P1)
ylim([0 1.05]) 
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

% Now, take the Fourier transform of the original, uncorrupted signal and retrieve the exact amplitudes, 0.7 and 1.0.
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

plot(f,P1) 
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')
  • Amostragem de Sinais (Experimento 1.2)
  • Relembrar teorema da amostragem. Efeito da amostragem abaixo da frequência de Nyquist. Aliasing.
  • Notar que as amostras de um sinal (3 Hz) e um sinal (7 Hz) são idênticas quando amostrado com um sinal de 10 Hz.
Experimento 1.2 
%  Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.2
fs = 10; % frequencia (Hz) de amostragem dos sinais
Ts = 1/fs; fase = 0;
time = 0:Ts:(1-Ts);
f1 = 3; % frequencia (Hz) do sinal s_1
f2 = 7; % frequencia (Hz) do sinal s_2
s_1 = cos(2*pi*f1*time+fase);
s_2 = cos(2*pi*f2*time+fase);
fsa = 1000; % frequência auxiliar de amostragem usada apenas para representação dos sinais originais
Tsa = 1/fsa;
time_aux = 0:Tsa:(1-Tsa);
figure(1);
stem(time,s_1,'ob');
hold on;
plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k');
stem(time,s_2,'+r');
plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m');
hold off;
legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo')
DICAS:
  • No help on-line da Mathworks, usando o botão [Try This Example > Try in your browser], permite executar o código no próprio browser sem ter nenhuma instalação do Matlab. Para verificar que o código realmente é executado mude a amplitude do ruído randômico para 0.1 ou 0.5, insira o comando close all antes da primeira linha, e execute todo o código [Run All]
  • No help do Matlab, usando o botão [Open this Example], é possível executar o código seção a seção.
Aula 5 (12 ago)
  • Revisão de Sinais e Sistemas no tempo discreto em Matlab:
Variação do Experimento 2.2 
%  Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 2.2
% Resposta em frequencia usando a função freqz
N = 1;
num = [1 0 0 0];
den = poly([0.8 0.2])
%den = [1 0.6 -0.16];
% modo 1
%[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]);
%plot(w/pi, abs(H));
% modo 2
%[H,w]=freqz(num,den);
%plot(w/pi, abs(H));
% modo 3
%[H,w]=freqz(num, den, 'whole');
%plot(w/pi, abs(H));
% modo 4
freqz(num, den, 'whole');
figure(2);
zplane(num,den);

%% Resposta em frequencia substituindo z -> e^(jw)
syms z
Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z);
pretty(Hf)
latex(Hf)
N = 1;
w = [0:pi/100:N*pi-pi/100];
plot(w/pi,abs(Hf(exp(1i*w))))
%title(['$' latex(Hf) '$'],'interpreter','latex')
text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex')
xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex')
  1. Verifique a diferença entre os tipos de plots comentados no código.
  2. substitua o denominador de H(z) por dois polos em [-0.8 -0.8].
  3. verifique o que ocorre se forem utilizados polos complexos conjugados [0.3-0.4i 0.3+0.4i 0.1]
  4. verifique o que ocorre se forem utilizados polos complexos não conjugados [0.3-0.4i 0.3+0.8i]
  5. verifique o que ocorre se os polos estiverem fora do circulo unitário [1.2 -0.2]. Interprete este resultado

Aula 1 EAD

Aula 6 (15 ago EAD)
  • Revisão de Sinais e Sistemas no tempo discreto em Matlab:
  • Filtros Digitais
ATIVIDADE 1

Execute no Matlab o código abaixo, e analise os 3 filtros implementados através dos seus zeros e polos. Busque tirar conclusões sobre a influência da posição dos polos e zeros (ver o gráfico do plano z) e correlacione com a resposta de frequência em magnitude (gráfico do freqz). 

%% Experimento 2.3 - Filtros Digitais
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
% FILE: Exp2_3.m
 
%% 1º filtro
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 ]'; P = [p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
 
%% 2º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p1 p1' p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
 
%% 3º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.99*exp(1j*pi/4);
p2 = 0.9*exp(1j*pi/4 - 1j*pi/30);
p3 = 0.9*exp(1j*pi/4 + 1j*pi/30);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p2 p2' p3 p3']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);


ATIVIDADE 2
  • A filtragem de sinais digitais pode ser realizada de diferentes formas:
  • convolução (y = conv(x,h)), onde x(n) é o sinal de entrada e h(n) é a resposta ao impulso do filtro (sistema linear invariante no tempo),
  • filtragem no domínio do tempo (y = a1.x(n)+ a2.x(n-1)+ .. ak.x(n-k));
  • no domínio da frequência (y = ifft(fft(x)fft(h))
Variação do Experimento 3.1 
%% Variação do Experimento 3.1 do livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
% FILE: Ex3_1.m
% Exemplificando as possiveis formas de realizar a filtragem de um sinal x(n)

clc; clear all; close all;
%% Definindo valores iniciais
Nh = 10; Nx = 20;
%Nh = 400; Nx = 10000;
x = ones(1,Nx);
% A resposta ao impulso de um sistema h(n) 
% no filtro FIR aos coeficientes b(n) = h(n) 
h = [1:Nh]; b = h;
%% Filtrando o sinal e medindo tempos

% OPÇÃO 1 - Filtragem utilizando a convolução
% NOTE: length(y) = length(x) + length(h) -1

tic;  % iniciar a contagem do tempo
y1 = conv(x,h); 
t(1) = toc; % terminar a contagem e mostrar tempo no console

% OPÇÃO 2 - filtragem utilizando a equação recursiva
% NOTE: length(y) = length(x)

tic;
y2 = filter(b,1,x);
t(2) = toc;

% OPÇÃO 3 - filtragem utilizando a equação recursiva 
% aumentando o tamanho de x para que length(y3) = length(y1)
x3 = [x zeros(1,length(h)-1)];

tic;
y3 = filter(h,1,x3); 
t(3) = toc;

length_y = length(x) + length(h) - 1;

% OPÇÃO 4 - filtragem utilizando a FFT 
% a y = IFFT(FFT(x)*FFT(h))

tic;
X = fft(x,length_y);
H = fft(h,length_y);
Y4 = X.*H;
y4 = ifft(Y4);
t(4) = toc;

% OPÇÃO 5 - filtragem utilizando a função fftfilt
% a y = IFFT(FFT(x)*FFT(h))

tic
y5 = fftfilt(h,x3);
t(5) = toc;

disp('Comprimento do vetor de saída length(y)')
disp(['    ' num2str([length(y1) length(y2) length(y3) length(y4) length(y5)])])
disp('Tempo usado na filtragem em micro segundos')
disp(['    ' num2str(t*1e6) ' us'])

%%  Plotando o gráfico
subplot(411);stem(y1);
hold on;
stem(y2,'xr');
stem(y3,'+m');
legend('y1', 'y2', 'y3')
hold off
subplot(412);stem(y1, 'ob');legend('y1')
subplot(413);stem(y2, 'xr'); hold on; stem(zeros(size(y1)),'.w');hold off; legend('y2')
subplot(414);stem(y3, '+m');legend('y3')
  • Verificar as funções tic e toc
  • Notar a diferença de tempo de processamento entre os processos de filtragem.
  • A situação pode ser muito diferente conforme muda o tamanho do sinal e ordem do filtro (h(n)). Modifique a resposta ao impulso e o sinal de entrada modificando os valores das variáveis de tamanho: Nh = 10, 100, 1000; Nx = 20, 1000, 10000;
  • Em função do sistema operacional e reserva de memória para as variáveis é importante desprezar a primeira medida de tempo. Realize 3 medidas de tempo para cada uma das 5 opções de filtragem, com pelo menos duas combinações de comprimento Nh e Nx. Relate os resultados obtidos no comentário da atividade no Moodle.
Aula 7 (19 ago)
  • Exercício - Sinal DTMF com ruído
  • Verifique se o Matlab está reproduzindo corretamente o som.
%% Carregando o som
clear, close, clc
load handel;

%% Reproduzindo o som 
sound(y,Fs)
 
% Reproduzindo o som 
%soundsc(y,Fs)
 
% Reproduzindo o som 
%player = audioplayer(y, Fs);
%play(player);
  • Usando o Matlab (ou Audacity) para gerar um sinal DTMF correspondente a um número N e adicionar um ruido ao sinal. Opcionalmente utilize um sinal DTMF gravado
  • Utilizar uma frequência de amostragem de 8000Hz de fazer a duração do sinal igual a 2 segundos.
Sinal 1234567890*#
  • Para adicionar o ruído utilize a função y = awgn(x,snr), ou y = x + nivel*randn(n).
  • Observe este sinal no domínio do tempo (DT) e domínio da frequência (DF).
%% Carregando o som
clear, close, clc
[y,Fs] = audioread('DTMF_8kHz.ogg');

%% Reproduzindo o som 
sound(y,Fs)

%% Visualizando o som no DT
time = [0:length(y)-1]'/Fs;
plot(time',y'); xlabel('segundos');
xlim([0 time(end)]), ylim([-1 1]);

%% Visualizando o som no DF
Nfreq = length(y);
freq = linspace(0,2*pi,Nfreq)'*Fs/pi/2;
Y = fft(y,Nfreq)/Nfreq;
plot(freq,abs(Y)); xlabel('Hertz');
xlim([0 Fs/2]);
  • Utilizar no Audacity um sinal DTMF ("1234567890") com fa= 8kHz
  • Visualizar no domínio do tempo e frequência.
  • Realizar a filtragem passa-baixas com fc = 1066 Hz, (selecionar a maior atenuação permitida)
  • Realizar a filtragem passa-faixa com f0 = 770 Hz e B = 70Hz (selecionar a maior ordem permitida)
  • Repetir o procedimento anterior para um sinal de ruído branco.
  • Consulte a documentação do Matlab sobre 
     fft, ifft, fftshift, randn
  • Consulte a documentação do Matlab sobre 
     plot, grid, subplot, hold, xlabel, ylabel, title, legend, xlim, ylim, log10, log
  • Consulte a documentação do Matlab sobre text, zp2tf, tf2zp, fftfilt, awgn
  • Ver pag. 141 a 145 e 230 a 235 de [1]

Unidade 2

Unidade 2
Aula 8 (22 ago)
  • Filtros Analógicos:
  • Função de transferência
  • Resposta em frequência: para obter a resposta em frequência é necessário avaliar
  • O projeto de filtros analógicos é realizado em 2 etapas:
  1. projeto de um filtro passa baixas (LP) protótipo normalizado com frequência de passagem
  2. transformação em frequência para o tipo de filtro (LP, HP, BP ou BS)
  • Análise básica de filtros analógicos com Matlab.
Dado um sistema linear invariante no tempo, representado pela função de transferência , obter a resposta de frequência do sistema (Magnitude e Fase). 
b = [1 1];
a = [1 1 5];
[z1,p1,k]=tf2zp(b,a)
z2 = roots(b);
p2 = roots(a);
zplane(b,a);
%%
freqs(b,a);
%%
syms s  w
H(s) = (s+1)/(s^2 + s + 5);
pretty(H(1j*w))
latex(H(1j*w))
%%
ws = logspace(-2, 1, 1000);
h = H(1j*ws);
subplot(211)
semilogx(ws,abs(h)); grid on;
subplot(212)
semilogx(ws,angle(h)/pi*180); grid on;
  • Projeto de filtros analógicos do tipo Butterworth
  • A aproximação de magnitude de filtros analógicos pode ser realizado usando as aproximações de Butterworth, Chebyshev (tipo 1 ou 2) e Cauer.

TiposFiltrosHs.png

Proposta de exercício
  • Use os polinômios de Butterworth com ordens de 1 a 10 mostrados na tabela abaixo para obter os filtros .
n Fatores Polinomiais de
1
2
3
4
5
6
7
8
9
10
  • Escolha uma ordem n (entre 5 e 10)
  • Plote a resposta em frequência em escala log da amplitude (em dB) e da fase (em rad/pi).
  • Qual é o ganho do filtro na banda passante?
  • Qual é a frequência de corte (-3dB) do filtro.
  • Qual é o salto de de fase que ocorre em algumas frequências?
  • Qual é o fator de atenuação em dB/decada após a frequência de corte?
  • Faça o diagrama de polos e zeros desse filtro.
  • Procure observar o que ocorre com a posição dos polos do filtro.
  • Calcule o valor do módulo dos pólos.


Avaliações

  • Entrega dos diversas Atividades Extraclasse ao longo do semestre.
  • Provas escritas A1 e A2
  • Entrega do Projeto Final. O projeto é avaliado nos quesitos:
1) Implementação do Sistema,
2) Documentação,
3) Avaliação Global do aluno no projeto.
  • Entrega dos Atividades Extraclasse ao longo do semestre AE1 a AE(N). A entrega, detalhes e prazos de cada AE serão indicados na plataforma Moodle
  1. ↑ 1,0 1,1 1,2 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
Disponível em “https://wiki.sj.ifsc.edu.br/index.php?title=PSD29007-Engtelecom(2019-2)_-_Prof._Marcos_Moecke&oldid=160594”