CIL29003-2015-2: mudanças entre as edições
| Linha 87: | Linha 87: | ||
{{Collapse top |Aula 1 - 5/10/15: Apresentação da disciplina}} | {{Collapse top |Aula 1 - 5/10/15: Apresentação da disciplina}} | ||
Seção 2.2 e 2.3 do Pedroni. | |||
* Apresentação da disciplina, plano de aula, trabalhos e métodos de avaliação. | * Apresentação da disciplina, plano de aula, trabalhos e métodos de avaliação. | ||
| Linha 107: | Linha 109: | ||
##Circuitos combinacionais versus sequenciais. | ##Circuitos combinacionais versus sequenciais. | ||
##Circuitos integrados, placas de circuitos e tensões. | ##Circuitos integrados, placas de circuitos e tensões. | ||
{{Collapse bottom}} | |||
{{Collapse top |Aula 2 - 6/10/15: Representações Binárias}} | |||
==Sistemas de numeração== | |||
Observe a Figura do odômetro. | |||
[[Arquivo:odometro.jpg|100px]] | |||
Suponha que o mesmo possua somente duas roldanas de algarismos e que cada algarismo represente exatamente 1 km. Qual a quantidade máxima de quilômetros que o suposto odômetro pode representar? | |||
{| style="border-style: solid; border-width: 20px" | |||
|- | |||
| 0 || 0 | |||
|- | |||
| 0 || 1 | |||
|- | |||
| 0 || ... | |||
|- | |||
| 0 || 8 | |||
|- | |||
| 0 || 9 | |||
|- | |||
| 1 || 0 | |||
|- | |||
| 1 || 1 | |||
|- | |||
| 1 || ... | |||
|- | |||
| 1 || 8 | |||
|- | |||
| 1 || 9 | |||
|- | |||
| ... || ... | |||
|- | |||
| 9 || 0 | |||
|- | |||
| 9 || 1 | |||
|- | |||
| 9 || ... | |||
|- | |||
| 9 || 8 | |||
|- | |||
| 9 || 9 | |||
|- | |||
| 0 || 0 | |||
|- | |||
| ... || ... | |||
|} | |||
Agora suponha que cada roldana tenha impresso somente os valores '''0''' e '''1'''. Qual a quantidade máxima de quilômetros que o mesmo pode representar? | |||
{| style="border-style: solid; border-width: 20px" | |||
|- | |||
| MSB || LSB | |||
|- | |||
| 0 || 0 | |||
|- | |||
| 0 || 1 | |||
|- | |||
| 1 || 0 | |||
|- | |||
| 1 || 1 | |||
|- | |||
| 0 || 0 | |||
|- | |||
| ... || ... | |||
|} | |||
Obs.: LSB (''least significant bit'') é o bit menos significativo que é o equivalente as unidades na representação decimal. MSB (''most significant bit'') é o bit mais significativo e sempre ocupa a posição mais a esquerda da representação. | |||
Este sistema de numeração é conhecido como binário ("que tem aspecto dual, ou é formado por dois elementos ou partes"). | |||
No caso anterior como poderíamos representar maiores quantidades de quilômetros? | |||
Em outra linha de raciocínio, como pode-se aumentar a capacidade de contagem quilométrica, mais do que o permitido no sistema decimal? Aumenta-se o número de símbolos disponíveis em cada roldana. Por exemplo, se adotarmos a seguinte simbologia: 0, 1, ..., 8, 9, A, B, C, D, E, F, pode-se ter a seguinte representação quilométrica: | |||
{| style="border-style: solid; border-width: 20px" | |||
|- | |||
| 0 || 0 | |||
|- | |||
| 0 || 1 | |||
|- | |||
| 0 || ... | |||
|- | |||
| 0 || E | |||
|- | |||
| 0 || F | |||
|- | |||
| 1 || 0 | |||
|- | |||
| 1 || 1 | |||
|- | |||
| 1 || ... | |||
|- | |||
| 1 || E | |||
|- | |||
| 1 || F | |||
|- | |||
| ... || ... | |||
|- | |||
| 9 || 0 | |||
|- | |||
| 9 || 1 | |||
|- | |||
| 9 || ... | |||
|- | |||
| 9 || E | |||
|- | |||
| 9 || F | |||
|- | |||
| A || 0 | |||
|- | |||
| A || 1 | |||
|- | |||
| ... || ... | |||
|- | |||
| F || E | |||
|- | |||
| F || F | |||
|- | |||
| 0 || 0 | |||
|- | |||
| ... || ... | |||
|} | |||
Este é o sistema de numeração hexadecimal. | |||
Um outro importante sistema de numeração é o octal. | |||
Perceba que é possível a construção de qualquer sistema de numeração. | |||
==Conversão entre sistemas de numeração== | |||
Como é de conhecimento geral, o sistema de numeração mais utilizado port seres humanos é o sistema decimal. Não tão conhecido assim, mas muito utilizado, é o sistema de numeração binário, amplamente adotado nos sistema informatizados. | |||
Uma pergunta que cabe é, por exemplo, quando digitamos algum número em uma calculadora, o que acontece? Em primeiro lugar, a calculadora apresenta o valor digitado no visor, para termos certeza do que digitamos e, em seguida, internamente à calculadora este valor é convertido para binário, o sistema de numeração que ela entende. Como esta conversão ocorre? | |||
===Conversão de outras bases para a base decimal=== | |||
A regra geral para conversão de binário para um número decimal é assim expressa: | |||
<math>y = \sum_{k=0}^{N-1} a_{N-1-k} 2^{N-1-k}</math> | |||
onde <math>y</math> é um número decimal e <math>a = a_{N-1} \dots a_1a_0</math> é sua representação binária usual. | |||
Observe que esta regra pode ser estendida para qualquer sistema de numeração. | |||
Por exemplo, vamos converter <math>11001_2</math> para a base decimal. | |||
<math>11001_2 = 1\cdot2^4+1\cdot2^3+0\cdot2^2+0\cdot2^1+1\cdot2^0 = 1\cdot16+1\cdot8+0\cdot4+0\cdot2+1\cdot1 = 25</math> | |||
Outro exemplo, vamos converter <math>703_8</math> para a base decimal. | |||
<math>703_8 = 7\cdot8^2+0\cdot8^1+3\cdot8^0 = 7\cdot64+0\cdot8+3\cdot1 = 451</math> | |||
===Conversão da base decimal para outras bases=== | |||
A conversão de um número da base decimal para qualquer outra base pode ser efetivada usando-se divisões sucessivas do valor decimal pela base a ser convertido, tomando-se com resultado os sucessivos restos dessa divisão. | |||
Por exemplo, para converter 23 para a base binária devemos fazer o seguinte procedimento: | |||
[[Arquivo:ConversaoDecimalBinario.jpg|300px]] | |||
O procedimento para outras bases é o mesmo, por exemplo, para converter-se 258 para a base '''8''', utiliza-se o mesmo procedimento acima, substituindo os valores 2 por 8, no divisor. | |||
===Conversão entre bases de origem binária=== | |||
Para conversão entre as bases binária, octal e hexadecimal, basta fazer-se o uso das seguintes tabelas de conversão. | |||
{| style=1 | |||
|- | |||
| octal || binário | |||
|- | |||
| 0 || 000 | |||
|- | |||
| 1 || 001 | |||
|- | |||
| 2 || 010 | |||
|- | |||
| 3 || 011 | |||
|- | |||
| 4 || 100 | |||
|- | |||
| 5 || 101 | |||
|- | |||
| 6 || 110 | |||
|- | |||
| 7 || 111 | |||
|} | |||
{| style=1 | |||
|- | |||
| hexadecimal || binário | |||
|- | |||
| 0 || 0000 | |||
|- | |||
| 1 || 0001 | |||
|- | |||
| 2 || 0010 | |||
|- | |||
| 3 || 0011 | |||
|- | |||
| 4 || 0100 | |||
|- | |||
| 5 || 0101 | |||
|- | |||
| 6 || 0110 | |||
|- | |||
| 7 || 0111 | |||
|- | |||
| 8 || 1000 | |||
|- | |||
| 9 || 1001 | |||
|- | |||
| A || 1010 | |||
|- | |||
| B || 1011 | |||
|- | |||
| C || 1100 | |||
|- | |||
| D || 1101 | |||
|- | |||
| E || 1110 | |||
|- | |||
| F || 1111 | |||
|} | |||
Por exemplo, para converter <math>730_8</math> para binário, deve-se tomar dígito a dígito da tabela acima e ir montando o valor binário equivalente: <math>7_8 = 111_2</math>, <math>3_8 = 011_2</math> e <math>0_8 = 000_2</math>. Portanto o resultado da conversão é <math> 111011000_2</math> | |||
Se desejarmos converter da base octal para a hexadecimal e vice-versa, a maneira mais fácil é primeiro a conversão da base de origem para a base binária e, em seguida, desta para a base destino. Por exemplo, para converter <math> FACA_{16}</math> para a base octal procedemos primeiro a conversão para a base binária (<math> 1111101011001010_2</math>) e em seguida, tomando três a três dígitos a partir do LSB, convertemos para o octal usando a tabela, resultando em <math> 175312_8</math> | |||
{{Collapse bottom}} | |||
{{Collapse top |Aula 3 - 12/10/15: Representações binárias}} | |||
Seção 2.3 a 2.7 do Pedroni | |||
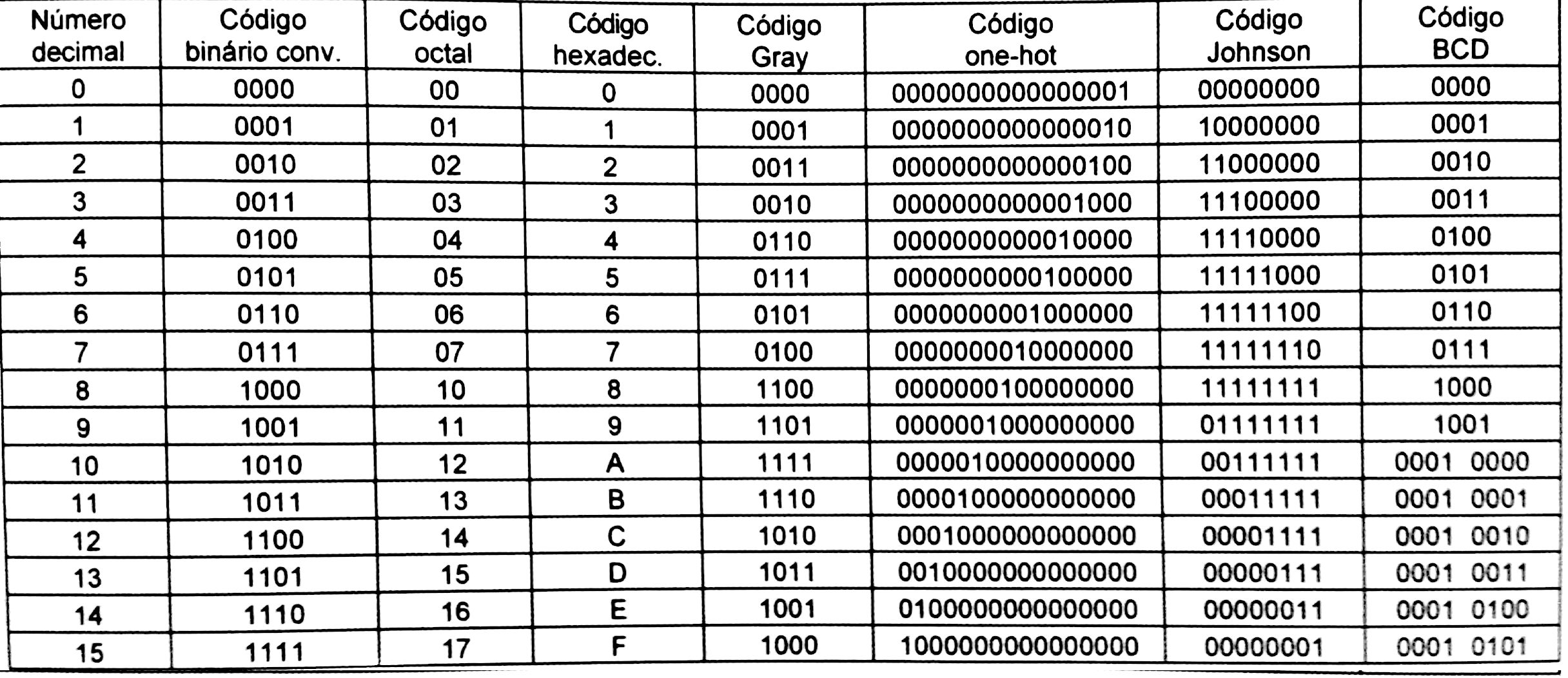
A tabela a seguir representa os númerios decimais de 0 a 15 pelos códigos binário convencinal, octal, hexadecimal, Gray, one-hot, Johnson e BCD. | |||
[[Arquivo:representacoes_binarios.jpg |Tabela de equivalência entre códigos|800px]] | |||
Código Gray: código de distância unitária porque a distância entre duas palavras adjacentes é sempre 1 bit [http://pt.wikipedia.org/wiki/C%C3%B3digo_de_Gray]. | |||
Código one-hot: frequentemente utilizado na codificação de máquinas de estados [http://en.wikipedia.org/wiki/One-hot] [http://en.wikipedia.org/wiki/Ring_counter]. | |||
Código Johnson: Também utilizado para representar máquinas de estados. É um código intermediário entre o one-hot e o Gray, em termos de uso do hardware. | |||
Código BCD (''binary-coded decimal''): cada dígito de um número decimal é representado por um conjunto de 4 bits do código binário. | |||
==Códigos para números negativos== | |||
Como representar sinal no código binário? | |||
===Código sinal-magnitude=== | |||
Nesse caso o MSB representa o sinal: 0 = + e 1 = -. Assim sendo, o MSB não faz parte da representação sequencial binária do número. Ex: | |||
#0000 = +0 | |||
#1001 = -1 | |||
#110011 = -19 | |||
#010011 = +19 | |||
#111100111 = -231 | |||
===Código complemento de um=== | |||
Se o MSB for 0 (número positivo), para obter o equivalente negativo, basta inverter todos os bits. Ex: | |||
#0000 = +0 ==> 1111 = -0 | |||
#0101 = +5 ==> 1010 = -5 | |||
===Código complemento de dois=== | |||
Esta é a opção adota para representar números negativos em praticamento todos os computadores e outros sistema digitais. | |||
A representação binária de um número negativo é obtida tomando sua representação positiva, invertendo todos os bits e então adicionando um a ele. Exemplo, -7 (5 bits) é igual a 00111 ==> 11000 + 1 ==> 11001 | |||
Regra prática | |||
Para cálculo do equivalente decimal de um número representado em complemento de dois, pode-se fazer uso do modelo apresentado no exemplo: | |||
{| border=1 | |||
|- | |||
| 1 || 0 || 1 || 1 || 0 || 1 | |||
|- | |||
| -32 || + 0 || +8 || +4 || +0 || +1 | |||
|} | |||
Ao somar-se todos os valores da segunda linha da tabela acima, obtém-se o valor 19. | |||
Usando números de 8 bits, Calcule o complemento de dois para: | |||
#-0 | |||
#-1 | |||
#-17 | |||
#-123 | |||
#-128 | |||
Algum problema? | |||
{{Collapse bottom}} | {{Collapse bottom}} | ||
Edição das 13h54min de 1 de outubro de 2015
1 Dados Importantes
Professor: Odilson Tadeu Valle
Email: odilson@ifsc.edu.br
Atendimento paralelo: ?ª das?? às ?? e ?ª das ?? às ??. Local: Lab. de Desenvolvimento.
- Avaliações
- 3 avaliações (P1, P2 e P3) mais um projeto final (PF).
- Cada uma das avaliações terá terá um conceito numérico: A, B, C e D. Conceito mínimo para não necessitar reavaliação: C.
- Um ou mais conceitos D implica na realização da reavaliação: uma única a ser realizada no último dia de aula.
IMPORTANTE: o direito de recuperar uma avaliação em que se faltou somente existe mediante justificativa reconhecida pela coordenação. Assim, deve-se protocolar a justificativa no prazo de 48 horas, contando da data e horário da avaliação e aguardar o parecer da coordenação.
1.1 Plano de Ensino
Cronograma_de_atividades_(CIL-EngTel)
1.2 IFSC-Cloud
O IFSC-Cloud permite que qualquer usuário cadastrado acesse vários programas oficiais do ISFC remotamente, entre outros o Quartus que será utilizado intensivamente nesta disciplina. Inclusive permite que o aluno deixe processos/simulações longas rodando e verificar os resultados em um próximo acesso.
Para os alunos ainda não cadastrados na IFSC-Cloud, peça para o professor fazer seu cadastro. Após o cadastro siga exatamente TODOS os passos de Acesso_ao_IFSC-CLOUD. Caso tenha algum problema com a senha, entre em contato com o professor
1.3 Listas de exercícios
| Lista para a primeira avaliação |
|---|
|
| Lista para a segunda avaliação |
|---|
|
| Lista para a terceira avaliação |
|---|
|
2 Diário de aulas
| Aula 1 - 5/10/15: Apresentação da disciplina |
|---|
|
Seção 2.2 e 2.3 do Pedroni.
|
| Aula 2 - 6/10/15: Representações Binárias | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
2.1 Sistemas de numeraçãoObserve a Figura do odômetro. Suponha que o mesmo possua somente duas roldanas de algarismos e que cada algarismo represente exatamente 1 km. Qual a quantidade máxima de quilômetros que o suposto odômetro pode representar?
Agora suponha que cada roldana tenha impresso somente os valores 0 e 1. Qual a quantidade máxima de quilômetros que o mesmo pode representar?
Obs.: LSB (least significant bit) é o bit menos significativo que é o equivalente as unidades na representação decimal. MSB (most significant bit) é o bit mais significativo e sempre ocupa a posição mais a esquerda da representação. Este sistema de numeração é conhecido como binário ("que tem aspecto dual, ou é formado por dois elementos ou partes"). No caso anterior como poderíamos representar maiores quantidades de quilômetros? Em outra linha de raciocínio, como pode-se aumentar a capacidade de contagem quilométrica, mais do que o permitido no sistema decimal? Aumenta-se o número de símbolos disponíveis em cada roldana. Por exemplo, se adotarmos a seguinte simbologia: 0, 1, ..., 8, 9, A, B, C, D, E, F, pode-se ter a seguinte representação quilométrica:
Este é o sistema de numeração hexadecimal. Um outro importante sistema de numeração é o octal. Perceba que é possível a construção de qualquer sistema de numeração. 2.2 Conversão entre sistemas de numeraçãoComo é de conhecimento geral, o sistema de numeração mais utilizado port seres humanos é o sistema decimal. Não tão conhecido assim, mas muito utilizado, é o sistema de numeração binário, amplamente adotado nos sistema informatizados. Uma pergunta que cabe é, por exemplo, quando digitamos algum número em uma calculadora, o que acontece? Em primeiro lugar, a calculadora apresenta o valor digitado no visor, para termos certeza do que digitamos e, em seguida, internamente à calculadora este valor é convertido para binário, o sistema de numeração que ela entende. Como esta conversão ocorre? 2.2.1 Conversão de outras bases para a base decimalA regra geral para conversão de binário para um número decimal é assim expressa:
onde é um número decimal e é sua representação binária usual. Observe que esta regra pode ser estendida para qualquer sistema de numeração. Por exemplo, vamos converter para a base decimal.
Outro exemplo, vamos converter para a base decimal.
2.2.2 Conversão da base decimal para outras basesA conversão de um número da base decimal para qualquer outra base pode ser efetivada usando-se divisões sucessivas do valor decimal pela base a ser convertido, tomando-se com resultado os sucessivos restos dessa divisão. Por exemplo, para converter 23 para a base binária devemos fazer o seguinte procedimento: O procedimento para outras bases é o mesmo, por exemplo, para converter-se 258 para a base 8, utiliza-se o mesmo procedimento acima, substituindo os valores 2 por 8, no divisor. 2.2.3 Conversão entre bases de origem bináriaPara conversão entre as bases binária, octal e hexadecimal, basta fazer-se o uso das seguintes tabelas de conversão.
Por exemplo, para converter para binário, deve-se tomar dígito a dígito da tabela acima e ir montando o valor binário equivalente: , e . Portanto o resultado da conversão é Se desejarmos converter da base octal para a hexadecimal e vice-versa, a maneira mais fácil é primeiro a conversão da base de origem para a base binária e, em seguida, desta para a base destino. Por exemplo, para converter para a base octal procedemos primeiro a conversão para a base binária () e em seguida, tomando três a três dígitos a partir do LSB, convertemos para o octal usando a tabela, resultando em |
| Aula 3 - 12/10/15: Representações binárias | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Seção 2.3 a 2.7 do Pedroni A tabela a seguir representa os númerios decimais de 0 a 15 pelos códigos binário convencinal, octal, hexadecimal, Gray, one-hot, Johnson e BCD.
Código Gray: código de distância unitária porque a distância entre duas palavras adjacentes é sempre 1 bit [1]. Código one-hot: frequentemente utilizado na codificação de máquinas de estados [2] [3]. Código Johnson: Também utilizado para representar máquinas de estados. É um código intermediário entre o one-hot e o Gray, em termos de uso do hardware. Código BCD (binary-coded decimal): cada dígito de um número decimal é representado por um conjunto de 4 bits do código binário. 2.3 Códigos para números negativosComo representar sinal no código binário? 2.3.1 Código sinal-magnitudeNesse caso o MSB representa o sinal: 0 = + e 1 = -. Assim sendo, o MSB não faz parte da representação sequencial binária do número. Ex:
2.3.2 Código complemento de umSe o MSB for 0 (número positivo), para obter o equivalente negativo, basta inverter todos os bits. Ex:
2.3.3 Código complemento de doisEsta é a opção adota para representar números negativos em praticamento todos os computadores e outros sistema digitais. A representação binária de um número negativo é obtida tomando sua representação positiva, invertendo todos os bits e então adicionando um a ele. Exemplo, -7 (5 bits) é igual a 00111 ==> 11000 + 1 ==> 11001 Regra prática Para cálculo do equivalente decimal de um número representado em complemento de dois, pode-se fazer uso do modelo apresentado no exemplo:
Ao somar-se todos os valores da segunda linha da tabela acima, obtém-se o valor 19. Usando números de 8 bits, Calcule o complemento de dois para:
Algum problema? |