CEL18702 AULA10: mudanças entre as edições
Ir para navegação
Ir para pesquisar
| (19 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
=Lista de Exercício 3= | =Lista de Exercício 3= | ||
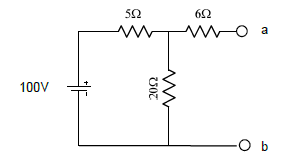
1. Diga qual o valor da resistência que solicita uma corrente de 5A quando ligada aos pontos a e b do circuito abaixo: | |||
[[Imagem: | [[Imagem:fig42_CEL18702.png|center]] | ||
{{collapse top|Solução}} | |||
<math>R=6\Omega\,</math> | |||
{{collapse bottom}} | |||
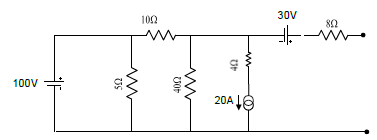
2. Encontre o equivalente de Norton para o circuito abaixo: | |||
[[Imagem:fig43_CEL18702.png|center]] | |||
{{collapse top|Solução}} | {{collapse top|Solução}} | ||
<math> | <math>R_{Th}=16\Omega\,,V_{Th}=-50V</math> | ||
{{collapse bottom}} | |||
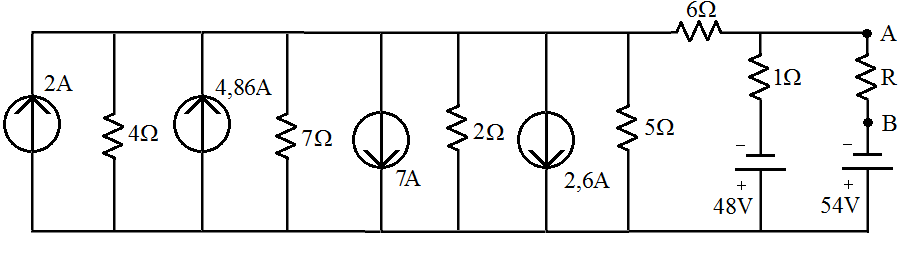
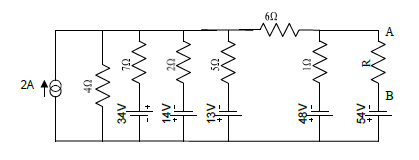
3. Determine R para que a corrente que que passe pelos pontas A e B seja de 2A: | |||
[[Imagem:fig44_CEL18702.png|center]] | |||
{{collapse top|Solução}} | |||
3.1 Substituindo as três primeiras fontes de tensão por fonte de corrente: | |||
[[Imagem:fig46_CEL18702.png|center|500px]] | |||
3.2 Fazendo a substituição das quatro fontes de corrente em paralelo (teorema de Millman): | |||
<math>I_{eq}=2+4,86-7-2,6=-2,74A\,</math> | |||
3.3 Fazendo a substituição da resistência equivalente desse paralelo: | |||
<math>R_{ | <math>\frac{1}{R_{eq}}=\frac{1}{4}+\frac{1}{7}+\frac{1}{2}+\frac{1}{5}=0,92\Omega\,</math> | ||
3.4 Substituindo a fonte de corrente equivalente por fonte de tensão, juntamente com a resistência equivalente: | |||
<math>V_{eq}=I_{eq}.R_{eq}=-2,74*0,92=-2,52V\,</math> | |||
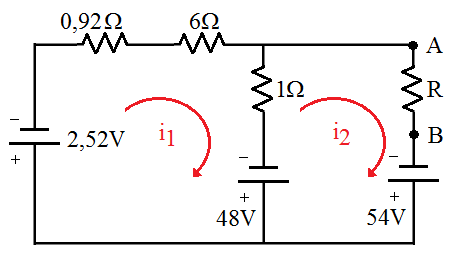
[[Imagem:fig46b_CEL18702.png|center|300px]] | |||
<math> | 3.5 Sabendo-se que a corrente <math>I_2=2A</math> tem-se: | ||
'''Malha 1''' | |||
<math> | <math>2,52+0,92i_1+6i_1+1(i_1-i_2)-48=0\,</math> | ||
<math>2,52+0,92i_1+6i_1+1i_1-2-48=0\,</math> | |||
<math> | <math>7,92i_1=48-2,52+2\,</math> | ||
<math>i_1=\frac{47,44}{7,92}=6 A\,</math> | |||
'''Malha 2''' | |||
<math>R.i_2-54+48+1(i_2-i_1)=0\,</math> | |||
<math>2R-54+48+1(2-6)=0\,</math> | |||
<math>R=\frac{54-48+4}{2}=5\Omega\,</math> | |||
;Resultado: | ;Resultado: | ||
<math>R=5\Omega\,</math> | |||
<math> | |||
{{collapse bottom}} | {{collapse bottom}} | ||
| Linha 88: | Linha 84: | ||
[1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf | [1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf | ||
[2] http://www.ufrgs.br/eng04030/Aulas/teoria/cap_04/assocfon.htm | |||
----- | ----- | ||
{| border="1" cellpadding="5" cellspacing="0" | {| border="1" cellpadding="5" cellspacing="0" | ||
! style="background: #ffd700;" | [[ | ! style="background: #ffd700;" | [[CEL18702_AULA09 | << ]] | ||
! style="background: #faebd7;" | [[CEL18702 | <> ]] | ! style="background: #faebd7;" | [[CEL18702 | <> ]] | ||
! style="background: #ffd700;" | [[ | ! style="background: #ffd700;" | [[CEL18702_AULA11 | >> ]] | ||
|} | |} | ||
Edição atual tal como às 16h53min de 7 de março de 2016
1 Lista de Exercício 3
1. Diga qual o valor da resistência que solicita uma corrente de 5A quando ligada aos pontos a e b do circuito abaixo:
| Solução |
|---|
|
|
2. Encontre o equivalente de Norton para o circuito abaixo:
| Solução |
|---|
|
|
3. Determine R para que a corrente que que passe pelos pontas A e B seja de 2A:
2 Referências
[1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf
[2] http://www.ufrgs.br/eng04030/Aulas/teoria/cap_04/assocfon.htm
| << | <> | >> |
|---|