PSD29007-Engtelecom(2017-1) - Prof. Marcos Moecke

Registro on-line das aulas

Unidade 1

Aula 1 (10 Fev)

• Apresentação da disciplina

• Revisão de Sinais e Sistemas no tempo discreto em Matlab:

• Resposta de sistemas LTI (Experimento 1.1)

• Relembrar o conceito de equação de diferenças de um sistema LTI discreto e resposta ao impulso.
• Resposta ao delta de Kronecker do sistema LTI discreto

$a_{0}y[n]+a_{1}y[n-1]+a_{2}y[n-2]+...+a_{N}y[n-N]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]+...+b_{M}x[n-M]$

onde $a_{0}=1$, $a_{1}=-1/\alpha$ e $b_{1}=1$ logo $y[n]=1/\alpha .y[n-1]+x[n]$

%  Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.1
alpha = 1.15; N = 256;
x = [1 zeros(1,N)];
y = filter(1,[1 -1/alpha],x);
stem(y);

• Amostragem de Sinais (Experimento 1.2)

• Relembrar teorema da amostragem. Efeito da amostragem abaixo da frequência de Nyquist. Aliasing.
• Notar que as amostras de um sinal $s_{1}(t)=cos(2\pi \times 3t)$ (3 Hz) e um sinal $s_{2}(t)=cos(2\pi \times 7t)$ (7 Hz) são idênticas quando amostrado com um sinal de 10 Hz.

%  Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.2
fs = 10; % frequencia (Hz) de amostragem dos sinais
Ts = 1/fs; fase = 0;
time = 0:Ts:(1-Ts);
f1 = 3; % frequencia (Hz) do sinal s_1
f2 = 7; % frequencia (Hz) do sinal s_2
s_1 = cos(2*pi*f1*time+fase);
s_2 = cos(2*pi*f2*time+fase);
fsa = 1000; % frequência auxiliar de amostragem usada apenas para representação dos sinais originais
Tsa = 1/fsa;
time_aux = 0:Tsa:(1-Tsa);
figure(1);
stem(time,s_1,'ob');
hold on;
plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k');
stem(time,s_2,'+r');
plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m');
hold off;
legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo')

• Uso do Matlab: Help, F9 executa o código destacado no Help. Programação com scripts .m, Execução de seções e variação de valores nos scripts,
• Ver no Matlab: zeros, ones, plot, stem, subplot, filter.
• Uso de gráficos no Matlab.

• Ver pag. 65 a 71 de
• Ver também PDF Documentation for MATLAB. Principalmente MATLAB Primer.

Aula 2 (13 Fev)

• Revisão de Sinais e Sistemas no tempo discreto em Matlab:

• Filtragem de Sinais (Experimentos 1.3, 2.1 e 2.2)
• Consulte a documentação do Matlab sobre

   roots, poly, linspace, logspace
  

• Uso de residue, residuez, pretty, latex, freqs, freqz, syms, symfun, zplane.
• Ver também o Publish para a geração automática de relatórios em html, doc, pdf, latex ou ppt. Ver também Publishing MATLAB Code.
• Ver pag. 138 a 141 de

Variação do Experimento 2.2

% Exemplos e Experimentos baseados no livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. %% Experimento 2.2 % Resposta em frequencia usando a função freqz N = 1; num = [1 0 0 0]; den = poly([0.8 0.2]) %den = [1 0.6 -0.16]; % modo 1 %[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]); %plot(w/pi, abs(H)); % modo 2 %[H,w]=freqz(num,den); %plot(w/pi, abs(H)); % modo 3 %[H,w]=freqz(num, den, 'whole'); %plot(w/pi, abs(H)); % modo 4 freqz(num, den, 'whole'); figure(2); zplane(num,den); %% Resposta em frequencia substituindo z -> e^(jw) syms z Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z); pretty(Hf) latex(Hf) N = 1; w = [0:pi/100:N*pi-pi/100]; plot(w/pi,abs(Hf(exp(1i*w)))) %title(['$' latex(Hf) '$'],'interpreter','latex') text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex') xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex') Verifique a diferença entre os tipos de plots comentados no código. substitua o denominador de H(z) por dois polos em [-0.8 -0.8]. verifique o que ocorre se forem utilizados polos complexos conjugados [0.3-0.4i 0.3+0.4i 0.1] verifique o que ocorre se forem utilizados polos complexos não conjugados [0.3-0.4i 0.3+0.8i] verifique o que ocorre se os polos estiverem fora do circulo unitário [1.2 -0.2]. Interprete este resultado

Aula 3 (17 Fev)

• Revisão de Sinais e Sistemas no tempo discreto em Matlab:

• Filtragem de Sinais

Variação do Experimento 3.1

%% Variação do Experimento 3.1 do livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. % FILE: Ex3_1.m % Exemplificando as possiveis formas de realizar a filtragem de um sinal x(n) clc; clear all; close all; %% Definindo valores iniciais Nh = 10; Nx = 20; %Nh = 400; Nx = 10000; x = ones(1,Nx); % A resposta ao inpulso de um sistema h(n) % no filtro FIR aos coeficientes b(n) = h(n) h = [1:Nh]; b = h; %% Filtrando o sinal e medindo tempos % Filtragem utilizando a convolução % NOTE: length(y) = length(x) + length(h) -1 tic; % iniciar a contagem do tempo y1 = conv(x,h); t(1) = toc; % terminar acontagem e mostrar tempo no console % filtragem utilizando a equação recursiva % NOTE: length(y) = length(x) tic; y2 = filter(b,1,x); t(2) = toc; % filtragem utilizando a equação recursiva % aumentando o tamanho de x para que length(y3) = length(y1) x3 = [x zeros(1,length(h)-1)]; tic; y3 = filter(h,1,x3); t(3) = toc; length_y = length(x) + length(h) - 1; % filtragem utilizando a FFT % a y = IFFT(FFT(x)*FFT(h)) tic; X = fft(x,length_y); H = fft(h,length_y); Y4 = X.*H; y4 = ifft(Y4); t(4) = toc; % filtragem utilizando a função fftfilt % a y = IFFT(FFT(x)*FFT(h)) tic y5 = fftfilt(h,x3); t(5) = toc; disp('Comprimento do vetor de saída length(y)') disp([' ' num2str([length(y1) length(y2) length(y3) length(y4) length(y5)])]) disp('Tempo usado na filtragem em micro segundos') disp([' ' num2str(t*1e6) ' us']) %% Plotando o gráfico subplot(411);stem(y1); hold on; stem(y2,'xr'); stem(y3,'+m'); legend('y1', 'y2', 'y3') hold off subplot(412);stem(y1, 'ob');legend('y1') subplot(413);stem(y2, 'xr'); hold on; stem(zeros(size(y1)),'.w');hold off; legend('y2') subplot(414);stem(y3, '+m');legend('y3')

• Análise de Sinais (Experimento 3.2) - Análise de um sistema h[n] correspondente a um filtro passa-faixa, utilizando um sinal de entrada x[n] senoidal (ou um sinal r[n] de ruído branco). Análise da entrada x[n] e saída y[n] usando a fft.

Variação do Experimento 3.2

%% Variação do Experimento 3.2 do livro: % DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235. % FILE: Ex3_2.m % Análise de sinais no domínio da frequência fs = 200; % frequência de amostragem f_sinal = 10; A_sinal = 1; % freqüência e amplitude do sinal T = 1; % Duração do sinal k_noise = 0.2; % Intensidade do ruído snr = 0; time = 0 : 1/fs : (T-1/fs); L = length(time); freq = time * fs/T; % Sinal x(n) com amplitude A_sinal e frequencia de f_sinal (Hz) x = A_sinal*sin(2*pi*f_sinal.*time); % Adicionando um ruido com a função randn noise = k_noise*randn(1,fs*T); x1 = x + noise; % Adicionando um ruido com a função awgn x2 = awgn(x,snr); % Obtendo o sinal no domínio da frequencia X = abs(fft(x))/L; X1 = abs(fft(x1))/L; X2 = abs(fft(x2))/L; % Obtendo os plots dos sinais no dominio do tempo e domínio da frequencia figure(1); subplot(211);plot(time,x, 'b', time,x1, 'g', time, x2, 'r'); legend('x(n)', 'x(n)+rand', 'x(n)awgn', 'Location','south') xlabel('Tempo (seg)'); ylabel('Magnitude (linear)'); subplot(212);plot(freq, (abs(X)), 'b'); hold on ;plot(freq, (abs(X1)),'g');plot(freq,(abs(X2)),'r'); legend('X(f)', 'X(f)+rand', 'X(f)+awgn', 'Location','south'); hold off; xlabel('Frequencia (Hz)'); ylabel('Magnitude (linear)');

• Filtros Digitais (Experimento 2.3)

• Consulte a documentação do Matlab sobre

   fft, ifft, fftshift, randn
  

• Consulte a documentação do Matlab sobre

   plot, grid, subplot, hold, xlabel, ylabel, title, legend, xlim, ylim, log10, log
  

• Consulte a documentação do Matlab sobre text, zp2tf, tf2zp, fftfilt, awgn
• Ver pag. 141 a 145 e 230 a 235 de

Aula 4 - 5 (20 - 24 Fev)

• Revisão de Sinais e Sistemas no tempo discreto em Matlab:

• Filtros Digitais

%% Experimento 2.3 - Filtros Digitais
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
% FILE: Exp2_3.m
 
%% 1º filtro
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 ]'; P = [p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
 
%% 2º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.9*exp(1j*pi/4);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p1 p1' p1 p1']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);
 
%% 3º filtro
z1 = exp(1j*pi/8);
z2 = exp(1j*3*pi/8);
p1 = 0.99*exp(1j*pi/4);
p2 = 0.9*exp(1j*pi/4 - 1j*pi/30);
p3 = 0.9*exp(1j*pi/4 + 1j*pi/30);
Z = [1 -1 z1 z1' z2 z2']';
P = [p1 p1' p2 p2' p3 p3']';
[num,den] = zp2tf(Z,P,1);
[h,w] = freqz(num,den);
figure(1); plot(w,abs(h)/max(abs(h)));
figure(2); zplane(num,den);

• Exercício - Sinal DTMF com ruído

• Verifique se o Matlab está reproduzindo corretamente o som.

%% Carregando o som
clear, close, clc
load handel;

%% Reproduzindo o som 
sound(y,Fs)
 
% Reproduzindo o som 
%soundsc(y,Fs)
 
% Reproduzindo o som 
%player = audioplayer(y, Fs);
%play(player);

• Usando o Matlab (ou Audacity) para gerar um sinal DTMF correspondente a um número N e adicionar um ruido ao sinal. Opcionalmente utilize um sinal DTMF gravado
• Utilizar uma frequência de amostragem de 8000Hz de fazer a duração do sinal igual a 2 segundos.
• Para adicionar o ruído utilize a função y = awgn(x,snr), ou y = x + nivel*randn(n).

• Observe este sinal no domínio do tempo (DT) e domínio da frequência (DF).

%% Carregando o som
clear, close, clc
[y,Fs] = audioread('DTMF_8kHz.ogg');

%% Reproduzindo o som 
sound(y,Fs)

%% Visualizando o som no DT
time = [0:length(y)-1]'/Fs;
plot(time',y'); xlabel('segundos');
xlim([0 time(end)]), ylim([-1 1]);

%% Visualizando o som no DF
Nfreq = length(y);
freq = linspace(0,2*pi,Nfreq)'*Fs/pi/2;
Y = fft(y,Nfreq)/Nfreq;
plot(freq,abs(Y)); xlabel('Hertz');
xlim([0 Fs/2]);

• Filtrar o sinal resultante mantendo apenas a frequência da linha (ou coluna)
• Mostrar os sinais no domínio do tempo e da frequência.

x1,X1 - soma das duas senoides.

x2,X1 - soma de x1 com o ruído branco (gaussiano)

y,Y - sinal filtrado.

• Para a filtragem:

• faça a filtragem no domínio do tempo, usando a função filter posicionando o polo sobre a frequência que deseja passar, e coloque um zero sobre a frequência que deseja rejeitar.
• faça a filtragem no domínio da frequência, convertendo o sinal x1 para DF usando X1 = fft(x1), Y = X1.*H, y = ifft(Y), onde H é um vetor de zeros e uns que indica as frequências que devem passar e quais devem ser rejeitadas.

VER (Experimento 3.1, Experimento 3.2, Experimento 2.3)

Aula (3 Mar)

• 1ª defesas de TCC do Curso de Engenharia de Telecomunicações.

• Alunos assistiram a defesa no auditório das 10:00 as 12:35

Unidade 2

Aula 7 (6 Mar)

• Filtros Analógicos:

• Função de transferência

$H(s)={\frac {c_{0}+c_{1}s+c_{2}s^{2}+...+c_{m}s^{m}}{d_{0}+d_{1}s+d_{2}s^{2}+...+d_{n}s^{n}}},m\leq n$

• Resposta em frequência: para obter a resposta em frequência é necessário avaliar

$H(j\omega )=H(s)\left|{\begin{matrix}\\s=j\omega \end{matrix}}\right.$

$H(j\omega )=\left|H(j\omega )\right|e^{j\phi (\omega )}$

$\left|H(j\omega )\right|^{2}=H(j\omega )H(-j\omega )$

$e^{j\phi (\omega )}={\frac {H(j\omega )}{H(-j\omega )}}$

• O projeto de filtros analógicos é realizado em 2 etapas:

1. projeto de um filtro passa baixas (LP) protótipo normalizado $H(p)$ com frequência de passagem $\Omega _{s}=1$
2. transformação em frequência para o tipo de filtro (LP, HP, BP ou BS)

$H(s)=H(p)\left|{\begin{matrix}\\p=g(s)\end{matrix}}\right.$

Aula 8 e 9 (10 e 13 Mar)

• Projeto de filtros analógicos do tipo Butterworth

• A aproximação de magnitude de filtros analógicos pode ser realizado usando as aproximações de Butterworth, Chebyshev (tipo 1 ou 2) e Cauer.

• Projeto de filtros analógicos do tipo Butterworth, considerando: $\omega _{p}$ é a frequência de passagem do filtro LP, $A_{p}$ é a atenuação em dB na frequência de passagem, $\omega _{s}$ é a frequência de stopband do filtro, $A_{s}$ é a atenuação em dB na frequência de stopband, $\epsilon ={\sqrt {10^{0.1A_{s}}-1}}$, $\Omega _{s}={\frac {\omega _{s}}{\omega _{s}}}$, $\Omega _{p}={\frac {\omega _{p}}{\omega _{s}}}=1$ são as frequências de passagem e stopband do filtro protótipo.

• É necessário determinar a ordem $n$ do filtro:

$n\geq {\frac {\log[(10^{0.1A_{s}}-1)/(10^{0.1A_{p}}-1)]}{2\log \Omega _{s}}}$

• Em seguida obter os polos do filtro:

$p_{k}=\epsilon ^{(-1/n)}e^{\left[j{\frac {(2k+n-1)}{2n}}\pi \right]},k=1,2,3,...n$

• Em seguida é necessário obter a função de transferência:

$H(p)={\frac {1}{D(p)}}$, onde $D(p)=\prod _{k-1}^{n}\left(p-p_{k}\right)$

• No caso de um filtro LP é necessário ainda obter a função de transferência do filtro especificado

$H(s)=H(p)\left|{\begin{matrix}\\p={\frac {s}{\omega _{p}}}\end{matrix}}\right.$

• Ver pag. 186 a 204 de

Aula 10 (17 Mar)

• Projeto de filtros analógicos do tipo Chebyshev I.

• Determine a ordem mínima necessária:

$n\geq {\frac {\cosh {-1}{\sqrt {(10^{0.1A_{s}}-1)/(10^{0.1A_{p}}-1)}}}{\cosh ^{-1}\Omega _{s}}}$

• Em seguida obter os polos do filtro:

$p_{k}=-\sinh(\varphi _{2})\sin(\theta _{k})+j\cosh(\varphi _{2})\cos(\theta _{k})\ \ \ \ \ k=1,2,3,...n$, onde

$\theta _{k}=\left({\frac {(2k-1)\pi }{2n}}\right)$

$\varphi _{2}={\frac {1}{n}}\sinh ^{-1}\left({\frac {1}{\epsilon }}\right)$

• Ver pag. 204 a 208 de

Aula 11 (20 Mar)

• Filtros Analógicos:

• Uso das funções buttord, butter, cheb1ord, cheby1, cheb2ord, cheby2, ellipord, ellip para o projeto de filtros analógicos com Matlab (é necessário usar o parâmetro 's').
• Ler Comparison of Analog IIR Lowpass Filters em ellip
• Uso das funções freqs, "zplane", fvtool na análise da resposta em frequência de filtros analógicos.

• Exemplos de projeto de filtro passa-baixas com frequência de passagem de 16000 rad/s com atenuação máxima de 0.3 dB, frequência de rejeição de 20000 rad/s com atenuação mínima de 20 dB; e ganho em DC de 3 dB.

%% Projeto de filtro passa-baixas usando funções do Matlab  
%% Especificações do filtro 
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
 
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');

%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');

%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');

%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');

• Transformação de frequência de filtros analógicos

(passa-baixas -> passa-baixas, passa-baixas -> passa-altas, passa-baixas -> passa-faixa, passa-baixas -> rejeita-faixa)

$\Omega _{S}=\omega _{s}/\omega _{p}$

• Uso das funções semilogx, semilogy,logspace, linspace.
• Ver em IIR Filter Design,

• Funções para projeto do filtro protótipo analógico passa-baixas: besselap, buttap, cheb1ap, cheb2ap, ellipap
• Funções de transformação de frequencia: lp2bp, lp2bs, lp2hp, lp2lp

• Ver pag. 208 a 218 de

Aula 12 e 13 (24 e 27 Mar)

• Filtros Digitais: Filtros IIR: transformações do tempo contínuo no tempo discreto

• Transformação invariante ao impulso (pode ser usada apenas para filtros com forte atenuação em frequência altas, ex: passa-baixas e passa-faixa)
• Transformação bilinear (pode ser usada para todos tipos de filtro)
• Ver pag. 219 a 229 de
• Ver pag. 403 a 415 e 434 a 435 de

Aula 14 a 16 (31 Mar a 7 Abr)

• Filtros Digitais: Filtros IIR: Uso do Matlab.

• Ver as funções de discretização usadas no Matlab: bilinear, impinvar

• Ver em IIR Filter Design
• Uso das funções buttord, butter, cheb1ord, cheby1, cheb2ord, cheby2, ellipord, ellip para o projeto de filtros IIR digitais (sem o parâmetro 's').

O projeto dos filtros digitais IIR baseados na transformada bilinear no Matlab é realizada em dois passos: (1) Determinação da ordem do filtro; (2) Determinação dos coeficientes do numerador $b(n)$ e denominador $a(n)$ de $H(z)$ .

• Outros tipos de filtros IIR: yulewalk, iirnotch, iirpeak, iircomb,filtfilt, maxflat, invfreqz e outros filtros de modelagem paramétrica.

Unidade 3

Aula 17 (10 Abr)

• Filtros Digitais: Filtros FIR

• Filtros de fase linear: simétricos e antisimétricos (Tipo 1, 2, 3 e 4)
• Filtros de fase linear: propriedades (respostas em frequencia possíveis, distribuição dos zeros em simetria quadrantal)
• Ver pag. 249 a 256 de
• Ver FIR Filter Design

Aula 18 (17 Abr)

• Projeto de FILTRO IIR

• Atividade a distância, com laboratório liberado para uso dos alunos para a realização da AE2.

Aula 19 (24 Abr)

• Filtros Digitais: Filtros FIR:

• Coeficientes da série de Fourier de filtros ideias: LP, HP, BP, BS

• Passa-baixas (Low-pass)

$c_{\text{LP}}(n)=\left\{{\begin{matrix}{\frac {\omega _{c}}{\pi }};&\qquad n=0\\{\frac {\sin(\omega _{c}n)}{\pi n}};&\qquad \left|n\right|>0\end{matrix}}\right.$

• Passa-altas (High-pass)

$c_{\text{HP}}(n)=\left\{{\begin{matrix}1-{\frac {\omega _{c}}{\pi }};\qquad n=0\\-{\frac {\sin(\omega _{c}n)}{\pi n}};\qquad \left|n\right|>0\end{matrix}}\right.$

• Passa-faixa (Band-pass)

$c_{\text{BP}}(n)=\left\{{\begin{matrix}{\frac {\omega _{c2}-\omega _{c1}}{\pi }};\qquad n=0\\{\frac {\sin(\omega _{c2}n)-\sin(\omega _{c1}n)}{\pi n}};\qquad \left|n\right|>0\end{matrix}}\right.$

• Rejeita-banda (Band-stop)

$c_{\text{BS}}(n)=\left\{{\begin{matrix}1-{\frac {\omega _{c2}-\omega _{c1}}{\pi }};\qquad n=0\\-{\frac {\sin(\omega _{c2}n)-\sin(\omega _{c1}n)}{\pi n}};\qquad \left|n\right|>0\end{matrix}}\right.$

• Janela retangular, fenômeno de Gibbs
• Estudar no Matlab as funções wintool, wvtool, window

• Uso de funções de janelamento temporal no projeto de filtros digitais.
• Tipos de janelas temporais usadas no projeto de filtros digitais.

• Retangular

$w(n)=1;\qquad -M\leq n\leq M$

• Bartlett

$w(n)=1-{\frac {\left|n\right|}{M+1}};\qquad -M\leq n\leq M$

• Hanning

$w(n)=0.5+0.5\cos \left({\frac {2\pi n}{2M+1}}\right),-M\leq n\leq M$

• Hamming

$w(n)=0.54+0.46\cos \left({\frac {2\pi n}{2M+1}}\right);\qquad -M\leq n\leq M$

• Blackman

$w(n)=0.42+0.5\cos \left({\frac {2\pi n}{2M+1}}\right)+0.08\cos \left({\frac {4\pi n}{2M+1}}\right);\qquad -M\leq n\leq M$

• em todas as janelas $w\left(n\right)=0$ quando $\left|n\right|\geq M$

onde $M$ é $N/2$ para $N$ par e $(N+1)/2$ para $N$ impar

• Filtros Digitais: Filtros FIR
• Projeto de filtro FIR utilizando janelas temporais
• Uso de janelas fixas no Matlab : rect, triang, bartlett, hann, hamming, blackman, blackmanharris, nuttall.

L = 64; 
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));

Tabela 5.1

Janela	$A_{sl}$	$A_{s}$	$\Delta \omega$
Retangular	13.3	20.33	0.92$\pi$/M
Triangular	26.6	27.41
Bartlett	26.5	27.48
Hann	31.5	44.03	3.11$\pi$/M
Bartlett-Hanning	35.9	40.77
Hamming	42.5	54.08	3.32$\pi$/M
Bohman	46.0	51.84	7.01$\pi$/M
Parzen	53.1	56.89
Backman	58.1	75.25	5.56$\pi$/M
Flat Top	88.0	106.3
Backman-Harris	92.1	108.8
Nutfall	93.8	109.7

• Dados acima obtidos para um filtro passa baixas de ordem N = 64 com $\omega _{c}=0.5\pi$
• Ver pag. 256 a 265 de

(28 Abr)

• Adesão a Greve Geral

Aula 21 (5 Mai)

• Filtros Digitais: Filtros FIR
• Projeto de filtro FIR utilizando janelas temporais fixas.

• Exemplo de projeto

Projetar um filtro passa baixas usando uma janela temporal fixa.
wp = 0.2*pi; Ap = 0.2 dB; Gp = 0 dB
ws = 0.3*pi; As = 60 dB;

Use como uma estimativa inicial os valores da Tabela 5.1 pag. 268

• PASSO 1 - Escolher o tipo de janela de acordo com a atenuação do lóbulo lateral Asl e As.
• PASSO 2 - Estimar a ordem N1 do filtro considerando os parâmetros Dw
• PASSO 3 - Calcule os coeficientes clp do filtro LP , calcule os valores da janela w e obtenha a resposta ao impulso do filtro h = clp * w.
• PASSO 4 - Verifique o valor real de Dwr = wAs-wAp, e faça a correção da ordem do filtro em função do desvio constatado. N2 = N*Dwr/Dw.
• PASSO 5 - Corrija o valor de projeto dos coeficientes Clp do filtro ideal, a janela e a resposta ao impulso.
• Repita o PASSO 3 até 5, até obter um filtro que atenda as especificações de Dw.
• PASSO 6 - Desloque a frequência de corte wc de modo a obter o valor correto de wp. wc2 = wp + (wp-wAp).

• Projeto de filtro FIR.

• Projete os dois filtros projetados anteriormente como IIR, utilizando 3 janelas diferentes. Compare os filtros obtidos com os filtros IIR.

Aula 22 (8 Mai)

• Filtros Digitais: Filtros FIR
• Projeto de filtro FIR utilizando janelas temporais

• Uso de janelas ajustáveis no Matlab: kaiser, chebyshev, gauss, tukey, taylor.

L = 64; 
r = 60;    % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));

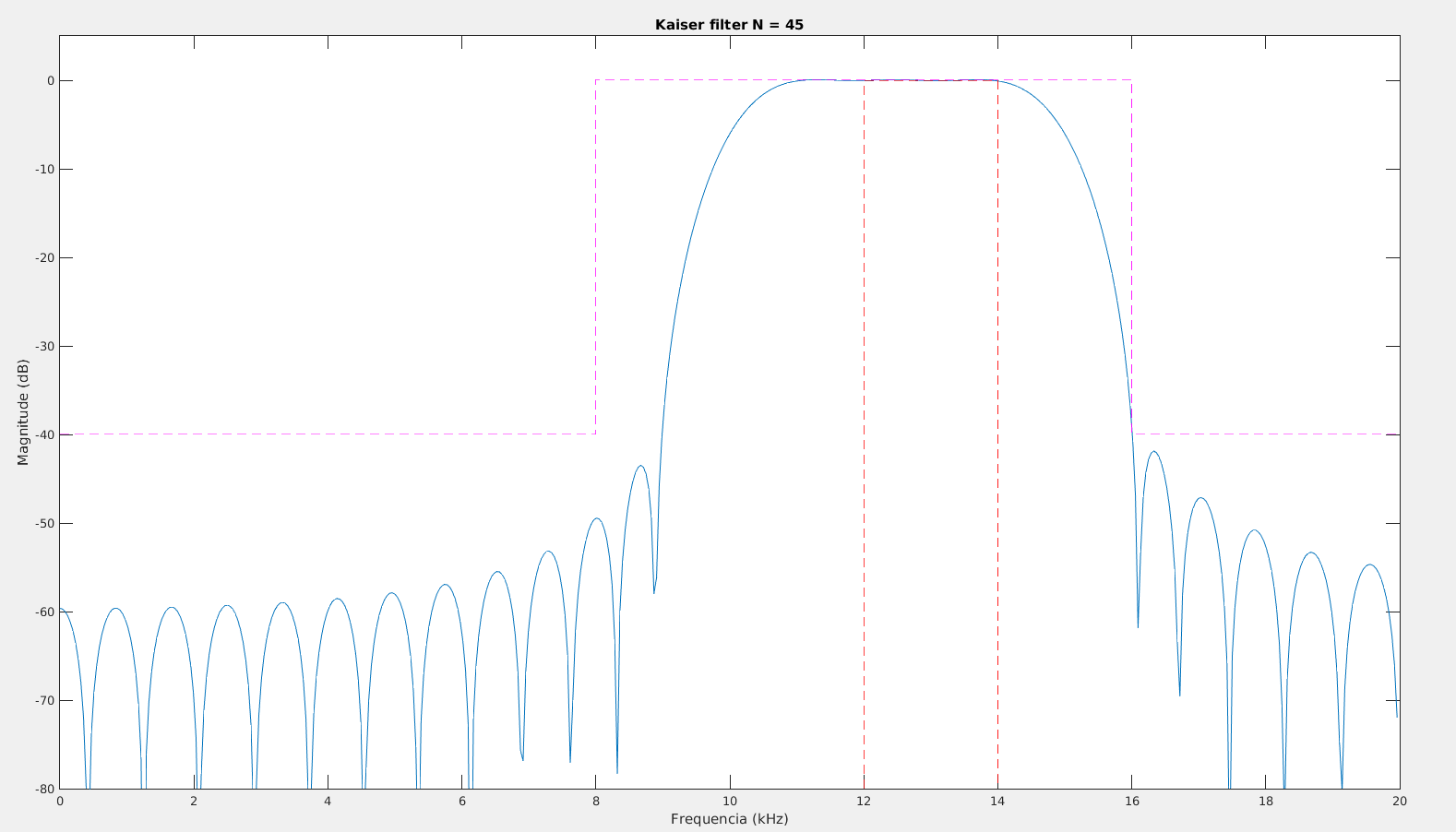
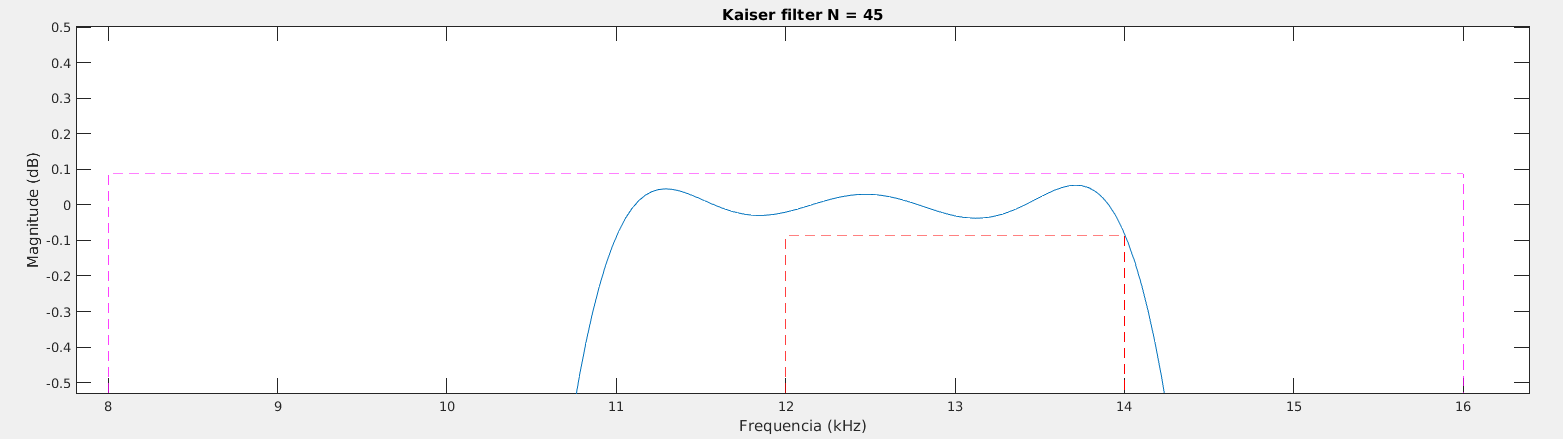
Para a janela de Kaiser, a estimação do fator $\beta$ e da ordem do filtro $N$ são obtidos por:

$\beta =\left\{{\begin{matrix}0.1102(\alpha -8.7),&\alpha >50,\\0.5842(\alpha -21)^{0.4}+0.07886(\alpha -21),&50\geq \alpha \geq 21,\\0,&\alpha <21.\end{matrix}}\right.$

$N={\frac {\alpha -8}{2.285\Delta \omega }}+1.$

onde $\alpha$ é a atenuação do lóbulo lateral e $\Delta \omega$ é a largura da banda de transição em rad/amostra.

Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com $f_{pass}=1000Hz$, $f_{stop}=1500Hz$, $f_{amostragem}=8000Hz$ atenuação de 40 dB na "stopband"

fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.01 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);

Com os parâmetros é possível projetar o filtro usando a função fir1, que utiliza o método da janela para o projeto do filtro.

h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[Hw,w] =freqz(h_fir);
plot(w*fsamp/2/pi,20*log10(abs(Hw)))
title(['Kaiser filter N = ' num2str(n)])
%fvtool(h_fir,1)

• Ver as funções fir1, kaiserord do Matlab.
• Ver pag. 266 a 273 de

Aula 23 (12 Mai)

• Filtros Digitais: Filtros FIR

• Uso das funções window e fir1 do Matlab para projeto de filtro FIR

%% Exemplo de Filtro wp1 = 0.1 \pi; ws1 = 0.2 \pi; ws2 = 0.6 \pi; wp2 = 0.8 \pi; Ap = 1 dB; Ar = 40 dB; </syntaxhighlight>

• Filtro de Parks-McClellan. Funções firpm e firpmord.

Aula 24 (15 Mai)

• Uso do [1] Fdatool para projeto de filtro IIR, FIR equiripple e FIR com janela.

%% Exemplo de Filtro 
fp = 3000 Hz;
fr = 4000 Hz;
fs = 20000 Hz;
Ap = 1 dB;
Ar = 40 dB;

Aula 25 (19 Mai)

• Atraso de grupo em filtros IIR e FIR no Matlab

• O atraso de grupo de um filtro é a medida da atraso médio do filtro em função da frequência do sinal de entrada. Ele é obtido pela primeira derivada da resposta de fase do filtro. Se a resposta em frequencia é $H(e^{j\omega })$ , então o atraso de grupo é:

$\tau _{g}(\omega )={\frac {d\theta (\omega )}{d\omega }}$

onde $\tau _{g}(\omega )$ é a fase de $H(e^{j\omega })$.

• Função para o cálculo do atraso de grupo (group delay) no Matlab
• Compensação do atraso introduzido pelo filtro IIR.
• Filtragem digital com fase nula.
• Compensação do atraso introduzido pelo filtro FIR.

• Um filtro sem distorção de fase (Não causal) pode ser obtido ao passar uma sequencia x(n) por um filtro H1, tomando a saída do filtro revertida e passando novamente pelo mesmo filtro H1. A saída do último filtro revertida corresponde ao sinal x(n) filtro com fase zero. O filtro obtido desta forma tem as seguintes características:

• A Distorção de fase nula
• A função de transferência do filtro é igual a magnitude ao quadrada da função de transferência original do filtro H1.
• A ordem do filtro é o dobro da ordem do filtro H1.

• Exemplo de aplicação a filtragem de um sinal ECG com ruído Arquivo:Noisyecg.txt noisyecg.mat:

%% Carregando um sinal de ECG com ruído com duração de 4 segundos.
load noisyecg.mat
x = noisyECG_withTrend;
fa = 500;  %% 2000 amostras em 4 segundos => 500 amostras por segundo.
t = [0:length(x)-1]*1/fa;
plot(t,x);

%% Projetando um filtro passa-baixa tipo IIR  butter com f_passagem = 0.15 rad/s
d = designfilt('lowpassiir', ...
    'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
    'PassbandRipple',1,'StopbandAttenuation',60, ...
    'DesignMethod','butter');
freqz(d)

%% Filtro de x revertido x e somando com x filtrado. OFF LINE
y = flip(filter(d,flip(filter(d,x))));
y1 = filter(d,x);

figure(2);
subplot(2,1,1)
plot(t, [y y1])
title('Filtered Waveforms')
legend('Zero-phase Filtering','Conventional Filtering')

subplot(2,1,2)
plot(t, [x y])
title('Original Waveform')
legend('noisy ecg ','fitered ecg')

• Verifique também o resultado da filtragem usando um filtro IIR (ellip, cheby1 ou cheby2) e filtros FIR (equiripple e de janela)

%% Projetando um filtro passa-baixa tipo FIR  equiripple com f_passagem = 0.15 rad/s
d = designfilt('lowpassfir', ...
    'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
    'PassbandRipple',1,'StopbandAttenuation',60, ...
    'DesignMethod','equiripple');

y = flip(filter(d,flip(filter(d,x))));

• Note que nos filtros FIR de fase linear o procedimento mais simples é adiantar o sinal de acordo com o atraso de grupo (metade da ordem do filtro), devendo-se tomar cuidado para arredondar a meia amostra nos filtros de ordem impar.

y1 = filter(d,x);
gd = grpdelay(d);
gd1 = ceil(gd(1));
y = [y1(gd1:end); zeros(gd1-1, 1)];

O cálculo do atraso de grupo pode ser realizado utilizando a função grpdelay ou diretamente pela definição da derivada do ângulo em relação a frequência:

$\tau _{g}(\omega )={\frac {d\theta (\omega )}{d\omega }}=\lim _{\Delta _{\omega }\to 0}{\frac {\theta (\omega +\Delta _{\omega })-\theta (\omega )}{\Delta _{\omega }}}$

%% Calculo do atraso de grupo usando a função grpdelay
[z,p,k] = butter(30,0.2);
sos = zp2sos(z,p,k);
[gd,w]=grpdelay(sos,128);
figure(1)
plot(w/pi,gd),grid on;

• Ler Gustafsson, F. "Determining the initial states in forward-backward filtering." IEEE® Transactions on Signal Processing. Vol. 44, April 1996, pp. 988–992, artigo que propos um técnica de minimizaçao dos transientes de inicio e fim do sistema linear.

Unidade 4

Aula 26 (22 Mai)

• Realização de Filtros

• Realização de filtros FIR: Forma Direta.

Figura 1 - Realização de filtros FIR na Forma Direta

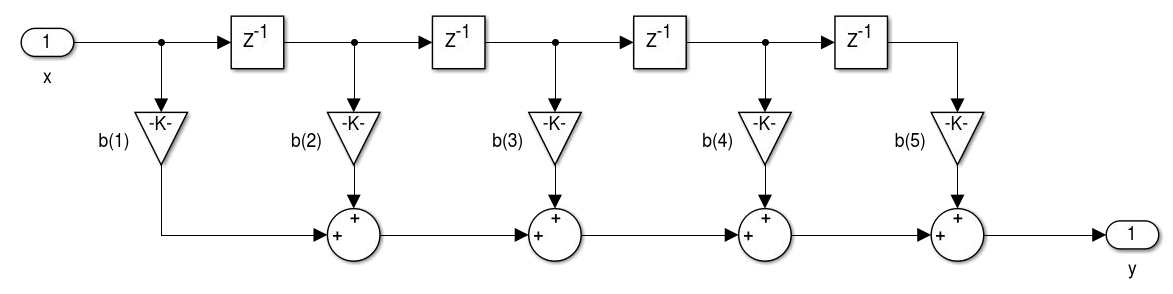
• Realização de filtros FIR: Forma Transposta. A transposição consiste na inversão do fluxo de todos os sinais, substituição de nós de soma por derivações e as derivações por soma. A entrada e saída também devem ser invertidas. A realização da transposição não altera o sistema implementado.

Figura 2 - Realização de filtros FIR na Forma Transposta Figura 3 - Realização de filtros FIR na Forma Transposta

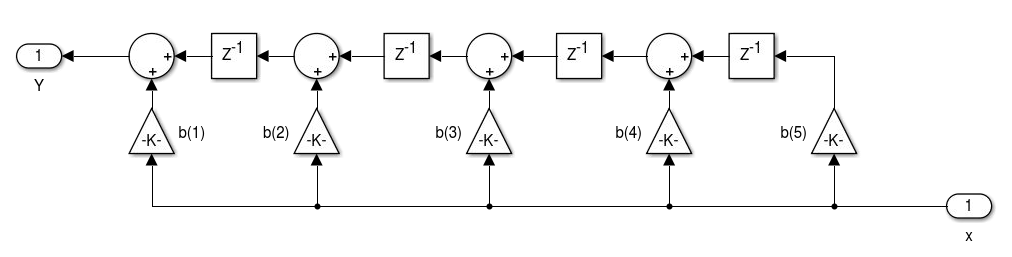
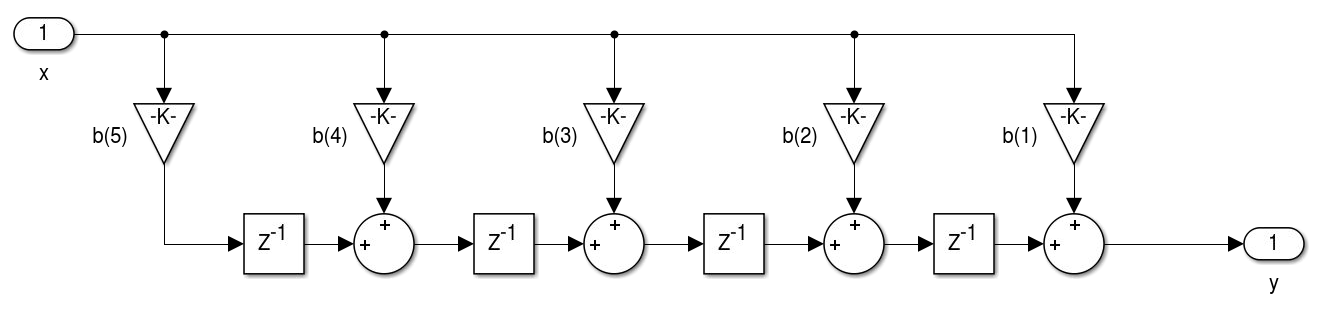
• Realização de filtros FIR de fase linear: simétrico tipo I e II e antissimétrico tipo III e IV.

Figura 4 - Realização de filtros FIR de fase linear Simétrico I Figura 5 - Realização de filtros FIR de fase linear Simétrico II Figura 6 - Realização de filtros FIR de fase linear Antisimétrico III Figura 7 - Realização de filtros FIR de fase linear Antisimétrico IV

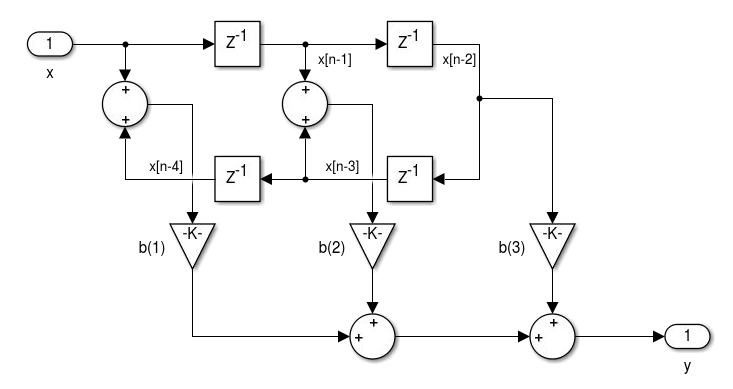
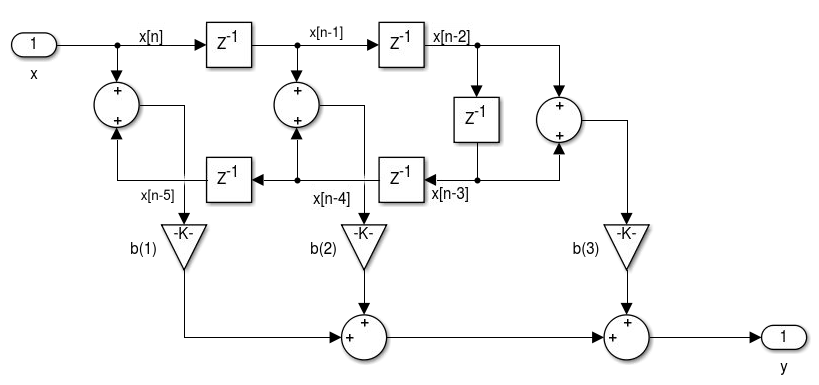
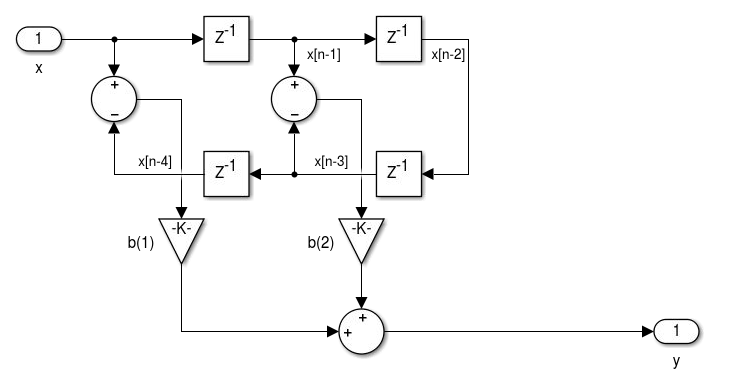
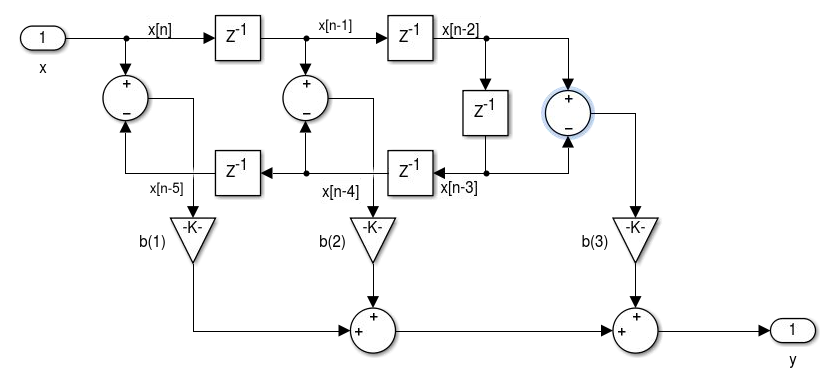
• Realização de Filtros FIR usando o FDATool

• Estudar estrutura de filtros disrcetos FIR no Matlab, Filter Realization Wizard - Reference, Filter Realization Wizard - User Guide.
• Ver pag. 303 a 312 de .

Aula 27 (26 Mai)

• Realização de Filtros usando o comando realizemdl do MatLab

Fs = 30000;              % Sampling Frequency
Fpass = 12000;           % Passband Frequency
Fstop = 13000;           % Stopband Frequency
Dpass = 0.01;            % Passband Ripple
Dstop = 0.01;            % Stopband Attenuation
flag  = 'scale';         % Sampling Flag

% Calculate the order from the parameters using KAISERORD.
[N,Wn,BETA,TYPE] = kaiserord([Fpass Fstop]/(Fs/2), [1 0], [Dstop Dpass]);

% Calculate the coefficients using the FIR1 function.
b  = fir1(N, Wn, TYPE, kaiser(N+1, BETA), flag);

hFIR = dsp.FIRFilter;
hFIR.Numerator = b;

% Para definir diretamente os coeficientes
realizemdl(hFIR)

% Para definir os coeficientes através de uma matriz de entrada
realizemdl(hFIR,'MapCoeffsToPorts','on');

• Realização de filtros FIR: Cascata, Polifase

• Vantagens do uso de filtro Polifase:

1) Quando o sinal será subamostrado (downsampling) de "D" amostras após a filtragem, a complexidade da implementação é reduzida de "D" vezes, pois apenas uma das "fases" precisa ser implementada.

2) Para reduzir o harware a ser implementado, é possível implementar apenas uma das "fases" do filtro e trocar "D" vezes os coeficientes.

• Ver polyphase, mfilt.firdecim, dsp.FIRDecimator

• Realização de filtros IIR de 2ª ordem: Forma Direta I e II, e Forma Transposta I e II.

$H(z)={\frac {Y(z)}{X(z)}},H(z)={\frac {b_{0}z^{2}+b_{1}z^{1}+b_{2}}{z^{2}+a_{1}z^{1}+a_{2}}},H(z)={\frac {b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1+a_{1}z^{-1}+a_{2}z^{-2}}}$

• Separando H(z) em dois blocos $\ H(z)=H_{1}(z)H_{2}(z)$, e obtendo o sinal intermediário W(z) ou Y(z) dependendo da ordem dos blocos.

Figura 7 - Separação do filtro IIR H(z) em H1(z) e H2(z)

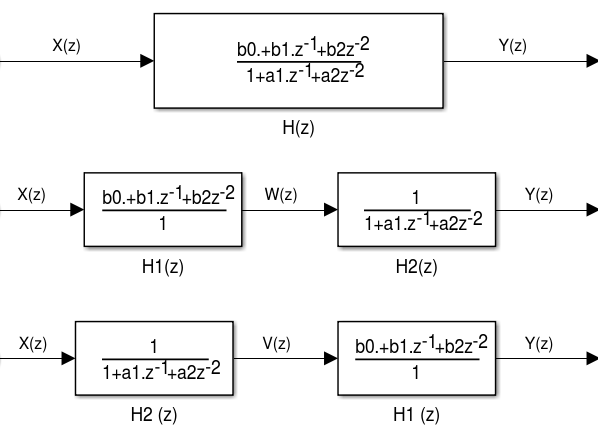
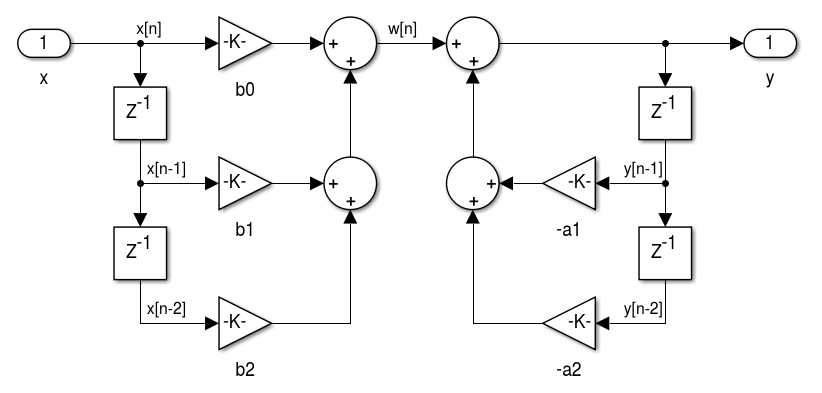
Com o ordenamento dos blocos $\ H_{1}(z)$ e $\ H_{2}(z)$ em ordem direta teremos a Forma Direta I:

$H_{1}(z)={\frac {W(z)}{X(z)}}=b_{0}+b_{1}z^{-1}+b_{2}z^{-2}$

$H_{2}(z)={\frac {Y(z)}{W(z)}}={\frac {1}{1+a_{1}z^{-1}+a_{2}z^{-2}}}$

Podemos obter a realização de $\ H_{1}(z)$ na forma direta.

$\ W(z)=(b_{0}+b_{1}z^{-1}+b_{2}z^{-2})X(z)$

Para obter a realização de $\ H_{2}(z)$ , é necessário reescrever a saída $\ Y(z)$ em função de $\ W(z)$ e das saídas anteriores $\ Y(z)z^{-1}$ e $\ Y(z)z^{-2}$:

$\ Y(z)={\frac {W(z)}{1+a_{1}z^{-1}+a_{2}z^{-2}}}$

$\ Y(z)({1+a_{1}z^{-1}+a_{2}z^{-2}})=W(z)$

$\ Y(z)=W(z)-a_{1}Y(z)z^{-1}-a_{2}Y(z)z^{-2}$

Figura 8 - Realização de filtros IIR na Forma Direta I

Com o ordenamento dos blocos $\ H_{2}(z)$ e $\ H_{1}(z)$ em ordem reversa teremos a Forma Direta II:

$H_{2}(z)={\frac {V(z)}{X(z)}}={\frac {1}{1+a_{1}z^{-1}+a_{2}z^{-2}}}$

$\ V(z)=X(z)-a_{1}V(z)z^{-1}-a_{2}V(z)z^{-2}$

$H_{1}(z)={\frac {Y(z)}{V(z)}}=b_{0}+b_{1}z^{-1}+b_{2}z^{-2}$

$\ Y(z)=(b_{0}+b_{1}z^{-1}+b_{2}z^{-2})V(z)$

Figura 9 - Realização de filtros IIR na Forma Direta II

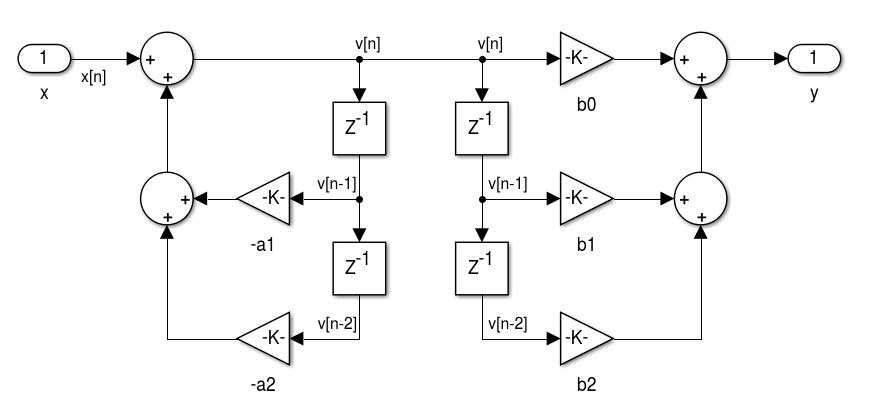
Considerando que os sinais no centro são idênticos podemos simplificar e obter a Forma Direta II (Canônica):

Figura 10 - Realização de filtros IIR na Forma Direta II Canônica

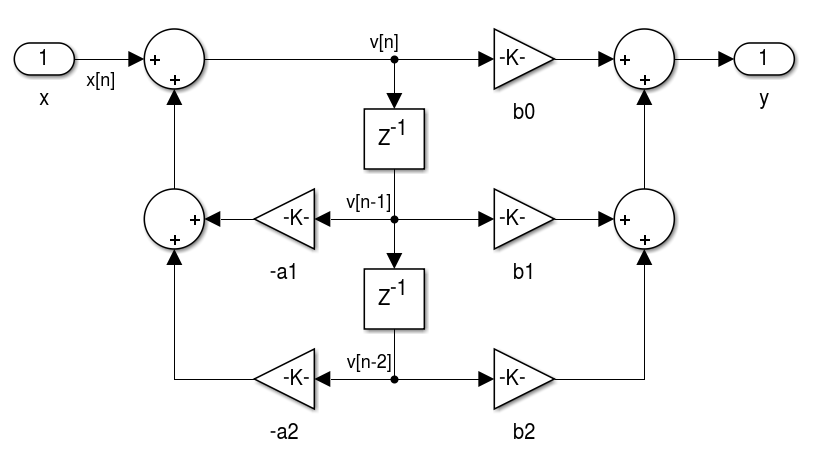
Considerando as regras de transposição podemos obter a forma transposta I e II. A transposição consiste na inversão do fluxo de todos os sinais, substituição de nós de soma por derivações e as derivações por soma. A entrada e saída também devem ser invertidas. A realização da transposição não altera o sistema implementado.

Figura 11 - Realização de filtros IIR na Forma Transposta I Figura 12 - Realização de filtros IIR na Forma Transposta II

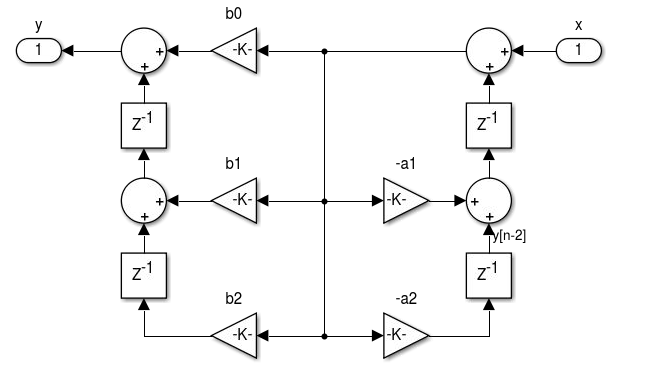
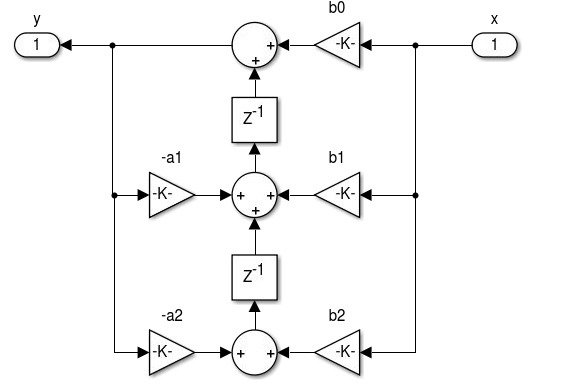
• Realização de filtros IIR de ordem maior que 2: Forma Direta I e II, Transposta I e II, Cascata, Paralela

• Os filtros IIR de ordem superior a 2 podem ser implementados nas FD I ou II e na FT I ou II. No entanto nessa configuração tendem a ficar instáveis ao terem os coeficientes quantizados, e também terem uma significativa alteração da resposta em frequência. Para reduzir esses problemas uma possível solução é a decomposição em filtros de 2ª ordem para serem associados na forma em Cascata ou Paralela.

• Ver Biquad Filter
• Ver funções do Matlab: roots, poly, residuez, tf2zp, zp2tf, zp2sos, tf2sos, tf2latc.
• Implementar o exercício 6.3: Forma direta I, Forma direta II, Cascata.
• Implementar o exercício 6.13: Forma direta I, Cascata e Paralela.
• Ver pag. 313 a de 353 .
• Ver pag. 469 a 474 do Lathi

• Filtros Digitais: Ferramentas do Matlab para projeto

• Practical Introduction to Digital Filter Design
• Filter Design Gallery
• Função para projeto de filtros - designfilt

Aula 27 (29 Mai)

• Filtros Digitais: Utilização de filtros FIR

• Utilizar o Audacity para gerar sinais de teste. Gere os seguintes sinais e analise seus espectrogramas:

• Um sinal DTMF com duração de 1 segundo com frequência de amostragem de 8 kHz, correspondente aos dígitos 1234567890 ('Dtmf.wav').
• Um sinal contendo ruído branco com duração de 5 segundo com frequência de amostragem de 8 kHz ('RuidoBranco.wav').
• Um sinal onda quadra com duração de 2 segundo com frequência de amostragem de 8 kHz e período de 2 ms ('Quadrada.wav').

Utilize o Matlab para gerar o seguinte sinal:

• Um sinal de varredura de Cosseno entre 0 Hz e 4 kHz com duração de 1 segundo.

Fs = 8000;
t = 0:1/Fs:1-1/Fs;
x = chirp(t,0,1,4000);
spectrogram(x, blackman(128), 120, 200, Fs,'yaxis')
audiowrite('Chirp0-4kHz.wav',x,Fs)
sound(x,Fs)  % Atenção remova o fone de ouvido antes de realizar este procedimento.

Utilizar o Matlab para projetar os seguintes filtros FIR e transmitir os sinais obtidos acima. Em todos os filtros considere a frequência de amostragem como 8 kHz, atenuação máxima na banda de passagem de 0,5 dB, e as bandas de transição como 400 Hz. Use a janela de Kaiser.

• Filtro passa-baixas com fc = 1,5 kHz e atenuação de 60 dB na rejeição;
• Filtro passa-altas com fc = 2,5 kHz e atenuação de 30 dB na rejeição;
• Filtro passa faixa com fc1 = 1,5 kHz e fc2 = 2,5 kHz e atenuação de 80 dB na rejeição;
• Filtro rejeita faixa com fc1 = 1,9 kHz e fc2 = 2,1 kHz e atenuação de 80 dB na rejeição;

Após obter os filtros, transmita cada um dos sinais gerados no Audacity através do filtro e verifique o resultado obtido analisando os sinal obtidos comparando o espectrograma com a resposta em magnitude do filtro.

[x, Fs] = audioread('Chirp0-4kHz.wav');  % Leitura do sinal
t = (0:length(x)-1)/Fs;  % Vetor de tempo
b = fir1(48,[2000 2100]/Fs); % Filtro Hamming com ordem 48 passa faixa

sound(x,Fs)  % Atenção remova o fone de ouvido antes de realizar este procedimento.
y = filter(b,1,x);
sound(y,Fs)  % Atenção remova o fone de ouvido antes de realizar este procedimento.
subplot(311); spectrogram(x, blackman(128), 100, 200, Fs)
subplot(312); spectrogram(y, blackman(128), 100, 200, Fs)
[Hw, w] = freqz(b,1,2000);
subplot(313); plot(w/pi*Fs/2,20*log10(abs(Hw))); ylim([-100,0]);

• Ver as funções audioread, audiowrite, chirp, spectrogram, filter do Matlab.

Aula 29 (2 Jun)

• Filtros Digitais: Quantização

• Ver Fixed-Point Filter Properties

Ver Use Filter Designer with DSP System Toolbox Software

x=-0.2;
% Word length = 8, fraction length = 7
q=quantizer([8,7]);
xq=quantize(q,x);
binxq=num2bin(q,xq)
% Word length = 16, fraction length = 15
q1=quantizer([16 15]); 
xq1 = quantize(q1,x);
binxq1=num2bin(q1,xq1)

Unidade 5 - PROJETO FINAL

Aula 30 (5 Jun)

• Apresentação do projeto Final

• Descrição do projeto AE5 - Projeto de um Detector de DTMF

Aula 31 (9 Jun)

• Uso do Simulink

• Uso dos blocos de simulação sinewave, scope e Spectrum Analyzer.
• Outros blocos mux, demux, sum, product.
• Create Simple Model [2]

Aula 32 (12 Jun)

• Uso do Simulink
• Tipos de Solver (Choose a Solver).
• Diferença entre processamento por amostra e processamento por quadro (Sample- and Frame-Based Concepts).
• Exemplos:

• Filtragem - frame based
• Modulações Analógicas
• Amostragem de sinais
• Digital Filter Design Block, [3], [4]

• É importante ler informações complementares sobre o Solver Pane, Model Simulation, Types of Solvers, Solvers for Discrete-Event Systems.

• É importante ler informações complementares sobre, Tempo de amostragem (Time Sample), View Sample Time Information, Vector Concatenate, Matrix Concatenate

Para configurar o Simulink para sistemas discretos execute o comando dspstartup.m antes de abrir um novo modelo.

Aula 33 (19 Jun)

• Aula de projeto (implementação da AE5)

Aula 34 (23 Jun)

• Uso do HDL Coder

• HDL Code Generation from Simulink
• Simulink® blocks supported for HDL code generation

• Exemplo simples.

• Inicialmente construa a biblioteca de blocos suportados pelo HDLcoder

hdllib  Show Blocks Supported for HDL Code Generation

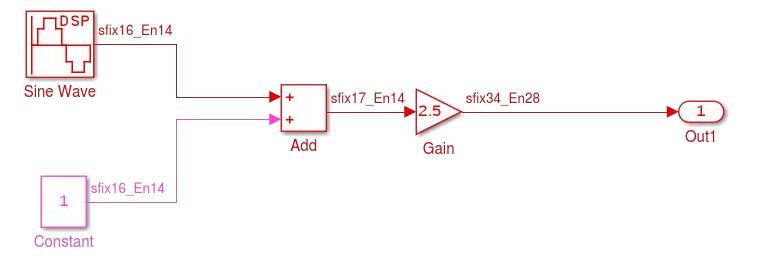
• Construa o modelo mostrado na figura abaixo. (sugestão de frequência do sinal de 100Hz, e frequência de amostragem deve ser de 1000Hz)

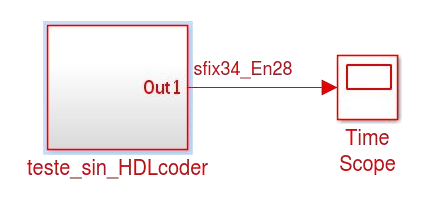
• coloque o modelo em um subsistema e conecte a saída a um Time Scope

• Salve o modelo como teste_sin_HDLcoder, e em seguida faça o ajuste automático das configurações usando o comando.

hdlsetup('teste_sin_HDLcoder')

• Execute o HDLcoder
• Siga o fluxo do HDLcoder passo a passo e corrija eventuais problemas conforme indicado nas mensagens de ERRO.

• Será necessário mudar o tipo de dado do bloco seno e constante para fix(16).

• Após ter concluído com sucesso o fluxo de codificação HDL, vá até a pasta onde os arquivos VHDL foram gerados e observe que devem ser sido gerados os seguintes arquivos (Subsystem_tb_pkg.vhd Subsystem_tb.vhd Subsystem.vhd) na pasta

cd  hdl_prj/hdlsrc/teste_sin_HDLcoder
ls *.vhd

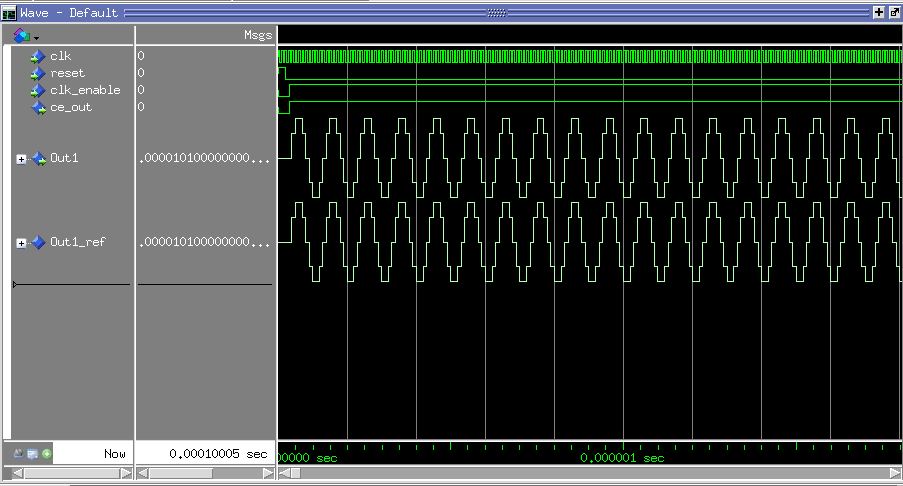
• Use o ModelSim para compilar os arquivos e em seguida simular

vsim &

• No ModelSim execute os seguintes arquivos .do:

Subsystem_compile.do
Subsystem_tb_compile.do
Subsystem_tb_sim.do

• Observe que o sinal gerado pelo código VHDL é igual ao sinal calculado pelo Simulink.

• Observe que no arquivo de testbench, existe uma instrução de ASSERT conferindo se os dois sinais são iguais:

IF Out1_testFailure = '0' THEN
 ASSERT FALSE
 REPORT "**************TEST COMPLETED (PASSED)**************"
 SEVERITY NOTE;
ELSE
 ASSERT FALSE
 REPORT "**************TEST COMPLETED (FAILED)**************"
 SEVERITY NOTE;
END IF;

• Exemplo mais complexo

• Abra o modelo

sfir_fixed

• ajuste as configurações

hdlsetup('sfir_fixed')

• Siga o tutorial HDL Code Generation from a Simulink Model

Aula 35 a 37 (26 Jun a 3 Jul)

• Implementação do projeto final.

Avaliações

• Entrega dos diversos trabalhos ao longo do semestre.
• Projeto Final. O projeto é avaliado nos quesitos:

1) Implementação do Sistema,

2) Documentação,

3) Avaliação Global do aluno no projeto.

Neste tópico serão listadas as atividades avaliativas que os alunos da disciplina deverão realizar ao longo do curso.

AE1 - Revisão de Sinais e Sistemas (prazo 03/Mar/2017 as 23h59)

- sem atribuição de conceitos. No Experimento 1.2 Varie o valor da frequência de amostragem de 6 até 20 Hz e observe: Em qual frequência deixa de ocorrer recobrimento do sinal 2. O que ocorre quando a frequência é 6, 7, 14 Hz? Explique Qual deveria ser a frequência do sinal f_2 para que as amostras tomadas sejam coincidentes como o sinal f_1 para uma frequência de amostragem f_s? Reescreva a equação e verifique no Matlab. No Experimento 2.2 Verifique a diferença entre os tipos de plots comentados no código. substitua o denominador de H(z) por dois polos em [-0.8 -0.8]. verifique o que ocorre se forem utilizados polos complexos conjugados [0.3-0.4i 0.3+0.4i 0.1] verifique o que ocorre se forem utilizados polos complexos não conjugados [0.3-0.4i 0.3+0.8i] verifique o que ocorre se os polos estiverem fora do circulo unitário [1.2 -0.2]. Interprete este resultado No Experimento 3.1 Utilizando Nh = 10 e Nx = 20, execute a filtragem pelo menos 3 vezes em seguida e anote os tempos. Anote o tamanho dos sinais de saída y, e analise os plots. Aumente o tamanho do filtro (Nh) e o tamanho do sinal de entrada (Nx) e execute a filtragem pelo menos 3 vezes em seguida e anote os tempos. Anote o tamanho dos sinais de saída y. Explique os resultados obtidos. No Experimento 3.2 Acrescente um subplot para mostrar o sinal no domínio da frequência com a magnitude em dB 20*log10(abs(X)). Limite a escala da magnitude entre -100 e 1 dB usando ylim. Insira em todos os plots e subplot, títulos, legendas e labels para os eixos X e Y, Posicione o texto "F Hz" para indicar o pico nos gráficos 2 e 3, conforme mostrado na figura abaixo. Figura 1 - Análise no domínio da frequência do sinal $x(t)=Asin(2\pi ft)$ Varie o valor de k entre 0 e 2 (com passo de 0.1) e analise o sinal no domínio do tempo e no domínio da frequência. Varie o valor de snr entre 100 e 1 e analise o sinal no domínio do tempo e no domínio da frequência. Utilize k = 0.3 e snr = 40 e varia a frequência do sinal entre 0 até 200 Hz (com passo de 10 Hz). Interprete os resultados obtidos. Utilizando o espectro de frequência (Exp3.2) repita as medições feitas com o processo de amostragem (Exp1.2) Qual conclusão que você chega em relação a amostragem de sinais utilizando para a frequência de amostragem valores acima e abaixo do dobro da frequencia de Nyquist. Para analisar o espectro talvez seja conveniente mudar a amplitude dos sinais de entrada. Faça um relatório (em pdf) incluindo as principais figuras obtidas e as respostas e conclusões para o email "moecke at ifsc.edu.br" com o Assunto: PSD29007 - AE1 - Revisão de Sinais e Sistemas.

AE2 - Projeto de Filtros Digitais IIR (Entrega e prazos ver Moodle)

Esta avaliação visa verificar se você conhece a metodologia de projeto de filtros digitais IIR: (a) projeto de um filtro protótipo analógico passa-baixas H(p); (b) transformação em frequência do filtro H(p) -> H(s), obtendo o filtro LP, HP, BP, BS, conforme o tipo de filtro desejado; (c) transformação do filtro analógico em filtro digital H(s) -> H(z) utilizando a transformação "Bilinear" ou pela transformação "Invariante ao Impulso". Nesta avaliação é solicitado que cada equipe realize o projeto de dois filtros. Equipe Filtro 1 Filtro 2 Equipe 1 LP - (f1 = 30 kHz; f2 = 50 kHz, fa = 200 kHz, Gp = 10 dB, Ap = 1 dB, As = 50 dB) BS - (f1 = 30 kHz; f2 = 32 kHz, f3 = 33 kHz; f4 = 35 kHz, fa = 100 kHz) Equipe 2 HP - (f1 = 30 kHz; f2 = 50 kHz, fa = 300 kHz, Gp = 2 dB, Ap = 0.2 dB, As = 40 dB) BP - (f1 = 30 kHz; f2 = 32 kHz, f3 = 33 kHz; f4 = 35 kHz, fa = 200 kHz) Equipe 3 HP - (f1 = 10 kHz; f2 = 14 kHz, fa = 50 kHz, Gp = -10 dB, Ap = 1 dB, As = 45 dB) BS - (f1 = 10 kHz; f2 = 20 kHz, f3 = 30 kHz; f4 = 50 kHz, fa = 200 kHz) Equipe 4 LP - (f1 = 10 kHz; f2 = 14 kHz, fa = 44 kHz, Gp = 5 dB, Ap = 2 dB, As = 60 dB) BP - (f1 = 30 kHz; f2 = 100 kHz, f3 = 200 kHz; f4 = 220 kHz, fa = 500 kHz) Equipe 5 HP - (f1 = 50 MHz; f2 = 120 MHz, fa = 500 MHz, Gp = 12 dB, Ap = 0.1 dB, As = 80 dB) BS - (f1 = 50 kHz; f2 = 100 kHz, f3 = 180 kHz; f4 = 220 kHz, fa = 500 kHz) Equipe 6 LP - (f1 = 120 kHz; f2 = 200 kHz, fa = 500 kHz, Gp = -5 dB, Ap = 0.3 dB, As = 50 dB) BS - (f1 = 60 kHz; f2 = 100 kHz, f3 = 150 kHz; f4 = 220 kHz, fa = 1 MHz) Equipe 7 HP - (f1 = 120 kHz; f2 = 160 kHz, fa = 400 kHz, Gp = 1 dB, Ap = 0.5 dB, As = 60 dB) BP - (f1 = 6 kHz; f2 = 8.2 kHz, f3 = 14 kHz; f4 = 20 kHz, fa = 200 kHz onde: LP (Low Pass)- Passa Baixa, HP (High Pass)- Passa Altas, BP (Band Pass)- Passa Faixa, BS (Band Stop)- Rejeita Faixa $f_{N}$ - são as "N" frequência de especificação do filtro dadas em Hertz (kHz ou MHz); f_a é a frequência de amostragem dos sinais e do sistema. $f_{p}$ - frequência de passagem; $f_{r}$ - frequência de rejeição, $A_{p}$ - Atenuação máxima na banda de passagem (dB), $A_{r}$ - Atenuação mínima na banda de rejeição (dB), $G_{p}$ - Ganho médio na banda de passagem (dB). No 1º filtro os valores das frequência de passagem e rejeição são: para LP $f_{p}=f_{1}$, $f_{r}=f_{2}$, para HP $f_{r}=f_{1}$, $f_{p}=f_{2}$. Os valores de ganhos e atenuações estão indicados na tabela. No 2º filtro os valores das frequência de passagem e rejeição são: para BP $f_{p1}=f_{2}$ e $f_{p2}=f_{3}$, $f_{r1}=f_{1}$ e $f_{r2}=f_{4}$, para BS $f_{p1}=f_{1}$ e $f_{p2}=f_{4}$, $f_{r1}=f_{2}$ e $f_{r2}=f_{3}$. No segundo filtro os valores de ganhos e atenuações são de Gp = 0 dB, Ap = 1 dB, As = 40 dB. Um dos filtros deve ser realizado utilizando a aproximação de Butterworth ou Chebyshev tipo 1 (devendo ser todos os calculados efetuados a partir das equações), enquanto o outro filtro deve ser feito utilizando a aproximação de Chebyshev tipo 2 ou Euler (podendo ser calculada a função H(p) a partir das funções do Matlab. Para ambos filtros deve indicada a ordem do filtro, o valor de polos e zeros, e as equações de H(p), H(s), H(z). Deve ser apresentado de forma gráfica a resposta em frequência dos filtros (ganho em dB e fase) dos filtros (a) protótipo H(p), (b) Filtro analógico H(s) e Filtro digital H(z). Para mostrar que os filtros atendem a especificação. No caso do filtro H(z) também deve ser mostrado o atraso de grupo (ver função grpdelay do Matlab) Apresente o diagrama dos pólos e zeros dos filtros H(p), H(s) e H(z) Utilize a mesma escala em dB para os 3 gráficos de cada filtro. Nas abcissas utilize uma escala em Hz (kHz ou MHz). Utilize uma mascara com cor diferenciada para indicar claramente a especificação do filtro, e crie um segundo gráfico mostrando claramente a banda de passagem conforme ilustrado nas figuras abaixo: Escreva um relatório técnico em PDF mostrando os resultados obtidos e comentando os resultados obtidos. Não é necessário apresentar a teoria utilizado para o projeto, mas todos os cálculos e metodologia utilizada devem estar documentados. O "Publish" pode ser utilizado, mas o arquivo entregue deve ser PDF. Envie o relatório em pdf e os arquivos ".m" utilizados na plataforma Moodle.

AE3 - Projeto de Filtros Digitais FIR (Entrega e prazos ver Moodle)

Esta avaliação visa verificar se você conhece a metodologia de projeto de filtros digitais FIR: (a) Projeto de filtros com Janela Fixas e Ajustáveis; (b) Projeto de filtros com o algoritmo de Parks-McCleallan; Nesta avaliação é solicitado que cada equipe realize os mesmo dois projeto de filtros da atividade AE2. O primeiro filtro deve ser realizado utilizando uma janela fixa calculando os valores dos coeficientes da série de Fourier, os valores do vetor da janela podem ser obtidos usando as funções do Matlab. O filtro também deve ser projetado usando uma das janelas ajustáveis. O segundo filtro deve ser realizado utilizando uma janela fixa e uma ajustável, podendo ser utilizado diretamente funções do Matlab que projetem o filtro. Neste filtro também deve ser feito o projeto usando o algoritmo de Parks-McCleallan. Para ambos filtros deve indicada a ordem do filtro, o valor de polos e zeros. Procure obter em cada caso a menor ordem que possibilite ter uma resposta de frequência que atende a sua especificação. Deve ser apresentado de forma gráfica a resposta em frequência dos filtros (ganho em dB e fase e atraso de grupo) dos Filtro digital H(z). Apresente o diagrama dos pólos e zeros do filtro H(z) Utilize a mesma escala em dB para os 2 (ou 3 filtros). Nas abcissas utilize uma escala em Hz (kHz ou MHz). Utilize uma mascara com cor diferenciada para indicar claramente a especificação do filtro, e crie um segundo gráfico mostrando claramente a banda de passagem conforme ilustrado nas figuras da atividade AE2. Escreva um relatório técnico em PDF mostrando os resultados obtidos e comentando os resultados obtidos. Não é necessário apresentar a teoria utilizado para o projeto, mas todos os cálculos e metodologia utilizada devem estar documentados. O "Publish" pode ser utilizado, mas o arquivo entregue deve ser PDF. Envie o relatório em pdf e os arquivos ".m" utilizados na plataforma [5].

AE4 - Realização de Filtro Digitais FIR e IIR (Entrega e prazos ver Moodle)

1. Objetivo projetar filtros que tem a a mesma especificação de magnitude usando diferentes tipos de filtro digital, sendo um do tipo IIR e outro do tipo FIR. Estabelecer uma comparação entre esses filtros e escrever um artigo mostrando as vantagens do filtro escolhido sobre o outro. 2. É permitido (incentivado) o uso de ferramentas como o FDAtool e funções como o fdesing para o projeto do filtro. 3. Cada equipe deverá realizar o projeto de um filtro (LP ou HP) e um filtro (BP ou BS), com as especificações dadas na AE2 e AE3. Note que nas atividades AE2 e AE3 os projetos dos filtros foram feitos com precisão infinita (ponto flutuante - 64 bits). Nesta etapa os filtros projetados deverão ser REALIZADOS utilizando no mínimo as seguintes estruturas: IIR - Forma direta I, II (ou as transpostas correspondentes). IIR - Em seções de segunda ordem (SOS). FIR - Forma direta(ou transposta) FIR - Forma (anti)simétrica. 4. A segunda etapa do projeto será com precisão finita (usando ponto fixo), devendo o aluno buscar minimizar a área necessária, considerando tanto a ordem do filtro, como o número de bits necessário. Para fins de simplificação, considere que a área de hardware (AHw) necessária para implementar um filtro corresponde a: $AHw=max((2xN_{multiplicadores}+N_{somadores}),N_{atrasos})*N_{bits}.$ Note que para manter o filtro dentro das especificações talvez seja necessário reprojetar o filtro. Mostre de modo simplificado como o filtro é realizado em cada caso. Indique o valor dos coeficientes após a quantização. Utilize gráficos sobrepostos para comparar a realização dos filtros com diferentes estruturas e quantizações. Utilize uma tabela para resumir os resultados (hardware, ordem, atraso de grupo, número de bits) e compare a implementação usando FIR e IIR. 5. Escreva um relatório mostrando os resultados obtidos e envie o relatório em pdf e os arquivos ".m" utilizados na plataforma [6]

ATUAL

AE5 - Projeto de um Detector de DTMF (Entrega e prazos ver Moodle)

Projeto de um receptor DTMF. cada equipe deverá projetar os discriminadores de frequências correspondente a duas linhas e duas colunas do sistema DTMF. 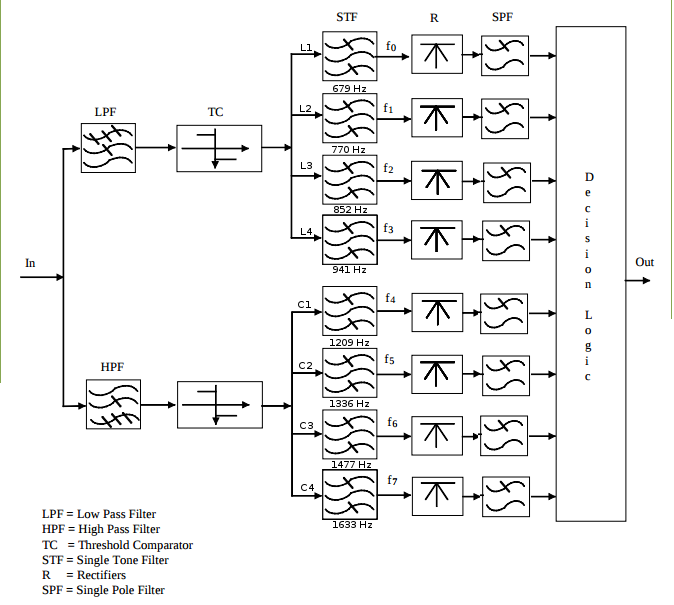Equipe Linhas Colunas Teclas Equipe 1 L1, L4 C2, C3 2, 3, 0, # Equipe 2 L2, L4 C1, C2 4, 5, *, 0 Equipe 3 L1, L3 C1, C3 1, 3, 7, 9 Equipe 4 L1, L2 C2, C3 2, 3, 5, 6 Equipe 5 L3, L4 C1, C2 7, 8, *, 0 Equipe 6 L2, L3 C1, C3 4, 6, 7, 9 Equipe 7 L2, L4 C2, C3 5, 6, 0, # As especificações do discriminador de frequência, mostrado na figura, são: De acordo com ETSI ES 201 235-3 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 3: Receivers as características dos componentes do receptor são: — low-pass filter F <= 960 Hz; — high-pass filter F >= 1190 Hz; — two threshold comparators; — eight channel filters (two pole filters: -1,5 dB band pass limits at the nominal frequency ± (1,5%+ 2 Hz)); — eight rectifiers; — eight single pole (RC) filters, time constant \tau = 4 a 5 ms. The thresholds and decision logic are regulated in order not to recognize character signals with a level below -30 dBm and to recognize valid character signals with a level in the range of -4 dBm to -30 dBm. </syntaxhighlight> A frequência de amostragem f_s do sinal de entrada no sistema mostrado acima é de 8 kHz. O circuito retificador deve se implementado pela função abs. Como sinais de entrada devem com frequência de amostragem de 48kHz e serão utilizados: 1) Os 4 Sinal de DTMF correspondentes as 4 teclas indicadas para a equipe, com duração de 1 segundo 2) Um sinal DTMF correspondente a sequencia de teclas "123456789*0#" com duração de tom de 65ms e pausa de 65ms para cada tecla. (ver ETSI ES 201 235-2 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 2: Transmitters) 3) Os sinais do item (1) e (2) somados a um ruído branco. A seleção do sinal de entrada e adição do ruido pode ser feita através de chaves manuais. Neste projeto os sinais de entrada a serem utilizados deverão ser gerados com frequência de amostragem de 48 kHz. Antes de realizar o processamento indicado no diagrama do receptor DTMF, deve ser feita uma filtragem passa-baixa com um filtro de no mínimo 2 polos do tipo Butterworth ou Chebychev 1, com fc = 0.5*48000/6 = 4kHz, seguido de uma subamostragem para a nova frequência de = 8kHz. A contante de tempo $\mathrm {T} =RC$ é equivalente a uma frequência de corte de $w_{c}=1/(2\pi \mathrm {T} )$ Após realizada a simulação do sistema detector DTMF, o sistema deverá ser convertido para VHDL utilizando o HDL coder. Para comprovar o funcionamento do sistema realize a simulação final do sistema no ModelSim. Escreva um relatório técnico em PDF mostrando os resultados obtidos e comentando os resultados obtidos. Não é necessário apresentar a teoria utilizado para o projeto, mas a metodologia utilizada devem estar documentados. Envie o relatório em pdf e os arquivos de projeto utilizando a plataforma Moodle. ::* (Opcional) As equipes que desejarem poderão programar o hardware de um kit FPGA para conferir o funcionamento do sistema. Sugere-se que a geração dos sinais DTMF seja feita utilizando um app gerador para Smartphone e usada a interface conversora A/D para capturar os sinais de entrada. Ver as especificações DTMF em: ETSI ES 201 235-1 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 1: General ETSI ES 201 235-2 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 2: Transmitters ETSI ES 201 235-3 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 3: Receivers ETSI ES 201 235-4 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 4: Receivers for use in Terminal Equipment for end-to-end signalling

Referências Bibliográficas

Curso de Engenharia de Telecomunicações