PSD29007-Engtelecom(2016-2) - Prof. Marcos Moecke
1 Registro on-line das aulas
1.1 Unidade 1
- Aula 1 (11 Ago)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Resposta de sistemas LTI (Experimento 1.1)
- Relembrar o conceito de equação de diferenças de um sistema LTI discreto e resposta ao impulso.
- Resposta ao delta de Kronecker do sistema LTI discreto
- onde , e logo
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.1
alpha = 1.15; N = 256;
x = [1 zeros(1,N)];
y = filter(1,[1 -1/alpha],x);
stem(y);
- Amostragem de Sinais (Experimento 1.2)
- Relembrar teorema da amostragem. Efeito da amostragem abaixo da frequência de Nyquist. Aliasing.
- Notar que as amostras de um sinal (3 Hz) e um sinal (7 Hz) são idênticas quando amostrado com um sinal de 10 Hz.
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.2
fs = 10; % frequencia (Hz) de amostragem dos sinais
Ts = 1/fs; fase = 0;
time = 0:Ts:(1-Ts);
f1 = 3; % frequencia (Hz) do sinal s_1
f2 = 7; % frequencia (Hz) do sinal s_2
s_1 = cos(2*pi*f1*time+fase);
s_2 = cos(2*pi*f2*time+fase);
fsa = 1000; % frequência auxiliar de amostragem usada apenas para representação dos sinais originais
Tsa = 1/fsa;
time_aux = 0:Tsa:(1-Tsa);
figure(1);
stem(time,s_1,'ob');
hold on;
plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k');
stem(time,s_2,'+r');
plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m');
hold off;
legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo')
- Uso do Matlab: Help, F9 executa o código destacado no Help. Programação com scripts .m, Execução de seções e variação de valores nos scripts,
- Ver no Matlab: zeros, ones, plot, stem, subplot, filter.
- Uso de gráficos no Matlab.
- Ver pag. 65 a 71 de [1]
- Ver também PDF Documentation for MATLAB. Principalmente MATLAB Primer.
- Aula 2 (15 Ago)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
| Variação do Experimento 2.2 |
|---|
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 2.2
% Resposta em frequencia usando a função freqz
N = 1;
num = [1 0 0 0];
den = poly([0.8 0.2])
%den = [1 0.6 -0.16];
% modo 1
%[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]);
%plot(w/pi, abs(H));
% modo 2
%[H,w]=freqz(num,den);
%plot(w/pi, abs(H));
% modo 3
%[H,w]=freqz(num, den, 'whole');
%plot(w/pi, abs(H));
% modo 4
freqz(num, den, 'whole');
figure(2);
zplane(num,den);
%% Resposta em frequencia substituindo z -> e^(jw)
syms z
Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z);
pretty(Hf)
latex(Hf)
N = 1;
w = [0:pi/100:N*pi-pi/100];
plot(w/pi,abs(Hf(exp(1i*w))))
%title(['$' latex(Hf) '$'],'interpreter','latex')
text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex')
xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex')
|
- Aula 3 (18 Ago)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Filtragem de Sinais (Experimento 3.1)
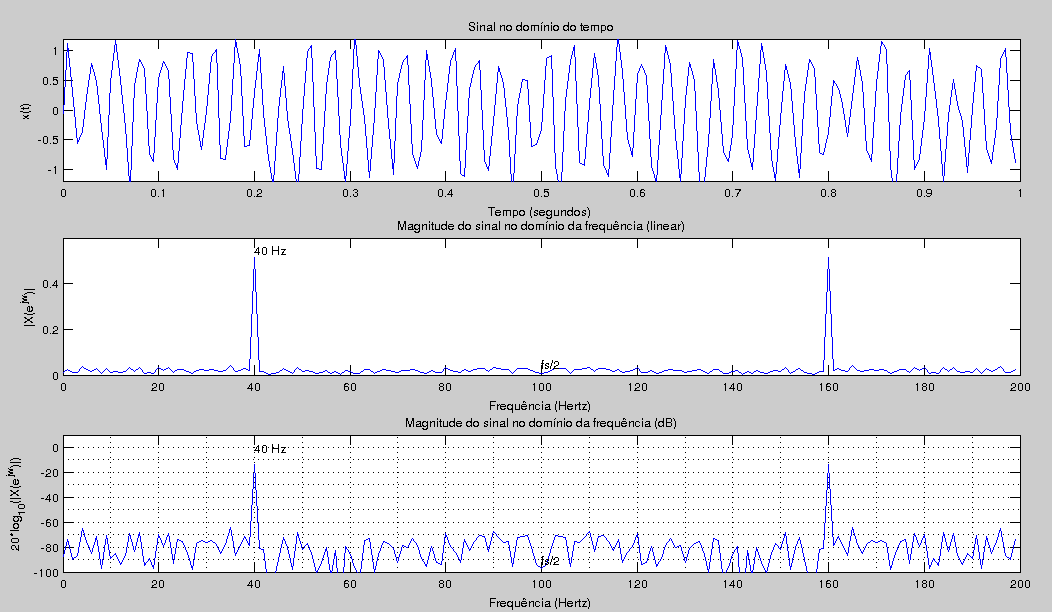
- Análise de Sinais (Experimento 3.2) - Análise de um sistema h[n] correspondente a um filtro passa-faixa, utilizando um sinal de entrada x[n] senoidal (ou um sinal r[n] de ruído branco). Análise da entrada x[n] e saída y[n] usando a fft.
- Aula 4 (22 Ago)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Exercício - Sinal DTMF com ruído
- Usando o Matlab, gerar o sinal DTMF correspondente ao número N e adicionar um ruido ao sinal.
- Filtrar o sinal resultante mantendo apenas a frequência da linha (ou coluna)
- Mostrar os sinais no domínio do tempo e da frequência.
- x1,X1 - soma das duas senoides.
- x2,X1 - soma de x1 com o ruído branco (gaussiano)
- y,Y - sinal filtrado.
- Utilizar uma frequência de amostragem de 8000Hz de fazer a duração do sinal igual a 200 ms.
- Para adicionar o ruído utilize a função y = awgn(x,snr), ou y = x + nivel*randn(n).
- Para a filtragem utilize?
- faça a filtragem no domínio do tempo, usando a função filter posicionando o polo sobre a frequência que deseja passar, e coloque um zero sobre a frequência que deseja rejeitar.
- faça a filtragem no domínio da frequência, convertendo o sinal x1 para DF usando X1 = fft(x1), Y = X1.*H, y = ifft(Y), onde H é um vetor de zeros e uns que indica as frequências que devem passar e quais devem ser rejeitadas.
- VER (Experimento 3.1, Experimento 3.2, Experimento 2.3)
1.2 Unidade 2
- Aula 5 (25 Ago)
- Filtros Analógicos:
- Função de transferência
- Resposta em frequência: para obter a resposta em frequência é necessário avaliar
- O projeto de filtros analógicos é realizado em 2 etapas:
- projeto de um filtro passa baixas (LP) protótipo normalizado com frequência de passagem
- transformação em frequência para o tipo de filtro (LP, HP, BP ou BS)
- A aproximação de magnitude de filtros analógicos pode ser realizado usando as aproximações de Butterworth, Chebyshev (tipo 1 ou 2) e Cauer.
- Projeto de filtros analógicos do tipo Butterworth, considerando: é a frequência de passagem do filtro LP, é a atenuação em dB na frequência de passagem, é a frequência de stopband do filtro, é a atenuação em dB na frequência de stopband, , , são as frequências de passagem e stopband do filtro protótipo.
- É necessário determinar a ordem do filtro:
- Em seguida obter os polos do filtro:
- Em seguida é necessário obter a função de transferência:
- , onde
- No caso de um filtro LP é necessário ainda obter a função de transferência do filtro especificado
- Ver pag. 186 a 204 de [2]
- Aula 6 ()
- Projeto de filtros analógicos do tipo Chebyshev I.
- Determine a ordem mínima necessária:
- Em seguida obter os polos do filtro:
- , onde
- Ver pag. 204 a 208 de [2]
- Aula 7 ()
- Filtros Analógicos:
- Uso das funções buttord, butter, cheb1ord, cheby1, cheb2ord, cheby2, ellipord, ellip para o projeto de filtros analógicos com Matlab (é necessário usar o parâmetro 's').
- Ler Comparison of Analog IIR Lowpass Filters em ellip
- Uso das funções freqs, "zplane", fvtool na análise da resposta em frequência de filtros analógicos.
- Exemplos de projeto de filtro passa-baixas com frequência de passagem de 16 krad/s com atenuação máxima de 0.3 dB, frequência de rejeição de 20 krad/s com atenuação mínima de 20 dB; e ganho em DC de 3 dB.
%% Projeto de filtro passa-baixas usando funções do Matlab
%% Especificações do filtro
Wp =16000; Ws = 20000; Ap = 0.3; As = 20; G0= 3;
% Para analisar o filtro projetado, use fvtool(b,a) para observar plano s, resposta em magnitude, fase e atraso de grupo
%% Butterworth
[n,Wn] = buttord(Wp, Ws, Ap, As,'s')
[b,a] = butter(n,Wn, 's');
%% Chebyshev I
n = cheb1ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby1(n,Ap, Wp, 's');
%% Chebyshev II
n = cheb2ord(Wp, Ws, Ap, As,'s')
[b,a] = cheby2(n,As, Ws, 's');
%% Elliptic - Cauer
[n, Wn] = ellipord(Wp, Ws, Ap, As,'s')
[b,a] = ellip(n,Ap,As, Wn, 's');
1.3 Unidade 3
- Aula 12 ()
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: simétricos e antisimétricos
- Ver pag. 249 a 256 de [2]
- Aula 13 ()
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: propriedades
- Coeficientes da série de Fourier de filtros ideias: LP, HP, BP, BS
- Passa-baixas (Low-pass)
-
- Passa-altas (High-pass)
-
- Passa-faixa (Band-pass)
-
- Rejeita-banda (Band-stop)
- Uso de funções de janelamento temporal no projeto de filtros digitais.
- Tipos de janelas temporais usadas no projeto de filtros digitais.
- Retangular
- Bartlett
- Hanning
- Hamming
- Blackman
- em todas as janelas quando
- Ver pag. 256 a 265 de [2]
- Aula 16 e 17 ()
- Filtros Digitais: Filtros FIR
- Projeto de filtro FIR utilizando janelas temporais
- Uso de janelas fixas no Matlab : rect, triang, bartlett, hann, hamming, blackman, blackmanharris, nuttall.
L = 64;
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));
| Janela | |||
|---|---|---|---|
| Retangular | 13.3 | {{{4}}} | |
| Triangular | 26.6 | {{{4}}} | |
| Barlett | 26.5 | {{{4}}} | |
| Hann | 31.5 | {{{4}}} | |
| Barlett-Hanning | 35.9 | {{{4}}} | |
| Hamming | 42.5 | {{{4}}} | |
| Bohman | 46.0 | {{{4}}} | |
| Parzen | 53.1 | {{{4}}} | |
| Backman | 58.1 | {{{4}}} | |
| Flat Top | 88.0 | {{{4}}} | |
| Backman-Harris | 92.1 | {{{4}}} | |
| Nutfall | 93.8 | {{{4}}} |
L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
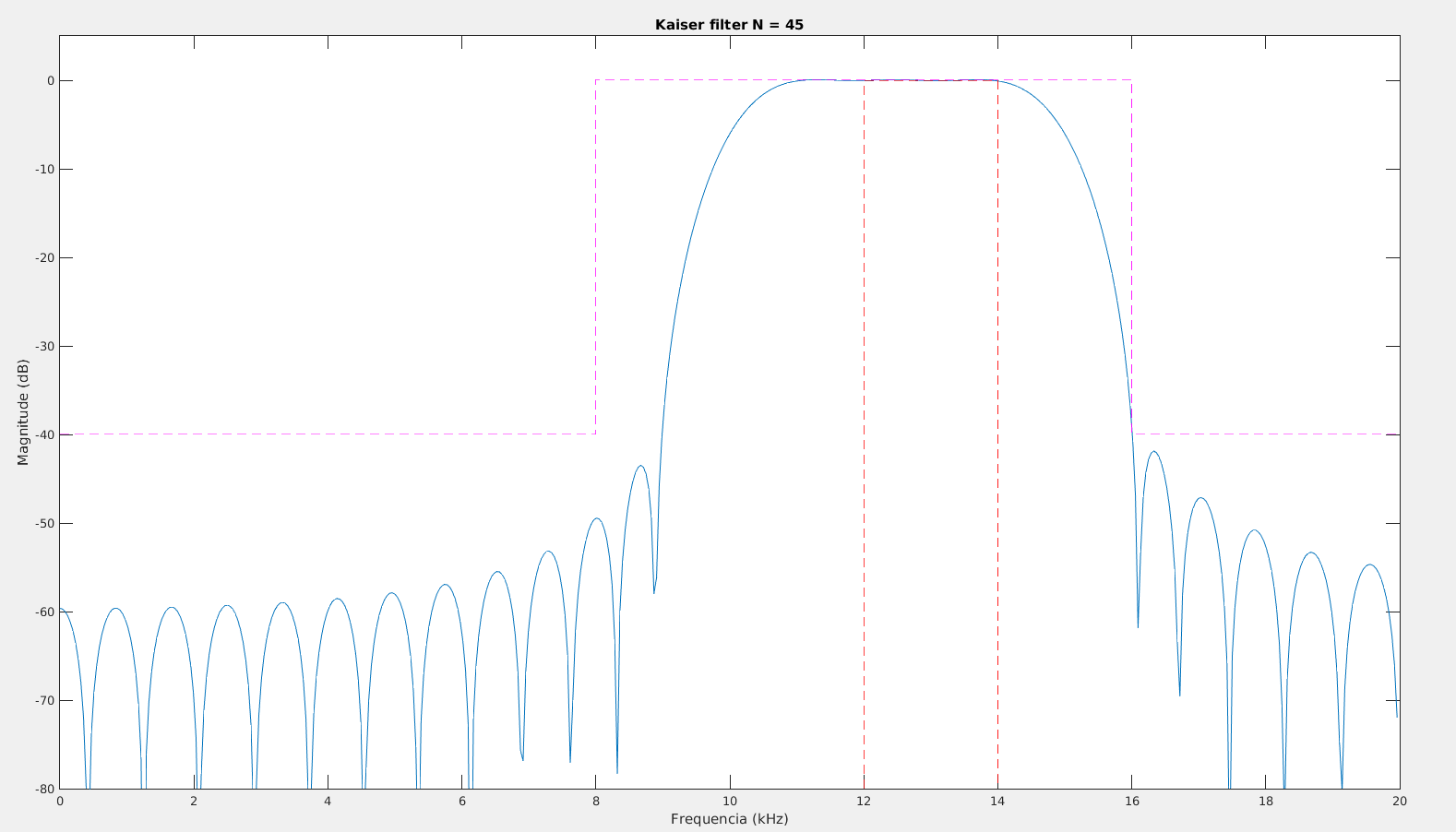
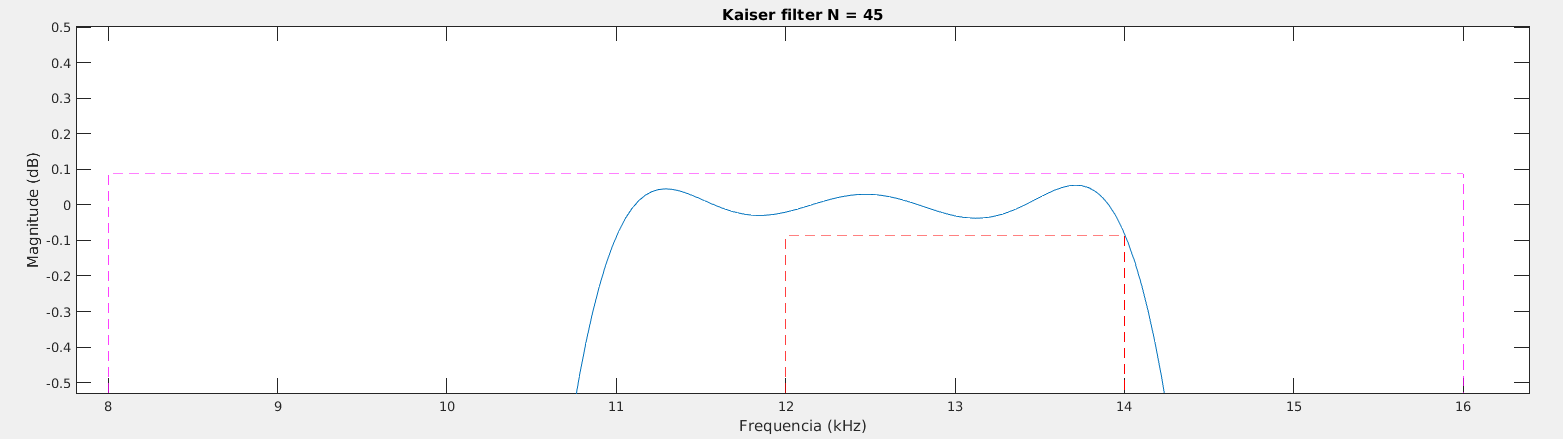
Para a janela de Kaiser, a estimação do fator e da ordem do filtro são obtidos por:
- onde é a atenuação do lóbulo lateral e é a largura da banda de transição em rad/amostra.
Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com , , atenuação de 40 dB na "stopband"
fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.01 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
Com os parâmetros é possível projetar o filtro usando a função fir1, que utiliza o método da janela para o projeto do filtro.
h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[Hw,w] =freqz(h_fir);
plot(w*fsamp/2/pi,20*log10(abs(Hw)))
title(['Kaiser filter N = ' num2str(n)])
%fvtool(h_fir,1)
- Aula 18 ()
- Filtros Digitais: Filtros FIR
%% Exemplo de Filtro wp1 = 0.1 \pi; ws1 = 0.2 \pi; ws2 = 0.6 \pi; wp2 = 0.8 \pi; Ap = 1 dB; Ar = 40 dB; </syntaxhighlight>
- Aula 19 ()
- Filtros Digitais: Filtros FIR
- Aula 20 ()
%% Exemplo de Filtro
fp = 3000 Hz;
fr = 4000 Hz;
fs = 20000 Hz;
Ap = 1 dB;
Ar = 40 dB;
1.4 Unidade 4
- Aula 20 ()
- Realização de Filtros
- Realização de filtros FIR: Forma Direta.
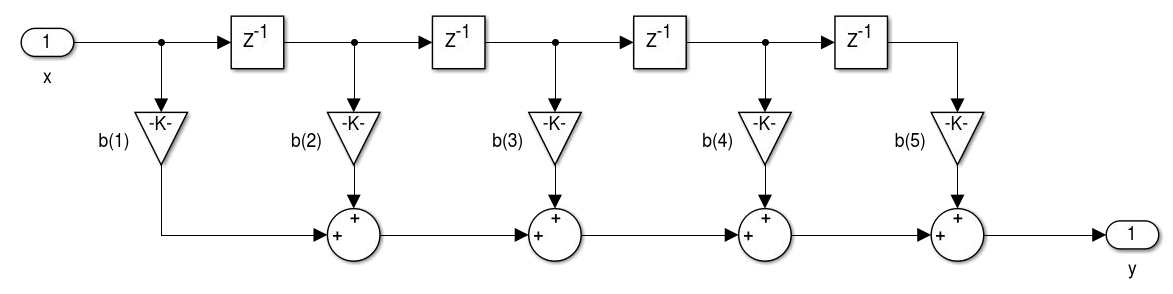
- Realização de filtros FIR: Forma Transposta. A transposição consiste na inversão do fluxo de todos os sinais, substituição de nós de soma por derivações e as derivações por soma. A entrada e saída também devem ser invertidas. A realização da transposição não altera o sistema implementado.
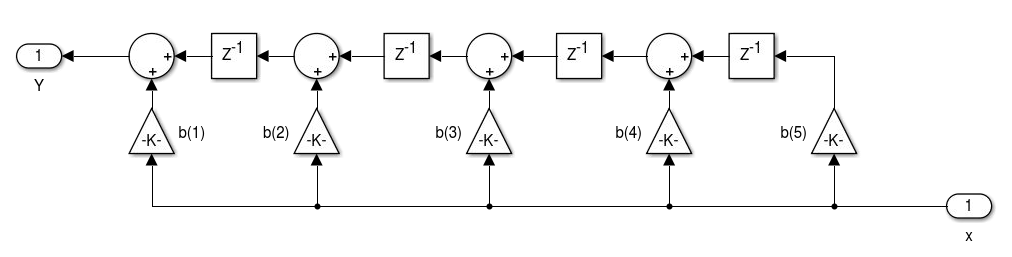
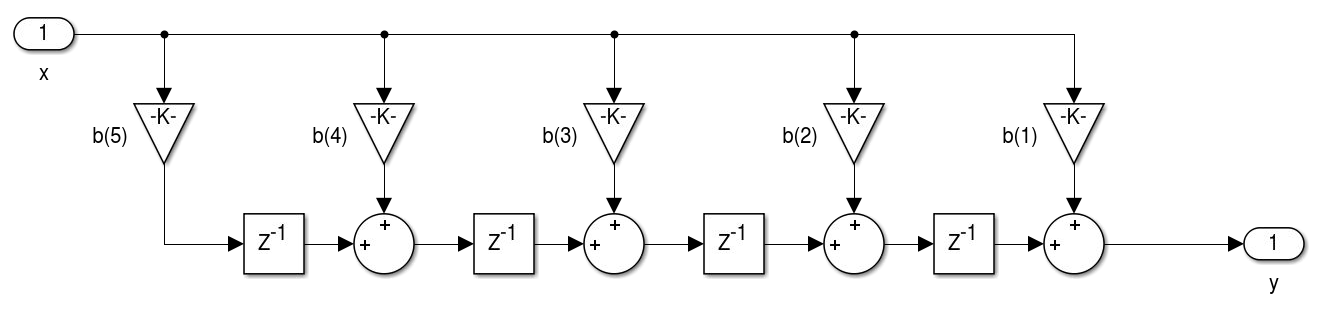
- Realização de filtros FIR de fase linear: simétrico tipo I e II e antissimétrico tipo III e IV.
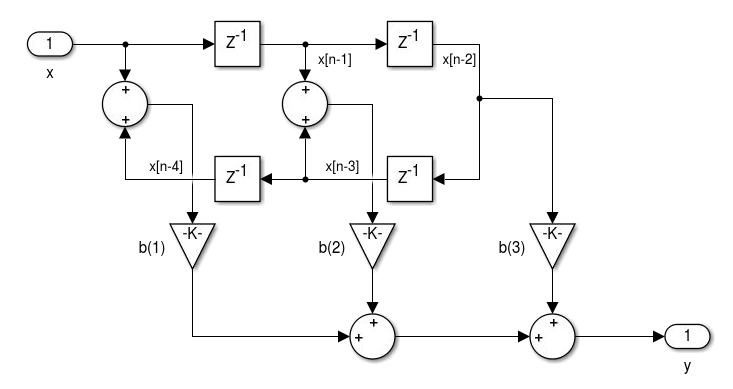
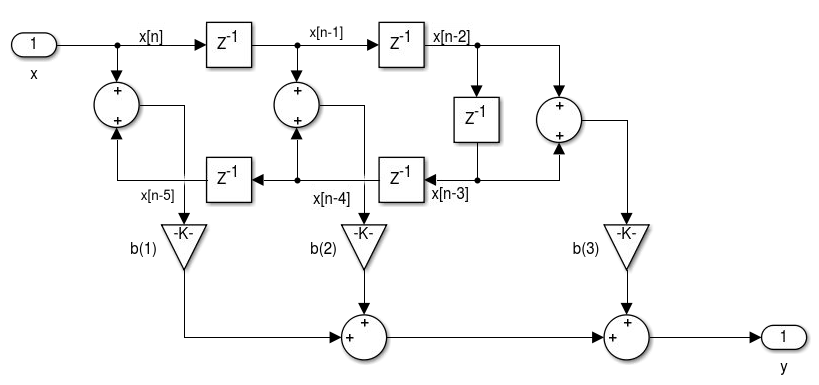
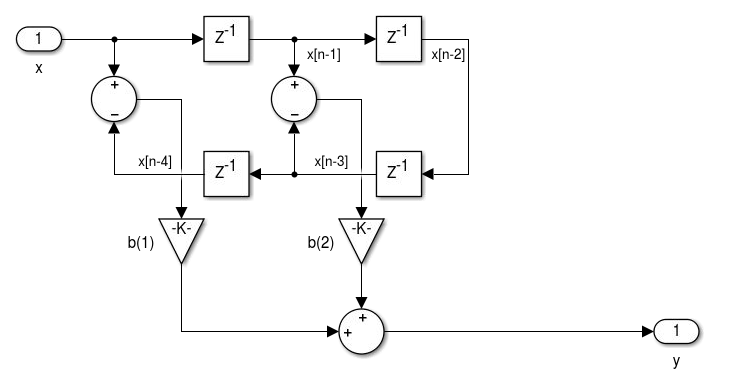
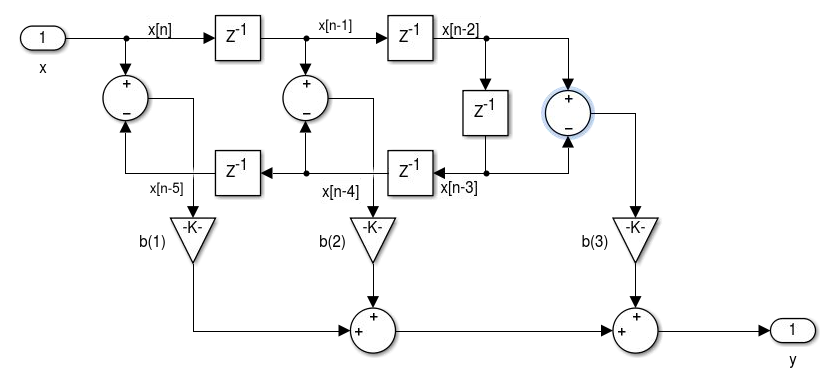
- Realização de Filtros FIR usando o FDATool
- Realização de Filtros usando o comando realizemdl do MatLab
Fs = 40000; % Sampling Frequency
Fpass = 12000; % Passband Frequency
Fstop = 13000; % Stopband Frequency
Dpass = 0.01; % Passband Ripple
Dstop = 0.01; % Stopband Attenuation
flag = 'scale'; % Sampling Flag
% Calculate the order from the parameters using KAISERORD.
[N,Wn,BETA,TYPE] = kaiserord([Fpass Fstop]/(Fs/2), [1 0], [Dstop Dpass]);
% Calculate the coefficients using the FIR1 function.
b = fir1(N, Wn, TYPE, kaiser(N+1, BETA), flag);
hFIR = dsp.FIRFilter;
hFIR.Numerator = b;
% Para definir diretamente os coeficientes
realizemdl(hFIR)
% Para definir os coeficientes através de uma matriz de entrada
realizemdl(Hd,'MapCoeffsToPorts','on');
- Estudar estrutura de filtros disrcetos FIR no Matlab, Filter Realization Wizard - Reference, Filter Realization Wizard - User Guide.
- Ver pag. 303 a 312 de [2].
- Aula 22 ()
- Realização de filtros FIR: Cascata, Polifase
- Vantagens do uso de filtro Polifase:
- 1) Quando o sinal será subamostrado (downsampling) de "D" amostras após a filtragem, a complexidade da implementação é reduzida de "D" vezes, pois apenas uma das "fases" precisa ser implementada.
- 2) Para reduzir o harware a ser implementado, é possível implementar apenas uma das "fases" do filtro e trocar "D" vezes os coeficientes.
- Realização de filtros IIR de 2ª ordem: Forma Direta I e II, e Forma Transposta I e II.
-
- Separando H(z) em dois blocos , e obtendo o sinal intermediário W(z) ou Y(z) dependendo da ordem dos blocos.
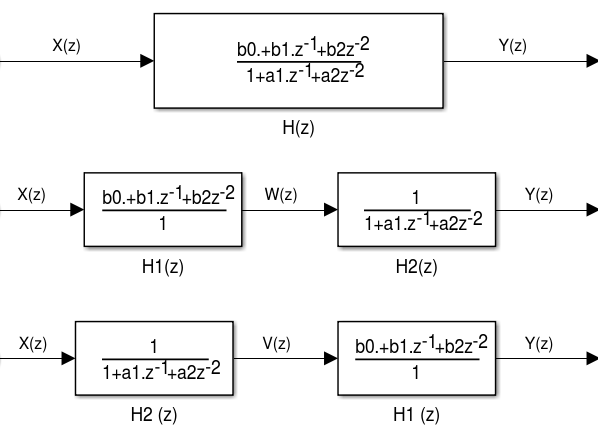
- Com o ordenamento dos blocos e em ordem direta teremos a Forma Direta I:
- Podemos obter a realização de na forma direta.
- Para obter a realização de , é necessário reescrever a saída em função de e das saídas anteriores e :
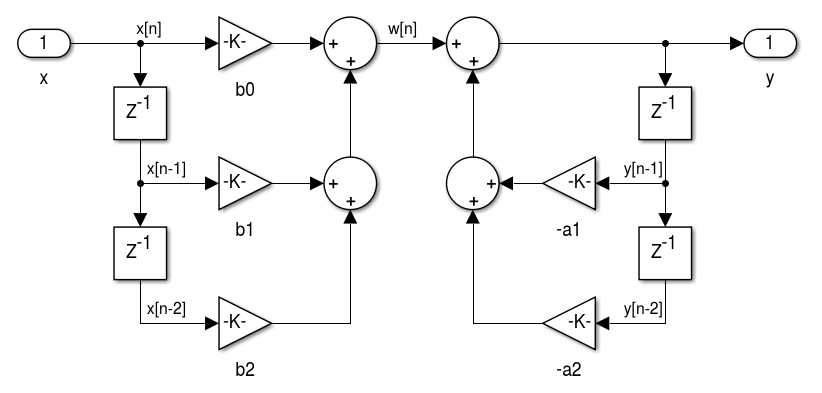
- Com o ordenamento dos blocos e em ordem reversa teremos a Forma Direta II:
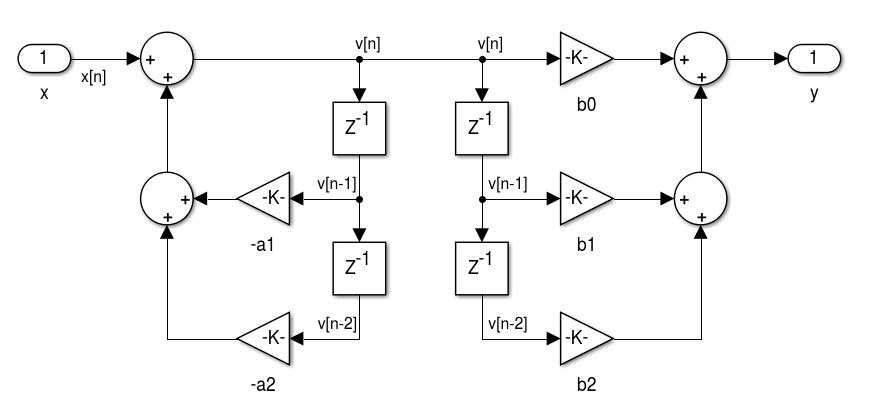
- Considerando que os sinais no centro são idênticos podemos simplificar e obter a Forma Direta II (Canônica):
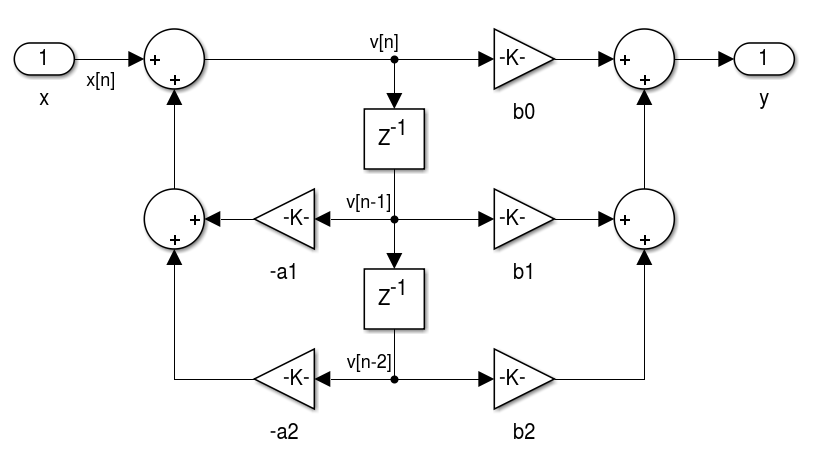
- Considerando as regras de transposição podemos obter a forma transposta I e II. A transposição consiste na inversão do fluxo de todos os sinais, substituição de nós de soma por derivações e as derivações por soma. A entrada e saída também devem ser invertidas. A realização da transposição não altera o sistema implementado.
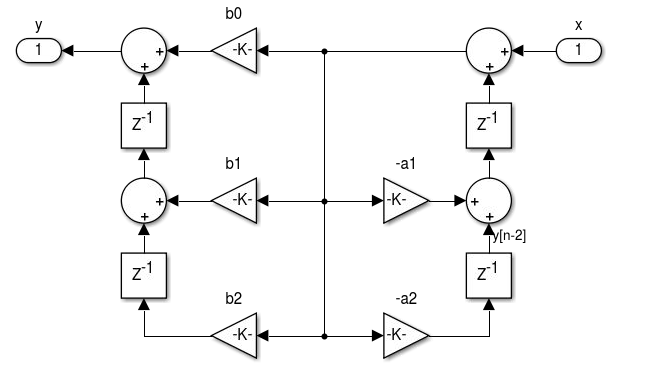
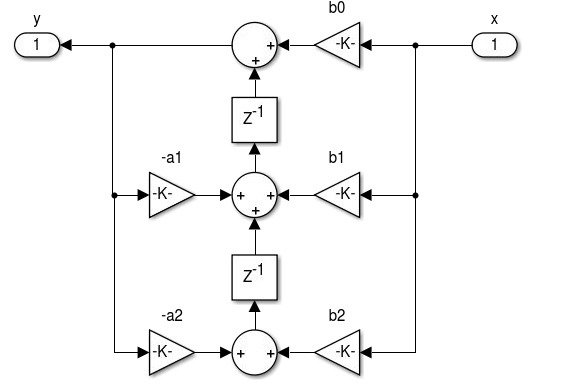
- Realização de filtros IIR de ordem maior que 2: Forma Direta I e II, Transposta I e II, Cascata, Paralela
- Os filtros IIR de ordem superior a 2 podem ser implementados nas FD I ou II e na FT I ou II. No entanto nessa configuração tendem a ficar instáveis ao terem os coeficientes quantizados, e também terem uma significativa alteração da resposta em frequência. Para reduzir esses problemas uma possível solução é a decomposição em filtros de 2ª ordem para serem associados na forma em Cascata ou Paralela.
- Filtros Digitais: Ferramentas do Matlab para projeto
- Practical Introduction to Digital Filter Design
- Filter Design Gallery
- Função para projeto de filtros - designfilt
- Aula 23 ()
- Filtros Digitais: Utilização de filtros FIR
- Utilizar o Audacity para gerar sinais de teste. Gere os seguintes sinais e analise seus espectrogramas:
- Um sinal DTMF com duração de 1 segundo com frequência de amostragem de 8 kHz, correspondente aos dígitos 1234567890 ('Dtmf.wav').
- Um sinal contendo ruído branco com duração de 5 segundo com frequência de amostragem de 8 kHz ('RuidoBranco.wav').
- Um sinal onda quadra com duração de 2 segundo com frequência de amostragem de 8 kHz e período de 2 ms ('Quadrada.wav').
Utilize o Matlab para gerar o seguinte sinal:
- Um sinal de varredura de Cosseno entre 0 Hz e 4 kHz com duração de 1 segundo.
Fs = 8000;
t = 0:1/Fs:1-1/Fs;
x = chirp(t,0,1,4000);
spectrogram(x, blackman(128), 120, 200, Fs,'yaxis')
audiowrite('Chirp0-4kHz.wav',x,Fs)
sound(x,Fs) % Atenção remova o fone de ouvido antes de realizar este procedimento.
Utilizar o Matlab para projetar os seguintes filtros FIR e transmitir os sinais obtidos acima. Em todos os filtros considere a frequência de amostragem como 8 kHz, atenuação máxima na banda de passagem de 0,5 dB, e as bandas de transição como 400 Hz. Use a janela de Kaiser.
- Filtro passa-baixas com fc = 1,5 kHz e atenuação de 60 dB na rejeição;
- Filtro passa-altas com fc = 2,5 kHz e atenuação de 30 dB na rejeição;
- Filtro passa faixa com fc1 = 1,5 kHz e fc2 = 2,5 kHz e atenuação de 80 dB na rejeição;
- Filtro rejeita faixa com fc1 = 1,9 kHz e fc2 = 2,1 kHz e atenuação de 80 dB na rejeição;
Após obter os filtros, transmita cada um dos sinais gerados no Audacity através do filtro e verifique o resultado obtido analisando os sinal obtidos comparando o espectrograma com a resposta em magnitude do filtro.
[x, Fs] = audioread('Chirp0-4kHz.wav'); % Leitura do sinal
t = (0:length(x)-1)/Fs; % Vetor de tempo
b = fir1(48,[2000 2100]/Fs); % Filtro Hamming com ordem 48 passa faixa
sound(x,Fs) % Atenção remova o fone de ouvido antes de realizar este procedimento.
y = filter(b,1,x);
sound(y,Fs) % Atenção remova o fone de ouvido antes de realizar este procedimento.
subplot(311); spectrogram(x, blackman(128), 100, 200, Fs)
subplot(312); spectrogram(y, blackman(128), 100, 200, Fs)
[Hw, w] = freqz(b,1,2000);
subplot(313); plot(w/pi*Fs/2,20*log10(abs(Hw))); ylim([-100,0]);
- Ver as funções audioread, audiowrite, chirp, spectrogram, filter do Matlab.
- Aula 24 e 25(31 Out e 3 Nov)
- Projeto de um receptor DTMF.
- cada aluno deverá projetar dois discriminadores de frequências correspondente a duas linhas e duas colunas do sistema DTMF.
- As especificações do discriminador de frequência, mostrado na figura, são:
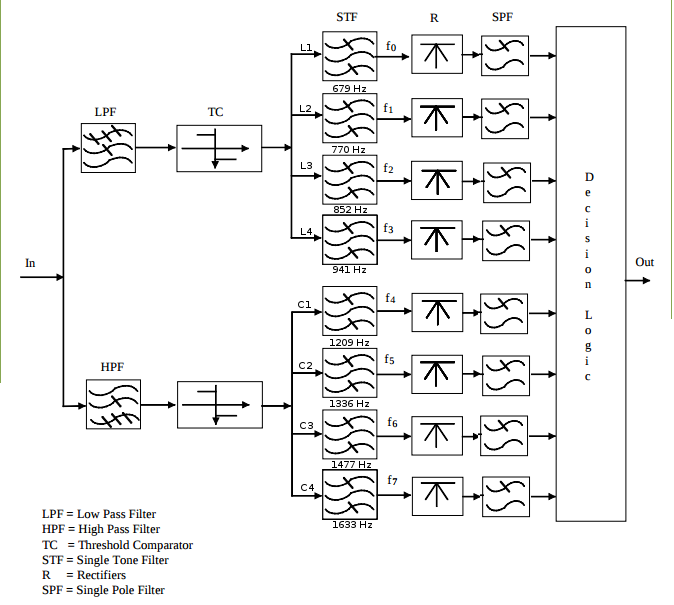
- A frequência de amostragem f_s do sinal de entrada é de 8 kHz.
- Os filtros passa banda (BP) deverão ter, inicialmente, uma largura de banda BW' correspondente a 10% da frequência central f_0.
- Os filtros passa baixa (LP) deverão ter, inicialmente, uma freqüência de passagem f_p de 100 Hz.
- O circuito retificador deve se implementado pela função abs.
- Neste projeto o sinal de entrada terá uma frequência de amostragem do sinal de de 44.100 Hz. Recomenda-se que antes de realizar todas as filtragens indicadas no diagrama, se faça uma filtragem passa-baixa com um filtro de 2 polos do tipo Butterworth ou Chebychev 1, com fc = 0.5*44.100/11 ~ 2kHz, seguido de uma subamostragem para a nova frequência de ~ 4kHz.
Ver as especificações DTMF em:
- ETSI ES 201 235-1 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 1: General
- ETSI ES 201 235-2 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 2: Transmitters
- ETSI ES 201 235-3 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 3: Receivers
- ETSI ES 201 235-4 - Specification of Dual Tone Multi-Frequency (DTMF) Transmitters and Receivers; Part 4: Receivers for use in Terminal Equipment for end-to-end signalling
- Aula 26 ()
- Atraso de grupo em filtros IIR e FIR no Matlab}}
- O atraso de grupo de um filtro é a medida da atraso médio do filtro em função da frequência do sinal de entrada. Ele é obtido pela primeira derivada da resposta de fase do filtro. Se a resposta em frequencia é , então o atraso de grupo é:
- onde é a fase de .
- Um filtro sem distorção de fase (Não causal) pode ser obtido ao passar uma sequencia x(n) por um filtro H1, tomando a saída do filtro revertida e passando novamente pelo mesmo filtro H1. A saída do último filtro revertida corresponde ao sinal x(n) filtro com fase zero. O filtro obtido desta forma tem as seguintes características:
- A Distorção de fase nula
- A função de transferência do filtro é igual a magnitude ao quadrada da função de transferência original do filtro H1.
- A ordem do filtro é o dobro da ordem do filtro H1.
- Exemplo de aplicação a filtragem de um sinal ECG com ruído Arquivo:Noisyecg.txt noisyecg.mat:
%% Carregando um sinal de ECG com ruído com duração de 4 segundos.
load noisyecg.mat
x = noisyECG_withTrend;
fa = 500; %% 2000 amostras em 4 segundos => 500 amostras por segundo.
t = [0:length(x)-1]*1/fa;
plot(t,x);
%% Projetando um filtro passa-baixa tipo IIR butter com f_passagem = 0.15 rad/s
d = designfilt('lowpassiir', ...
'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
'PassbandRipple',1,'StopbandAttenuation',60, ...
'DesignMethod','butter');
freqz(d)
%% Filtro de x revertido x e somando com x filtrado. OFF LINE
y = flip(filter(d,flip(filter(d,x))));
y1 = filter(d,x);
figure(2);
subplot(2,1,1)
plot(t, [y y1])
title('Filtered Waveforms')
legend('Zero-phase Filtering','Conventional Filtering')
subplot(2,1,2)
plot(t, [x y])
title('Original Waveform')
legend('noisy ecg ','fitered ecg')
- Verifique também o resultado da filtragem usando um filtro IIR (ellip, cheby1 ou cheby2) e filtros FIR (equiripple e de janela)
%% Projetando um filtro passa-baixa tipo FIR equiripple com f_passagem = 0.15 rad/s
d = designfilt('lowpassfir', ...
'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
'PassbandRipple',1,'StopbandAttenuation',60, ...
'DesignMethod','equiripple');
y = flip(filter(d,flip(filter(d,x))));
- Note que nos filtros FIR de fase linear o procedimento mais simples é adiantar o sinal de acordo com o atraso de grupo (metade da ordem do filtro), devendo-se tomar cuidado para arredondar a meia amostra nos filtros de ordem impar.
y1 = filter(d,x);
gd = grpdelay(d);
gd1 = ceil(gd(1));
y = [y1(gd1:end); zeros(gd1-1, 1)];
O cálculo do atraso de grupo pode ser realizado utilizando a função grpdelay ou diretamente pela definição da derivada do ângulo em relação a frequência:
%% Calculo do atraso de grupo
% Método 1 - uso da função grpdelay
[z,p,k] = butter(30,0.2);
sos = zp2sos(z,p,k);
[gd,w]=grpdelay(sos,128);
figure(1)
plot(w/pi,gd),grid on;
% Método 2 - derivada obtida por aproximação discreta
% calculo a cada par de pontos (w2-w1)/delta_w
[h,w] = freqz(sos);
a = unwrap(angle(h));
hold on; plot(w/pi,a,'g');
delta_w = pi/length(a);
plot(w(1:end-1)/pi+delta_w/2,-(a(2:end)-a(1:end-1))/delta_w,'r');
- Ler Gustafsson, F. "Determining the initial states in forward-backward filtering." IEEE® Transactions on Signal Processing. Vol. 44, April 1996, pp. 988–992, artigo que propos um técnica de minimizaçao dos transientes de inicio e fim do sistema linear.
1.5 Unidade 5
- Aula 27 a 29 ()
-
- Uso do Simulink
- Uso dos blocos de simulação sinewave, scope e Spectrum Analyzer.
- Outros blocos mux, demux, sum, product.
- Exemplo: construção de um modulador AM.
- Interactive Simulink Tutorial
-
- Introduction: What Is Simulink? 4:42
- Constructing and Running a Simple Model 13:45
- Simulating a Model 10:10
-
- Bases da modelagem gráfica com Simulink (45 minutos)
- Working with MATLAB 9:12 - Pass data between Simulink and MATLAB
- Creating Subsystems 6:46 - Simplify your model by grouping blocks into subsystems
- É importante ler informações complementares sobre o Solver Pane, Model Simulation, Choose a Solver
-
- Usando o Simulink para modelagem de Sistemas Dinâmicos Discretos(60 minutos)
- Modeling Discrete Dynamical Systems 19:35 - Learn to use the Integer Delay and Discrete Filter blocks to model difference equations
- Use DSP System Toolbox 12:01 - Explore the basics of DSP System Toolbox, and model a simple system
- Working with Signals in Simulink 9:59 - Learn frame-based processing and its benefits, and visualize signals in frequency domain
- Applying a Filter 9:04 - Learn to model noise and implement a hand-designed filter to remove noise
- Designing and Implementing a Filter 10:23 - Design a digital filter using the filter design tool and review signal processing application examples
- dspstartup.m command
- É importante ler informações complementares sobre, Tempo de amostragem (Time Sample), View Sample Time Information, Sample- and Frame-Based Concepts, Vector Concatenate, Matrix Concatenate.
- Aula 30 e 31
- Projeto do Detector de DTMF utilizando o Simulink.
1.6 ATUAL
- Aula 32 a 34
-
- Uso do HDL Coder
- Getting Started with MATLAB to HDL Workflow
- Basic HDL Code Generation with the Workflow Advisor
- Floating-Point to Fixed-Point Conversion
- Verify HDL Model with MATLAB Testbench
- Ver também o uso da função fi - Construct fixed-point numeric object
a = fi(-1, true, 8, 0) a.bin
a = fi(-128, true, 8, 0) a.bin
a = fi(127, true, 8, 0) a.bin
- Ver também a função resize da ieee.numeric_std library.
function RESIZE (ARG: SIGNED; NEW_SIZE: NATURAL) return SIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with the sign bit (ARG'LEFT). When truncating,
-- the sign bit is retained along with the rightmost part.
function RESIZE (ARG: UNSIGNED; NEW_SIZE: NATURAL) return UNSIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with '0'. When truncating, the leftmost bits
-- are dropped.
- Simulação do projeto no ModelSim-ALTERA.
| Procedimentos para a Simulação |
|---|
|
Abra o ModelSim: /opt/altera/13.0sp1/modelsim_ase/bin/vsim & Troque a pasta de trabalho para a pasta onde o Matlab gerou os arquivos .vhd e .do [File > Change Directory] ou digite na janela tcl: cd /tmp/mlhdlc_sfir/codegen/mlhdlc_sfir/hdlsrc Execute o arquivo do mlhdlc_sfir_fixpt_tb_compile.do NOTA: Se você selecionou [x] Simulate generated HDL test bench durante o Workflow, edite o arquivo mlhdlc_sfir_fixpt_tb_sim.do, comentando as linhas que forçam a saida do Modelsim. Estas linhas foram criadas para a integração direta com o Matlab, mas ela não funciona com a versão do ModelSim que temos disponível. edit mlhdlc_sfir_fixpt_tb_sim.do #onerror {quit -f}
#onbreak {quit -f}
...
#quit -f
Agora execute o arquivo mlhdlc_sfir_fixpt_tb_sim.do, o qual irá adicionar os sinais a serem analisados na janela Wave e executará todos os comandos vhdl do arquivo *_tb.vhdl gerado pelo Matlab. do mlhdlc_sfir_fixpt_tb_sim.do Ao tinal da simulação a janela Transcript indicará se o teste passou: # ** Note: **************TEST COMPLETED (PASSED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb ou se falhou: # ** Note: **************TEST COMPLETED (FAILED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb Note ainda que os sinais de entrada (x_in), os sinais de saída (y_out e delayed_xout) e os dois sinais de referência gerados na simulação com o Matlab (y_out_ref e delayed_xout_ref) são mostrados como sequências de bits. Para melhorar a visualização mude o Formato desses sinais para analógico [Clique Direito do Mouse> Format > Analog (automatic)]. |
- Implementar o filtro indicado abaixo e realizar a simulação com MODELSIM
| Exemplo de um Filtro IIR |
|---|
% FILE mlhdlc_iir_filter.m
function y = mlhdlc_iir_filter(x, sos, g)
% Declare persistent variables and initialize
numSections = numel(sos)/6;
persistent z
if isempty(z)
z = zeros(numSections, 2);
end
y = x;
for k=coder.unroll(1:numSections)
curSOS = sos((k-1)*6+1:k*6);
[y z(k,:)] = biquad_filter(y, curSOS(1:3), curSOS(4:6), z(k, :));
end
y = y * g;
end
function [y, z] = biquad_filter (x, b, a, z)
% a(1) is assumed to be 1
% Direct-form II implementation
tmp = x - z(1)*a(2) - z(2)*a(3);
y = z(2) * b(3) + z(1) * b(2) + tmp * b(1);
z(2) = z(1);
z(1) = tmp;
end
% Copyright 2011-2013 The MathWorks, Inc.
% FILE: mlhdlc_iir_filter_tb.m
clear mlhdlc_iir_filter;
% All frequency values are in MHz.
Fs = 100; % Sampling Frequency
N = 4; % Order
Fc1 = 29.5; % First Cutoff Frequency
Fc2 = 30.5; % Second Cutoff Frequency
[z,p,k] = butter(N/2,[Fc1 Fc2]/(Fs/2),'bandpass');
[sos1,g1] = zp2sos(z,p,k); % Convert to SOS form
[num,den] = zp2tf(z,p,k);
L = 1000;
Fs = Fs*1e6 % Passa para MHz
t = (0:L-1)'/Fs;
x = 0.5*sin(2*pi*30e6*t) + 0.5*cos(2*pi*20e6*t) + + 0.5*cos(2*pi*35e6*t);
rng('default'); % always default to known state
x = x + .5*randn(size(x)); % noisy signal
y = zeros(size(x));
%%
% Call to the design
sos = sos1.';
g = g1;
for k=1:numel(x)
y(k) = mlhdlc_iir_filter(x(k), sos(:), g);
end
%%
close all;
figure('Name', [mfilename, '_psd_plot']);
pwelch(x, 128);
hold on;
pwelch(y, 128);
yh = get(gca,'Children');
set(yh(1),'Color','r');
|
- Ver também
2 Avaliações
- Entrega dos diversos trabalhos ao longo do semestre.
- Projeto Final. O projeto é avaliado nos quesitos: 1) Implementação do Sistema, 2) Documentação, 3) Avaliação Global do aluno no projeto.
2.1 Atividades extra
Neste tópico serão listadas as atividades extras que os alunos da disciplina deverão realizar ao longo do curso.
| AE1 - Variação do Experimento 1.2 (prazo XX/Ago/2016) |
|---|
|
No Experimento 1.2 varie o valor da frequência de amostragem de 6 até 20 Hz e observe:
|
| AE1 - Projeto de Filtros Digitais IIR (Prazo de entrega 10/10/2016 as 02:10:10 (madrugada)) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| AE2 - Projeto de Filtro Digitais FIR - MATLAB (Prazo de entrega 21/10/2016) |
|---|
|
| AE3 - Projeto de Detectores DTMF - MATLAB (Prazo de entrega 22/11/2016) |
|---|
|
| AE4 - Projeto de Detectores DTMF - SIMULINK (Prazo de entrega 04/12/2016) |
|---|
|
| AE5 - Projeto de Detectores DTMF - VHDL (Prazo de entrega 19/12/2016) |
|---|
|
3 Referências Bibliográficas
- ↑ 1,0 1,1 1,2 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822
- ↑ LATHI, Bhagwandas P. Sinais e Sistemas Lineares. 2. ed. Porto Alegre: Artmed-Bookman, 2007. 856 p. ISBN 978-8560031139