PSD29007-Engtelecom(2015-2) - Prof. Marcos Moecke
1 Registro on-line das aulas
1.1 Unidade 1
- Aula 1 (29 Jul)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Resposta de sistemas LTI (Experimento 1.1)
- Relembrar o conceito de equação de diferenças de um sistema LTI discreto e resposta ao impulso.
- Resposta ao delta de Kronecker do sistema LTI discreto
- onde , e logo
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.1
alpha = 1.15; N = 256;
x = [1 zeros(1,N)];
y = filter(1,[1 -1/alpha],x);
stem(y);
- Amostragem de Sinais (Experimento 1.2)
- Relembrar teorema da amostragem. Efeito da amostragem abaixo da frequência de Nyquist. Aliasing.
- Notar que as amostras de um sinal (3 Hz) e um sinal (7 Hz) são idênticas quando amostrado com um sinal de 10 Hz.
% Exemplos e Experimentos baseados no livro:
% DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235.
%% Experimento 1.2
fs = 10; % frequencia (Hz) de amostragem dos sinais
Ts = 1/fs; fase = 0;
time = 0:Ts:(1-Ts);
f1 = 3; % frequencia (Hz) do sinal s_1
f2 = 7; % frequencia (Hz) do sinal s_2
s_1 = cos(2*pi*f1*time+fase);
s_2 = cos(2*pi*f2*time+fase);
fsa = 1000; % frequência auxiliar de amostragem usada apenas para representação dos sinais originais
Tsa = 1/fsa;
time_aux = 0:Tsa:(1-Tsa);
figure(1);
stem(time,s_1,'ob');
hold on;
plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k');
stem(time,s_2,'+r');
plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m');
hold off;
legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo')
- Uso do Matlab: Help, F9 executa o código destacado no Help. Programação com scripts .m, Execução de seções e variação de valores nos scripts,
- Ver no Matlab: zeros, ones, plot, stem, subplot, filter.
- Uso de gráficos no Matlab.
- Ver pag. 65 a 71 de [1]
- Ver também PDF Documentation for MATLAB. Principalmente MATLAB Primer.
- Suspensão do calendário acadêmico pela direção do Campus de 30 de Julho a 1 de Outubro;
- Aula 2-3 (2-7 Out)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
| Variação do Experimento 2.2 |
|---|
%% Experimento 2.2
% Resposta em frequencia usando a função freqz
N = 1;
num = [1 0 0 0];
den = poly([0.8 0.2])
%den = [1 0.6 -0.16];
% modo 1
%[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]);
%plot(w/pi, abs(H));
% modo 2
%[H,w]=freqz(num,den);
%plot(w/pi, abs(H));
% modo 3
%[H,w]=freqz(num, den, 'whole');
%plot(w/pi, abs(H));
% modo 4
freqz(num, den, 'whole');
figure(2);
zplane(num,den);
%% Resposta em frequencia substituindo z -> e^(jw)
syms z
Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z);
pretty(Hf)
latex(Hf)
N = 1;
w = [0:pi/100:N*pi-pi/100];
plot(w/pi,abs(Hf(exp(1i*w))))
%title(['$' latex(Hf) '$'],'interpreter','latex')
text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex')
xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex')
|
- Aula 3 (9 Out)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Filtros Digitais (Experimento 2.3)
- Filtragem de Sinais (Experimento 3.1)
- Aula 4 (14 Out)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab
- Análise de Sinais (Experimento 3.2)
- Análise de um sistema h[n] correspondente a um filtro passa-faixa, utilizando um sinal de entrada x[n] senoidal (ou um sinal r[n] de ruído branco). Análise da entrada x[n] e saída y[n] usando a fft.
1.2 Unidade 2
- Aula 5 (16 Out)
- Filtros Digitais: Filtros IIR:
- Aproximação de magnitude de filtros analógicos: do tipo Butterworth.
- Ver pag. 186 a 194 de [2]
- Aula 6 (21 Out)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros analógicos passa-baixas: do tipo Butterworth. (continuação)
- Ver pag. 194 a 204 de [2]
- Aula 7 (23 fev)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros analógicos passa-baixas: do tipo Butterworth. (continuação)
- Projeto de filtros analógicos passa-baixas: do tipo Chebyshev I.
- Ver pag. 204 a 208 de [2]
- Aula (13 Nov)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros digitais IIR com Matlab. Uso das funções buttord, butter, cheb1ord, cheby1, cheb2ord, cheby2, ellipord, ellip.
- Uso do MatLab na analise da resposta em frequência de filtros digitais. Uso das funçoes freqz, grpdelay, zplane, filter, fvtool.
- Projetar um filtro com duas bandas de passagem, onde: Ap = 0.1; Ar = 60; características da 1ª banda de passagem (wr1 = 0.15, wp1 = 0.2, wp2 = 0.3, wr2 = 0.35); características da 1ª banda de passagem (wr1 = 0.45, wp1 = 0.5, wp2 = 0.6, wr2 = 0.65).
- DICA: Para multiplicar dois polinômios pode ser utilizado a convolução.
- Aula 7 (3 mar)
- Filtros Digitais: Filtros IIR:
- Transformação de frequência de filtros analógicos
- (passa-baixas -> passa-baixas, passa-baixas -> passa-altas, passa-baixas -> passa-faixa, passa-baixas -> rejeita-faixa)
- Uso das funções semilogx, semilogy,logspace, linspace.
- Ver em IIR Filter Design,
- Funçãos para projeto do filtro final (analógico com 's'): besself, butter, cheby1, cheby2, ellip
- Funções de estimação da ordem do filtro: buttord, cheb1ord, cheb2ord, ellipord
- Funções para projeto do filtro protótipo analógico passa-baixas: besselap, buttap, cheb1ap, cheb2ap, ellipap
- Funções de transformação de frequencia: lp2bp, lp2bs, lp2hp, lp2lp
- Ver pag. 208 a 218 de [2]
- Aula 8 (6 mar)
- Filtros Digitais: Filtros IIR: transformações do tempo contínuo no tempo discreto
- Transformação invariante ao impulso (apenas para filtros com forte atenuação em frequência altas, ex: passa-baixas e passa-faixa)
- Transformação bilinear (para todos tipos de filtro)
- Ver em IIR Filter Design,
- Filter discretization functions: bilinear, impinvar
1.3 Unidade 3
- Aula 9 (10/mar)
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: simétricos e antisimétricos
- Ver pag. 249 a 256de [2]
- Aula 10 (13/mar)
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: propriedades
- Ver pag. 256 a 260 de [2]
- Aula XX (27/nov)
- Filtros Digitais: Filtros FIR
- Coeficientes da série de Fourier de filtros ideias: LP, HP, BP, BS
- Passa-baixas (Low-pass)
- Passa-altas (High-pass)
- Passa-faixa (Band-pass)
- Rejeita-banda (Band-stop)
- Janela retangular, fenômeno de Gibbs
- Uso de funções de janelamento temporal no projeto de filtros digitais.
- Tipos de janelas temporais usadas no projeto de filtros digitais.
- Retangular
- Bartlett
- Hanning
- Hamming
- Blackman
- em todas as janelas quando
- Aula XX (2/dez)
- Filtros Digitais: Filtros FIR
- Projeto de filtro FIR utilizando janelas temporais
- Uso de janelas fixas no Matlab : rect, triang, bartlett, hann, hamming, blackman, blackmanharris, nuttall.
L = 64;
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));
| Janela | |||
|---|---|---|---|
| Retangular | 13.3 | {{{4}}} | |
| Triangular | 26.6 | {{{4}}} | |
| Barlett | 26.5 | {{{4}}} | |
| Hann | 31.5 | {{{4}}} | |
| Barlett-Hanning | 35.9 | {{{4}}} | |
| Hamming | 42.5 | {{{4}}} | |
| Bohman | 46.0 | {{{4}}} | |
| Parzen | 53.1 | {{{4}}} | |
| Backman | 58.1 | {{{4}}} | |
| Flat Top | 88.0 | {{{4}}} | |
| Backman-Harris | 92.1 | {{{4}}} | |
| Nutfall | 93.8 | {{{4}}} |
- Dados acima obtidos para um filtro passa baixas de ordem N = 64 com
L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
Para a janela de Kaiser, a estimação do fator e da ordem do filtro são obtidos por:
- onde é a atenuação do lóbulo lateral e é a largura da banda de transição em rad/amostra.
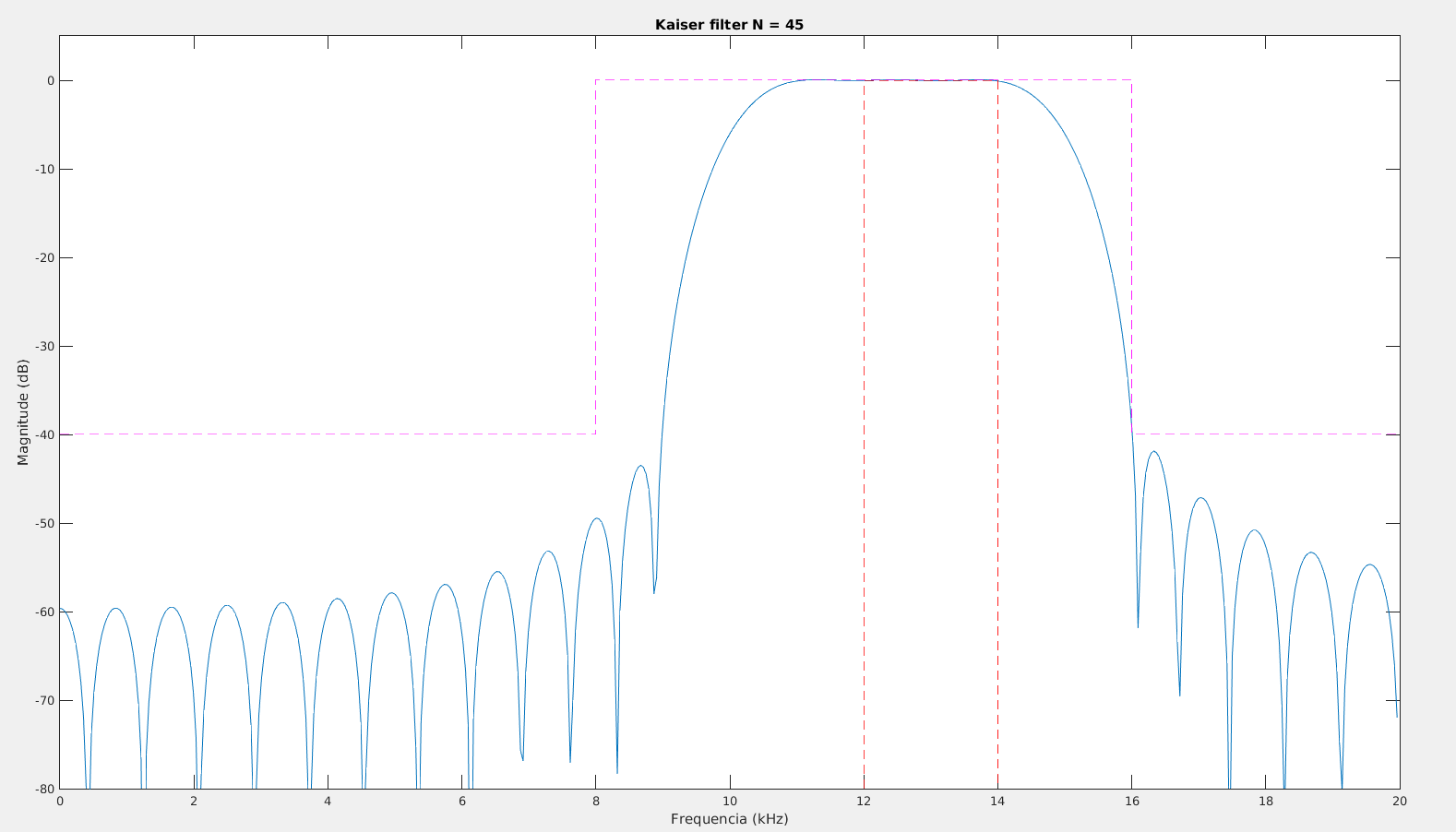
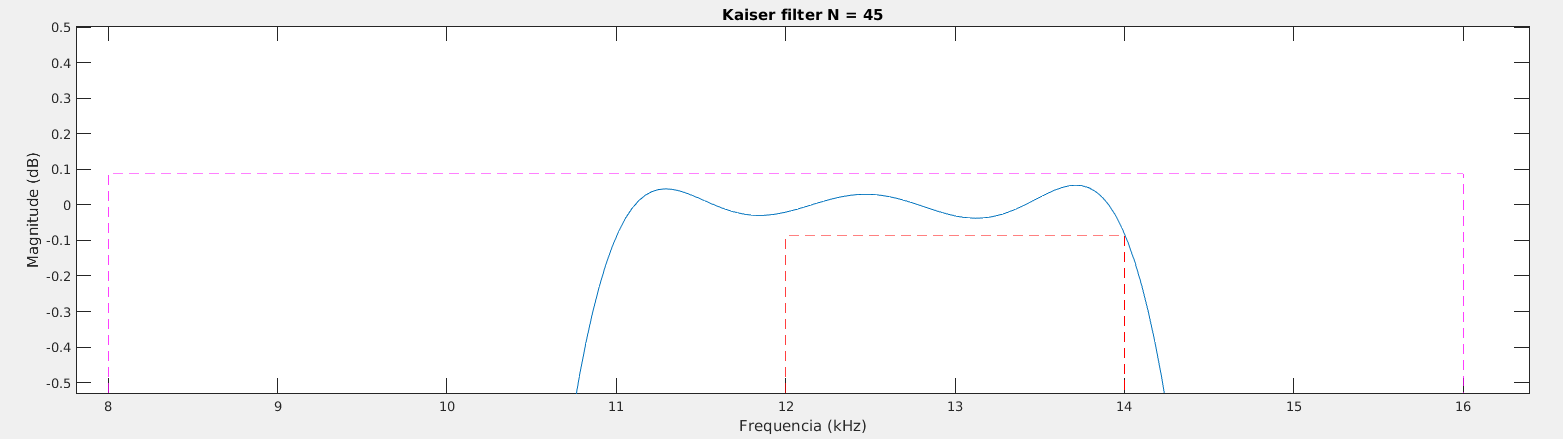
Utilizando o Matlab é possível estimar esses valores utilizando a função kaiserord. Exemplo da obtenção de um filtro passa baixa com , , atenuação de 40 dB na "stopband"
fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.01 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
Com os parâmetros é possível projetar o filtro usando a função fir1, que utiliza o método da janela para o projeto do filtro.
h_fir = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[Hw,w] =freqz(h_fir);
plot(w*fsamp/2/pi,20*log10(abs(Hw)))
title(['Kaiser filter N = ' num2str(n)])
%fvtool(h_fir,1)
1.4 ATUAL
- Aula XX (9/dez)
- Filtros Digitais: Filtros FIR
Utilizar o Audacity para gerar sinais de teste. Gere os seguintes sinais e analise seus espectrogramas:
- Um sinal DTMF com duração de 1 segundo com frequência de amostragem de 8 kHz, correspondente aos dígitos 1234567890 ('Dtmf.wav').
- Um sinal contendo ruído branco com duração de 5 segundo com frequência de amostragem de 8 kHz ('RuidoBranco.wav').
- Um sinal onda quadra com duração de 2 segundo com frequência de amostragem de 8 kHz e período de 2 ms ('Quadrada.wav').
Utilize o Matlab para gerar os seguintes sinais:
- Um sinal de varredura de Cosseno entre 0 Hz e 4 kHz com duração de 1 segundo.
Fs = 8000;
t = 0:1/Fs:1-1/Fs;
x = chirp(t,0,1,4000);
spectrogram(x, blackman(128), 120, 200, Fs,'yaxis')
audiowrite('Chirp0-4kHz.wav',x,Fs)
sound(x,Fs) % Atenção remova o fone de ouvido antes de realizar este procedimento.
Utilizar o Matlab para projetar os seguintes filtros FIR e transmitir os sinais obtidos acima. Em todos os filtros considere a frequência de amostragem como 8 kHz, atenuação máxima na banda de passagem de 0,5 dB, e as bandas de transição como 400 Hz. Use a janela de Kaiser.
- Filtro passa-baixas com fc = 1,5 kHz e atenuação de 60 dB na rejeição;
- Filtro passa-altas com fc = 2,5 kHz e atenuação de 30 dB na rejeição;
- Filtro passa faixa com fc1 = 1,5 kHz e fc2 = 2,5 kHz e atenuação de 80 dB na rejeição;
- Filtro rejeita faixa com fc1 = 1,9 kHz e fc2 = 2,1 kHz e atenuação de 80 dB na rejeição;
Após obter os filtros, transmita cada um dos sinais gerados no Audacity e verifique o resultado obtido analisando os sinal obtidos comparando o espectrograma com a resposta em magnitude do filtro.
[x, Fs] = audioread('Chirp0-4kHz.wav'); % Leitura do sinal
t = (0:length(x)-1)/Fs; % Vetor de tempo
b = fir1(200,[2000 2100]/Fs); % Filtro Hamming com ordem 48 passa faixa
[Hw, w] = freqz(b,1,2000);
y = filter(b,1,x);
subplot(311); spectrogram(x, blackman(128), 100, 200, Fs)
subplot(312); plot(w/pi*Fs,20*log10(abs(Hw))); colorbar; ylim([-100,0]);
subplot(313); spectrogram(y, blackman(128), 100, 200, Fs)
- Ver as funções audioread, audiowrite, chirp, spectrogram, filter do Matlab.
- Ver pag. 266 a 273 de [2]
1.5 Unidade 5
- Aula
-
- Uso do Simulink
- Aula
-
- Uso do Simulink
-
-
- Introduction: What Is Simulink? 4:42
- Constructing and Running a Simple Model 13:45
- Simulating a Model 10:10
- Working with MATLAB 9:12
- Creating Subsystems 6:46
- É importante ler informações complementares sobre o Solver Pane, Model Simulation, Choose a Solver
-
- Aula
-
- Uso do Simulink
-
-
- Modeling Discrete Dynamical Systems 19:35
- Use Signal Processing Blockset 12:01
- dspstartup.m command
- Working with Signals in Simulink 9:59
- É importante ler informações complementares sobre, Tempo de amostragem (Time Sample), View Sample Time Information, Sample- and Frame-Based Concepts, Vector Concatenate, Matrix Concatenate
-
- Aula
-
- Uso do HDL Coder
- Getting Started with MATLAB to HDL Workflow
- Basic HDL Code Generation with the Workflow Advisor
- Floating-Point to Fixed-Point Conversion
- Verify HDL Model with MATLAB Testbench
- Ver também o uso da função fi - Construct fixed-point numeric object
a = fi(-1, true, 8, 0) a.bin
a = fi(-128, true, 8, 0) a.bin
a = fi(127, true, 8, 0) a.bin
- Ver também a função resize da ieee.numeric_std library.
function RESIZE (ARG: SIGNED; NEW_SIZE: NATURAL) return SIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with the sign bit (ARG'LEFT). When truncating,
-- the sign bit is retained along with the rightmost part.
function RESIZE (ARG: UNSIGNED; NEW_SIZE: NATURAL) return UNSIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with '0'. When truncating, the leftmost bits
-- are dropped.
- Aula
-
- Uso do HDL Coder
- Simulação do projeto da aula anterior no ModelSim-ALTERA.
| Procedimentos para a Simulação |
|---|
|
Abra o ModelSim: /opt/altera/13.0sp1/modelsim_ase/bin/vsim & Troque a pasta de trabalho para a pasta onde o Matlab gerou os arquivos .vhd e .do [File > Change Directory] ou digite na janela tcl: cd /tmp/mlhdlc_sfir/codegen/mlhdlc_sfir/hdlsrc Execute o arquivo do mlhdlc_sfir_fixpt_tb_compile.do Edite o arquivo mlhdlc_sfir_fixpt_tb_sim.do, comentando as linhas que forçam a saida do Modelsim. Estas linhas foram criadas para a integração direta com o Matlab, mas ela não funciona com a versão do ModelSim que temos disponível. edit mlhdlc_sfir_fixpt_tb_sim.do #onerror {quit -f}
#onbreak {quit -f}
...
#quit -f
Agora execute o arquivo mlhdlc_sfir_fixpt_tb_sim.do, o qual irá adicionar os sinais a serem analisados na janela Wave e executará todos os comandos vhdl do arquivo *_tb.vhdl gerado pelo Matlab. do mlhdlc_sfir_fixpt_tb_sim.do Ao tinal da simulação a janela Transcript indicará se o teste passou: # ** Note: **************TEST COMPLETED (PASSED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb ou se falhou: # ** Note: **************TEST COMPLETED (FAILED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb Note ainda que os sinais de entrada (x_in), os sinais de saída (y_out e delayed_xout) e os dois sinais de referência gerados na simulação com o Matlab (y_out_ref e delayed_xout_ref) são mostrados como sequências de bits. Para melhorar a visualização mude o Formato desses sinais para analógico [Clique Direito do Mouse> Format > Analog (automatic)]. |
| Problemas na integração Matlab - Modelsim |
|---|
sudo gedit quartus
|
2 Avaliações
- Entrega dos diversos trabalhos ao longo do semestre.
- Projeto Final. O projeto é avaliado nos quesitos: 1) Implementação do Sistema, 2) Documentação, 3) Avaliação Global do aluno no projeto.
2.1 Atividades extra
Neste tópico serão listadas as atividades extras que os alunos da disciplina deverão realizar ao longo do curso. É importante observar o prazo de entrega, pois os conceitos serão reduzidos conforme o atraso na entrega. Para a entrega no prazo os conceitos possíveis são (A, B, C, D). Entrega com até uma semana de atraso (B, C, D). Entrega com até duas semanas de atraso (C ou D). Entrega com mais de duas semanas de atraso (D).
2.1.1 PARA ENTREGAR
| AE6 - Projeto de Filtro Digitais FIR x IIR (Prazo de entrega XX/XX/2016) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.1.2 JÁ ENCERRADAS
| AE1 - Experimento 3.2 (Prazo de entrega 23/10/2015) |
|---|
|
| AE2 - Projeto de Filtro Analógico Butterworth (Prazo de entrega 04/11/2015) |
|---|
|
| AE3 - Projeto de Filtro Analógicos LP, HP, BP, BS (Prazo de entrega 27/11/2015) | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| AE4 - Estudo dos 4 tipos de filtros FIR com fase linear (Prazo de entrega 04/12/2015) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| AE5 - Estudo dos filtros FIR tipo Janela (Prazo de entrega XX/12/2015) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.1.3 ESTUDOS SEM ENTREGA DE DOCUMENTAÇÃO
| AL1 - Variação do Experimento 1.2 |
|---|
|
No Experimento 1.2 varie o valor da frequência de amostragem de 6 até 20 Hz e observe:
|
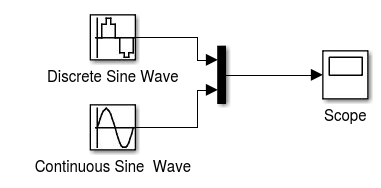
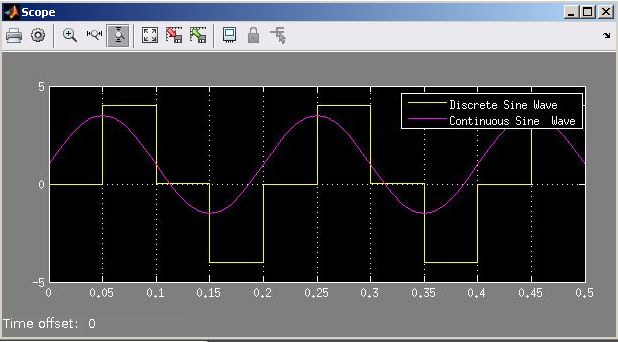
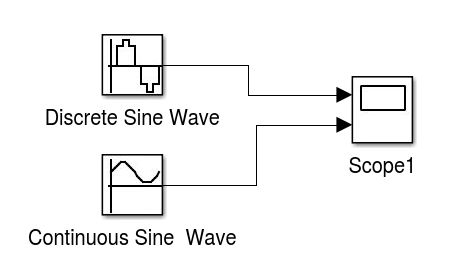
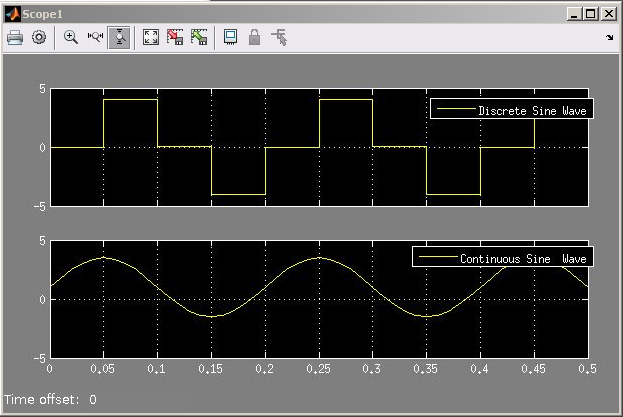
| AL2 - Exemplo de Simulink - Conhecendo o "Sine Wave" e o "Scope" |
|---|
f1 = 5; w1 = 2*pi*f1; sp = 4; ts = 1/(f1*sp);
|
3 Referências Bibliográficas:
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822