PSD29007-Engtelecom(2015-1) - Prof. Marcos Moecke
1 Registro on-line das aulas
1.1 Unidade 1
- Aula 1 (6 fev)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
- Resposta de sistemas LTI (Experimento 1.1)
- Amostragem de Sinais (Experimento 1.2)
- Uso do Matlab: Help, F9 executa o código destacado no Help. Programação com scripts .m, Execução de seções e variação de valores nos scripts,
- Ver também o Publish para a geração automática de relatórios em html, doc, pdf, latex ou ppt.
- Ver pag. 65 a 71 de [1]
- Ver PDF Documentation for MATLAB. Principalmente MATLAB Primer.
| Variação do Experimento 1.2 |
|---|
%% Experimento 1.2
fs = 10; Ts = 1/fs; fase = 0;
time = 0:Ts:(1-Ts);
f1 = 3; f2 = 7;
s_1 = cos(2*pi*f1*time+fase);
s_2 = cos(2*pi*f2*time+fase);
fsa = 1000; Tsa = 1/fsa;
time_aux = 0:Tsa:(1-Tsa);
figure(1);
stem(time,s_1,'ob');
hold on;
plot(time_aux, cos(2*pi*f1*time_aux+fase),'--k');
stem(time,s_2,'+r');
plot(time_aux, cos(2*pi*f2*time_aux+fase),'--m');
hold off;
legend('s_1 discreto','s_1 contínuo','s_2 discreto','s_2 contínuo')
Varie o valor da frequência de amostragem de 6 até 20 Hz e observe:
|
- Aula 2 (10 fev)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
| Variação do Experimento 2.2 |
|---|
%% Experimento 2.2
% Resposta em frequencia usando a função freqz
N = 1;
num = [1 0 0 0];
den = poly([0.8 0.2])
%den = [1 0.6 -0.16];
% modo 1
%[H,w]=freqz(num,den,[0:pi/100:N*pi-pi/100]);
%plot(w/pi, abs(H));
% modo 2
%[H,w]=freqz(num,den);
%plot(w/pi, abs(H));
% modo 3
%[H,w]=freqz(num, den, 'whole');
%plot(w/pi, abs(H));
% modo 4
freqz(num, den, 'whole');
figure(2);
zplane(num,den);
%% Resposta em frequencia substituindo z -> e^(jw)
syms z
Hf(z) = symfun(z^2/(z-0.2)/(z+0.8),z);
pretty(Hf)
latex(Hf)
N = 1;
w = [0:pi/100:N*pi-pi/100];
plot(w/pi,abs(Hf(exp(1i*w))))
%title(['$' latex(Hf) '$'],'interpreter','latex')
text(0.2,2,['H(z) = ' '$$' latex(Hf) '$$'],'interpreter','latex')
xlabel(['w/' '$$' '\pi' '$$'],'interpreter','latex')
|
- Aula 3 (13 fev)
- Revisão de Sinais e Sistemas no tempo discreto em Matlab:
1.2 Unidade 2
- Aula 4 (20 fev)
- Filtros Digitais: Filtros IIR:
- Aproximação de magnitude de filtros analógicos: do tipo Butterworth.
- Ver pag. 186 a 193 de [2]
- Aula 5 (24 fev)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros analógicos passa-baixas: do tipo Butterworth.
- Ver pag. 194 a 204 de [2]
- Aula 6 (27 fev)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros analógicos passa-baixas: do tipo Chebyshev I.
- Ver pag. 204 a 208 de [2]
- Aula 7 (3 mar)
- Filtros Digitais: Filtros IIR:
- Projeto de filtros analógicos passa-baixas: do tipo Chebyshev II.
- Uso das funções semilogx, semilogy,logspace, linspace.
- Ver em IIR Filter Design,
- Funçãos para projeto do filtro final (analógico com 's'): besself, butter, cheby1, cheby2, ellip
- Funções de estimação da ordem do filtro: buttord, cheb1ord, cheb2ord, ellipord
- Funções para projeto do filtro protótipo analógico passa-baixas: besselap, buttap, cheb1ap, cheb2ap, ellipap
- Funções de transformação de frequencia: lp2bp, lp2bs, lp2hp, lp2lp
- Transformação de frequência de filtros analógicos
- (passa-baixas -> passa-baixas, passa-baixas -> passa-altas, passa-baixas -> passa-faixa, passa-baixas -> rejeita-faixa)
- Ver pag. 208 a 218 de [2]
- Aula 8 (6 mar)
- Filtros Digitais: Filtros IIR: transformações do tempo contínuo no tempo discreto
- Transformação invariante ao impulso (apenas para filtros com forte atenuação em frequência altas, ex: passa-baixas e passa-faixa)
- Transformação bilinear (para todos tipos de filtro)
- Ver em IIR Filter Design,
- Filter discretization functions: bilinear, impinvar
1.3 Unidade 3
- Aula 9 (10/mar)
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: simétricos e antisimétricos
- Ver pag. 249 a 256de [2]
- Aula 10 (13/mar)
- Filtros Digitais: Filtros FIR
- Filtros de fase linear: propriedades
- Ver pag. 256 a 260 de [2]
- Aula 11 (17/mar)
- Filtros Digitais: Filtros FIR
- Coeficientes da série de Fourier de filtros ideias: LP, HP, BP, BS
- Passa-baixas (Low-pass)
- Passa-altas (High-pass)
- Passa-faixa (Band-pass)
- Rejeita-banda (Band-stop)
- Janela retangular, fenômeno de Gibbs
- Aula 12 (18/mar)
- Filtros Digitais: Filtros FIR
- Uso de funções de janelamento temporal no projeto de filtros digitais.
- Tipos de janelas temporais usadas no projeto de filtros digitais.
- Retangular
- Bartlett
- Hanning
- Hamming
- Blackman
- em todas as janelas quando
- Projeto de filtro FIR utilizando janelas temporais
- Uso de janelas fixas no Matlab : rect, triang, bartlett, hann, hamming, blackman, blackmanharris, nuttall.
L = 64;
wvtool(rectwin(L), triang(L), bartlett(L), hann(L), hamming(L), blackman(L), blackmanharris(L), nuttallwin(L));
L = 64;
r = 60; % Chebyshev e Tukey
alpha = 3; % Gauss
betha = 8; % Kaiser
nbar = 10; % Taylor
wvtool(kaiser(L,betha), chebwin(L,r), gausswin(L,alpha),tukeywin(L,r), taylorwin(L,nbar,-r));
- Ver pag. 266 a 273 de [2]
- Aula 13 (24/mar)
- Filtros Digitais: Filtros FIR
- Projeto de filtro com splines.
- Passa-baixas (Low-pass)
- Aula 14 (25/mar)
- Filtros Digitais: Filtros FIR
- Filtro Equiripple com fase linear (Parks and McClellan)
- Uso das funções do Matlab para projeto de filtro equiripple firpmord e firpm.
- Projetar os seguintes filtros (frequencias em rad/s e rejeição em dB)
- Passa-faixa: wr1 = 0.2, wp1 = 0.4, wp2 = 0.6, wr2 = 0.75, rr = 40, rp = 0.2.
- Passa-faixa: wr1 = 0.2, wp1 = 0.4, wp2 = 0.6, wr2 = 0.7, rr = 40, rp = 0.2.
- Passa-baixas: wp = 0.4, wr = 0.7, rr = 40, rp = 0.2.
- Passa-altas: wp = 0.7, wr = 0.4, rr = 40, rp = 0.2.
- Estudar Practical Introduction to Digital Filter Design, Using FDATool
- Aula 15 (30/mar)
- Filtros Digitais: Filtros FIR
- Aula Prática: Uso do Fdatool para projeto de filtro IIR, FIR equiripple e FIR com janela.
1.4 Unidade 4
- Aula 16 (1/04)
- Realização de Filtros
- Realização de filtros FIR: Forma Direta I, Transposta, Cascata, Polifase, filtros de fase linear simétrico e antissimétrico.
- Estudar estrutura de filtros disrcetos FIR no Matlab.
- Ver pag. 303 a 312 de [2].
- Aula 17 (7/04)
- Realização de Filtros IIR
- Bloco de IIR de 2ª ordem.
- Separando H(z) em dois blocos , e obtendo o sinal intermediário W(z)
- Podemos obter a realização de na forma direta.
- Para obter a realização de , é necessário reescrever a saída em função de e das saídas anteriores e :
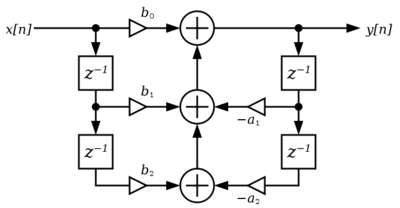
- Com o ordenamento dos blocos e em ordem direta teremos a Forma Direta I:
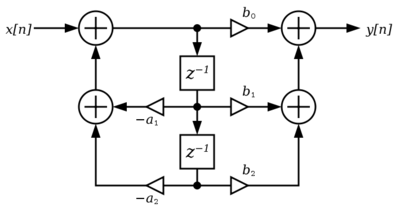
- Com o ordenamento dos blocos e em ordem reversa teremos a Forma Direta II (Canônica):
- Realização de filtros IIR: Forma Direta I e II, Transposta, Cascata, Paralela
- Ver funções do Matlab: roots, poly, residuez, tf2zp, zp2tf, zp2sos, tf2sos, tf2latc.
- Implementar o exercício 6.3: Forma direta I, Forma direta II, Cascata.
- Implementar o exercício 6.13: Forma direta I, Cascata e Paralela.
- Ver pag. 313 a de 353 [2].
- Ver pag. 469 a 474 do Lathi [3]
- Aula 18 (08/04)
- Realização de Filtros
- Aula 19 (14/04)
- Realização de Filtros
- Aula 20 (15/04)
- Realização de Filtros
- Aula 21 (22/04)
- Projeto e realização de Filtros IIR x FIR
- Ver AE5 (Prazo de entrega 11/05/2015)
- Aula 22 (28 abr)
- Projeto de Filtros IIR x FIR
- Ver Atividade AE5.
- Aula 23 (29 abr)
- Atraso de grupo em filtros IIR e FIR no Matlab.
- Filtro com fase nula
- Ver atividade livre AL4.
- Aula 24 (5 mai)
- Projeto de filtros Passa-Tudo para equalizar a fase (atraso de grupo) de filtros IIR.
- Projetar filtros Passa-tudo que equalizam a fase na faixa de passagem do filtro
- Ver funções isallpass, iirgrpdelay, conv.
- Estudar os quatro exemplos de [1] pag.2-56 a 2-63.
- Obter o filtro cascata através da multiplicação dos polinômios do numerador e denominador.
- Ler: Lang, M.; Laakso, T.I., "Simple and robust method for the design of allpass filters using least-squares phase error criterion," Circuits and Systems II: Analog and Digital Signal Processing, IEEE Transactions on , vol.41, no.1, pp.40,48, Jan 1994
- Aula 25(6 mai)
- Filtros de fase mínima, fase máxima e mistos.
- Ver fase mínima,
- Aula 26(12 mai)
-
- Implementação de um filtro equalizador do atraso de grupo para o projeto AE-5
1.5 Unidade 5
- Aula 27(13 mai)
-
- Uso do Simulink
- Aula 28(19 mai)
-
- Uso do Simulink
-
-
- Introduction: What Is Simulink? 4:42
- Constructing and Running a Simple Model 13:45
- Simulating a Model 10:10
- Working with MATLAB 9:12
- Creating Subsystems 6:46
- É importante ler informações complementares sobre o Solver Pane, Model Simulation, Choose a Solver
-
- Aula 29, 30 (20 e 26 mai)
-
- Uso do Simulink
-
-
- Modeling Discrete Dynamical Systems 19:35
- Use Signal Processing Blockset 12:01
- dspstartup.m command
- Working with Signals in Simulink 9:59
- É importante ler informações complementares sobre, Tempo de amostragem (Time Sample), View Sample Time Information, Sample- and Frame-Based Concepts, Vector Concatenate, Matrix Concatenate.
-
- Aula 31 (27 mai)
-
- Visita aos equipamento da RNP na UFSC -> prof Sandro Lima.
- Aula 32 (2 jun)
-
- Uso do Simulink
-
-
- Applying a Filter 9:04
- Designing and Implementing a Filter 10:23
-
- Aula 33 (3 jun)
-
- Exemplos de uso do Simulink:
- Cancelamento de Ruido usando Filtragem adaptativa LMS.
SP_adaptiveFilt
- Remoção dos Lyrics de um arquivo de música com voz centrada em canal estéreo.
SP_lyricRemoval
- Conversão da taxa de amostragem de um sinal de audio.
dspaudiosrc
- Realizar Atividade de Avaliação AE7.
- Aula 34 e 35 (9 e 10 jun)
-
- Uso do HDL Coder
- Getting Started with MATLAB to HDL Workflow
- Basic HDL Code Generation with the Workflow Advisor
- Floating-Point to Fixed-Point Conversion
- Verify HDL Model with MATLAB Testbench
- Ver também o uso da função fi - Construct fixed-point numeric object
a = fi(-1, true, 8, 0) a.bin
a = fi(-128, true, 8, 0) a.bin
a = fi(127, true, 8, 0) a.bin
- Ver também a função resize da ieee.numeric_std library.
function RESIZE (ARG: SIGNED; NEW_SIZE: NATURAL) return SIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with the sign bit (ARG'LEFT). When truncating,
-- the sign bit is retained along with the rightmost part.
function RESIZE (ARG: UNSIGNED; NEW_SIZE: NATURAL) return UNSIGNED;
-- Result: Resizes the SIGNED vector ARG to the specified size.
-- To create a larger vector, the new [leftmost] bit positions
-- are filled with '0'. When truncating, the leftmost bits
-- are dropped.
- Aula 36 (16 jun)
-
- Uso do HDL Coder
- Simulação do projeto da aula anterior no ModelSim-ALTERA.
| Procedimentos para a Simulação |
|---|
|
Abra o ModelSim: /opt/altera/13.0sp1/modelsim_ase/bin/vsim & Troque a pasta de trabalho para a pasta onde o Matlab gerou os arquivos .vhd e .do [File > Change Directory] ou digite na janela tcl: cd /tmp/mlhdlc_sfir/codegen/mlhdlc_sfir/hdlsrc Execute o arquivo do mlhdlc_sfir_fixpt_tb_compile.do Edite o arquivo mlhdlc_sfir_fixpt_tb_sim.do, comentando as linhas que forçam a saida do Modelsim. Estas linhas foram criadas para a integração direta com o Matlab, mas ela não funciona com a versão do ModelSim que temos disponível. edit mlhdlc_sfir_fixpt_tb_sim.do #onerror {quit -f}
#onbreak {quit -f}
...
#quit -f
Agora execute o arquivo mlhdlc_sfir_fixpt_tb_sim.do, o qual irá adicionar os sinais a serem analisados na janela Wave e executará todos os comandos vhdl do arquivo *_tb.vhdl gerado pelo Matlab. do mlhdlc_sfir_fixpt_tb_sim.do Ao tinal da simulação a janela Transcript indicará se o teste passou: # ** Note: **************TEST COMPLETED (PASSED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb ou se falhou: # ** Note: **************TEST COMPLETED (FAILED)************** # Time: 20030 ns Iteration: 1 Instance: /mlhdlc_sfir_fixpt_tb Note ainda que os sinais de entrada (x_in), os sinais de saída (y_out e delayed_xout) e os dois sinais de referência gerados na simulação com o Matlab (y_out_ref e delayed_xout_ref) são mostrados como sequências de bits. Para melhorar a visualização mude o Formato desses sinais para analógico [Clique Direito do Mouse> Format > Analog (automatic)]. |
| Problemas na integração Matlab - Modelsim |
|---|
sudo gedit quartus
|
- Referência:
- Simulink® Getting Started Guide.
- HDL Coder™ Getting Started Guide.
- Consultar outros documentos sobre o Simulink no site da Mathworks.
1.6 Unidade 6
- Aula 37 a 40 (17/06 a 30/06)
- Projeto Final
- Implementação de filtros em VHDL usando o HDL Coder para projeto e Modelsim para Simulação
- Os alunos trabalharam de forma individual na realização e implentação do filtro projeto anteriormente na atividade AE5.
- Ao final do projeto cada aluno deve apresentar:
- o arquivo de projeto do HDL Coder com os códigos ".m";
- o arquivos em VHDL do filtro e seu testbench;
- o arquivo ".do" para a simulação com Modelsim;
- um artigo técnico completando o artigo iniciado no item AE5.
1.7 Avaliações
- Entrega dos diversos trabalhos ao longo do semestre AE1 a AE4.
- Entrega do artigo sobre a atividade AE5 (27%)
- Projeto Final. O projeto é avaliado nos quesitos: 1) Implementação do Sistema, 2) Documentação, 3) Avaliação Global do aluno no projeto. (40% do conceito)
2 Atividades extra
2.1 PARA ENTREGAR
2.2 JÁ ENCERRADAS
| AE1 - Experimento 3.2 (Prazo de entrega 23/02/2015) |
|---|
|
| AE2 - Projeto de Filtro Analógicos (Prazo de entrega 09/03/2015) |
|---|
|
| AE3 - Projeto de Filtro Digitais IIR (Prazo de entrega 23/03/2015) |
|---|
%% Variação do Experimento 6.1 - DINIZ
% Parâmetros do filtro digital passa-faixa
Ap = 0.5; % Atenuação máxima na banda de passagem
Ar = 65; % Atenuação mínima na banda de rejeição
Ws = 10000; Fs = Ws/(2*pi); Ts = 1/Fs; % Frequência de amostragem (Ws -> rad/s e Fs -> Hz), e período de amostragem
wr1 = 850; wr2 = 1150; % Frequências de rejeição (rad/s) normalizada em relação a Ws/2
wp1 = 980; wp2 =1020; % Frequências de passagem (rad/s) normalizada em relação a Ws/2
% Cálculo do filtro digital passa-faixa usando transformação bilinear
wnr1 = wr1/(Ws/2); wnr2 = wr2/(Ws/2); wr =[wnr1 wnr2];
wnp1 = wp1/(Ws/2); wnp2 =1020/(Ws/2); wp = [wnp1 wnp2];
[n wn] = ellipord(wp, wr, Ap, Ar);
[b a] = ellip(n,Ap,Ar,wp);
[H, w] = freqz(b,a,10000);
fi = 0; ff = Ws/2; % fi = 850*0.95; ff = 1150*1.05;
subplot(311); plot(w*Fs,abs(H)); grid on; xlim([fi,ff]);
subplot(312); plot(w*Fs,angle(H)); grid on; xlim([fi,ff]);
[gd,w] = grpdelay([b a], 10000);
subplot(313); plot(w*Fs,gd); grid on; xlim([fi,ff]);
figure; zplane([b,a]);
%% Análise do filtro usando um cosenso puro
t = 0:Ts:(1-Ts);
ti =0; tf= 1; % ti=0.5; tf=0.6;
w1 = 800;
x1 = cos(w1*t);
y1 = filter(b,a,x1);
figure; plot(t,x1,'k',t,y1,'b'); ylim([-1.5 1.5]), xlim([ti tf]);
|
| AE4 - Projeto de Filtro Digitais FIR - parte 1 (Prazo de entrega 30/03/2015) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| AE5 - Projeto de Filtro Digitais FIR x IIR (Prazo de entrega 15/05/2015) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| PROJETO FINAL - Implementação de Filtros em VHDL (Prazo de entrega 06/07/2015) |
|---|
|
2.3 ESTUDOS SEM ENTREGA DE DOCUMENTAÇÃO
| AL1 - Resposta em frequência a partir da posição dos pólos-zeros |
|---|
|
| AL2 - Resposta em frequência em Sistemas de Tempo Discreto |
|---|
|
| AL3 - Desempenho do código de uma FFT |
|---|
N = 10000;
%% tamanho do vetor de 1015 -> 5 x 7 x 29
N0 = 1015;
y1 = rand(N0,1);
tic; for k = 1:N; Y1 = fft(y1)/N0; end; toc
%% tamanho do vetor de 1019 -> primo
N_0 = 1019;
y2 = [y1; zeros(N_0-N0,1)];
tic; for k = 1:N; Y2 = fft(y2)/N_0; end; toc
%% tamanho do vetor de 1024 -> 2^10
N_0 = 1024;
y3 = [y1; zeros(N_0-N0,1)];
tic; for k = 1:N; Y3 = fft(y3)/1024; end; toc
|
| AL4 - Atraso de grupo em filtros IIR e FIR no Matlab |
|---|
%% Carregando um sinal de ECG com ruído com duração de 4 segundos.
load noisyecg.mat
x = noisyECG_withTrend;
fa = 500; %% 2000 amostras em 4 segundos => 500 amostras por segundo.
t = [0:length(x)-1]*1/fa;
plot(t,x);
%% Projetando um filtro passa-baixa tipo IIR butter com f_passagem = 0.15 rad/s
d = designfilt('lowpassiir', ...
'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
'PassbandRipple',1,'StopbandAttenuation',60, ...
'DesignMethod','butter');
freqz(d)
%% Filtro de x revertido x e somando com x filtrado. OFF LINE
y = flip(filter(d,flip(filter(d,x))));
y1 = filter(d,x);
figure(2);
subplot(2,1,1)
plot(t, [y y1])
title('Filtered Waveforms')
legend('Zero-phase Filtering','Conventional Filtering')
subplot(2,1,2)
plot(t, [x y])
title('Original Waveform')
legend('noisy ecg ','fitered ecg')
%% Projetando um filtro passa-baixa tipo FIR equiripple com f_passagem = 0.15 rad/s
d = designfilt('lowpassfir', ...
'PassbandFrequency',0.15,'StopbandFrequency',0.2, ...
'PassbandRipple',1,'StopbandAttenuation',60, ...
'DesignMethod','equiripple');
y = flip(filter(d,flip(filter(d,x))));
y1 = filter(d,x);
gd = grpdelay(d);
gd1 = ceil(gd(1));
y = [y1(gd1:end); zeros(gd1-1, 1)];
O cálculo do atraso de grupo pode ser realizado utilizando a função grpdelay ou diretamente pela definição da derivada do ângulo em relação a frequência: %% Calculo do atraso de grupo
% Método 1 - uso da função grpdelay
[z,p,k] = butter(30,0.2);
sos = zp2sos(z,p,k);
[gd,w]=grpdelay(sos,128);
figure(1)
plot(w/pi,gd),grid on;
% Método 2 - derivada obtida por aproximação discreta
% calculo a cada par de pontos (w2-w1)/delta_w
[h,w] = freqz(sos);
a = unwrap(angle(h));
hold on; plot(w/pi,a,'g');
delta_w = pi/length(a);
plot(w(1:end-1)/pi+delta_w/2,-(a(2:end)-a(1:end-1))/delta_w,'r');
|
3 Referências Bibliográficas
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 DINIZ, P. S. R., DA SILVA, E. A. B., e LIMA NETTO, S. Processamento Digital de Sinais: Projeto e Análise de Sistemas. 2. ed. Porto Alegre: Bookman, 2014. 976 p. ISBN 978-8582601235
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 SHENOI, B. A. Introduction to Digital Signal Processing and Filter Design. 1.ed. New Jersey: John Wiley-Interscience, 2006. 440 p. ISBN 978-0471464822
- ↑ 3,0 3,1 3,2 3,3 LATHI, Bhagwandas P. Sinais e Sistemas Lineares. 2. ed. Porto Alegre: Artmed-Bookman, 2007. 856 p. ISBN 978-8560031139