Curso Matlab aplicado ao processamento de imagens
Esta é a página do curso avançado de Matlab, elaborado pelo professor Diego da Silva de Medeiros dentro do projeto intitulado MATLAB - Software de estudos matemáticos. Este curso visa complementar o primeiro curso, de nível básico, com técnicas mais avançadas. O curso foi dividido de 3 encontros de 2 horas:
- Nesta aula, conceitos do Matlab não compreendidos no curso básico serão apresentados:
- Indexação de matrizes
- Classes de dados
- Funções
- Exceções
- Exercícios
- Nesta aula, a criação de interfaces gráficas simples para scripts será apresentada.
- Botões de ação
- Eixos
- Campos de texto
- Radiobuttons
- Nesta aula, técnicas simples de processamento de imagens serão estudadas:
- Negativo da imagem
- Brilho
- Contraste
- Binarização
- Marca d'água
- Suavização
- Detecção de bordas
- Paleta de cores
1 Curso Matlab aplicado ao processamento de imagens - Aula 1
1.1 Indexação de matrizes
1.1.1 Indexação simples
Uma das maiores barreiras do usuário do Matlab é a compreensão da indexação de variáveis. A indexação é realizada com parênteses e o número da linha/coluna/etc que se deseja acessar. Para entender isso, vamos criar 3 variáveis, um vetor linha, um coluna e uma matriz:
>> lin = [1 2 3 4]; >> col = [5; 6; 7; 8]; >> mat = [1 2 3 4; 5 6 7 8];
Se quisermos acessar o 1º elemento dos vetores, basta usar a sintaxe variavel(1):
>> lin(1)
ans =
1
>> col(1)
ans =
5
Da mesma forma, podemos acessar o primeiro elemento da matriz (linha 1, coluna 1):
>> mat(1,1)
ans =
1
Repare que para o Matlab, o primeiro elemento de uma variável é o elemento de número 1. Isso vai contra algumas linguagens de programação, como o C, onde o primeiro elemento é o de número 0.
1.1.2 Indexação múltipla
Podemos também acessar mais de um elemento de vetores, passando um vetor como índice:
>> lin([1, 3])
ans =
1 3
>> col([1, 3])
ans =
5
7
Repare que a configuração dos elementos retornados (linha ou coluna) segue a configuração dos vetores originais. Para acessar mais de um elemento de uma matriz, passamos dois vetores, um com as linhas e o outro com as colunas:
>> mat([1, 2], [2, 4])
ans =
2 4
6 8
1.1.3 Uso do ":"
Tanto para matriz quanto para vetores, podemos usar o operador dois pontos para facilitar a sintaxe:
>> col(1:3)
ans =
5
6
7
>> mat(1:2, 2:4)
ans =
2 3 4
6 7 8
Neste caso, como a matriz mat tem apenas duas linhas, poderíamos substituir o 1:2 simplesmente pelos dois pontos:
>> mat(:, 2:4)
ans =
2 3 4
6 7 8
1.1.4 O comando end
Muitas vezes não sabemos o número total de elementos de um vetor ou de uma matriz, e queremos pegar todos os elementos a partir de uma determinada posição. Para isso há a facilidade do comando end, que indica que os dados da variável deverão ser tomados até o último elemento:
>> mat(:, 2:end)
ans =
2 3 4
6 7 8
1.1.5 Índice versus Subscrito
Ao ler os comandos acima, repare que há então formas diferentes de se indexar uma variável: um vetor recebe apenas um número, que indica o número do elemento, e uma matriz recebe dois números, que indica a linha e a coluna do elemento. Quando passamos apenas um número dizemos que estamos escolhendo os elementos pelo seu índice, e quando passamos dois ou mais números estamos escolhendo os elementos pelo seu subscrito. Esse é um fator de confusão no Matlab, pois podemos inverter as coisas e escolher elementos de um vetor via subscrito e elementos de uma matriz via índice:
>> lin(1,3)
ans =
3
>> col(2,1)
ans =
6
>> mat(4)
ans =
6
Assim, é selecionado o elemento da linha 1 e coluna 3 do vetor lin, o elemento da linha 2 e coluna 1 do vetor col. No caso da matriz, como o número de dimensões da variável é maior que o número de números passados, o Matlab entende que os elementos estão sendo selecionados via índice, e conta, coluna a coluna, os índices dos elementos até chegar o índice desejado. Como estamos selecionando o elemento 4 da matriz, o matlab passa os elementos mat(1) = 1, mat(2) = 5, mat(3) = 2 e para no mat(4) = 6. Isso pode ser visto ao selecionar os elementos de 1 a 4 da matriz:
>> mat(1:6)
ans =
1 5 2 6 3 7
Repare que o resultado da seleção dos elementos de 1 a 4 da matriz é um vetor linha com os valores de mat(1,1), mat(2,1), mat(1,2), mat(2,2), mat(1,3) e mat(2,3). Porém, ao usar a escolha pelo índice, podemos também receber um vetor coluna, desde que o vetor usado como índice seja um vetor coluna:
>> mat([1; 2; 3; 4; 5; 6])
ans =
1
5
2
6
3
7
Mais do que isso, podemos ter como resultado uma matriz:
>> mat([1 2; 3 4; 5 6])
ans =
1 5
2 6
3 7
ou mesmo ter, a partir de um vetor, uma matriz como resultado:
>> col([1 3; 2 4; 1 4; 2 3])
ans =
5 7
6 8
5 8
6 7
1.2 Classes de dados
No curso de nível básico, classes numéricas de dados foram estudados. Nesta etapa iremos conhecer outras classes existentes:
1.2.1 Char
Nos dados de tipo char estão compreendidos os caracteres textuais. Para indicar que uma variável é do tipo char, usamos aspas simples:
>> var1 = 'a' var1 = a
Da mesma forma que números, vetores de dados char podem ser criados:
>> var2 = ['a', 'b', 'c'] var2 = abc
Repare que um vetor de caracteres é uma string, e a sua criação pode ser feita diretamente, inclusive sem os colchetes:
>> var3 = 'ola amiguinhos!' var3 = ola amiguinhos!
1.2.1.1 Concatenação de caracteres e números
O Matlab faz uso da Tabela ASCII quando um número é concatenado à um dado da classe char:
>> var4 = ['a' 35] var4 = a#
Porém, é possível converter o número em um vetor char, não realizando a conversão. Para isso é usada a função num2str:
>> var5 = ['a' num2str(35)] var5 = a35
1.2.2 Cell
1.2.2.1 O problema
Muitas vezes, queremos criar listas de nomes, e a primeira opção que temos é usar strings:
>> lista1 = ['Jose Aparecido'; 'Maria Silveira'; 'Etevaldo Mario'] lista1 = Jose Aparecido Maria Silveira Etevaldo Mario
Este tipo de solução, porém, funciona apenas quando todas as strings tem o mesmo número de caracteres, pois em suma, o que estamos fazendo é uma matriz de dados do tipo char:
>> size(lista1)
ans =
3 14
Se tentarmos criar uma lista com strings de tamanhos diferentes, estamos criando uma matriz com número de elementos incompletos, sendo retornado um erro:
>> lista2 = ['mae'; 'pai'; 'filho'] Error using vertcat Dimensions of matrices being concatenated are not consistent.
1.2.2.2 A classe cell
Para resolver este e outros problemas, o Matlab disponibiliza uma classe de dados adicionais, a cell. O tipo cell é como um invólucro que armazena dados de outros tipos do Matlab. Sua criação é feita usando chaves ao invés de colchetes:
>> celula1 = {5}
celula1 =
[5]
>> celula2 = {'b'}
celula2 =
'b'
>> celula3 = {[1, 2, 3, 4, 5]}
celula3 =
[1x5 double]
>> celula4 = {'boa noite'}
celula4 =
'boa noite'
Repare que todas as variáveis criadas são do tipo cell, independente de estarem armazenando números ou letras:
>> whos celula1 celula2 celula3 celula4 Name Size Bytes Class Attributes celula1 1x1 120 cell celula2 1x1 114 cell celula3 1x1 152 cell celula4 1x1 130 cell
Além disso, todas as variáveis criadas tem o mesmo tamanho, 1x1. Porém, assim como qualquer outro tipo de dado do Matlab, vetores ou matrizes podem ser criados.
>> celula5 = {1, 2, 3, 4}
celula5 =
[1] [2] [3] [4]
>> celula6 = {'g'; 'y'; 'A'}
celula6 =
'g'
'y'
'A'
>> celula7 = {[1 2], [3; 4]}
celula7 =
[1x2 double] [2x1 double]
>> celula8 = {'oi', 'amigo'}
celula8 =
'oi' 'amigo'
>> whos celula5 celula6 celula7 celula8
Name Size Bytes Class Attributes
celula5 1x4 480 cell
celula6 3x1 342 cell
celula7 1x2 256 cell
celula8 1x2 238 cell
Um dado da classe cell pode agrupar dados de diferentes tamanhos e classes:
>> celula9 = {'Joao', 13, 'O+', [140, 35]; 'Maria', 15, 'A-', [135, 29]}
celula9 =
'Joao' [13] 'O+' [1x2 double]
'Maria' [15] 'A-' [1x2 double]
1.2.3 Structs
As cells permitem criar listas com tipos diferentes de dados e com diferentes tamanhos. Porém, é algumas vezes necessária a criação de listas mais elaboradas. Para isso, structs podem ser utilizadas. Para criar um dado do tipo struct, pode-se usar a função struct:
>> s1 = struct('Nome',[],'Idade',[],'Tipo',[],'Altura',[],'Peso',[])
s1 =
Nome: []
Idade: []
Tipo: []
Altura: []
Peso: []
Neste caso, uma struct com 5 campos foi criada, porém, nenhum valor foi atribuído à nenhum dos campos. Para adicionar valores, o operador ponto é utilizado:
>> s1.Nome = 'Joao'
s1 =
Nome: 'Joao'
Idade: []
Tipo: []
Altura: []
Peso: []
>> s1.Altura = 140
s1 =
Nome: 'Joao'
Idade: []
Tipo: []
Altura: 140
Peso: []
É possível atribuir valores já na criação da struct, bastando incluir no lugar dos colchetes. Além da função struct é possível criar variáveis desta classe dinamicamente, através do operador ponto:
>> s2.Marca = 'Volkswagen'
s2 =
Marca: 'Volkswagen'
>> s2.Modelo = 'Fusca'
s2 =
Marca: 'Volkswagen'
Modelo: 'Fusca'
>> s2.Ano = 1962
s2 =
Marca: 'Volkswagen'
Modelo: 'Fusca'
Ano: 1962
A criação de uma lista é feita a partir de um vetor de structs:
>> s2(2).Marca = 'FIAT';
>> s2(2).Modelo = '147';
>> s2(2).Ano = 1980
s2 =
1x2 struct array with fields:
Marca
Modelo
Ano
1.3 Funções
1.3.1 Argumento e retorno simples
Assim como a maioria das linguagens de programação o Matlab também permite a criação de funções. Com elas, evitamos a repetição de códigos numa simulação, contribuindo para a legibilidade e facilitando a alteração de funcionalidade. Para criar uma função criamos um arquivo com o nome pretendido e incluímos um cabeçalho que indica as suas características.
Por exemplo, arquivo soma1.m:
function y = soma1(x) y = x + 1; end
Este arquivo cria uma função que soma 1 à um número. Esse número é passado como argumento da função (x), e o resultado da soma é retornado através da variável y. O comando end ao fim do arquivo é neste caso opcional. Após salvar as alterações no arquivo, basta chamar a função pelo seu nome e lista de argumentos:
>> soma1(2)
ans =
3
>> soma1(5)
ans =
6
>> soma1(1998)
ans =
1999
1.3.2 Argumento e retorno múltiplo
Uma função também pode receber e retornar mais de um valor. Neste caso, o seu cabeçalho fica um pouco diferente:
function [soma, subt, mult, divs] = operacoes(x1, x2) soma = x1 + x2; subt = x1 - x2; mult = x1 * x2; divs = x1 / x2; end
Esta função recebe dois números (x1 e x2) e realiza 4 operações. Cada operação é retornada numa variável diferente. Um detalhe importante é que o acesso aos múltiplos retornos da função se dá apenas via atribuição à variáveis específicas. Do contrário, apenas a primeira variável (no caso, a soma) é retornada:
>> operacoes(1,2)
ans =
3
>> [soma, subt] = operacoes(1,2)
soma =
3
subt =
-1
>> [soma, subt, mult, divs] = operacoes(1,2)
soma =
3
subt =
-1
mult =
2
divs =
0.5000
1.3.3 Variáveis locais e globais
Todas as variáveis criadas dentro de uma função são visíveis apenas à ela. São variáveis locais. Da mesma forma, uma função acessa do workspace apenas as variáveis que lhe foram passadas como argumento. É possível estender o uso de uma variável do workspace para qualquer função, usando para isso o comando global. Após a execução do comando global var, a variável var poderá ser usada por qualquer função.
1.3.4 Funções inline
Uma forma rápida de criar funções simplificadas é através do comando inline:
>> f = inline('x + y','x','y')
f =
Inline function:
f(x,y) = x + y
No quadro acima, a função f(x,y), que calcula a soma da variável x com a variável y foi criada. A função é acessada a partir da variável ao qual ela foi atribuída (neste caso, f), e parâmetros são passados como uma função qualquer:
>> f(1,2)
ans =
3
1.4 Exceções
Ao desenvolver uma simulação, podem acontecer erros de indexação, divisões por zero, ou outros problemas. Em alguns desses casos, sabemos que esses erros vão acontecer, mas não há outra forma de desenvolver o programa. O seguinte bloco de código exemplifica isso:
>> var = 15:18
var =
15 16 17 18
>> for i = 1:6
x = var(i)
end
x =
15
x =
16
x =
17
x =
18
Attempted to access var(5); index out of bounds because numel(var)=4.
Repare que um erro foi retornado após o programa tentar acessar o 5º elemento de um vetor de tamanho 4.
Para casos como esse há no Matlab o tratamento de exceção, através dos comandos try e catch. Digamos no exemplo acima, a aplicação aceite que ao atingir o final da variável, atribuamos o valor 0 à variável x. Com o tratamento de exceção, isto seria resolvido da seguinte forma:
for i = 1:6
try
x = var(i)
catch
x = 0
end
end
O Matlab tenta acessar o elemento i da variável var para atribuir à variável x. Caso ele não consiga, ele executa o bloco de código catch, que atribui o valor 0 à variável x. O resultado deste código é:
x =
15
x =
16
x =
17
x =
18
x =
0
x =
0
1.5 Exercício
Objetivo geral
Desenvolver um programa que recebe uma lista de dados de alunos de uma escola e gera um relatório. Os dados estarão em forma de uma tabela, onde as colunas são: Matrícula, Nome, Idade, Curso, Turma, Turno, Situação.
Etapas
- A tabela de entrada estará em forma de uma matriz do tipo cell, construir uma função que converte a tabela cell num vetor struct com os campos correspondentes
- A geração do relatório deverá usar os dados na forma de struct
- dados.zip - Arquivo com os dados dos alunos, para carregamento no Matlab.
- resposta.m - Arquivo com a solução do exercício.
2 Curso Matlab aplicado ao processamento de imagens - Aula 2
Nesta aula vamos aprender a criar interfaces simples para scripts.
O Matlab possui uma ferramenta para simplificar a criação de GUIs, o GUIDE. Neste curso, vamos criar uma interface simples, com dois eixos de plot, um campo de entrada de dados, dois botões de radio e um botão de apertar. No primeiro eixo vamos plotar um seno, e no segundo vamos plotar um cosseno ou uma tangente, dependendo do botão de radio marcado. A frequência da senoide será inicialmente 0, mas poderá ser alterada através do campo de dado.
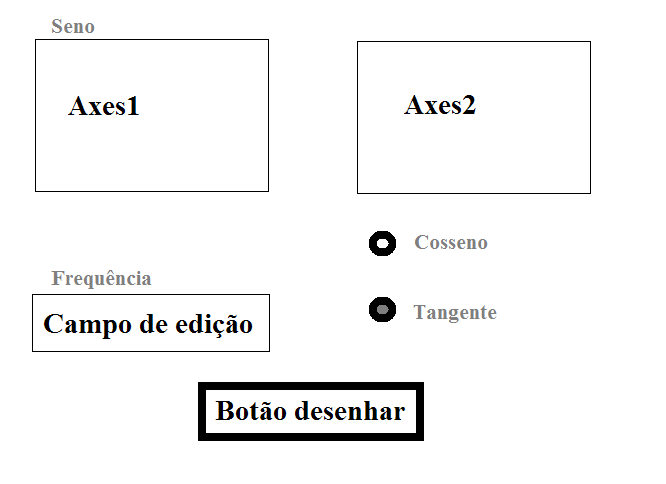
2.1 Criação da interface
Para iniciar a criação da interface, escolha a pasta que você quer que os arquivos estejam salvos e digite na janela de comandos:
>> guide
Na janela quick start que apareceu, escolha Blank GUI e pressione OK.
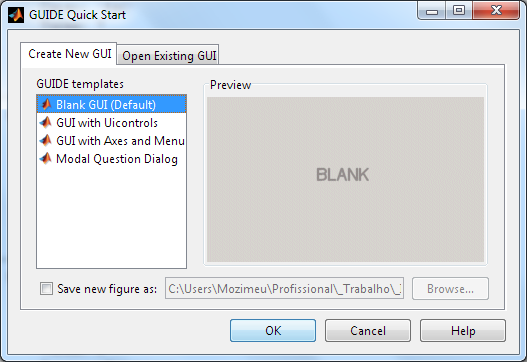
A janela que se abre é o editor de interfaces. É aí que os botões são dispostos na janela. Para adicionar uma componente, basta clicar no botão na parte esquerda e arrastá-lo para a parte central, na posição desejada. Cada componenteadicionada possui atributos, que podem ser visualizados através de um duplo clique:
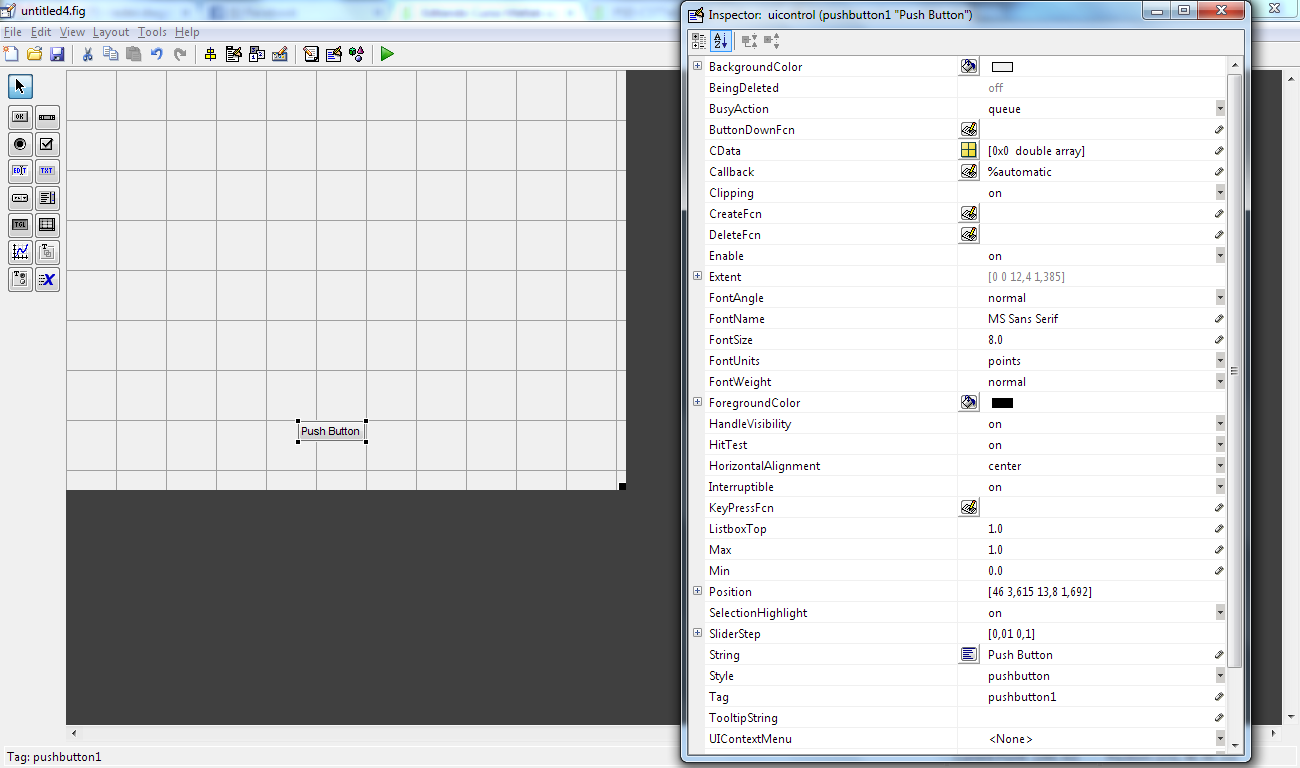
Inicie com a criação de 3 painéis, como dispostos na figura:
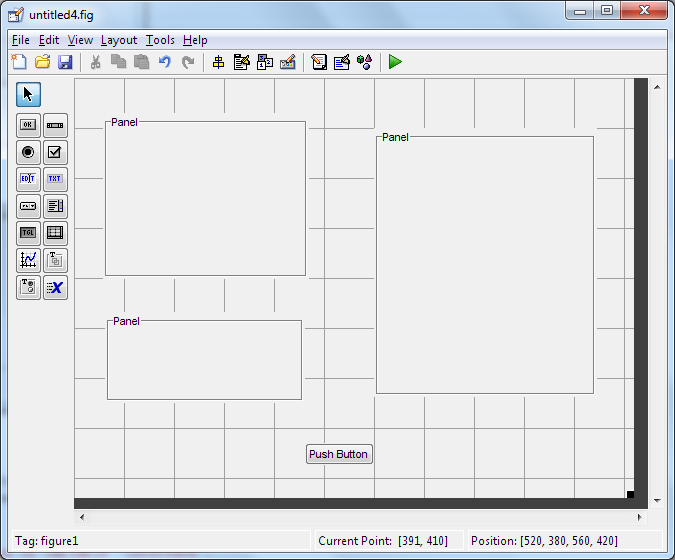
Inclua 2 axes nos painéis superior esquerdo e direito:
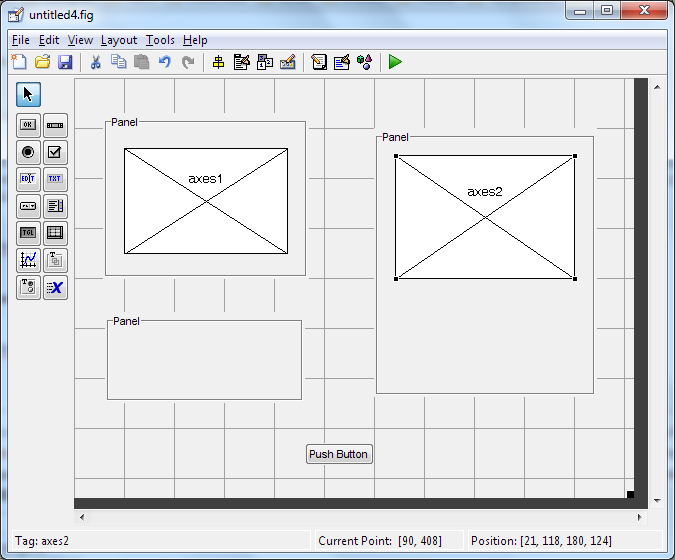
Por fim, inclua um campo edit text no painel inferior esquerdo dois radiobuttons na parte inferior do painel direito:
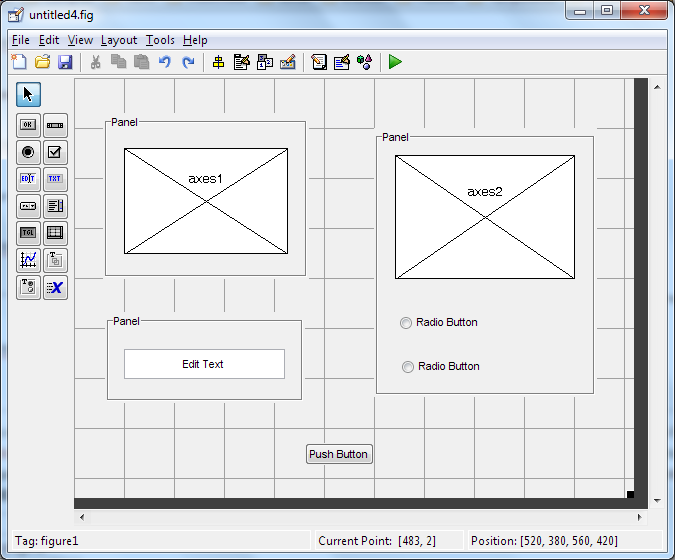
É possível alterar as informações escritas na interface, clicando duas vezes na componente e alterando o campo Title, no caso dos painéis, ou String para os demais. A interface concluída pode ser vista abaixo:

Salve o arquivo com o nome interface, uma janela com vários códigos irá aparecer. Ao digitar na janela de comando o comando interface, a janela da interface se abrirá.
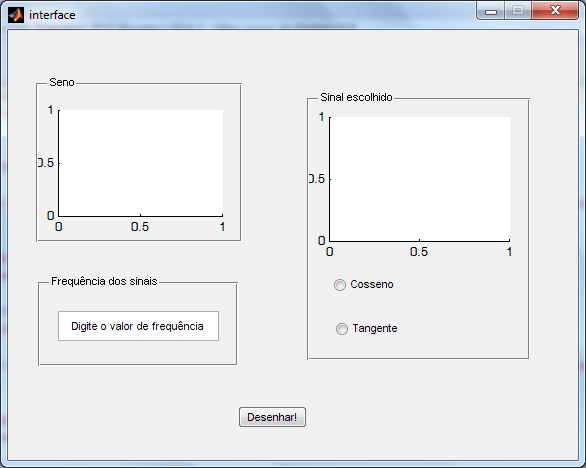
Repare que nenhuma ação é executada ao clicar nos botões ou alterar o campo de texto. Isso acontece porque apenas a interface está criada, falta atribuir ações à cada uma das componentes. É isso que faremos na próxima etapa.
2.2 Atribuir uma ação às componentes
Ao salvar a interface criada, dois arquivos são gerados pela ferramenta, um interface.fig, que é a interface em si, e interface.m que é o código que indica a ação que cada componente gera. Este arquivo é organizado como funções, das quais as mais importantes são:
- interface: Abre a interface criada.
- interface_OpeningFcn: Última função executada antes que a interface seja efetivamente criada. É usada para inicialização de variáveis, etc.
- <componente>_Callback: Ação executada pelo componente ao ser pressionado.
Assim, para atribuir ações aos componentes, basta indicá-las no espaço correspondente à componente. Após escrever o código, não esqueça de salvar o arquivo. A seguir, vamos atribuir algumas ações às componentes:
2.2.1 Ação do botão
Inclua na função pushbutton1_Callback o código:
display('Botão pressionado')
salve, e execute a função. Repare que toda vez que o botão é pressionado, uma mensagem Botão pressionado é impressa na janela de comandos.
2.2.2 Plotando ao pressionar o botão
Para plotar um gráfico ao pressionar o botão, inclua na função pushbutton1_Callback o código:
plot(randn(1,10))
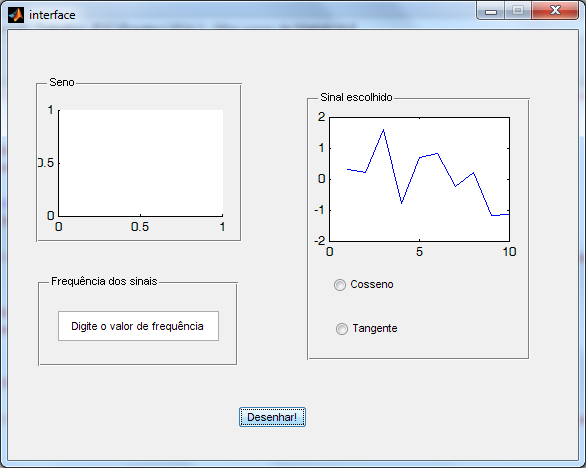
2.2.3 Referenciando uma componente específica
Repare que o eixo em que o gráfico foi plotado não foi escolhido. Para escolher o eixo, é preciso passar para a função plot um indicador da componente a ser utilizada. Todas as componentes estão dispostas na variável handles, struct criada automaticamente pela ferramenta GUIDE. Para esta interface, a variável handles possui os seguintes campos:
handles =
figure1: 191.0381
uipanel3: 27.0389
uipanel2: 25.0389
uipanel1: 19.0397
pushbutton1: 192.0381
radiobutton1: 34.0389
radiobutton2: 33.0389
axes2: 28.0389
edit1: 26.0389
axes1: 20.0389
output: 191.0381
Os valores atribuídos à cada campo não são muito importante, são as referências que o Matlab criou ao gerar a interface. Assim, para escolher o eixo em que o plot será feito, basta passar o valor handles.axes1 ou handles.axes2.
2.2.4 Guardando valores entre componentes
A ação de cada componente é atribuída por uma função dentro do arquivo interface.m. Sendo funções, todas as variáveis criadas são apagadas após sua execução. Caso seja necessário guardar valores entre as ações das componentes, pode-se atribuir à variável handles outros campos, que guardarão os valores desejados.
Por exemplo, para criar um contador de apertos no botão, precisamos de uma variável que guarde o número de vezes que o botão foi pressionado. Criamos um campo chamado contador na variável handles, inicializado com 0, e atribuímos a ação de somar 1 sempre que o botão for pressionado.
Para criar o campo e inicializá-lo com zero, inserimos um código à função interface_OpeningFcn, que ficará assim:
% --- Executes just before interface is made visible. function interface_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to interface (see VARARGIN) handles.contador = 0; %------------------------- Criando o contador % Choose default command line output for interface handles.output = hObject; % Update handles structure guidata(hObject, handles);
O incremento do contador, e a impressão da mensagem com o número de vezes que o botão foi pressionado são incluídos na função pushbutton1_Callback:
handles.contador = handles.contador + 1; display(['O botão foi pressionado ' num2str(handles.contador) ' vezes'])
Porém, ao executar a interface e pressionar o botão, observamos que aparece sempre a mesma mensagem:
>> interface O botão foi pressionado 1 vezes O botão foi pressionado 1 vezes O botão foi pressionado 1 vezes
Isso acontece porque as funções de ação não retornam nenhum valor, ou seja, a alteração realizada na variável handle.contador se perde após a execução da função. Para salvar as variáveis, é necessário usar a função guidata(hObject, handles);. Assim, a função pushbutton1_Callback ficará:
function pushbutton1_Callback(hObject, eventdata, handles) % hObject handle to pushbutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) handles.contador = handles.contador + 1; display(['O botão foi pressionado ' num2str(handles.contador) ' vezes']) guidata(hObject, handles);
Com isso, o problema está resolvido:
>> interface O botão foi pressionado 1 vezes O botão foi pressionado 2 vezes O botão foi pressionado 3 vezes
2.2.5 Capturando o valor do campo de texto
O valor do campo de texto está armazenado na variável hObject, que como o próprio nome já diz, é um objeto. Para atribuir ou receber valores da variável hObject, usamos respectivamente as funções set(hObject,'<atributo>',<valor>) e get(hObject,'<atributo>'). Vimos anteriormente que a variável handles traz a referência para todos os componentes da interface. Em contrapartida, a variável hObject traz os atributos apenas da componente atual, que estamos atribuindo a ação. Cada componente tem seu conjunto de atributos.
Para ver os atributos disponíveis no campo de texto, incluímos na sua função de ação (edit1_Callback) o código get(hObject). Ao alterar o valor do campo, a seguinte mensagem é impressa na janela de comandos:
BackgroundColor = [1 1 1] Callback = [ (1 by 1) function_handle array] CData = [] Enable = on Extent = [0 0 24.8 1.38462] FontAngle = normal FontName = MS Sans Serif FontSize = [8] FontUnits = points FontWeight = normal ForegroundColor = [0 0 0] HorizontalAlignment = center KeyPressFcn = ListboxTop = [1] Max = [1] Min = [0] Position = [3.6 1.76923 32.2 2.30769] String = Valor alterado------------- Style = edit SliderStep = [0.01 0.1] TooltipString = Units = characters Value = [0] BeingDeleted = off ButtonDownFcn = Children = [] Clipping = on CreateFcn = [ (1 by 1) function_handle array] DeleteFcn = BusyAction = queue HandleVisibility = on HitTest = on Interruptible = on Parent = [25.0402] Selected = off SelectionHighlight = on Tag = edit1 Type = uicontrol UIContextMenu = [] UserData = [] Visible = on
Repare que o atributo String recebeu o valor digitado no campo de texto. Assim, é esse o campo que precisamos ler se quisermos receber o valor da frequência digitado pelo usuário. Para guardar o valor digitado, criamos um campo na variável handles.
Criamos o campo f na variável handles e inicializamos com zero, na função interface_OpeningFcn:
function interface_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to interface (see VARARGIN) handles.f = 0; % Choose default command line output for interface handles.output = hObject; % Update handles structure guidata(hObject, handles);
Adicionamos a ação de guardar o valor digitado no campo de texto, na função edit1_Callback. Não esquecer de salvar a alteração na variável com a função guidata(hObject, handles);:
function edit1_Callback(hObject, eventdata, handles) % hObject handle to edit1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) handles.f = get(hObject,'String'); guidata(hObject, handles);
Por fim, configuramos no botão a ação de mostrar na janela de comandos o valor da variável handles.f:
function pushbutton1_Callback(hObject, eventdata, handles) % hObject handle to pushbutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) display(['Valor da variável f: ' handles.f])
Veja as mensagens exibidas, sempre que o botão é pressionado
>> interface Valor da variável f: 4 Valor da variável f: 5 Valor da variável f: ola amiguinhos
2.2.6 Utilizando os radiobuttons
Cada radiobutton tem uma função de ação. O estado de um botão de ação é acessado pelo atributo Value, que se for igual a 1 indica que o botão está marcado e se for igual a 0 indica que o botão não está marcado. Dependendo de vários fatores, ao marcar um botão, é possível que um botão previamente marcado seja desmarcado ou não. Assim, uma ação interessante de ser executada quando um radiobutton for marcado é a desmarcação dos outros radiobuttons. Ou seja, na função de ação do radiobutton1, radiobutton1_Callback, escrevemos:
set(handles.radiobutton1,'Value',1) set(handles.radiobutton2,'Value',0)
E na função de ação do radiobutton2, radiobutton2_Callback, escrevemos:
set(handles.radiobutton1,'Value',0) set(handles.radiobutton2,'Value',1)
Repare que os atributos dos componentes também podem ser acessados a partir da referência disponível na variável handles.
É interessante também guardar o radiobutton escolhido. Para isso, criamos uma variável chamada estado, como um campo da variável handles. Esta variável terá os valores 1 ou 2, dependendo do radiobutton escolhido. Além disso, pode ser necessário inserir um estado inicial dos radiobuttons, evitando que todos fiquem desmarcados. Assim, para trabalhar com os radiobuttons fazemos:
- Adicionamos na função interface_OpeningFcn a criação da variável estado e a rotina de inserção do seu estado inicial:
function interface_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to interface (see VARARGIN) % Diz que o botão selecionado é o 1 handles.estado = 1; % Inicializa o estado dos botões set(handles.radiobutton1,'Value',1) set(handles.radiobutton2,'Value',0) % Choose default command line output for interface handles.output = hObject; % Update handles structure guidata(hObject, handles);
- Dizemos que, ao selecionar um radiobutton o outro deve ser desmarcado, e guardamos o estado dos botões:
function radiobutton1_Callback(hObject, eventdata, handles) % hObject handle to radiobutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Diz que o botão selecionado é o 1 handles.estado = 1; set(handles.radiobutton1,'Value',1) set(handles.radiobutton2,'Value',0) % Update handles structure guidata(hObject, handles);
function radiobutton2_Callback(hObject, eventdata, handles) % hObject handle to radiobutton2 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Diz que o botão selecionado é o 2 handles.estado = 2; set(handles.radiobutton1,'Value',0) set(handles.radiobutton2,'Value',1) % Update handles structure guidata(hObject, handles);
- Inserimos uma função de display como ação do botão:
function pushbutton1_Callback(hObject, eventdata, handles) % hObject handle to pushbutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) display(['Radiobutton selecionado: ' num2str(handles.estado)])
Repare que foi necessário converter o número para string. Ao executar a interface, observamos o resultado esperado:
>> interface Radiobutton selecionado: 1 Radiobutton selecionado: 2 Radiobutton selecionado: 2
2.3 Completando a interface
Para completar a interface, seguimos os passos:
- Na função interface_OpeningFcn, inserimos um estado inicial para os botões, geramos um estado inicial para a frequência dos sinais, geramos o eixo do tempo no qual os sinais estarão definidos e fazemos os plots com os valores padrão:
function interface_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to interface (see VARARGIN) % ------------------------------------------------------ % Diz que o botão selecionado é o 1 handles.estado = 1; % Inicializa o estado dos botões set(handles.radiobutton1,'Value',1) set(handles.radiobutton2,'Value',0) % Inicializa os valores dos sinais handles.f = 0; handles.t = 0:0.001:1; % Faz os plots com os valores padrão plot(handles.axes1,sin(2*pi*handles.f*handles.t)) plot(handles.axes2,cos(2*pi*handles.f*handles.t)) % ------------------------------------------------------ % Choose default command line output for interface handles.output = hObject; % Update handles structure guidata(hObject, handles);
- Na função radiobutton1_Callback, incluímos os códigos para o comportamento adequado:
function radiobutton1_Callback(hObject, eventdata, handles) % hObject handle to radiobutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Diz que o botão selecionado é o 1 handles.estado = 1; set(handles.radiobutton1,'Value',1) set(handles.radiobutton2,'Value',0) % Update handles structure guidata(hObject, handles);
- O mesmo para a função radiobutton2_Callback
function radiobutton2_Callback(hObject, eventdata, handles) % hObject handle to radiobutton2 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Diz que o botão selecionado é o 1 handles.estado = 2; set(handles.radiobutton1,'Value',0) set(handles.radiobutton2,'Value',1) % Update handles structure guidata(hObject, handles);
- Na função edit1_Callback, armazenamos o valor digitado no campo de texto na variável f
function edit1_Callback(hObject, eventdata, handles) % hObject handle to edit1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Pega o valor digitado handles.f = str2double(get(hObject,'String')); % Update handles structure guidata(hObject, handles);
- Por fim, na função pushbutton1_Callback, plotamos o seno com o valor atual de frequência e selecionamos o segundo plot baseados no radiobutton escolhido:
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Faz os plots com os valores padrão
plot(handles.axes1,sin(2*pi*handles.f*handles.t))
if handles.estado == 1
plot(handles.axes2,cos(2*pi*handles.f*handles.t))
elseif handles.estado == 2
plot(handles.axes2,tan(2*pi*handles.f*handles.t))
end
A interface completa está disponível abaixo:
3 Curso Matlab aplicado ao processamento de imagens - Aula 3
O processamento de imagens no Matlab é bastante facilitado. Nesta parte do curso, vamos estudar o básico do processamento de imagens, inicialmente para uma imagem em escala de cinza e depois para uma imagem colorida.
Inicialmente, salve as duas imagens abaixo no diretório de trabalho, e altere o diretório do Matlab para esta pasta. Para facilitar o trabalho, salve as variáveis como imagem1.jpeg e imagem2.jpeg.
- imagem1.jpeg - Imagem de Daniel Teoli Jr, acessível em Link
- imagem2.jpeg - Imagem de Joao Carlos Medau, acessível em Link
3.1 Imagem em escala de cinza
Para ler uma imagem do computador, é utilizada a função imread:
>> x = imread('imagem1.jpeg');
Para visualizar a imagem, é utilizada a função imshow. Uma figura pode antes ser aberta, para evitar que a imagem seja exibida em cima de uma outra figura:
>> figure >> imshow(x)
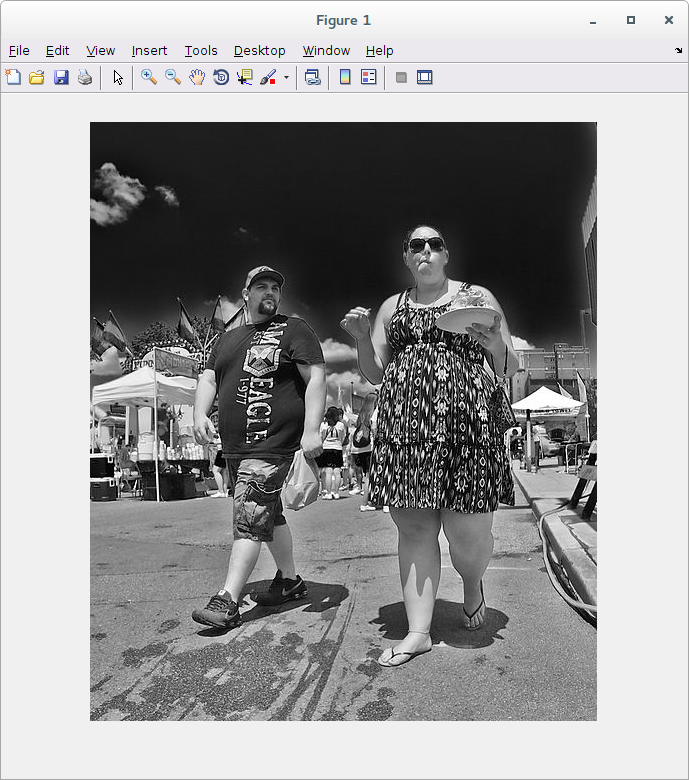
Pelo comando whos, é possível perceber alguns atributos da imagem:
>> whos x Name Size Bytes Class Attributes x 599x507 303693 uint8
A imagem é para o Matlab uma matriz de 599x507, do tipo uint8. Sendo o valor um inteiro de 8 bits sem sinal, os valores podem ir de 0 a 255. No Matlab, valores mais próximos de 0 são de cor escura e valores mais próximos de 1 são de cor clara.
3.1.1 Negativo da imagem
Para tirar o negativo da imagem, precisamos transformar valores próximos de 0 em valores próximos de 255, e vice-versa. Uma forma de fazer isso é subtrair 255 da imagem, e depois multiplicar por -1. Neste caso, porém, precisaremos realizar uma mudança no tipo do dado, pois a variável é inteira e sem sinal:
>> y = uint8(-1*(double(x)-255)); >> figure >> imshow(y)
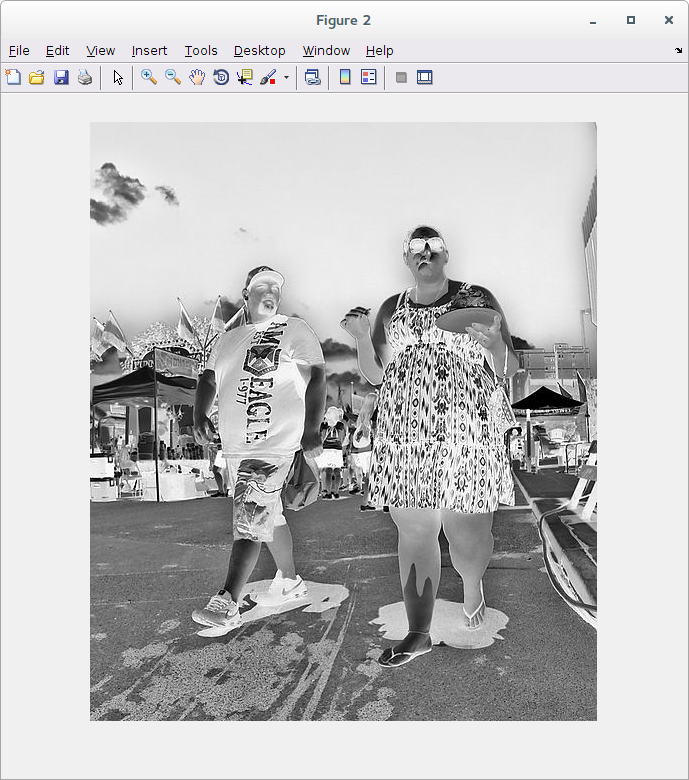
3.1.2 Aumentando e reduzindo o brilho
Aumentar o brilho significa deixar a imagem mais clara. Esta operação é feita somando uma constante à imagem:
>> z = x + 50; >> figure >> imshow(z)
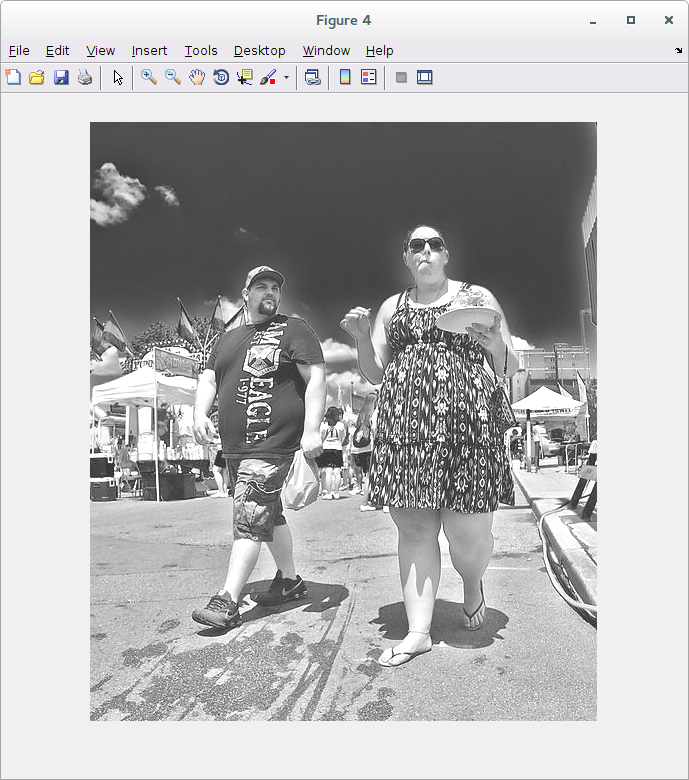
3.1.3 Aumentando e reduzindo o contraste
Para aumentar o contraste, deixamos as cores claras mais claras e as cores escuras mais escuras. Isso pode ser feito facilmente no Matlab com algumas operações matemáticas. Primeiro, definimos o que são cores claras e o que são cores escuras, através de um limiar:
>> limiar = 180;
Esta variável indica que todos os valores com intensidade acima de 180 serão realçados enquanto todos abaixo de 180 serão atenuados. Com o limiar definido, fazemos uma operação de divisão:
>> a = double(x)/limiar;
O resultado da divisão será:
- Números entre 0 e 1, para valores de x menores que 180
- Números maiores que 1, para valores maiores que 180
Por isso a conversão de x para o tipo double foi necessária, já que o tipo uint8 não permite representar esses resultados. Após a divisão, o aumento no contraste é realizado por uma potenciação:
>> b = a.^2;
Essa operação faz com que os valores maiores que 1 fiquem ainda maiores, e os valores menores que 1 ainda menores. A operação é concluída ao multiplicar os valores pelo limiar, e converter os dados para uint8 novamente:
>> c = uint8(b*limiar);
Para observar o resultado, mostramos uma imagem ao lado da outra:
>> figure
>> subplot(1,2,1); imshow(x); title('Imagem original')
>> subplot(1,2,2); imshow(c); title('Imagem com o contraste aumentado')

O contraste pode ser ainda mais realçado ao utilizar potências maiores do que 2. Da mesma forma, podemos reduzir o contraste ao utilizar operações de raiz.
3.1.4 Binarização
A binarização é uma forma de separar regiões de imagens. A imagem resultante será branca nas regiões onde a intensidade da imagem original é maior que um determinado limiar e preta nas outras regiões. Essa operação é realizada de forma muito simples no Matlab. Para demonstrar isso, vamos usar o mesmo limiar utilizado no aumento de contraste. A binarização é realizada a partir de um teste:
>> d = x >= limiar;
Na linha acima, primeiro testamos se x é maior ou igual ao limiar. O Matlab retorna o lógico 1 quando o teste é verdadeiro e o lógico 0 quando o teste é falso. Esses resultados são armazenados na variável d.
Ao analisar o resultado (o imshow entende quando seu argumento é uma matriz binária), vemos que as partes mais claras da imagem ficaram brancas, enquanto as mais escuras ficaram pretas.

3.1.5 Adicionando uma marca d'água
Marcas d'água são pequenos logos incluídos nas imagens, normalmente utilizados para informação de autoria. Vamos adicionar o logo do IFSC na imagem em escala de cinza x que estamos utilizando até agora.
Primeiro, baixamos o logo do IFSC e salvamos na mesma pasta que estamos trabalhando, com o nome logo.gif. Lemos o arquivo no Matlab com:
>> marca = imread('logo.gif');
Para adicionar o logo como marca d'água, vamos transformar seus valores de forma que os seus valores máximos (cores brancas) fiquem com um valor 1. Para isso, executamos:
>> marca = double(marca)/double(max(max(marca)));
Assim, o valor máximo da imagem será dividido por ele mesmo, o que resultará em 1. Os outros valores ficarão entre 0 e 1.
Para poder multiplicar o logo pela imagem, precisamos corrigir a diferença no tamanho entre as matrizes. Para isso, vamos criar uma nova matriz, de nome camada, do mesmo tamanho da imagem. A matriz será composta de 1.
>> camada = ones(size(x));
Após isso, localizamos o logo dentro da camada, via indexação:
>> camada(1:size(marca,1), 1:size(marca,2)) = marca;
Assim, estamos dizendo que o logo ficará distribuído na matriz camada a partir da linha e coluna 1:

Após isso, basta realizar a multiplicação ponto a ponto das imagens, não esquecendo as conversões necessárias:
>> e = uint8(double(x) .* camada);
Como resultado, temos a imagem original com a marca do IFSC incluída na parte superior esquerda:

3.1.6 Suavização
Suavizar uma imagem significa reduzir sua nitidez. É realizado através do cálculo da média local ao redor de todos os pixels da imagem. No Matlab, isso é feito com a criação de uma matriz de média, chamada de máscara para realização de uma operação de convolução.
- Primeiro, uma matriz de média é criada. Ela deve ser quadrada, de tamanho ímpar, e a soma de seus elementos deve resultar em 1:
>> mask1 = (1/9)*[1 1 1; 1 1 1; 1 1 1]
mask1 =
0.1111 0.1111 0.1111
0.1111 0.1111 0.1111
0.1111 0.1111 0.1111
>> sum(sum(mask1))
ans =
1
- O cálculo da média é efetivado com o uso da função conv2. Essa função percorre a máscara por todos os pixels da imagem, realizando operações de multiplicação e soma.
>> suav1 = conv2(x,mask1);
- A imagem resultante tem porém, 1 pixel a mais em cada borda:
>> whos x suav1 Name Size Bytes Class Attributes suav1 601x509 2447272 double x 599x507 303693 uint8
- Assim, descartamos esses pixels:
>> suav1 = suav1(2:end-1, 2:end-1); >> size(suav1) ans = 599 507
- Para ver os resultados, exibimos as imagens lado a lado:
>> figure >> subplot(1,2,1); imshow(x) >> subplot(1,2,2); imshow(uint8(suav1))

Outros tipos de operadores de média podem ser utilizados, com máscaras maiores, ou mesmo não uniformes. Para máscaras uniformes, a função ones pode ser utilizada:
>> mask2 = (1/25)*ones(5,5)
mask2 =
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
0.0400 0.0400 0.0400 0.0400 0.0400
>> mask3 = (1/15)*[1 2 1; 2 3 2; 1 2 1]
mask3 =
0.0667 0.1333 0.0667
0.1333 0.2000 0.1333
0.0667 0.1333 0.0667
3.1.7 Detecção de bordas
A detecção de bordas em imagens é feita de forma semelhante à suavização, porém uma máscara diferente é utilizada. Neste curso vamos usar uma máscara específica, de Sobel, mas existem muitas outras que podem ser utilizadas, com vantagens e desvantagens específicas. A máscara de Sobel é definida para bordas verticais e horizontais, respectivamente:
>> sobel_v = [-1, -2, -1; 0, 0, 0; 1, 2, 1]
sobel_v =
-1 -2 -1
0 0 0
1 2 1
>> sobel_h = [-1, 0, 1; -2, 0, 2; -1, 0, 1]
sobel_h =
-1 0 1
-2 0 2
-1 0 1
Ao aplicar os operadores na imagem, usando a função conv2, temos como resultado as imagens abaixo:
>> borda_v = conv2(x,sobel_v);
>> borda_h = conv2(x,sobel_h);
>> borda_v = borda_v(2:end-1,2:end-1);
>> borda_h = borda_h(2:end-1,2:end-1);
>> figure
>> subplot(1,2,1); imshow(uint8(borda_v)); title('Bordas verticais da imagem')
>> subplot(1,2,2); imshow(uint8(borda_h)); title('Bordas horizontais da imagem')

Pode também ser feita a soma das componentes verticais e horizontais das bordas:
>> borda = borda_v + borda_h;
>> figure
>> subplot(1,2,1); imshow(x); title('Imagem original')
>> subplot(1,2,2); imshow(uint8(borda)); title('Bordas da imagem')

3.2 Imagem colorida
Agora vamos ler a imagem colorida, e verificar as diferenças com relação à escala de cinza:
>> a = imread('imagem2.jpeg');
>> figure
>> imshow(a)

Ao executar o comando whos, percebemos as diferenças entre as imagens:
>> whos a Name Size Bytes Class Attributes a 388x640x3 744960 uint8
Repare que, da mesma forma que a imagem em escala de cinza, a imagem colorida é composta por valores do tipo uint8. Porém, neste caso, há uma terceira dimensão disponível. É a partir desta nova dimensão que as características de cor são passadas. Uma imagem colorida é composta por 3 planos de cor, cada um representando a quantidade disponível das cores vermelho, verde ou azul. Quanto maior o valor de um elemento do plano, maior a quantidade da cor correspondente. Com isso, temos as componentes RGB da imagem.
3.2.1 Criando uma imagem da paleta de cores
Vamos criar uma imagem que indica a quantidade de cada cor disponível. Para isso, vamos separar uma figura do Matlab em 4 sub-figuras com a função subplot. Primeiro, abrimos uma nova figura, e na primeira subfigura, exibimos a imagem colorida:
>> figure
>> subplot(2,2,1); imshow(a); title('Imagem colorida')
Na segunda sub-figura, plotamos as componentes de vermelho:
>> subplot(2,2,2); imshow(a(:,:,1)); title('Componentes de vermelho - R')
Na terceira, os componentes de verde:
>> subplot(2,2,3); imshow(a(:,:,2)); title('Componentes de verde - G')
Na quarta, os componentes de azul:
>> subplot(2,2,4); imshow(a(:,:,3)); title('Componentes de azul - B')
Repare nas diferenças entre as 3 figuras de cor:

3.2.2 Paleta de cores modificada
Visando deixar a imagem da paleta de cores um pouco mais visual, vamos criar imagens baseadas na imagem inicial. Criamos 3 matrizes, b_R, b_G, e b_B, do tamanho da imagem inicial, inicialmente com zeros. Não esquecer que o tipo dos dados deve ser uint8.
>> b_R = uint8(zeros(size(a))); >> b_G = uint8(zeros(size(a))); >> b_B = uint8(zeros(size(a)));
Após isso, atribuímos o primeiro plano da imagem original ao primeiro plano da imagem b_R. O segundo plano da imagem original é atribuído ao segundo plano da imagem b_G, e o terceiro plano ao terceiro plano da imagem b_B:
>> b_R(:,:,1) = a(:,:,1); >> b_G(:,:,2) = a(:,:,2); >> b_B(:,:,3) = a(:,:,3);
Feito isso, realizamos os subplots da mesma forma como antes:
>> figure
>> subplot(2,2,1); imshow(a); title('Imagem colorida')
>> subplot(2,2,2); imshow(b_R); title('Componentes de vermelho - R')
>> subplot(2,2,3); imshow(b_G); title('Componentes de verde - G')
>> subplot(2,2,4); imshow(b_B); title('Componentes de azul - B')
Com essa nova imagem, deixamos ainda mais claro como estão distribuídas as componentes de cor.

3.3 Projeto final
O projeto consiste na criacao de uma ferramenta de processamento de imagens. O usuario ira entrar com o nome do arquivo num campo de texto, e clicar num botao para a realizacao da leitura da imagem. A imagem sera lida pelo sistema e exibida no eixo da imagem original. Na segunda area da interface, varias operacoes poderao ser selecionadas, e os resultados serao exibidos no eixo da imagem processada.