ANC60805 2015-2

CÓDIGO DA UNIDADE CURRICULAR - ANC60805

PROFESSORES: Bruno Fontana da Silva (até 16/12/2015) // ???

CONTATO: bruno.fontana@ifsc.edu.br / ???

SEMESTRE: 2015 - 2

ENCONTROS: Terça-feira (07h30min) e Quinta-feira (07h30min)

Bem vindo ao Diário de Aulas de Análise de Circuitos II (ANC60805).

1 Turmas A/B para Aulas Práticas

2 Avaliações

• Avaliação 01 (12/11/2015)

Obs.: na questão 2, do item (b) em diante, usar $R1=R2=100\mathrm{\Omega }$ e $C=10\mu F$.

Refazer a avaliação e entregar a solução na aula do dia 19 de Novembro, às 7h30min..

• Notas Finais da Avaliação 01

• Avaliação 02 (17/12/2015)
• Avaliação 02 (versão 2) (21/12/2015)

• Notas Finais da Avaliação 02

2.1 Notas Parciais: 2015/2

• Notas Parciais 2015-2

Recuperações: ocorrerão em Fevereiro de 2016/1, a combinar com o próximo professor responsável pela disciplina.

Estudar as listas de exercício da Wiki (de 01b a 05b) de acordo com os conteúdos que precisam ser recuperados.

3 Cronograma das Atividades

4 Notas de Aula

4.1 Aula 01 (06/10)

Aula 01 (06/10) - Revisão de Circuitos DC e Análise Transitória RC/RL

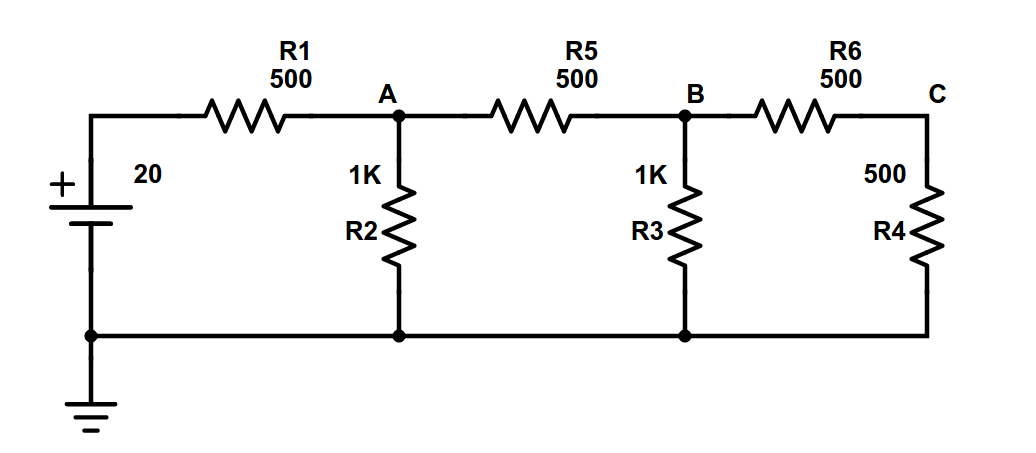
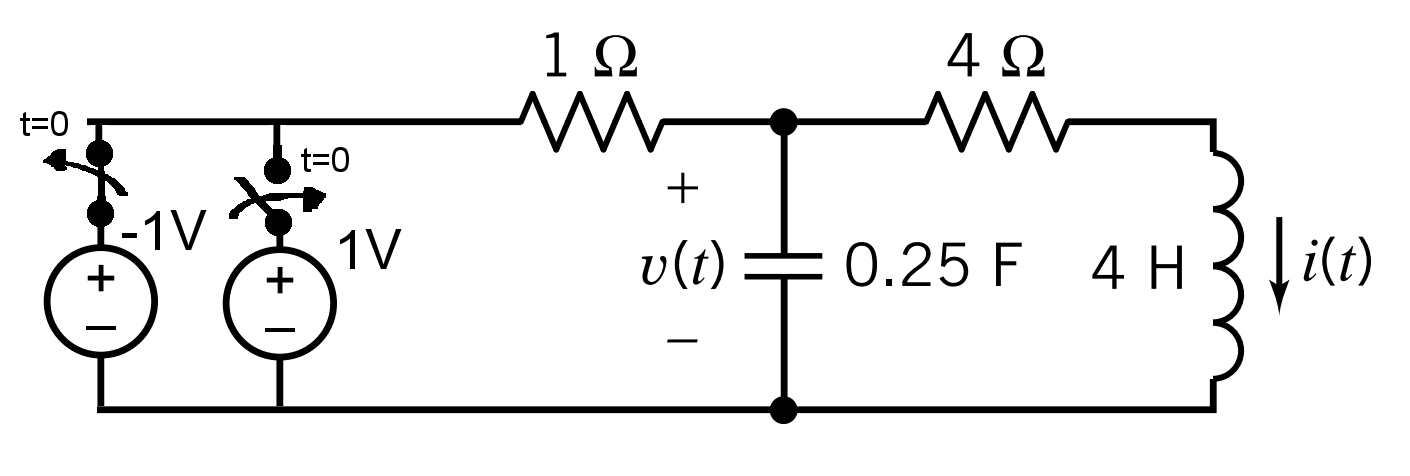
Figura 1: Cascata de divisores resistivos. Figura 2: Circuito RC. Figura 2: Circuito RC. Simulador On-line (PartSim da DigiKey) Simulador LTspice IV (Linear Technology) Atividades de aula No circuito da Figura 1: encontrar os valores de tensão A, B e C; encontrar as correntes e potências em todos os resisotores; tarefa de casa: simular o ponto de operação DC do circuito e validar os valores calculados em sala. No circuito da Figura 2, assumindo que a tensão inicial do capacitor é V(C1) = 0 Volts (capacitor descarregado), calcule: os valores de tensão e corrente iniciais dos componentes R1 e C1; os valores de tensão e correntes dos componentes R1 e C1 em regime permanente; a constante de tempo do circuito $({\tau }_{RC}=R\times C)$; o tempo de carga do capacitor $(t_{charge}\approx 5{\tau }_{RC})$; tarefa de casa: simular a curva transiente de carga do capacitor (corrente e tensão). No circuito da Figura 3, assumindo que a tensão corrente inicial do indutor é $i(L1)=0$ Ampéres (indutor descarregado), calcule: os valores de tensão e corrente iniciais dos componentes R2 e L1; os valores de tensão e correntes dos componentes R2 e L1 em regime permanente; a constante de tempo do circuito $({\tau }_{RL}=\frac{L}{R})$; o tempo de carga do capacitor $(t_{charge}\approx 5{\tau }_{RL})$; tarefa de casa: simular a curva transiente de carga do indutor (corrente e tensão).

4.2 Aula 03 (13/10)

Aula 03 (13/10) - Revisão de Funções Trigonométricas

Aula com Revisão de Funções Trigonométricas Exemplo: Para um sinal de tensão com a seguinte forma de onda: $v_1(t)=20\cos (2\pi 1000t+\frac{\pi }{3})+2$ defina: o valor de amplitude do sinal; a frequência angular; a frequência em ciclos por segundo (Hz); o período do sinal; a fase do sinal; a componente DC do sinal; $v(t=1ms)$. Solução Observe que os sinais baseados em funções trigonométricas sempre seguem o formato: $f(t)=A\cos (\omega t+\varphi )+\text{offset}$, sendo $A$ o valor de amplitude do sinal; $\omega =2\pi f$ a frequência angular, em que $f$ é a frequência em Hz; $\varphi$ a fase inicial do sinal alternado; $\text{offset}$ um valor constante correspondente à média (ou valor DC) do sinal. Igualando as duas expressões, $f(t)=v_1(t)$ $A\cos (\omega t+\varphi )+\text{offset}=20\cos (2\pi 1000t+\frac{\pi }{3})+2$ observamos, por inspeção, que $A=20$ $\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{s}$ (corresponde ao valor que multiplica o cosseno); $\omega =2000\pi$ $\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$ (corresponde ao coeficiente que multiplica a variável $t$ do tempo) $\varphi =\frac{\pi }{3}$ $\mathrm{r}\mathrm{a}\mathrm{d}$ (corresponde ao ângulo constante no argumento do cosseno, ou seja, livre da variável $t$) $\text{offset}=2$ $\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{s}$ (corresponde ao valor constante da função, eliminando os termos cossenoidais). A frequência em Hertz é encontrada através da frequência angular: $\omega =2\pi f$ $f=\frac{\omega }{2\pi }$ $f=\frac{2000\pi }{2\pi }=1000$ $\mathrm{H}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{z}$ (ou ciclos por segundo). O período do sinal (tempo de duração de um ciclo) é o inverso da frequência: $T=\frac{1}{f}$ $T=1$ $\mathrm{m}\mathrm{s}$. Por fim, para encontrar $v(t=1\mathrm{m}\mathrm{s})$ basta substituir $t=1\mathrm{m}\mathrm{s}$ na equação de $v(t)$.. $v(t=1\mathrm{m}\mathrm{s})=20\cos (2\pi 1000\times 1\times 10^{-3}+\frac{\pi }{3})+2$ $v(t=1\mathrm{m}\mathrm{s})=20\cos (2\pi +\frac{\pi }{3})+2$ $v(t=1\mathrm{m}\mathrm{s})=20\cos \left(\frac{\pi }{3}\right)+2$ $v(t=1\mathrm{m}\mathrm{s})=20\times \frac{1}{2}+2$ $v(t=1\mathrm{m}\mathrm{s})=12$ $\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{s}$.

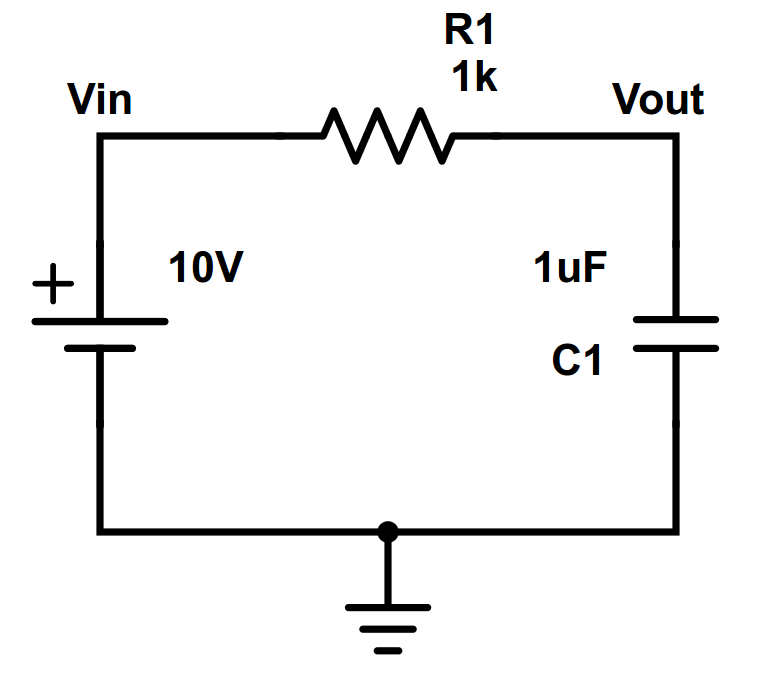
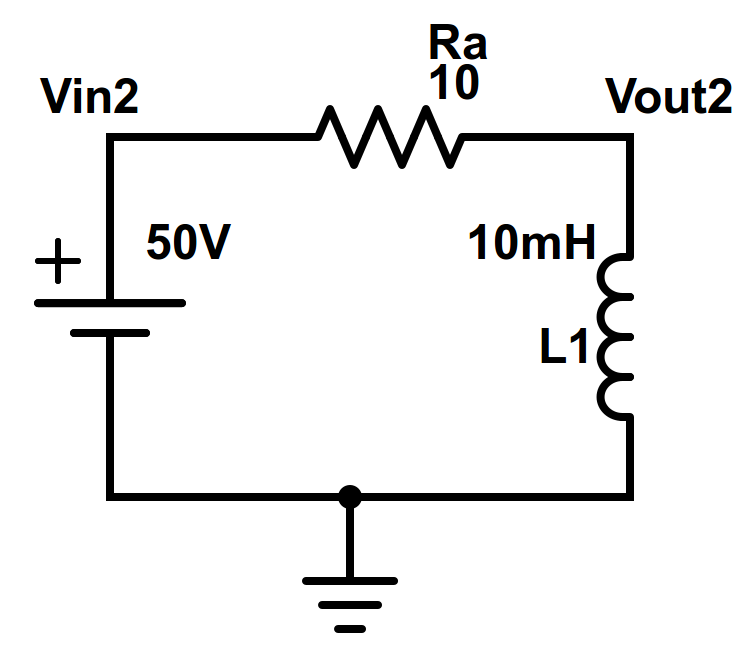
4.3 Aula 04 (15/10)

Aula 04 (15/10) - Revisão de Números Complexos

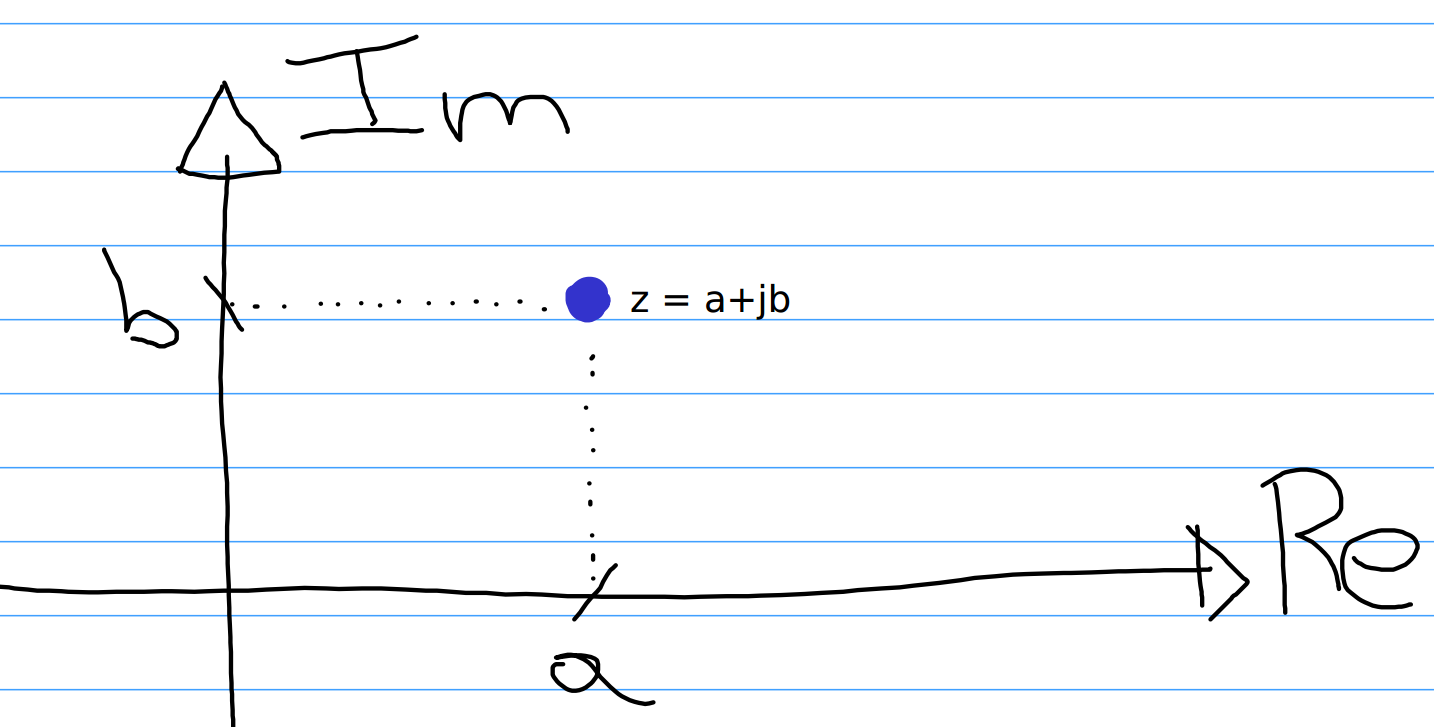
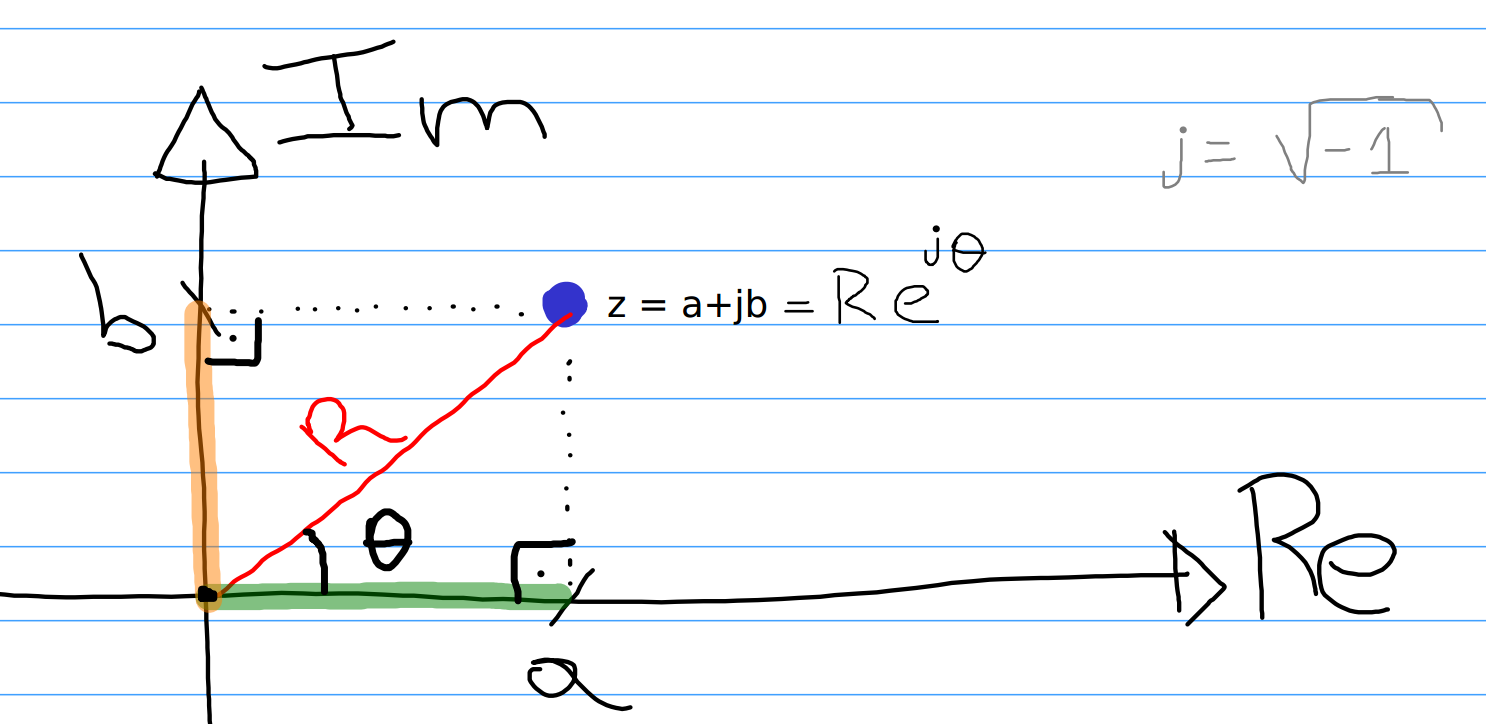
Figura 1: Representação gráfica do número complexo z no Plano Complexo. Figura 2: Representação gráfica do número complexo z no Plano Complexo. 4.3.1 Forma Retangular Seja a unidade imaginária definida como $j\triangleq \sqrt{-1}$. A forma retangular de um número complexo $z$ é dada como: $z=a+jb$, sendo $a=\mathrm{\Re }\{z\}$ a parte real do número complexo $z$ e $b=\mathrm{\Im }\{z\}$ a parte imaginária do número complexo $z$. A representação do número complexo $z$ pode ser realizada graficamente através do Plano Complexo (observe a Figura 1). 4.3.2 Forma Polar O número complexo $z$ também pode ser representado na forma polar, através de um módulo ($R$ ) e um ângulo ($\theta$ ). Observe as relações em destaque na Figura 2. $\begin{array}{rl}a& =R\cos \left(\theta \right)\\ b& =R\sin \left(\theta \right)\\ \\ z& =a+jb\\ & =R\cos \left(\theta \right)+jR\sin \left(\theta \right)\\ & =R(\cos \left(\theta \right)+j\sin \left(\theta \right))\end{array}$ Observando a geometria da Figura 2, também é possível concluir que: $\begin{array}{rl}R& =\sqrt{a^2+b^2}\\ \theta & ={\tan }^{-1}\left(\frac{b}{a}\right)\end{array}$ 4.3.3 Equação de Euler A fórmula de Euler é uma fórmula matemática na análise de números complexos que estabelece uma relação entre funções trigonométricas e funções exponenciais complexas. 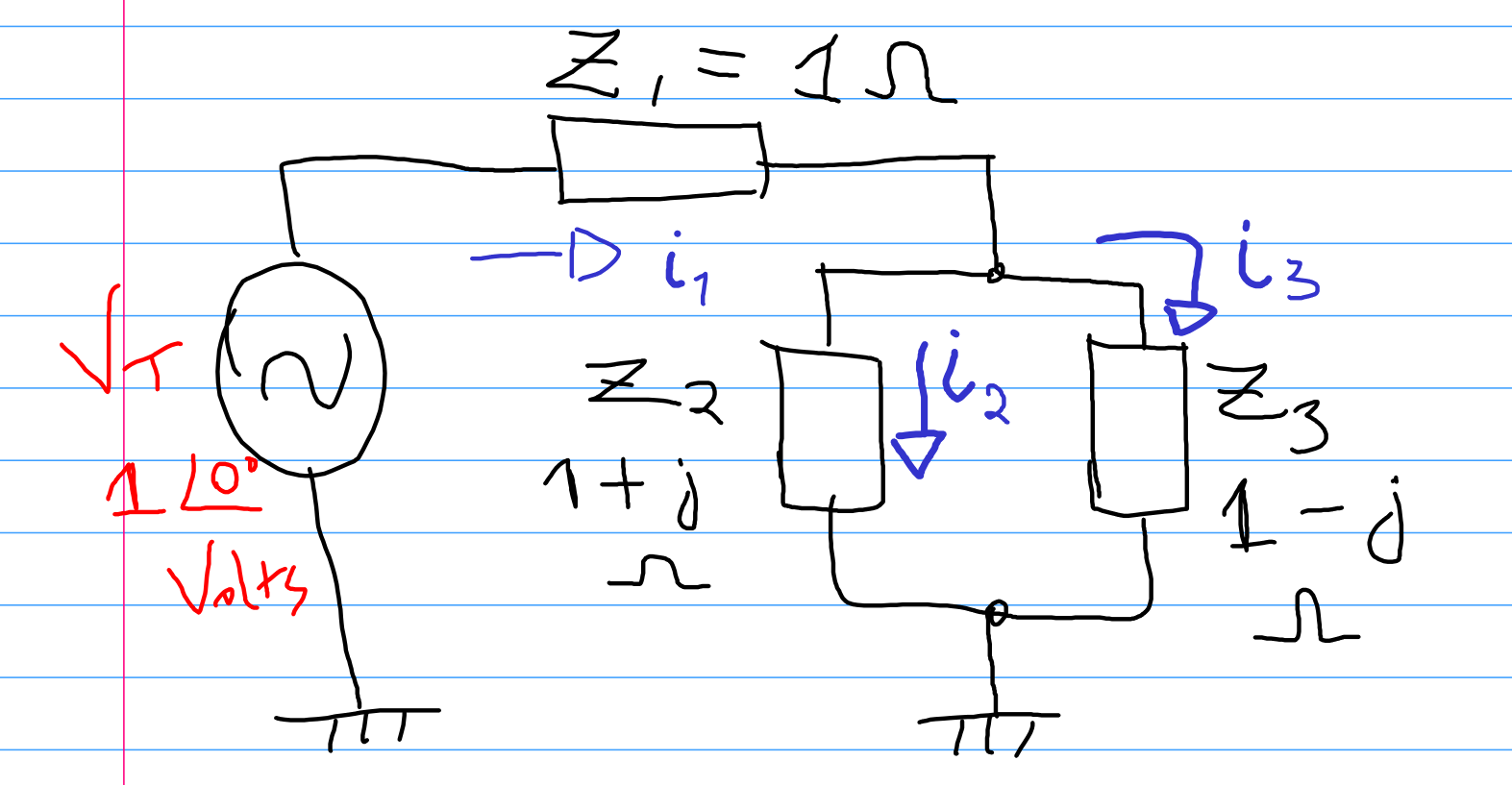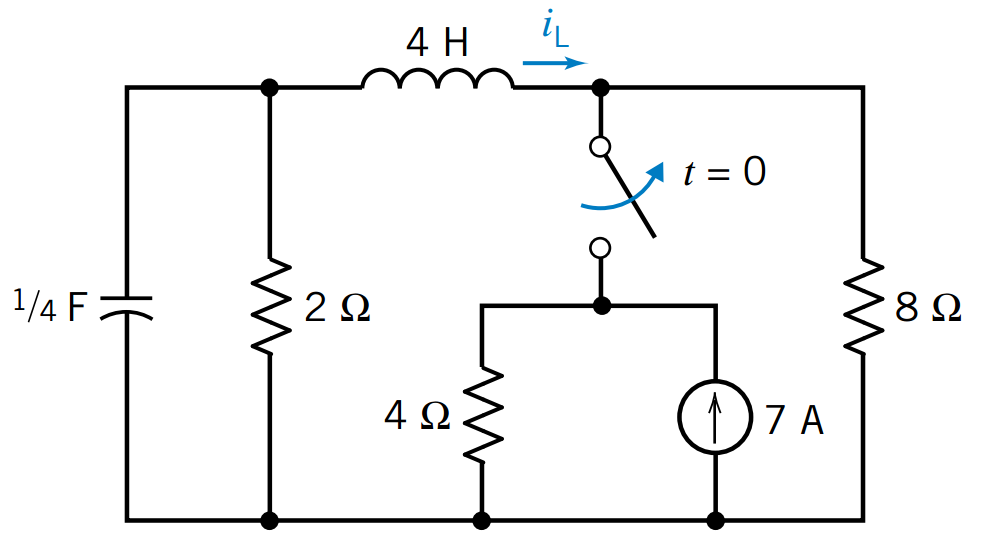$\begin{array}{rl}{e}^{j\theta }& =\cos \left(\theta \right)+j\sin \left(\theta \right)\end{array}$ Através dessa relação e das formas polar e retangular apresentadas anteriormente para o número complexo $z$ , concluímos que: $\begin{array}{rl}z& =a+jb\\ & =R{e}^{j\theta }\end{array}$ 4.3.4 Conjugado de um número complexo $\overline{z}=a-jb=R{e}^{-j\theta }$ 4.3.5 Exemplos (1) Considere o circuito da Figura 3 e calcule a tensão e a corrente em todos os elementos do circuito. Solução $\begin{array}{rl}{Z}_T& =Z_1+Z_2//Z_3\\ & =Z_1+\frac{Z_2\times Z_3}{Z_2+Z_3}\end{array}$ $\begin{array}{rl}{i}_1& =\frac{V_T}{Z_T}\end{array}$ $\begin{array}{rl}{V}_1& =i_1\times Z_1\end{array}$ $\begin{array}{rl}{V}_2& =V_3=V_T-V_1\end{array}$ $\begin{array}{rl}{i}_2& =\frac{V_2}{Z_2}\end{array}$ $\begin{array}{rl}{i}_3& =\frac{V_3}{Z_2}\end{array}$ Figura 3: Representação de um circuito AC com impedâncias.

4.4 Aula 05 (19/10)

Aula 05 (19/10) - Fontes Senoidais
Exemplo 1: configurando tempo total e passo de simulação. Exemplo 2: configurando tempo total e passo de simulação. Circuito resistivo com fonte senoidal Expressão cossenoidal a partir do gráfico simulado

4.5 Aulas 06 e 07 (22/10 e 27/10)

Aulas 06 e 07 (22/10 e 27/10) - Impedância Complexa e Diagrama Fasorial

Em regime permanente senoidal (RPS) de corrente alternada (CA), o efeito de carga e descarga dos elementos armazenadores de energia pode ser representado utilizando números complexos. A frequência angular das fontes CA é representada pela variável $\omega =2\pi f$ $(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s})$, sendo $f$ o valor da frequência da fonte em Hertz. Definimos o conceito de impedância como sendo a dificuldade à passagem da corrente oferecida por um elemento capacitor ou indutor quando sujeito à uma entrada de energia senoidal. 4.5.1 Impedância do capacitor Para o capacitor, a impedância é dada por: $Z_C=-j{X}_C=\frac{1}{j\omega C}$, sendo $\begin{array}{rl}& X_C=\frac{1}{\omega C}\end{array}$ denominada a reatância do capacitor (módulo de sua impedância). A fase da impedância do capacitor é $-\frac{\pi }{2}$ ou $-90^{\circ }$. 4.5.2 Impedância do Indutor = Para o indutor, a impedância é dada por: $\begin{array}{rl}{Z}_L& =j{X}_L\\ & =j\omega L\end{array}$, sendo $\begin{array}{rl}& X_L=\omega L\end{array}$ denominada a reatância do indutor (módulo de sua impedância). A fase da impedância do indutor é $\frac{\pi }{2}$ ou $90^{\circ }$. 4.5.3 Associações de Impedâncias A associação de impedâncias é idêntica à associação de resistores. Sejam $\begin{array}{rl}& Z_1\end{array}$ e $\begin{array}{rl}& Z_2\end{array}$ duas impedâncias quaisquer. Ao conectar os terminais de $\begin{array}{rl}& Z_1\end{array}$ e $\begin{array}{rl}& Z_2\end{array}$ em paralelo, a impedância equivalente fica: $\begin{array}{rl}{Z}_p& =\frac{Z_1\times Z_2}{Z_1+Z_2}\end{array}$. Na associação em série de $\begin{array}{rl}& Z_1\end{array}$ e $\begin{array}{rl}& Z_2\end{array}$, o equivalente fica: $\begin{array}{rl}{Z}_s& =Z_1+Z_2\end{array}$. 4.5.4 Exemplos Solução

4.6 Aula 08

Aula 08 - Função de Transferência

4.7 Aula 09 (14/11/15)

Aula 09 - Teorema da Superposição em Circuitos AC

Teorema da Superposição Para aplicação do teorema da superposição, vamos considerar que: o circuito é formado exclusivamente por elementos passivos lineares (resistores, capacitores e indutores) e fontes dependentes e independentes; as entradas do circuito são as tensões de todas as fontes de tensão independentes e as correntes de todas as fontes de corrente independentes; a saída é a tensão ou a corrente de qualquer componente do circuito. O teorema da superposição afirma que a saída de um circuito linear produzida por várias entradas agindo simultaneamente é igual à soma das saídas produzidas pelas entradas agindo separadamente. $\begin{array}{r}(\genfrac{}{}{0ex}{}{\mathrm{\#}\text{ de circuitos}}{\text{a serem analisados}})=(\genfrac{}{}{0ex}{}{\mathrm{\#}\text{ de fontes}}{\text{independentes}})\end{array}$ Passos para aplicar o teorema da superposição: (1) Escolha uma fonte para manter no circuito e calcular o efeito que ela produz no circuito separadamente. (2) Para o resto das fontes, torne a sua influência nula da seguinte forma: (a) ao remover uma fonte de tensão, substitua-a por uma conexão direta de resistência nula (curto-circuito); (b) ao remover uma fonte de corrente, substituta-a por um circuito aberto (resistência infinita). (3) Determine as correntes de malha ou tensões dos nós produzidas pela fonte do passo (1). (4) Repita o procedimento de (1) a (3) com as demais fontes do circuito que ainda não foram analisadas. (5) ***Some algebricamente os efeitos das correntes de malha (ou tensões dos nós) de todas as fontes. Ou seja, a corrente (ou tensão) através de qualquer elemento é igual à soma algébrica das correntes (ou tensões) produzidas independentemente pro cada fonte. Caso 1: Fontes CA de mesma frequência $\begin{array}{r}\omega \end{array}$ Aplicar o procedimento de forma direta. O efeito total pode ser combinado diretamente na forma polar (fontes CA). $\begin{array}{r}{V}_{T,\omega }=V_1\mathrm{\angle }{\theta }_1+V_2\mathrm{\angle }{\theta }_2+\dots +V_N\mathrm{\angle }{\theta }_N\end{array}$ $\begin{array}{r}{i}_{T,\omega }=i_1\mathrm{\angle }{\varphi }_1+i_2\mathrm{\angle }{\varphi }_2+\dots +i_N\mathrm{\angle }{\varphi }_N\end{array}$ Caso 2: Fontes de frequências diferentes ***Neste caso, o passo (5) deve ser realizado no domínio do tempo e NÃO pode ser realizado na forma polar. Ou seja, para obter o resultado final, devem-se somar as funções trigonométricas das correntes (ou tensões) que foram calculadas separadamente. $\begin{array}{r}{V}_{T,CA}(t)=V_1\cos ({\omega }_{1}t+{\theta }_1)+V_2\cos ({\omega }_{2}t+{\theta }_2)+\dots +V_N\cos ({\omega }_{N}t+{\theta }_N)\end{array}$ $\begin{array}{r}{i}_{T,CA}(t)=i_1\cos ({\omega }_{1}t+{\varphi }_1)+i_2\cos ({\omega }_{2}t+{\varphi }_2)+\dots +i_N\cos ({\omega }_{N}t+{\varphi }_N)\end{array}$ Caso 3: Fonte CC e Fonte CA ***Neste caso, o passo (5) deve ser realizado no domínio do tempo e NÃO pode ser realizado na forma polar. O resultado final é obtido somando as funções trigonométricas das correntes (ou tensões) alternadas que foram calculadas separadamente com as correntes (ou tensões) de corrente contínua resultantes. $\begin{array}{r}{V}_T(t)=V_{T,CC}+V_{T,CA}(t)\end{array}$ $\begin{array}{r}{i}_T(t)=i_{T,CC}+i_{T,CA}(t)\end{array}$

4.8 Aulas 10 e 11 (17/11/2015 e 19/11/2015)

Aulas 10 e 11 - Potência em Circuitos CA

Potência instantânea Como a tensão e a corrente variam no tempo em circuitos com fontes alternadas, a potência também é variante no tempo. A potência instantânea em qualquer elemento de um circuito é definida como o produto dos sinais instantâneos de tensão e corrente nesse elemento: $\begin{array}{rl}p(t)& =v(t)i(t)[\mathrm{W},\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{s}]\end{array}$. No arquivo abaixo, você pode analisar a interpretação de potência instantânea de fontes senoidais em um circuito RLC, alterando valores como frequência, capacitância, indutância e resistência para observar os efeitos em termos de potência instantânea da fonte. Análise da Potência Instantânea em Circuito CA Circuito RLC Série Valores Eficazes Para comparar a potência efetiva de um circuito de corrente alternada com um circuito de corrente contínua, define-se o conceito de valor eficaz (RMS) de um sinal periódico $\begin{array}{r}x(t)\end{array}$ como sendo: $\begin{array}{r}{x}_{RMS}=\sqrt{\frac{\text{area de }{x}^2(t)}{\text{periodo de }x(t)}}\end{array}$ sendo a área de $\begin{array}{r}{x}^2(t)\end{array}$ calculada apenas dentro de um período de $\begin{array}{r}x(t)\end{array}$ $\begin{array}{r}[0,T]\end{array}$. Para sinais periódicos (cos)senoidais de valor médio nulo, tem-se que o valor RMS é aproximadamente 70,7% do valor de pico, dado pela fórmula: $\begin{array}{r}{x}_{RMS}=\frac{x_{pico}}{\sqrt{2}}\end{array}$. Potência Complexa A potência aparente, na forma complexa polar, é dada por: $\begin{array}{rl}S& =\frac{V_{pico}{\overline{i}}_{pico}}{2}\\ & =|V_{rms}||i_{rms}|\mathrm{\angle }({\theta }_V-{\theta }_i)[\mathrm{V}\mathrm{A},\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{\cdot }\mathrm{A}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}]\\ & =P+jQ\end{array}$ sendo que: $\begin{array}{r}|V_{rms}|=\frac{|V_{pico}|}{\sqrt{2}}\end{array}$ é o valor eficaz da tensão; $\begin{array}{r}|i_{rms}|=\frac{|i_{pico}|}{\sqrt{2}}\end{array}$ é o valor eficaz da corrente; $\begin{array}{r}{\theta }_V\end{array}$ é o ângulo da tensão (na forma polar); $\begin{array}{r}{\theta }_i\end{array}$ é o ângulo da corrente (na forma polar); $\begin{array}{r}{\overline{i}}_{pico}\end{array}$ é o valor complexo conjugado corrente de pico. Na forma retangular de $\begin{array}{rl}S& =P+jQ\end{array}$ podemos identificar dois termos, denominados potência ativa ($\begin{array}{r}P\end{array}$, a parte real de $\begin{array}{r}S\end{array}$) e potência reativa ($\begin{array}{r}Q\end{array}$, a parte imaginária de $\begin{array}{r}S\end{array}$). A potência ativa $\begin{array}{r}P\end{array}$ corresponde à potência consumida pelos elementos resistivos do circuito, transformada em calor pelo efeito Joule. Sua unidade é Watts (W). A potência reativa $\begin{array}{r}Q\end{array}$ corresponde à potência circulante no circuito devido aos elementos armazenadores de energia (capacitor e indutor). Ora essa energia é fornecida pelas fontes do circuito, ora ela é devolvida pelos capacitores/indutores. Sua unidade é VA reativos (VAr). Pelo triângulo das potências, podemos relacionar $\begin{array}{r}P\end{array}$, $\begin{array}{r}Q\end{array}$ e $\begin{array}{r}S\end{array}$ da seguinte maneira: $\begin{array}{r}P=|S|\cos (\varphi )\end{array}$ $\begin{array}{r}Q=|S|\sin (\varphi )\end{array}$ $\begin{array}{r}|S|=\sqrt{P^2+Q^2}\end{array}$ $\begin{array}{r}\varphi ={\cos }^{-1}\left(\frac{P}{Q}\right)\end{array}$ em que $\begin{array}{r}\varphi ={\theta }_V-{\theta }_i\end{array}$ é a defasagem entre tensão e corrente no elemento considerado.

5 Listas de Exercícios

Lista 01: Análise Transitória RC/RL

Figura 1a: Células fotovoltaícas na estação espacial*. Figura 1b: Circuito com fotocélulas*. Figura 2: Circuito com elementos armazenadores de energia. Em t=0, a fonte de -1 V é desligada e a fonte de 1 V é ligada. Figura 3a: Uma fonte de energia de 240 W*. Figura 3b: Modelo da fonte de energia da Figura 3a*. (1 - DORF/SVOBODA*) As células fotovoltaicas da estação espacial proposta na Figura 1a fornecem a tensão elétrica $v(t)$ do circuito mostrado na Figura 1b. A estação espacial passa atrás da sombra da terra (em $t=0$) com tensão $v(0)=2\text{ Volts}$ e $i(0)=0.1\text{ A}$. Faça um esboço da tensão $v(t)$ para $t\ge 0$ até o seu regime permanente $(t\approx 5s)$. Use o simulador de circuitos para auxiliar. (2 - DORF/SVOBODA*) Determine $i(t)$ e $v(t)$ (em regime permanente) para $t<0$ e para $t>0$ para o circuito da Figura 2. (3 - DORF/SVOBODA*) Uma fonte de alimentação de 240 W é mostrada na Figura 3a. Este circuito emprega um indutor e um capacitor de grande porte. O modelo do circuito é apresentado na Figura 3b. Encontre $i_L(t)$ (em regime permanente) para $t<0$ (antes da abertura da chave) e para $t>0$ (após a abertura da chave) no circuito da Figura 3b. Para $t<0$, assuma condições de regime permanente antes da abertura da chave. Simule o circuito e faça um esboço da corrente no indutor. (4) Repita o exercício anterior para a corrente $i_{8\mathrm{\Omega }}(t)$ (no resistor de $8\mathrm{\Omega }$) e calcule a potência dissipada no resistor para os dois casos. *DORF, Richard C.; SVOBODA, James A. Introdução Aos Circuitos Elétricos. LTC - GRUPO GEN, 8a Ed. 2012, ISBN 9788521621164.

Lista 02: Análise em Regime Permanente Senoidal

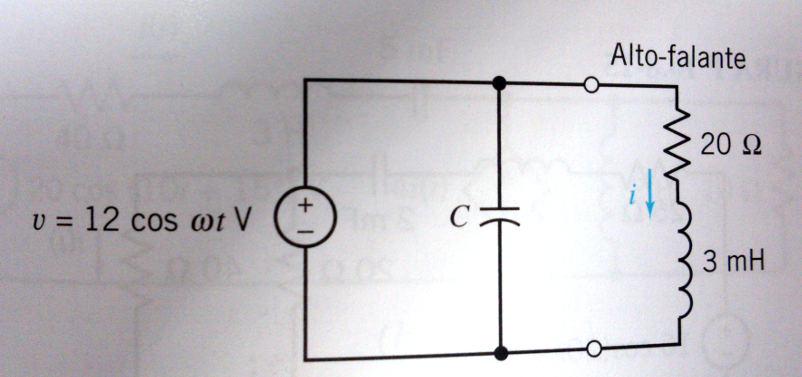
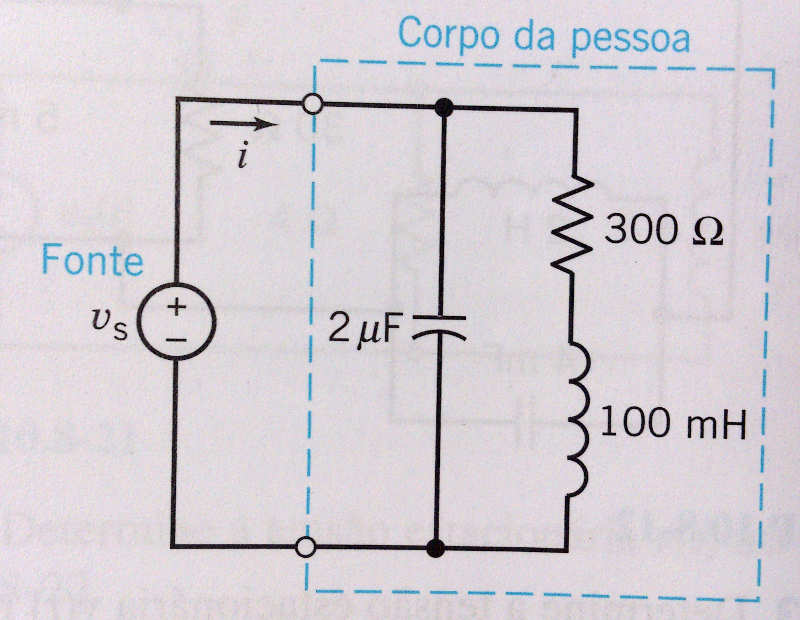
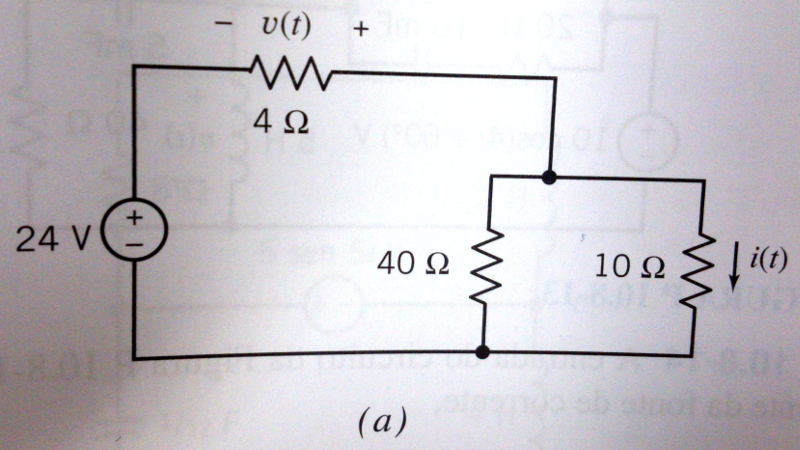
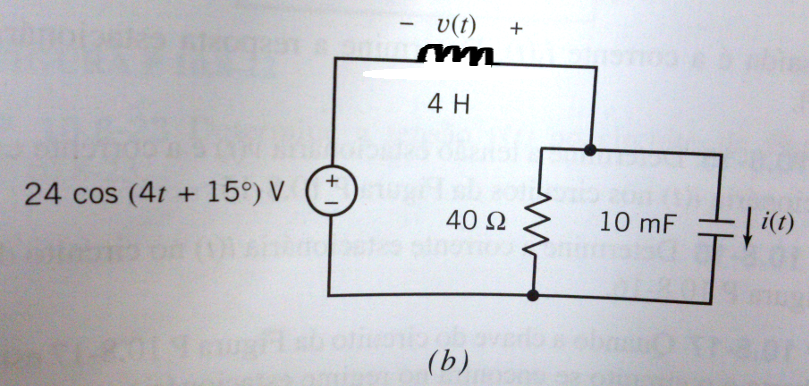
Figura P10.8-5: Circuito de um sintetizador*. Figura P10.8-9: Circuito equivalente do corpo durante o choque*. Figura P10.8-10a: Circuito resistivo DC*. Figura P10.8-10b: Circuito RLC em regime permanente senoidal*. (P10.8-5 - DORF/SVOBODA*) Uma das atrações do filme Quero Ser Grande é um piano gigantesco tocado com os pés. O criador do piano usou um sintetizador acoplado a um alto-falante, como mostra a Figura 10.8-5 (Gardner, 1998). Determine a corrente $i(t)$ para uma nota musical de $796$ $\mathrm{H}\mathrm{z}$ se $C=10$ $\mathrm{\mu }\mathrm{F}$. (P10.8-9 - DORF/SVOBODA*) Todo ano, 500 a 1000 pessoas morrem nos Estados Unidos por causa de choques elétricos. Se uma pessoa faz um bom contato elétrico com as mãos, o circuito pode ser representado pela Figura P10.8-9, onde $v_s(t)=160\cos (\omega t)$ $\mathrm{V}$ e $\omega =2\pi f$. Determine a corrente estacionária que atravessa o corpo: (a) para $f=60$ $\mathrm{H}\mathrm{z}$; (b) para $f=400$ $\mathrm{H}\mathrm{z}$. (P10.8-10 - DORF/SVOBODA*, adaptado.) Nos circuitos das Figuras P10.8-10a e P10.8-10b, determine a função de transferência $G(\omega )$ considerando a tensão $v(t)$ com sendo a tensão de saída $V_{out}$. *DORF, Richard C.; SVOBODA, James A. Introdução Aos Circuitos Elétricos. LTC - GRUPO GEN, 8a Ed. 2012, ISBN 9788521621164.

5.1 Exercícios Complementares

Lista 01b: Sinal Senoidal

Lista 02b: Sinal Senoidal (Gráficos)

Lista 03b: Reatâncias e Impedância

Lista 04b: Reatâncias e Impedância

Lista 05a: Resolver usando Teorema da Superposição e Análise de Malhas

Lista 05b: Resolver usando Teorema da Superposição e Análise Nodal

6 Professores

• 2015-2 - Bruno Fontana da Silva
  

Voltar

Curso Técnico Integrado de Telecomunicações