Transformadas de Fourier

1 Transformada de Fourier no tempo contínuo (TFTC)

O sinal $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ é contínuo no tempo, e o sinal $\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}$ é contínuo na frequência.

A equação de análise

É uma transformação de um domínio de uma variável real $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ de tempo continuo em uma variável complexa $\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}$ de frequência contínua.

$\mathrm{D}\mathrm{T}\mathrm{\to }\mathrm{D}\mathrm{F}$.

$\mathrm{x}\mathrm{:}\mathbb{ℝ}\mathrm{\to }\mathbb{ℂ}$.

$$\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}\mathrm{\equiv }{ℱ}\mathrm{\{}\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\underset{\mathrm{-}\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\Omega }\mathrm{t}}\mathrm{d}\mathrm{t}$$

A equação de síntese

É uma transformação de um domínio de uma variável complexa $\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}$ de frequência contínua em uma variável real $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ de tempo continuo.

$\mathrm{D}\mathrm{F}\mathrm{\to }\mathrm{D}\mathrm{T}$.

$\mathrm{X}\mathrm{:}\mathbb{ℂ}\mathrm{\to }\mathbb{ℝ}$.

$$\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}\mathrm{\equiv }{{ℱ}}^{\mathrm{-}\mathrm{1}}\mathrm{\{}\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{2\pi }\underset{\mathrm{-}\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}{\mathrm{e}}^{\mathrm{j}\mathrm{\Omega }\mathrm{t}}\mathrm{d}\mathrm{\Omega }$$

A transformada de Fourier $\mathrm{X}\mathrm{(}\mathrm{j}\mathrm{\Omega }\mathrm{)}$, por simplificação é muitas vezes representada apenas por $\mathrm{X}\mathrm{(}\mathrm{\Omega }\mathrm{)}$ ou $\mathrm{X}\mathrm{(}\mathrm{\omega }\mathrm{)}$, mas é importante lembrar que tratasse de uma frequência complexa, representada pelo eixo imaginário do plano s.

Figura 1 - Sinal $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ e sua transformada de Fourier $\mathrm{X}\mathrm{(}\mathrm{\Omega }\mathrm{)}$ Fonte: Elaborado pelo autor.

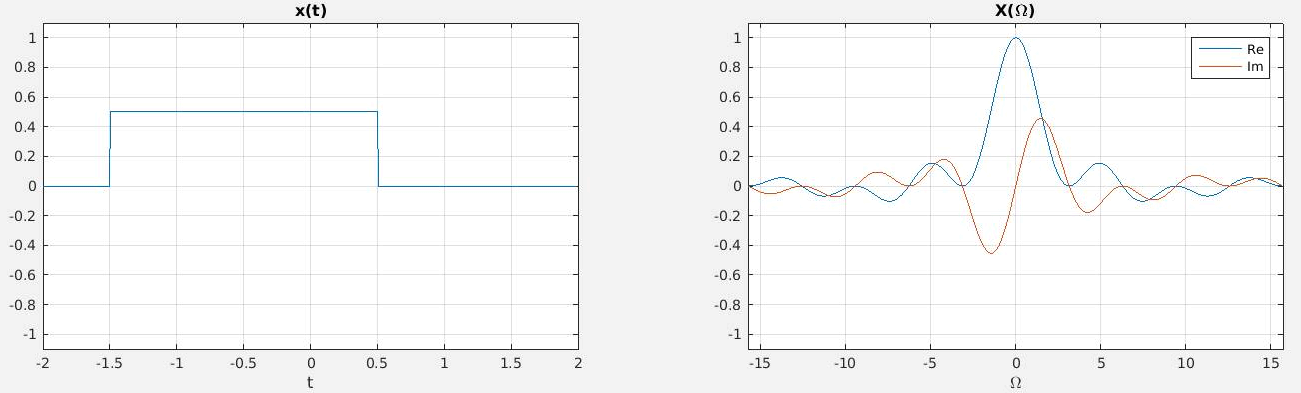
• Para relembrar os conceitos vistos em Sinais e Sistemas, recomendo assitir os vídeos sobre Transformada de Fourier do prof. Luis Antonio Aguirre da UFMG

Introdução a Transformada de Fourier	Existência da Transformada Fourier	Transformada de Fourier: Propriedades 1	Transformada de Fourier: Propriedades 2	Transformada de Fourier para Sinais Periodicos
Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar

2 Transformada Z

A transformada Z de um sinal de tempo discreto $x(n)$ é a função $X(z)$ definida como

$X(z)=Z\{x(n)\}=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(n)z^{-n}$

onde $n$ é um inteiro; $z=A{e}^{j\varphi }$ é um número complexo, com $A$ sendo sua magnitude, e $\varphi$ sua frequência angular (em radianos por amostra).

A transformada Z inversa é

$x(n)=Z^{-1}\{X(z)\}=\frac{1}{2\pi j}{\oint }_{C}X(z)z^{n-1}dz$

onde $C$ é o caminho antihorário envolvendo a origem, dentro da região de convergencia (ROC) de $X(z)$.

3 Transformada de Fourier de tempo discreto (TFTD)

O sinal $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ é discreto no tempo, e o sinal $\mathrm{X}\mathrm{(}\mathrm{\Omega }\mathrm{)}$ é contínuo e periódico em $\mathrm{2}\mathrm{\pi }$.

A equação de análise

É uma transformação de um domínio de uma variável real $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ de tempo discreto em uma variável complexa $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}$ frequência contínua periódica.

$\mathrm{D}\mathrm{T}\mathrm{\to }\mathrm{D}\mathrm{F}$.

$\mathrm{x}\mathrm{:}\mathbb{ℝ}\mathrm{\to }\mathbb{ℂ}$.

$$\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{\equiv }{ℱ}\mathrm{\{}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\omega }\mathrm{n}}$$

A equação de síntese

É uma transformação de um domínio de uma variável complexa $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}$ de frequência contínua periódica em uma variável real $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ continua.

$\mathrm{D}\mathrm{F}\mathrm{\to }\mathrm{D}\mathrm{T}$.

$\mathrm{X}\mathrm{:}\mathbb{ℂ}\mathrm{\to }\mathbb{ℝ}$.

$$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{\equiv }{{ℱ}}^{\mathrm{-}\mathrm{1}}\mathrm{\{}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{2\pi }\underset{\mathrm{-}\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }\mathrm{n}}\mathrm{d}\mathrm{\omega }$$

Como a transformada de Fourier $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}$ é periódica com período $\mathrm{2}\mathrm{\pi }$, pois $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{=}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{\omega }\mathrm{+}\mathrm{2}\mathrm{\pi }\mathrm{k}\mathrm{)}}\mathrm{)}$, para $\mathrm{k}\mathrm{\in }\mathbb{\mathbb{Z}}$, ela pode ser calculada em qualquer faixa de $\mathrm{2}\mathrm{\pi }$, por exemplo $\mathrm{\omega }\mathrm{\in }\mathrm{[}\mathrm{-}\mathrm{\pi },\mathrm{\pi }\mathrm{)}$.

$$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{\equiv }{{ℱ}}^{\mathrm{-}\mathrm{1}}\mathrm{\{}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{2\pi }\underset{\mathrm{-}\mathrm{\pi }}{\overset{\mathrm{\pi }}{\int }}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }\mathrm{n}}\mathrm{d}\mathrm{\omega }$$

Figura 2 - Sinal discreto $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ e sua TFDT $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}$ Fonte: Elaborado pelo autor.

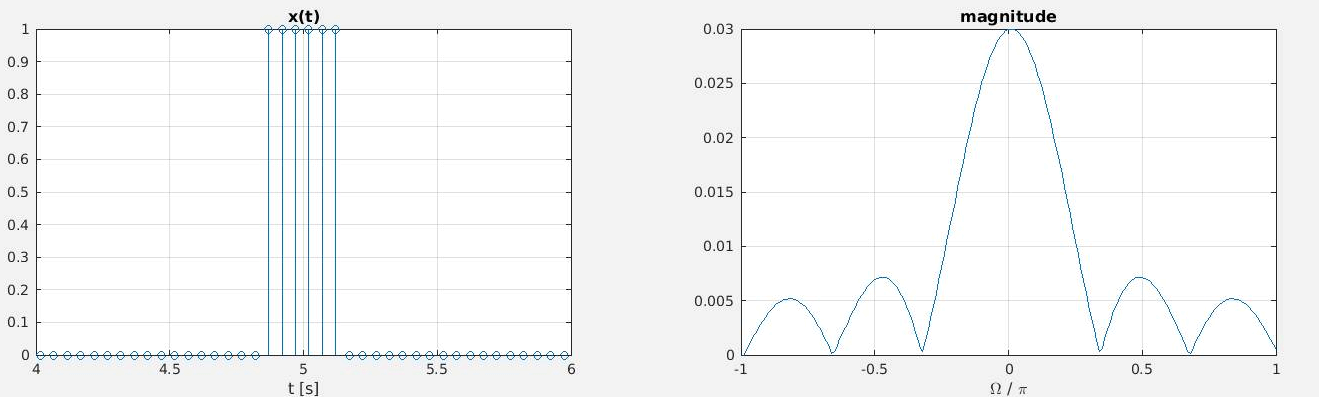
4 Série de Fourier de tempo contínuo (SF)

O sinal $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ é contínuo e periódico no tempo (com período $T$) , e o sinal $\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}$ é discreto na frequência.

A equação de análise

É uma transformação de um domínio de uma variável real $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ de tempo continuo em uma variável complexa $\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}$ de frequência discreta.

$\mathrm{D}\mathrm{T}\mathrm{\to }\mathrm{D}\mathrm{F}$.

$\mathrm{x}\mathrm{:}\mathbb{ℝ}\mathrm{\to }\mathbb{ℂ}$.

$X(k)=\frac{1}{T}\underset{0}{\overset{T}{\int }}x(t)e^{-j(2\pi /T)kt)}\mathrm{d}t$

A equação de síntese

É uma transformação de um domínio de uma variável complexa $\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}$ de frequência contínua em uma variável real $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ de tempo continuo.

$\mathrm{D}\mathrm{F}\mathrm{\to }\mathrm{D}\mathrm{T}$.

$\mathrm{X}\mathrm{:}\mathbb{ℂ}\mathrm{\to }\mathbb{ℝ}$.

$x(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}X(k)e^{j(2\pi /T)kt)}$

A série de Fourier $\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}$, indicada acima é a série exponencial onde as funções de base são exponenciais complexas $e^{-j\omega t}$, onde $\omega =(2\pi /T)k$. Também existem as séries de Fourier usando funções de base senoidais e cossenoidais, as quais podem ser derivadas da série exponencial.

Figura 3 - Sinal $\mathrm{x}\mathrm{(}\mathrm{t}\mathrm{)}$ periódico e sua série de Fourier $\mathrm{X}\mathrm{(}\mathrm{\Omega }\mathrm{)}$ Arquivo:SerieFourierPlot.png Fonte: Elaborado pelo autor.

5 Transformada de Discreta de Fourier (TDF)

5.1 Obtenção da TDF a partir da amostragem da TFTD

Sinais discretos no tempo podem ser representados pela sua TFTD, que é uma função continua periódica em $\mathrm{2}\mathrm{\pi }$ de $\mathrm{\omega }$ :

$\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\omega }\mathrm{n}}$

Para que a mesma possa ser utilizada no processamento de sinais digitais é necessário que a variável frequência seja também discreta. Se amostrarmos uniformemente a frequência $\mathrm{\omega }$ em N amostras entre 0 e $\mathrm{2}\mathrm{\pi }$ é possível obter a TDF (ou DFT - Discrete Fourier Transform). Assim se tomarmos N frequências ${\mathrm{\omega }}_{\mathrm{k}}\mathrm{=}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}$ com $k\in \mathbb{\mathbb{Z}}$, and $\mathrm{0}\mathrm{\le }\mathrm{k}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$, obtemos o espectro amostrado uniformemente:

${\mathrm{X}}^{\prime }\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{=}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\sum _{\mathrm{k}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{\delta }(\omega -\frac{2\pi }{N}k)$.

${\mathrm{X}}^{\prime }\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\frac{2\pi }{N}\mathrm{k}\mathrm{n}}$

O sinal equivalente no tempo pode ser obtido aplicando a transformada inversa e a convolução:

${\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{=}{{ℱ}}^{\mathrm{-}\mathrm{1}}\mathrm{\{}{\mathrm{X}}^{\prime }\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{\}}\mathrm{=}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{*}(\frac{N}{2\pi }\sum _{p=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (n-Np))\mathrm{=}\frac{N}{2\pi }\sum _{\mathrm{p}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{-}\mathrm{N}\mathrm{p}\mathrm{)}$.

O que mostra que o sinal Esse sinal ${\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}$ são repetições periódicas (com período N) do sinal discreto $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ original.

• Note que N o período de repetição do sinal ${\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}$ é o mesmo período de repetição das N amostras da TFTD $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}$ original.
• Se o comprimento L o sinal do $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ for maior que N o período de repetição do sinal ${\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}$, haverá sobreposição das amostras no tempo (time aliasing), e não será possível recuperar o sinal original.
• Por outro lado, se $\mathrm{L}\mathrm{\le }\mathrm{N}$ então ${\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}$ é a repetição periódica exata de $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$.

$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{=}\frac{2\pi }{N}{\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}$ , para $\mathrm{0}\mathrm{\le }\mathrm{n}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$ ou

$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{=}\frac{2\pi }{N}{\mathrm{x}}^{\prime }\mathrm{(}\mathrm{n}\mathrm{)}[u(n)-u(n-N)$.

Portanto, é possível recuperar as amostras do sinal digital no tempo $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ a partir das suas amostras digitais na frequência, desde que o período de repetição das N amostras de frequência seja maior ou igual ao comprimento L do sinal no tempo.

5.2 DFT e IDFT

• O sinal $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ é discreto no tempo pode ser representado pelo o sinal $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}$ discreto e periódico em $\mathrm{2}\mathrm{\pi }$.

Para obter a equação de análise (DFT) pode ser feito o cálculo das amostras do espectro de frequências em ${\mathrm{\omega }}_{\mathrm{k}}\mathrm{=}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}$ em:

$\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\omega }\mathrm{n}}$

$\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}\mathrm{n}}$

Conforme mostrado, o espectro é periódico em N, e portanto é suficiente calcular apenas os valores para $\mathrm{0}\mathrm{\le }\mathrm{k}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$. Assim obtém-se

A equação de análise (DFT)

É uma transformação de um domínio de uma variável real $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ de tempo discreto em uma variável complexa $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}$ frequência discreta periódica.

$\mathrm{D}\mathrm{T}\mathrm{\to }\mathrm{D}\mathrm{F}$.

$\mathrm{x}\mathrm{:}\mathbb{ℝ}\mathrm{\to }\mathbb{ℂ}$.

$\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}\mathrm{\equiv }{ℱ}\mathrm{\{}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{0}}^{\mathrm{N}\mathrm{-}\mathrm{1}}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}\mathrm{n}}$ , para $\mathrm{0}\mathrm{\le }\mathrm{k}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$

A equação de síntese (IDFT)

É uma transformação de um domínio de uma variável complexa $\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}$ de frequência discreta periódica em uma variável real $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ discreta.

$\mathrm{D}\mathrm{F}\mathrm{\to }\mathrm{D}\mathrm{T}$.

$\mathrm{X}\mathrm{:}\mathbb{ℂ}\mathrm{\to }\mathbb{ℝ}$.

$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{\equiv }{{ℱ}}^{\mathrm{-}\mathrm{1}}\mathrm{\{}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}\mathrm{\}}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{N}\sum _{\mathrm{k}\mathrm{=}\mathrm{0}}^{\mathrm{N}\mathrm{-}\mathrm{1}}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}\mathrm{n}}$ , para $\mathrm{0}\mathrm{\le }\mathrm{n}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$

Ao usar a equação de análise, se o comprimento L de $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ for menor que o período de repetição N, é necessário que $\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}$ seja preenchido com amostras nulas até atingir o comprimento N (zero-padding).

Simplificação da notação

Para simplificar a notação é podemos utilizar:

$\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}\mathrm{=}\mathrm{X}\mathrm{(}{\mathrm{e}}^{\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{)}$ para a frequência discreta periódica.

E ainda definir:

${\mathrm{W}}_{\mathrm{N}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{2}\mathrm{\pi }/\mathrm{N}}$ como a frequência fundamental

Essa frequência pode ser representada como uma posição no circulo unitário do plano complexo :$z$.

Alguns valores de Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \mathrm{W_N \ } que ajudam a lembrar as simplificações:

${\mathrm{W}}_{\mathrm{1}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{2}\mathrm{\pi }}=+1$

${\mathrm{W}}_{\mathrm{-}\mathrm{1}}\mathrm{=}{\mathrm{e}}^{\mathrm{j}\mathrm{2}\mathrm{\pi }}=+1$

${\mathrm{W}}_{\mathrm{2}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\pi }}=-1$

${\mathrm{W}}_{\mathrm{-}\mathrm{2}}\mathrm{=}{\mathrm{e}}^{\mathrm{j}\mathrm{\pi }}=-1$

${\mathrm{W}}_{\mathrm{4}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{\pi }/\mathrm{2}}=-j$

${\mathrm{W}}_{\mathrm{-}\mathrm{4}}\mathrm{=}{\mathrm{e}}^{\mathrm{j}\mathrm{\pi }/\mathrm{2}}=+j$

Também é importante lembrar que se $N$ é múltiplo de $k$ então:

$W_{\mathrm{N}}^{\mathrm{k}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{(}\mathrm{2}\mathrm{\pi }/\mathrm{N}\mathrm{)}\mathrm{k}}\mathrm{=}{\mathrm{e}}^{\mathrm{-}\mathrm{j}\mathrm{2}\mathrm{\pi }/\mathrm{(}\mathrm{N}/\mathrm{k}\mathrm{)}}\mathrm{=}{\mathrm{W}}_{\mathrm{N}/\mathrm{k}}$

Dessa forma as equações da DFT e IDFT passam a ser escritas de forma simplificada como:

$\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}\mathrm{=}\sum _{\mathrm{n}\mathrm{=}\mathrm{0}}^{\mathrm{N}\mathrm{-}\mathrm{1}}\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}{W}_{\mathrm{N}}^{\mathrm{k}\mathrm{n}}$ , para $\mathrm{0}\mathrm{\le }\mathrm{k}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$

$\mathrm{x}\mathrm{(}\mathrm{n}\mathrm{)}\mathrm{=}\frac{1}{N}\sum _{\mathrm{k}\mathrm{=}\mathrm{0}}^{\mathrm{N}\mathrm{-}\mathrm{1}}\mathrm{X}\mathrm{(}\mathrm{k}\mathrm{)}{W}_{\mathrm{N}}^{\mathrm{-}\mathrm{k}\mathrm{n}}$ , para $\mathrm{0}\mathrm{\le }\mathrm{n}\mathrm{\le }\mathrm{N}\mathrm{-}\mathrm{1}$

Dessas equações é possível perceber que o cálculo da DFT e da IDFT requerem a ${\mathrm{N}}^{\mathrm{2}}$ multiplicações e $\mathrm{N}\mathrm{(}\mathrm{N}\mathrm{-}\mathrm{1}\mathrm{)}$ somas, sendo portanto um algoritmo de $\mathrm{O}\mathrm{(}{\mathrm{N}}^{\mathrm{2}}\mathrm{)}$.

5.3 Transformada Rápida de Fourier (FFT)

As FFTs são algoritmos que reduzem a complexidade do cálculo da DFT, obtendo ordens de $\mathrm{O}\mathrm{(}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N}\mathrm{\times }\mathrm{N}\mathrm{)}$.

• Para relembrar os conceitos vistos acima, recomendo assistir os vídeos sobre DFT do prof. Steve Brunton da University of Washington

The Discrete Fourier Transform (DFT)	Computing the DFT Matrix	The Fast Fourier Transform (FFT)	The Fast Fourier Transform Algorithm
Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade Continuar Dispensar

6 Soma dos termos de uma Progressão Geométrica

A soma aritmética dos termos de uma P.G. a partir do primeiro termo, é definida por:

$S_n==a_1+a_{1}q+a_1{q}^2+\dots +a_1{q}^{n-1}=\sum _{i=1}^n{a}_1{q}^{i-1}$

Caso $q\ne 1$, a soma pode ser descrita por:

$S_n=\frac{a_1(1-q^n)}{1-q}$