FIC MATLAB 2018-2: mudanças entre as edições
| Linha 18: | Linha 18: | ||
=== Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição === | == Conteúdos Abordados == | ||
{{collapse top| bg=lightblue | 11/Set}} | |||
=== 1 - Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição === | |||
{{collapse top| bg=lightblue | 11/Set - }} | |||
* MATLAB e Octave; | * MATLAB e Octave; | ||
| Linha 107: | Linha 109: | ||
:::<math>d = \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)}</math> | :::<math>d = \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)}</math> | ||
:::<math> | :::<math>d = 5{,}2 \cos^2 \left( \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)} \right)</math> | ||
* Ajudas: | * Ajudas: | ||
| Linha 160: | Linha 163: | ||
* [[FIC_MATLAB_2018-2/Aula-1|Códigos executados na aula]] | * [[FIC_MATLAB_2018-2/Aula-1|Códigos executados na aula]] | ||
{{collapse bottom}} | |||
=== 2 - Vetores e matrizes === | |||
{{collapse top| bg=lightblue | 13/Set}} | |||
* Definições de vetores; | |||
* Definições de matrizes; | |||
* Comandos ''length'' e ''size''; | |||
* Arranjo de vetores: | |||
:* Utilizando dois pontos (:); | |||
::* Definição de passo; | |||
:* Comandos ''linspace'' e ''logspace''; | |||
* '''Exercícios:''' | |||
:1. Crie os vetores descritos abaixo usando dois métodos diferentes: | |||
::a) Início: 5, Fim: 28, com 100 elementos regularmente espaçados. | |||
::b) Início: 5, Fim: 14, com passo de 0,2. | |||
::c) Início: -2, Fim: 5, com 50 elementos regularmente espaçados. | |||
::d) Início: 100, Fim: 12, com 100 elementos regularmente espaçados. | |||
:2. Crie os vetores descritos abaixo: | |||
::a) Início: 10, Fim: 1000, com 50 elementos logaritmicamente espaçados. | |||
::b) Início: 0,01, Fim: 1, com 20 elementos logaritmicamente espaçados. | |||
:3. Crie um vetor '''x''' que tenha 6 valores entre 0 e 10. Em seguida, crie uma matriz '''A''' cuja primeira linha contenha os valores 3'''x''' e segunda linha contenha os valores 5'''x''' - 20. | |||
:4. Repita o exercício anterior, substituindo a palavra ''linha'' por ''coluna''. | |||
:5. Crie o vetor ''v = [2 4 8 16 32 ... 512 1024]'' utilizando o comando ''logspace''. | |||
* Definições de matrizes ''eye'', ''zeros'' e ''ones''; | |||
:* Usando ''length'' e ''size'' na criação de matrizes; | |||
* Matriz transposta ( .' ) e matriz Hermitiana ('); | |||
* [[FIC_MATLAB_2018-2/Aula-2|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 3 - Operações com matrizes; Plots === | |||
{{collapse top| bg=lightblue | 18/Set}} | |||
* Operações; | |||
:* Soma e diferença; | |||
:* Produto matricial; | |||
:* Produto e divisão elemento a elemento; | |||
:* Potenciação; | |||
:* Funções (''sin'', ''log'', etc) aplicadas a matrizes; | |||
:* Operações entre matrizes e escalares; | |||
:* Comandos ''sum'' e ''prod''; | |||
:* Mínimo (''min''), máximo (''max''), média (''mean'') e norma (''norm''); | |||
:* Determinante (''det'') e inversa (''inv'') de uma matriz; | |||
* '''Exercícios:''' | |||
:1. Defina as matrizes abaixo: | |||
:::<math> | |||
A = \begin{bmatrix} | |||
1 & 2 & 3 & 4 & 5\\ | |||
6 & 7 & 8 & 9 & 10\\ | |||
11 & 12 & 13 & 14 & 15\\ | |||
16 & 17 & 18 & 19 & 20 | |||
\end{bmatrix} | |||
\qquad | |||
B = \begin{bmatrix} | |||
1/2 & 1/3\\ | |||
1/4 & 1/5\\ | |||
1/6 & 1/7\\ | |||
1/8 & 1/9 | |||
\end{bmatrix} | |||
\qquad | |||
C = \begin{bmatrix} | |||
-1/12 & 1/{-3}\\ | |||
0 & 0\\ | |||
1 & 17\\ | |||
2 & 19 | |||
\end{bmatrix} | |||
\qquad | |||
D = \begin{bmatrix} | |||
\sqrt 2\\ | |||
\pi\\ | |||
e\\ | |||
\sqrt 3\\ | |||
42 | |||
\end{bmatrix} | |||
</math> | |||
:2. Para as matrizes acima, realize as operações abaixo: | |||
::a) B + C | |||
::b) A D (multiplicação matricial) | |||
::c) C B<sup>T</sup> A | |||
::d) X = B<sup>T</sup> C | |||
::e) X<sup>2</sup> | |||
::f) B C (multiplicação elemento a elemento) | |||
:3. Crie o vetor ''v = [1 4 9 16 25 ... 81 100]''. | |||
:4. Crie o vetor ''v = [2 4 8 16 32 ... 512 1024]'' sem utilizar o comando ''logspace''. | |||
:5. Utilize o MATLAB para calcular 12! (isto é, o fatorial do número 12), sem utilizar o comando ''factorial''. | |||
:6. O [https://pt.wikipedia.org/wiki/S%C3%A9rie_harm%C3%B3nica_(matem%C3%A1tica) número harmônico] <math>H_n</math> é definido como sendo a soma ''1 + 1/2 + ... + 1/n''. Utilize o MATLAB para calcular <math>H_{100}</math>. | |||
:7. Seja | |||
:::::<math> | |||
x = 1 + 1/4 + 1/9 + 1/16 + 1/25 + \cdots + 1/10000^2. | |||
</math> | |||
::Calcule ''x''. Em seguida, calcule <math>\sqrt{6x}</math>. | |||
* Plots: | |||
:* Comandos ''plot'', ''stem'', ''bar'' e ''stairs'' de uma função | |||
::* Uso de apenas um parâmetro | |||
:* Comando ''hold'' para manter a curva no gráfico | |||
:* Comando ''grid'' para mostrar linhas em forma de grade | |||
:* Nomes aos eixos com ''xlabel'' e ''ylabel'' | |||
:* Comando ''title'' | |||
:* Comandos ''axis'', ''xlim'' e ''ylim'' para ajuste de eixos | |||
:* Comando ''legend'' | |||
:* Especificadores de linha, cores e marcadores: | |||
:::{| class="wikitable" | |||
! '''Tipo de linha''' | |||
! '''Símbolo''' | |||
|- | |||
| Sólida (padrão) || - | |||
|- | |||
| Tracejada || -- | |||
|- | |||
| Tracejada com pontos || -. | |||
|- | |||
| Com pontos || : | |||
|} | |||
:::{| class="wikitable" | |||
! '''Cores''' | |||
! '''Símbolo''' | |||
|- | |||
| Preto || k | |||
|- | |||
| Azul || b | |||
|- | |||
| Ciano || c | |||
|- | |||
| Verde || g | |||
|- | |||
| Magenta || m | |||
|- | |||
| Vermelho || r | |||
|- | |||
| Branco || w | |||
|- | |||
| Amarelo || y | |||
|} | |||
:::{| class="wikitable" | |||
! '''Marcadores de dados''' | |||
! '''Símbolo''' | |||
|- | |||
| Ponto || . | |||
|- | |||
| Asterisco || * | |||
|- | |||
| Cruz || x | |||
|- | |||
| Círculo || o | |||
|- | |||
| Adição || + | |||
|- | |||
| Quadrado || s | |||
|- | |||
| Losango || d | |||
|- | |||
| Triângulo apontando pra cima || ^ | |||
|- | |||
| Triângulo apontando pra baixo || v | |||
|- | |||
| Triângulo apontando pra direita || > | |||
|- | |||
| Triângulo apontando pra esquerda || < | |||
|- | |||
| Estrela de 5 pontas || p | |||
|- | |||
| Estrela de 6 pontas || h | |||
|} | |||
* [[FIC_MATLAB_2018-2/Aula-3|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 4 - Exercícios plot; Números aleatórios === | |||
{{collapse top| bg=lightblue | 20/Set}} | |||
* '''Exercícios''' (Plots) | |||
:1. Plote, em um mesmo gráfico, as funções | |||
:::::<math>f(x) = \sqrt{1 - |x - 1|^2}</math> | |||
::e | |||
:::::<math>\displaystyle{g(x) = \arccos(1 - |x|) - \pi},</math> | |||
::para <math>-2 \leq x \leq 2</math>. | |||
:2. Plote a função <math>\displaystyle{f(x) = x^2 + x - 2}</math> de -4 até 4 e encontrar as raízes por Bhaskara. | |||
:3. Utilize o MATLAB para plotar a função <math>\displaystyle{T = 3 \ln (2 t) - 5 e^{0,5 t}}</math> ao longo do intervalo <math>1 \leq t \leq 3</math>. Insira um título na plotagem e rotule adequadamente os eixos. A variável ''T'' representa a temperatura em graus Celsius; a variável ''t'' representa o tempo em minutos. | |||
:4. Plote as funções <math>\displaystyle{u = 100 \log_{10} (60 x + 1)}</math> e <math>\displaystyle{v = 50 \cos(6 x) \mathrm{sen} (2 x) + 150 x}</math> ao longo do intervalo <math>0 \leq x \leq 2</math>. Rotule adequadamente a plotagem e cada uma das curvas, utilizando '''legend'''. A variável ''u'' representa a velocidade de uma Ferrari em km/h. A variável ''v'' representa a velocidade de um Fusca. | |||
:5. Use a função ''stem'' para plotar os sinais abaixo na mesma figura: | |||
:: <math>\displaystyle{\cos(x)}</math>, para <math>0 \leq x \leq 2 \pi</math> | |||
:: <math>\displaystyle{0,5 \sin(x)}</math>, para <math>\pi \leq x \leq 3 \pi</math> | |||
:6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função | |||
:::::<math>f(x) = | |||
\begin{cases} | |||
-1, & -\pi \leq x \leq 0 \\ | |||
1, & 0 \leq x \leq \pi | |||
\end{cases}</math> | |||
::é | |||
:::::<math>g(x) = \frac{4}{\pi} \left( \frac{\sin(x)}{1} + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5} + \frac{\sin(7x)}{7} + \cdots \right)</math>. | |||
::Plote, em um mesmo gráfico, a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando os quatro termos explicitados. Considere ''x'' na faixa de <math>-\pi</math> até <math>\pi</math>. | |||
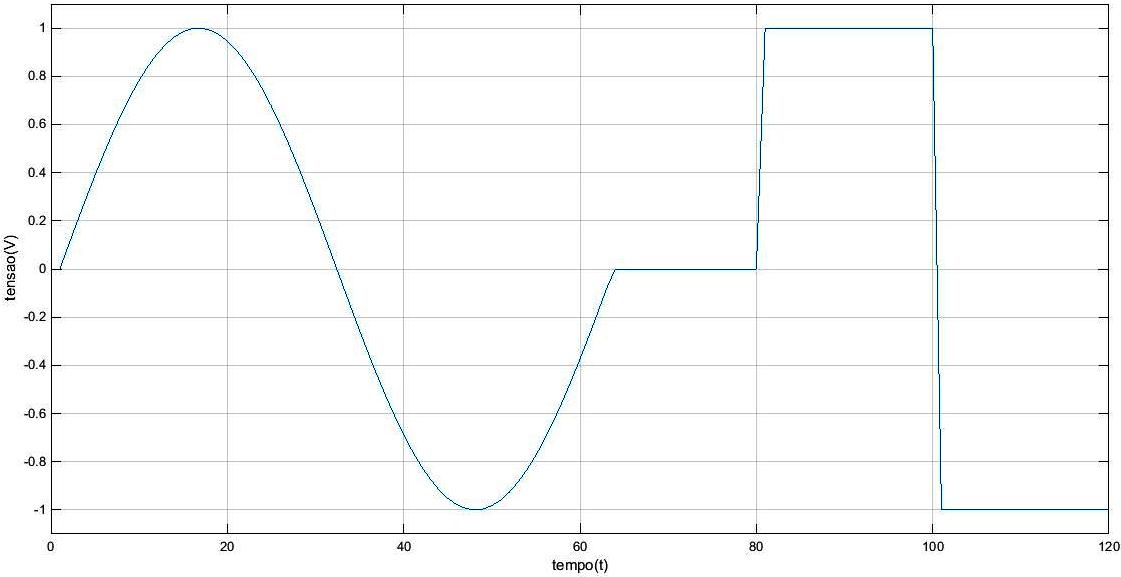
:7. Fazer o ''plot'' de um sinal de tensão versus tempo, como da figura: | |||
:::::<math>f(t) = | |||
\begin{cases} | |||
\sin(2 \pi t / 63), & \text{de } t = 1s \text{ ate } t = 63s \\ | |||
0, & \text{de } t = 64s \text{ ate } t = 80s \\ | |||
1, & \text{de } t = 81s \text{ ate } t = 100s \\ | |||
-1, & \text{de } t = 101s \text{ ate } t = 120s | |||
\end{cases}</math> | |||
:: Não esquecer de nomear os eixos. | |||
[[Image:Exercícios Aula 3 FIC Matlab.jpg|600px|center]] | |||
* Outros comandos relacionados a plotagem: | |||
:* Comando ''figure'' | |||
:* Comando ''subplot'' | |||
:* Comando ''close all'' para fechar todas figuras | |||
* Números aleatórios | |||
:* Comando ''randi'' para valores inteiros uniformemente distribuídos | |||
:* Comando ''rand'' para valores uniformemente distribuídos | |||
:* Comando ''randn'' para valores normalmente distribuídos | |||
:* Comando ''hist'' e ''histogram'' para cálculo/visualização do histograma | |||
* [[FIC_MATLAB_2018-2/Aula-4|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 5 - Endereçamento e concatenação de vetores e matrizes; Repmat e Reshape === | |||
{{collapse top| bg=lightblue | 25/Set}} | |||
* Endereçamento de vetores e matrizes | |||
:* Indexação de um elemento | |||
::* Índice | |||
::* Subscrito | |||
:* Submatrizes | |||
::* Índice | |||
::* Subscrito | |||
:* Palavra-chave ''end'' | |||
:* Indexação/submatrizes do lado esquerdo vs do lado direito | |||
:* Exclusão de linha ou coluna | |||
* [[FIC_MATLAB_2018-2/Aula-5|Códigos executados na aula]] | |||
* '''Exercícios:''' | |||
:1. Crie uma matriz '''A''' de tamanho 15 x 15 de inteiros. | |||
::a) Extraia o elemento da segunda linha e quarta coluna de '''A''', armazenando na variável ''u'' | |||
::b) Crie um vetor '''v''' formado pelos elementos da segunda coluna de '''A''' | |||
::c) Crie um vetor '''w''' formado pelos elementos da última linha de '''A''' | |||
::d) Crie uma matriz '''B''' formada pelos elementos da segunda até a décima coluna de '''A''' | |||
::e) Crie uma matriz '''C''' formada pelos elementos da quinta até a penúltima linha de '''A''' | |||
::f) Crie uma matriz '''D''' formada pelos elementos da sétima até a penúltima linha e das 3 últimas colunas de '''A''' | |||
::g) Crie uma matriz '''E''' formada pelas linhas pares e colunas múltiplas de 3 de '''A''' | |||
::h) Crie uma matriz '''F''' formada pelas linhas 1 a 7 e mais a 13 e pelas colunas 4, 5 e 1 de '''A''' | |||
:2. Assuma que a matriz '''C''' seja definida como abaixo e determine o conteúdo das seguintes submatrizes. Descubra a saída dos comandos antes de executá-los. | |||
:::<math> | |||
C = \begin{bmatrix} | |||
1{,}1 & -3{,}2 & 3{,}4 & 0{,}6 \\ | |||
0{,}6 & 1{,}1 & -0{,}6 & 3{,}1 \\ | |||
1{,}3 & 0{,}6 & 5{,}5 & 0{,}0 | |||
\end{bmatrix} | |||
</math> | |||
::a) C(2, :) | |||
::b) C(:, end) | |||
::c) C(1:2, 2:end) | |||
::d) C(6) | |||
::e) C(4:end) | |||
::f) C(1:2, 2:4) | |||
::g) C([1 3], 2) | |||
::h) C([2 2], [3 3]) | |||
:3. Determine a saída no ''command window'' após a execução dos comandos abaixo. Descubra a saída dos comandos antes de executá-los. | |||
::: A = [1 2 3; 4 5 6; 7 8 9] | |||
::: A([3 1], :) = A([1 3], :) | |||
::: A([1 3], :) = A([2 2], :) | |||
::: A = A(:, [2 2]) | |||
:4. Determine o conteúdo da matriz '''A''' após a execução das seguintes declarações. Descubra a saída dos comandos antes de executá-los. | |||
::a) A = eye(3,3); | |||
::: b = [1 2 3]; | |||
::: A(2, :) = b; | |||
::b) A = eye(3,3); | |||
::: b = [4 5 6]; | |||
::: A(:, 3) = b'; | |||
::c) A = eye(3,3); | |||
::: b = [7 8 9]; | |||
::: A(3, :) = b([3 1 2]); | |||
* Concatenação de vetores e matrizes | |||
* Comandos ''repmat'', ''reshape'', ''fliplr'' e ''flipud'' | |||
* [[FIC_MATLAB_2018-2/Aula-5|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 6 - Conjuntos; Polinômios; Texto; Entrada e saída de dados === | |||
{{collapse top| bg=lightblue | 27/Set}} | |||
* Comandos ''sort'', ''unique'' | |||
* Comandos ''union'' (<math>A \cup B</math>), ''intersect'' (<math>A \cap B</math>), ''setdiff'' (<math>A \setminus B</math>), ''setxor'' (diferença simétrica) | |||
* '''Exercícios''': | |||
:1. Mostre todos os inteiros positivos menores que 100 que são múltiplos de 3 ou de 5. | |||
:2. Mostre todos os inteiros positivos menores que 200 que são múltiplos de 3 e 5. | |||
:3. Mostre todos os inteiros positivos menores que 125 que são múltiplos de 3 ou de 5, mas não de ambos. | |||
* Polinômios | |||
:* Representação de polinômios a partir de vetores | |||
:* Comandos ''polyval'', ''poly'' e ''roots'' | |||
:* Comandos ''conv'' e ''deconv'' para multiplicação e divisão de polinômios | |||
:* Comandos ''polyder'' e ''polyint'' para derivada e integral de polinômios | |||
* '''Exercícios''': | |||
:1. Utilize o MATLAB para obter as raízes do polinômio | |||
:::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math>. | |||
::Utilize a função ''poly'' para confirmar sua resposta. | |||
:2. Utilize o MATLAB para confirmar que | |||
:::::<math>\displaystyle{(20x^3 - 7x^2 + 5x + 10)(4x^2 + 12x - 3) = 80x^5 + 212x^4 - 124x^3 + 121x^2 + 105x - 30}.</math> | |||
:3. Utilize o MATLAB para confirmar que | |||
:::::<math>\frac{12x^3 + 5x^2 - 2x + 3}{3x^2 - 7x + 4} = 4x + 11</math> | |||
::com resto de <math>\displaystyle{59x - 41}</math>. | |||
:4. Utilize o MATLAB para confirmar que | |||
:::::<math>\frac{6x^3 + 4x^2 - 5}{12x^3 - 7x^2 + 3x + 9} = 0{,}7108</math> | |||
::quando <math>x = 2</math>. | |||
:5. Plote o polinômio | |||
:::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math> | |||
::ao longo da faixa <math>-7 \leq x \leq 1</math>. | |||
* Trabalhando com texto (''string'') | |||
* Entrada/Saída de dados | |||
:* Comando ''input'' para entrada de dados | |||
:* Comando ''disp'' para saída de dados | |||
:* Comandos ''num2str'' e ''str2num'' | |||
:* Entrada de dados sem a tecla ENTER | |||
* '''Exercício''': | |||
:1. Criar uma calculadora de IMC com perguntas (''input'') para massa e altura. Use o ''disp'' para exibir o resultado de forma ''agradável'' ao usuário. | |||
* [[FIC_MATLAB_2018-2/Aula-6|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 7 - Aula de exercícios === | |||
{{collapse top| bg=lightblue | 02/Out}} | |||
* '''Exercícios''': | |||
:1. A tabela a seguir mostra o salário por hora, as horas de trabalho e a produção (número de dispositivos produzidos) em uma semana para cinco fabricantes de dispositivos. | |||
:::{| class="wikitable" | |||
! ''' ''' | |||
! '''Trabalhador 1''' | |||
! '''Trabalhador 2''' | |||
! '''Trabalhador 3''' | |||
! '''Trabalhador 4''' | |||
! '''Trabalhador 5''' | |||
|- | |||
| Salário por hora ($)|| 5,00 || 5,50 || 6,50 || 6,00 || 6,25 | |||
|- | |||
| Horas de trabalho (h) || 40 || 43 || 37 || 50 || 45 | |||
|- | |||
| Produção (dispositivos) || 1000 || 1100 || 1000 || 1200 || 1100 | |||
|} | |||
::Utilize o MATLAB para responder essas questões: | |||
:::a) Quanto cada trabalhador recebeu na semana? | |||
:::b) Qual foi o salário total pago? | |||
:::c) Quantos dispositivos foram fabricados? | |||
:::d) Qual é o custo médio para se produzir um dispositivo? | |||
:::e) Quantas horas são necessárias, em média, para se produzir um dispositivo? | |||
:::f) Assumindo que a produção de cada trabalhador tenha a mesma qualidade, qual trabalhador é o mais eficiente? Qual é o menos eficiente? | |||
:2. A aproximação de Bhaskara I para a função seno '''em graus''' é dada por: | |||
:::<math> | |||
\sin(x^{\circ}) \approx \frac{4 x (180 - x)}{40500 - x (180 - x)} ~~~ \text{para } 0 \leq x \leq 180 | |||
</math> | |||
::Crie uma figura contendo 3 plots: | |||
::* A função seno original | |||
::* A aproximação de Bhaskara I | |||
::* O erro da aproximação | |||
:3. Se uma bola é lançada da altura <math>h_0 = 28</math> m acima da superfície da terra, com velocidade vertical <math>v_0 = 20</math> m/s, a posição e a velocidade da bola como função no tempo serão dadas pelas equações | |||
:::<math>h(t) = \frac{1}{2} g t^2 + v_0 t + h_0</math> | |||
:::<math>\displaystyle{v(t) = g t + v_0}</math> | |||
::onde ''g'' é a aceleração da gravidade (-9,81 m/s²). Escreva um programa de MATLAB que desenhe a altura e a velocidade como função do tempo, utilizando o comando ''subplot''. Faça com que <math>h_0</math> e <math>v_0</math> sejam parâmetros da script. Não deixe de incluir as legendas apropriadas. | |||
:4. Joãozinho depositou <math>v_p = \text{BRL } 1.000,00</math> num fundo de investimento com taxa de juros <math>j = 0{,}8 %</math> ao mês. Faça um gráfico do saldo do investimento. Em quanto tempo o valor depositado será dobrado? Dica: [https://pt.wikipedia.org/wiki/Juro#Juros_compostos (link)] | |||
* '''Desafios''': | |||
:1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. | |||
:2. Repita o Exercício 6 da Aula 4 (Fourier) para um número de termos genérico. | |||
:3. Plote o símbolo do Batman (para quem tem dúvida, [http://guangchuangyu.github.io/blog_images/2011/08/X.png link]). | |||
* [[FIC_MATLAB_2018-2/Aula-7|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 8 - Variáveis lógicas; Operadores relacionais e lógicos === | |||
{{collapse top| bg=lightblue | 04/Out}} | |||
* Variáveis lógicas (''booleanas''): | |||
:* Comando ''logical'' | |||
* Endereçamento lógico de vetores e matrizes | |||
* Operadores: | |||
:* Operadores relacionais: | |||
:::{| class="wikitable" | |||
! '''Operador''' | |||
! '''Significado''' | |||
|- | |||
| < || Menor que | |||
|- | |||
| <= || Menor ou igual a | |||
|- | |||
| > || Maior que | |||
|- | |||
| >= || Maior ou igual a | |||
|- | |||
| == || Igual a | |||
|- | |||
| ~= || Não é igual a | |||
|} | |||
:* Operadores lógicos: | |||
:::{| class="wikitable" | |||
! '''Operador''' | |||
! '''Nome''' | |||
|- | |||
| & || AND | |||
|- | |||
| ǀ || OR | |||
|- | |||
| ~ || NOT | |||
|- | |||
| xor(a,b) || XOR | |||
|} | |||
:* Comparação de vetores ou matrizes: | |||
::* Comando ''isequal'' | |||
:* Comparação de ''strings'': | |||
::* Comandos ''strcmp'' e ''strcmpi'' | |||
* Comando ''find'' | |||
* '''Exercícios''': | |||
:1. Sejam ''x = [1 7 5 3 8 2]'' e ''y = [1 8 2 3 9 1]''. Encontre os resultados dos seguintes comandos '''antes''' de executá-los: | |||
::a) ''z = x < 6'' | |||
::b) ''z = x <= y'' | |||
::c) ''z = x == y'' | |||
::d) ''z = x ~= y'' | |||
:2. A tabela abaixo mostra as temperaturas diárias (em Celsius) em três cidades diferentes. | |||
:::{| class="wikitable" | |||
! '''Cidade \ Temperatura''' | |||
! '''Dia 1''' | |||
! '''Dia 2''' | |||
! '''Dia 3''' | |||
! '''Dia 4''' | |||
! '''Dia 5''' | |||
! '''Dia 6''' | |||
! '''Dia 7''' | |||
|- | |||
| Palhoça || 10 || 13 || 6 || 5 || -1 || 10 || 4 | |||
|- | |||
| São José || 19 || 13 || 3 || 5 || 1 || 22 || 14 | |||
|- | |||
| Biguaçu || 30 || 2 || 3 || -1 || 10 || -2 || 40 | |||
|} | |||
:Determine em quais dias: | |||
::a) A temperatura na Palhoça é maior que 8 °C. | |||
::b) A temperatura em São José se encontra entre 1 °C e 15 °C (incluindo ambos os extremos). | |||
::c) Fez mais frio na Palhoça que em São José. | |||
::d) Biguaçu foi a cidade mais quente de todas. | |||
:3. A altura e a velocidade de um projétil lançado com uma velocidade <math>v_0</math> e um ângulo com a horizontal <math>a</math> são dadas, em funcão do tempo ''t'', por | |||
:::<math>h(t) = v_0 \, t \, \mathrm{sen}(a) + \frac{1}{2} \, g \, t^2,</math> | |||
:::<math>v(t) = \sqrt{v_0^2 + 2 \, v_0 \, g \, t \, \mathrm{sen}(a) + g^2 \, t^2},</math> | |||
:respectivamente, em que ''g'' é a aceleração da gravidade. O projétil atinge o solo quando <math>h(t) = 0</math>, o que ocorre no tempo <math>t_\mathrm{hit} = -2 (v_0 / g) \mathrm{sen}(a)</math>. Suponha que <math>a = 30</math>°, <math>v_0 = 40</math> m/s e <math>g = -9{,}81</math> m/s². | |||
::a) Plote os gráficos da altura e da velocidade do projétil, de <math>t = 0</math> até <math>t = t_\mathrm{hit}</math>. | |||
::b) Determine os instantes de tempo em que a altura é de no mínimo 15 m. | |||
::c) Determine os instantes de tempo em que a altura é de no mínimo 15 m e, ao mesmo tempo, a velocidade é de no máximo 36 m/s. | |||
::d) Determine os instantes de tempo em que a altura é de no mínimo 15 m ou a velocidade é de no máximo 36 m/s. | |||
::e) Destaque as figuras anteriores com os intervalos calculados na letra c). | |||
* [[FIC_MATLAB_2018-2/Aula-8|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 9 - Controle de fluxo de dados - ''if'' e ''switch'' === | |||
{{collapse top| bg=lightblue | 09/Out}} | |||
* Controle de fluxo de dados: | |||
:* As sentenças ''if'', ''else'' e ''elseif'' | |||
* '''Exercícios''': | |||
:1. Crie um programa que recebe do usuário um número ''X''. Se este número for maior que 10, então, o programa deve mostrar o quadrado do número ''X''. Caso contrário, o número ''X'' deve ser exibido junto com uma mensagem de boa noite. | |||
:2. Escreva um programa no qual o usuário irá entrar com uma ''string'', que irá informar o assunto de uma discussão em um bate-papo da UOL. O programa deverá mostrar uma mensagem de boas vindas relacionada ao tema nos casos em que o tema seja '''cinema''', '''moda''' ou '''gastronomia'''. Se o assunto for '''politica''', '''futebol''' ou '''religiao''', o programa deverá informar que estes assuntos estão proibidos. Qualquer outro assunto é inválido, e deverá receber uma mensagem crítica. | |||
:3. Escreva um programa no qual o usuário fornece três valores: o valor inicial, o valor final e o passo de um intervalo. Crie proteções para que o intervalo seja consistente. Por exemplo, se o valor final for menor que o valor inicial, então o passo deve ser negativo. Ao fim do programa, exiba <math>x^2</math>, onde ''x'' é o intervalo. | |||
:4. Crie um código que calcula o valor gasto total (em R$) e o peso total (em kg) da compra de algumas unidades de arroz (5 kg), feijão (1 kg) e café (500 g). | |||
::* O usuário deve fornecer quantas unidades quer comprar de cada produto (comando ''input''). | |||
::* Os dados devem ser validados: verificar se o usuário forneceu alguma quantidade negativa. | |||
::* Condições de compra: | |||
:::# O preço unitário do arroz é R$15,00. Se comprar 3 ou mais, o preço cai para R$14,00 cada. | |||
:::# O preço unitário do feijão é R$12,00. Se comprar 4 ou mais, o preço cai para R$11,50 cada. | |||
:::# O preço unitário do café é R$10,00. Se comprar 3 ou mais, o preço cai para R$9,25 cada. | |||
:5. Implemente uma calculadora com as quatro operações básicas, recebendo a escolha de operação e números com o comando ''input''. Não se esqueça de implementar proteções para as entradas de dados (divisão por zero, vetores, etc). | |||
:6. Modifique o programa do cálculo do IMC de modo a informar ao usuário o grau de magreza/obesidade do indivíduo (veja [https://pt.wikipedia.org/wiki/%C3%8Dndice_de_massa_corporal#Classifica%C3%A7%C3%A3o aqui]). | |||
* A sentença ''switch'' | |||
:* Um único valor | |||
:* Múltiplos valores | |||
* '''Exercício''': | |||
:1. Reescreva o código da questão 2 anterior (bate-papo da UOL) fazendo o uso da sentença ''switch''. | |||
:2. Reescreva o código da questão 5 anterior (calculadora) fazendo o uso da sentença ''switch''. | |||
* [[FIC_MATLAB_2018-2/Aula-9|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 10 - Structs; Cells === | |||
{{collapse top| bg=lightblue | 11/Out}} | |||
* Estruturas | |||
:* Criando estruturas com o operador "." | |||
:* Criando estruturas com o comando ''struct'' | |||
:* Comando ''isfield'' para identificar se um campo existe ou não | |||
:* Comando ''rmfield'' para remover campo da estrutura | |||
* '''Exercícios:''' | |||
:1. Crie um arranjo de estruturas que contenha os os seguintes campos de informação concernentes a pontes rodoviárias em uma cidade: localização da ponte, carga máxima (toneladas), ano de construção, ano agendado para a manutenção. | |||
::a) Insira os dados abaixo na estrutura: | |||
:::{| class="wikitable" | |||
! style="font-weight: bold;" | Localização | |||
! style="font-weight: bold;" | Carga máxima | |||
! style="font-weight: bold;" | Ano de construção | |||
! style="font-weight: bold;" | Agendamento para a manutenção | |||
|- | |||
| Smith St. | |||
| 80 | |||
| 1928 | |||
| 2011 | |||
|- | |||
| Hope Ave. | |||
| 90 | |||
| 1950 | |||
| 2013 | |||
|- | |||
| Clark St. | |||
| 85 | |||
| 1933 | |||
| 2012 | |||
|- | |||
| North Rd. | |||
| 100 | |||
| 1960 | |||
| 2012 | |||
|} | |||
::b) Edite o arranjo de estruturas para mudar de 2012 para 2018 o ano agendado para a manutenção da ponte Clark St. | |||
::c) Adicione a seguinte ponte ao arranjo de estruturas: | |||
:::{| class="wikitable" | |||
! style="font-weight: bold;" | Localização | |||
! style="font-weight: bold;" | Carga máxima | |||
! style="font-weight: bold;" | Ano de construção | |||
! style="font-weight: bold;" | Agendamento para a manutenção | |||
|- | |||
| Shore Rd. | |||
| 85 | |||
| 1997 | |||
| 2014 | |||
|} | |||
:2. Crie uma estrutura que contenha todas as informações necessárias para construir um diagrama de um conjunto de dados. No mínimo, a estrutura deve conter os seguintes campos: | |||
::* '''x_data''': dado referente ao eixo "x" | |||
::* '''y_data''': dado referente ao eixo "y" | |||
::* '''title''': título do diagrama | |||
::* '''x_label''': rótulo do eixo "x" | |||
::* '''y_label''': rótulo do eixo "y" | |||
::* '''x_range''': faixa de valores exibidos no eixo "x" | |||
::* '''y_range''': faixa de valores exibidos no eixo "y" | |||
:: Você pode adicionar outros campos que aumentem seu controle sobre o diagrama final. | |||
:: Depois de criar essa estrutura, escreva um programa no MATLAB que use a estrutura para gerar um gráfico. O programa deve aplicar características iniciais inteligentes se alguns campos de dados estiverem faltando. | |||
* Arranjo de células: texto e números | |||
:* Comando ''celldisp'' e ''cellplot'' | |||
* '''Exercícios''': | |||
:1. Repita os exercícios anteriores de estruturas usando células | |||
* [[FIC_MATLAB_2018-2/Aula-10|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 11 - Estruturas de repetição - ''for'' e ''while'' === | |||
{{collapse top| bg=lightblue | 16/Out}} | |||
* Estruturas de repetição: | |||
:* Laços ''for'' | |||
:* Laços ''while'' | |||
:* Sentenças ''break'' e ''continue'' | |||
* '''Exercícios:''' | |||
:1. Acrescente à calculadora a possibilidade de continuar realizando cálculos até que o usuário solicite a saída digitando 's'. | |||
:2. Escreva um programa que calcule o fatorial de um número, utilizando ''for'' e ''while''. | |||
:3. Escreva um programa que calcule os ''n'' primeiros termos da sequência de Fibonacci, dispondo-os num vetor. | |||
:4. Considere os códigos abaixo: | |||
:::{| class="wikitable" | |||
! style="font-weight: bold;" | Símbolo | |||
! style="font-weight: bold;" | A | |||
! style="font-weight: bold;" | B | |||
! style="font-weight: bold;" | C | |||
! style="font-weight: bold;" | D | |||
! style="font-weight: bold;" | E | |||
! style="font-weight: bold;" | F | |||
|- | |||
| style="font-weight: bold;" | Código 1 | |||
| 000 | |||
| 001 | |||
| 010 | |||
| 011 | |||
| 100 | |||
| 101 | |||
|- | |||
| style="font-weight: bold;" | Código 2 | |||
| 00 | |||
| 10 | |||
| 11 | |||
| 010 | |||
| 0110 | |||
| 0111 | |||
|} | |||
::a) Escreva um programa que codifique uma sequência de símbolos, gerando a sequência de bits correspondente. Seu programa deverá funcionar tanto para o código 1 quanto para o código 2. Teste seu programa com a seguinte ''string'': F A D A B A B A C A. | |||
::b) Escreva um programa que decodifique uma ''string'' recuperando a sequência de símbolos original. Teste seu programa com a seguinte sequência de bits: | |||
::: '''Código 1''': 001000001000101100011100 | |||
::: '''Código 2''': 10001000011101100100110 | |||
::c) Junte os dois códigos anteriores num único programa, onde o usuário seleciona a operação (codificação ou decodificação), o código (1 ou 2), e entra com o dado a ser operado. | |||
:5. Escreva um programa que implementa o jogo [https://www.youtube.com/watch?v=8nOQ8mcOTLY Genius®]. O programa deverá gerar uma sequência aleatória de letras e/ou números e exibir um por um na tela, limpando-a em seguida. Após isso, aguardará o usuário entrar com a sequência. | |||
:6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função | |||
:::::<math>f(x) = | |||
\begin{cases} | |||
-1, & -\pi \leq x \leq 0 \\ | |||
1, & 0 \leq x \leq \pi | |||
\end{cases}</math> | |||
::é | |||
:::::<math>g(x) = \frac{4}{\pi} \left( \frac{\sin(x)}{1} + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5} + \frac{\sin(7x)}{7} + \cdots \right)</math>. | |||
::Plote em um mesmo gráfico a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando um número de termos definido pelo usuário. | |||
* [[FIC_MATLAB_2018-2/Aula-11|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 12 - Funções; Exercícios === | |||
{{collapse top| bg=lightblue | 18/Out}} | |||
* Funções definidas pelo usuário | |||
:* Único retorno | |||
:* Múltiplos retornos | |||
:* Comando ''return'' | |||
*'''Exercícios:''' | |||
:1. Adapte os Exercícios 2 e 3 da Aula 11 de modo a utilizar funções. | |||
:2. Escreva uma função que retorna a média aritmética e a média geométrica de dois dados números. | |||
:3. Escreva uma função que determina o tempo (em anos) necessário para que você acumule pelo menos VF (em dólares) em uma conta bancária se você depositar inicialmente V0 (em dólares) e mais P (em dólares) ao final de cada ano, com um rendimento anual de R%. | |||
:4. Fazer o ''plot'' de um sinal de tensão versus tempo, como da figura, usando os conceitos da aula de hoje. | |||
:::::<math>f(t) = | |||
\begin{cases} | |||
\sin(2 \pi t / 63), & \text{de } t = 1s \text{ ate } t = 63s \\ | |||
0, & \text{de } t = 64s \text{ ate } t = 80s \\ | |||
1, & \text{de } t = 81s \text{ ate } t = 100s \\ | |||
-1, & \text{de } t = 101s \text{ ate } t = 120s | |||
\end{cases}</math> | |||
:: Não esquecer de nomear os eixos. | |||
[[Image:Exercícios Aula 3 FIC Matlab.jpg|400px|center]] | |||
:5. Escreva uma função que implementa a [https://pt.wikipedia.org/wiki/Cifra_de_C%C3%A9sar Cifra de César]. A entrada da função deve ser: | |||
::* O ''string'' a ser codificado/decodificado; | |||
::* O deslocamento a ser aplicado em cada letra do ''string'', podendo ser um inteiro positivo (deslocamento para a direita) ou negativo (deslocamento para a esquerda). | |||
:6. Escreva uma função que retorna todos os números primos menores ou iguais a um dado inteiro ''n''. Utilize o algoritmo do [https://pt.wikipedia.org/wiki/Crivo_de_Erat%C3%B3stenes Crivo de Erastótenes]. | |||
* [[FIC_MATLAB_2018-2/Aula-12|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 13 - Processamento de imagens === | |||
{{collapse top| bg=lightblue | 23/Out}} | |||
<!--'''Pro futuro:''' Usar ''im2double''!--> | |||
[[Curso Matlab aplicado ao processamento de imagens - Aula 3]] | |||
* [[FIC_MATLAB_2018-2/Aula-13|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 14 - Importação de dados; Gráficos em 2D e 3D === | |||
{{collapse top| bg=lightblue | 25/Out}} | |||
* Importação de dados | |||
:* Comando ''uiimport'' | |||
:* Formato do separador decimal (''.'' ou '','') | |||
: Exemplo: usar [https://wiki.sj.ifsc.edu.br/images/8/84/Celular4g.txt Celular4g.txt], importar e trabalhar com as funções de matrizes. | |||
*'''Exercícios''': | |||
:1. Com o arquivo [https://wiki.sj.ifsc.edu.br/images/f/fe/Add_user.txt Add_user.txt] (Adições Líquidas de Aparelhos 4G das Operadoras no período), calcular a soma dos anos 2014, 2015 e 2016 (até o momento) por operadora e a soma e a média por período. | |||
* '''Gráficos em 2D''' | |||
:* Revisão: Comandos ''plot'', ''stem'', ''bars'' e ''stairs'' | |||
:* Comandos ''semilogx'', ''semilogy'' e ''loglog'' | |||
::* Exemplo: Resposta em frequência de um [https://en.wikipedia.org/wiki/Low-pass_filter filtro passa-baixa] de segunda ordem: | |||
:::<math>H(\omega) = \dfrac{1}{\sqrt{1 + \omega^2}}</math> | |||
:* Comando ''polar'' | |||
::* Exemplo: [https://pt.wikipedia.org/wiki/Rosa_polar Rosas polares]: | |||
::: <math>\rho = \mathrm{cos}(k \theta)</math>, onde ''k'' é um parâmetro. | |||
::* Números complexos e funções ''abs'' e ''angle'' | |||
:* Comando ''plotyy'' para plotar gráficos com dois eixos em '''y'''. | |||
:* Letras gregas nos gráficos: | |||
:::{| class="wikitable" | |||
! '''Letra''' | |||
! '''Representação''' | |||
|- | |||
| <math> \alpha </math> || \alpha | |||
|- | |||
| <math> \beta </math> || \beta | |||
|- | |||
| <math> \gamma </math> || \gamma | |||
|- | |||
| <math> \delta </math> || \delta | |||
|- | |||
| <math> \epsilon </math> || \epsilon | |||
|- | |||
| <math> \kappa </math> || \kappa | |||
|- | |||
| <math> \lambda </math> || \lambda | |||
|- | |||
| <math> \mu </math> || \mu | |||
|- | |||
| <math> \nu </math> || \nu | |||
|- | |||
| <math> \omega </math> || \omega | |||
|- | |||
| <math> \phi </math> || \phi | |||
|- | |||
| <math> \pi </math> || \pi | |||
|- | |||
| <math> \chi </math> || \chi | |||
|- | |||
| <math> \psi </math> || \psi | |||
|- | |||
| <math> \rho </math> || \rho | |||
|- | |||
| <math> \sigma </math> || \sigma | |||
|- | |||
| <math> \tau </math> || \tau | |||
|- | |||
| <math> \upsilon </math> || \upsilon | |||
|- | |||
| <math> \Sigma </math> || \Sigma | |||
|- | |||
| <math> \Pi </math> || \Pi | |||
|- | |||
| <math> \Lambda </math> || \Lambda | |||
|- | |||
| <math> \Omega </math> || \Omega | |||
|- | |||
| <math> \Gamma </math> || \Gamma | |||
|- | |||
|} | |||
<!-- | |||
Exercício (livro - adaptado - 10 p.253): Muitas aplicações utilizam a seguinte aproximação de "ângulo pequeno" para o seno com a finalidade de se obter um modelo mais simples que seja fácil de ser entendido e analisado. A aproximação estabelece que ''sen(x)'' <math>\simeq x</math>, em que ''x'' deve ser em radianos. Investigue a precisão desta aproximação com dois plots. No primeiro, plote ''sen(x) versus x'' para <math>0 \leq x \leq 1</math>. No segundo, plote o erro da aproximação ''(sen(x) - x) versus x'' para <math>0 \leq x \leq 1</math>. | |||
--> | |||
* '''Exercícios''': | |||
:1. Plote '''em vermelho''' a função polar | |||
:::<math>\rho = \dfrac{\mathrm{sen}(\theta) \sqrt{|\cos(\theta)|}} {\mathrm{sen}(\theta) + 7/5} - 2 \mathrm{sen}(\theta) + 2</math>, de <math>-\pi \leq \theta \leq \pi</math>. | |||
:2. Plote o gráfico da função <math>\sqrt{x}</math> utilizando todos os quatro tipos de combinações de eixos (linear/logarítmico). | |||
:3. As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. | |||
::: <math>\displaystyle{x(t) = 1000 e^{-0,5t} \mathrm{sen}(3t+2)}</math> | |||
::: <math>\displaystyle{y(t) = 7 e^{-0,4t} \cos(5t-3)}</math> | |||
* '''Gráficos em 3D''' | |||
:* Gráficos de linha em 3D | |||
::* Comando ''plot3'' | |||
:::* Exemplo: Equações paramétricas para uma [https://pt.wikipedia.org/wiki/H%C3%A9lice_(geometria) hélice circular]: | |||
::::: <math>x = a \cos(t)</math> | |||
::::: <math>y = a \sin(t)</math> | |||
::::: <math>z = b t </math> | |||
::* Comando ''view'' | |||
::* Rótulo no eixo z: ''zlabel'' | |||
:* Gráficos de superfície | |||
::* Comando ''meshgrid'' para criar uma malha 3D | |||
::* Comando ''surf'' para plot de função de ''f(x,y)'' | |||
:::* Comando ''shading'', com parâmetros ''flat'', ''faceted'' e ''interp'' | |||
:::* Comando alternativo ''mesh'' | |||
:::* Exemplo: Símbolo da Itapema FM incompleto: | |||
::::: [X,Y] = meshgrid(-20:0.5:20); | |||
::::: R = sqrt(X.^2 + Y.^2) + eps; | |||
::::: Z = sin(R)./R; | |||
::::: surf(X,Y,Z) | |||
:* Curva de níveis: | |||
::* Comandos ''contour'', ''surfc'' e ''meshc'' | |||
[[Arquivo:FIC_Matlab_Exercicios_plot.pdf|Exercícios]] | |||
* [[FIC_MATLAB_2018-2/Aula-14|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 15 - Solução de sistemas de equações; Toolbox simbólico === | |||
{{collapse top| bg=lightblue | 30/Out}} | |||
* Sistemas de equações lineares | |||
:* Encontrando a solução de ''Ax = b'' com ''A\b'' | |||
<!-- Talvez falar sobre a função rref - forma escalonada reduzida de linha --> | |||
::* Exemplo: Balanceamento de equações químicas | |||
:::::<math>C_3 H_8 + O_2 \longrightarrow CO_2 + H_2 O</math> | |||
:::::<math>x (C_3 H_8) + y (O_2) \longrightarrow z (C O_2) + w (H_2 O)</math> | |||
:::::<math>\begin{cases} | |||
3x = z & \text{(carbono)} \\ | |||
8x = 2w & \text{(hidrogenio)} \\ | |||
2y = 2z + w & \text{(oxigenio)} \\ | |||
x + y + z + w = 1 & \text{(normalizacao)} \\ | |||
\end{cases}</math> | |||
:::::<math>\begin{cases} | |||
3x - z = 0 \\ | |||
8x - 2w = 0 \\ | |||
2y - 2z - w = 0 \\ | |||
x + y + z + w = 1 \\ | |||
\end{cases}</math> | |||
<!-- [[Image:MATLAB_Chem_Balance.jpg|300px|center]] --> | |||
* Toolbox simbólico | |||
:* Básico | |||
::* Comandos ''syms'' e ''sym'' | |||
::* Comandos ''pretty'' e ''latex'' | |||
::* Comando ''subs'' | |||
:::* Valores via argumento da função | |||
:::* Valores retirados do workspace | |||
::* Comandos ''factor'', ''expand'', ''collect'' e ''simplify'' | |||
:* Cálculo | |||
::* Comando ''limit'': Limites | |||
:::* <math>\lim_{x \to 0} \frac{\sin(x)}{x}</math> | |||
:::* <math>\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right)^x</math> | |||
::* Comando ''diff'': Derivada primeira, segunda, terceira, etc. | |||
::* Comando ''int'': Integrais indefinidas e definidas | |||
:::* <math>\int x^a dx</math> | |||
:* Interlúdio: comandos ''assume'' e ''assumptions'' | |||
:* Mais cálculo | |||
::* Comando ''taylor'': Séries de Taylor | |||
::* Comando ''symsum'': Somatórios / séries | |||
::* Outros: ''dsolve'', ''fourier'', ''laplace'', ''partfrac'' | |||
:* Solução de equações | |||
::* Comando ''solve'' | |||
[[FIC_MATLAB_2018-2/Aula-15|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 16 - Interface gráfica === | |||
{{collapse top| bg=lightblue | 01/Nov}} | |||
[[Curso Matlab aplicado ao processamento de imagens - Aula 2|Aula]] | |||
{{collapse top| bg=lightblue | Proposta de Interface gráfica}} | |||
<code> | |||
function varargout = Interface(varargin) | |||
% INTERFACE MATLAB code for Interface.fig | |||
% INTERFACE, by itself, creates a new INTERFACE or raises the existing | |||
% singleton*. | |||
% | |||
% H = INTERFACE returns the handle to a new INTERFACE or the handle to | |||
% the existing singleton*. | |||
% | |||
% INTERFACE('CALLBACK',hObject,eventData,handles,...) calls the local | |||
% function named CALLBACK in INTERFACE.M with the given input arguments. | |||
% | |||
% INTERFACE('Property','Value',...) creates a new INTERFACE or raises the | |||
% existing singleton*. Starting from the left, property value pairs are | |||
% applied to the GUI before Interface_OpeningFcn gets called. An | |||
% unrecognized property name or invalid value makes property application | |||
% stop. All inputs are passed to Interface_OpeningFcn via varargin. | |||
% | |||
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one | |||
% instance to run (singleton)". | |||
% | |||
% See also: GUIDE, GUIDATA, GUIHANDLES | |||
% Edit the above text to modify the response to help Interface | |||
% Last Modified by GUIDE v2.5 19-Apr-2017 19:45:52 | |||
% Begin initialization code - DO NOT EDIT | |||
gui_Singleton = 1; | |||
gui_State = struct('gui_Name', mfilename, ... | |||
'gui_Singleton', gui_Singleton, ... | |||
'gui_OpeningFcn', @Interface_OpeningFcn, ... | |||
'gui_OutputFcn', @Interface_OutputFcn, ... | |||
'gui_LayoutFcn', [] , ... | |||
'gui_Callback', []); | |||
if nargin && ischar(varargin{1}) | |||
gui_State.gui_Callback = str2func(varargin{1}); | |||
end | |||
if nargout | |||
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); | |||
else | |||
gui_mainfcn(gui_State, varargin{:}); | |||
end | |||
% End initialization code - DO NOT EDIT | |||
% --- Executes just before Interface is made visible. | |||
function Interface_OpeningFcn(hObject, eventdata, handles, varargin) | |||
% This function has no output args, see OutputFcn. | |||
% hObject handle to figure | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
% varargin command line arguments to Interface (see VARARGIN) | |||
handles.contador = 0; | |||
display(handles.contador) | |||
assignin('base','handles',handles) | |||
% Choose default command line output for Interface | |||
handles.output = hObject; | |||
% Update handles structure | |||
guidata(hObject, handles); | |||
% UIWAIT makes Interface wait for user response (see UIRESUME) | |||
% uiwait(handles.figure1); | |||
% --- Outputs from this function are returned to the command line. | |||
function varargout = Interface_OutputFcn(hObject, eventdata, handles) | |||
% varargout cell array for returning output args (see VARARGOUT); | |||
% hObject handle to figure | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
% Get default command line output from handles structure | |||
varargout{1} = handles.output; | |||
% --- Executes on button press in btnDesenhar. | |||
function btnDesenhar_Callback(hObject, eventdata, handles) | |||
% hObject handle to btnDesenhar (see GCBO) | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
%Incrementa o contador | |||
handles.contador = handles.contador + 1; | |||
display(handles.contador) | |||
%handles | |||
%Axis 1 | |||
hold(handles.axes1,'off') | |||
amostras = [0:1:1000]; | |||
if not(isempty(str2num(get(handles.edtFrequencias,'String')))) | |||
Freq = str2num(get(handles.edtFrequencias,'String')) | |||
onda = 2*pi*Freq*0.001*amostras; | |||
plot(handles.axes1,sin(onda)) | |||
grid(handles.axes1,'on') | |||
assignin('base','contador',handles.contador); | |||
assignin('base','hObject',hObject) | |||
% Update handles structure | |||
guidata(hObject, handles); | |||
if (get(handles.rbtCosseno,'Value') == 1) | |||
%Axis 2 | |||
plot(handles.axes2,cos(onda)) | |||
grid(handles.axes2,'on') | |||
elseif (get(handles.rbtTangente,'Value') == 1) | |||
%Axis 2 | |||
plot(handles.axes2,tan(onda)) | |||
grid(handles.axes2,'on') | |||
ylim(handles.axes2,[-2,2]) | |||
else | |||
errordlg('Selecione uma onda de saída!') | |||
end | |||
end | |||
% --- Executes on button press in rbtCosseno. | |||
function rbtCosseno_Callback(hObject, eventdata, handles) | |||
% hObject handle to rbtCosseno (see GCBO) | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
% Hint: get(hObject,'Value') returns toggle state of rbtCosseno | |||
set(hObject,'Value',1) | |||
set(handles.rbtTangente,'Value',0) | |||
% --- Executes on button press in rbtTangente. | |||
function rbtTangente_Callback(hObject, eventdata, handles) | |||
% hObject handle to rbtTangente (see GCBO) | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
% Hint: get(hObject,'Value') returns toggle state of rbtTangente | |||
set(hObject,'Value',1) | |||
set(handles.rbtCosseno,'Value',0) | |||
function edtFrequencias_Callback(hObject, eventdata, handles) | |||
% hObject handle to edtFrequencias (see GCBO) | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles structure with handles and user data (see GUIDATA) | |||
% Hints: get(hObject,'String') returns contents of edtFrequencias as text | |||
% str2double(get(hObject,'String')) returns contents of edtFrequencias as a double | |||
% --- Executes during object creation, after setting all properties. | |||
function edtFrequencias_CreateFcn(hObject, eventdata, handles) | |||
% hObject handle to edtFrequencias (see GCBO) | |||
% eventdata reserved - to be defined in a future version of MATLAB | |||
% handles empty - handles not created until after all CreateFcns called | |||
% Hint: edit controls usually have a white background on Windows. | |||
% See ISPC and COMPUTER. | |||
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) | |||
set(hObject,'BackgroundColor','white'); | |||
end | |||
</syntaxhighlight> | |||
{{collapse bottom}} | |||
[[FIC_MATLAB_2018-2/Aula-16|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 17 - Projeto === | |||
{{collapse top| bg=lightblue | 06/Nov}} | |||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | |||
=== 18 - Projeto === | |||
{{collapse top| bg=lightblue | 08/Nov}} | |||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | |||
=== 19 - Projeto === | |||
{{collapse top| bg=lightblue | 13/Nov}} | |||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | |||
=== 20 - Projeto === | |||
{{collapse top| bg=lightblue | 15/Nov}} | |||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | {{collapse bottom}} | ||
Edição das 17h15min de 18 de setembro de 2018
1 Informações Básicas
- Código: MLB16470
- Professores: Diego da Silva de Medeiros e Roberto Wanderley da Nóbrega
- Início: 11/Set/2017
- Término: 20/Nov/2017
- Horário: Terças e quintas, das 19h às 22h
- Referência Básica: PALM, William J. Introdução ao MATLAB para engenheiros. Tradução de Tales Argolo Jesus. 3. ed. Porto Alegre: AMGH, 2013. xiv, 562, il. ISBN 9788580552041
- Referência Complementar: MORAIS, V.. VIEIRA, C. MATLAB Curso Completo. FCA, 2013. 644. ISBN 9727227058
2 Conteúdos Abordados
3 Conteúdos Abordados
3.1 1 - Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição
| 11/Set - | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Observações:
|
3.2 2 - Vetores e matrizes
| 13/Set |
|---|
|
|
3.3 3 - Operações com matrizes; Plots
| 18/Set | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.4 4 - Exercícios plot; Números aleatórios
3.5 5 - Endereçamento e concatenação de vetores e matrizes; Repmat e Reshape
| 25/Set |
|---|
|
3.6 6 - Conjuntos; Polinômios; Texto; Entrada e saída de dados
| 27/Set |
|---|
|
3.7 7 - Aula de exercícios
| 02/Out | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.8 8 - Variáveis lógicas; Operadores relacionais e lógicos
| 04/Out | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.9 9 - Controle de fluxo de dados - if e switch
| 09/Out |
|---|
|
3.10 10 - Structs; Cells
| 11/Out | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.11 11 - Estruturas de repetição - for e while
| 16/Out | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.12 12 - Funções; Exercícios
| 18/Out |
|---|
|
3.13 13 - Processamento de imagens
3.14 14 - Importação de dados; Gráficos em 2D e 3D
| 25/Out | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.15 15 - Solução de sistemas de equações; Toolbox simbólico
| 30/Out |
|---|
|
3.16 16 - Interface gráfica
| 01/Nov | ||
|---|---|---|
|
3.17 17 - Projeto
| 06/Nov |
|---|
|
Aula dedicada ao projeto. |
3.18 18 - Projeto
| 08/Nov |
|---|
|
Aula dedicada ao projeto. |
3.19 19 - Projeto
| 13/Nov |
|---|
|
Aula dedicada ao projeto. |
3.20 20 - Projeto
| 15/Nov |
|---|
|
Aula dedicada ao projeto. |
3.21 Vetores e matrizes
| 13/Set |
|---|
|
3.22 Operações com matrizes; Plots
3.23 Números aleatórios; Endereçamento de vetores e matrizes
| 20/Set |
|---|
|
3.24 Aula de exercícios
| 25/Set | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.25 Concatenação de matrizes; Polinômios; Conjuntos; Texto; Entrada e saída de dados
| 27/Set |
|---|
    
|
3.26 Variáveis lógicas; Operadores; Controle de fluxo de dados - if
| 02/Out | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.27 Controle de fluxo de dados - switch; Structs; Cells
| 04/Out | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.28 Estruturas de repetição - for e while
| 09/Out | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.29 Funções; Importação de dados; Solução de sistemas de equações
| 11/Out |
|---|


|
3.30 Processamento de imagens
| 16/Out |
|---|
|
Pro futuro: Usar im2double! |
3.31 Gráficos em 2D e 3D
| 18/Out | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
3.32 Toolbox simbólico
| 23/Out |
|---|
|
Básico
Cálculo
Solução de equações
|
3.33 Interface gráfica
| 25/Out | ||
|---|---|---|
|
3.34 Projeto
| 30/Out |
|---|
|
Aula dedicada ao projeto. |
3.35 Projeto
| 01/Nov |
|---|
|
Aula dedicada ao projeto. |
3.36 Projeto
| 06/Nov |
|---|
|
Aula dedicada ao projeto. |
| Próximos episódios |
|---|
4 Questões da turma
5 Projetos finais
5.1 Ideias
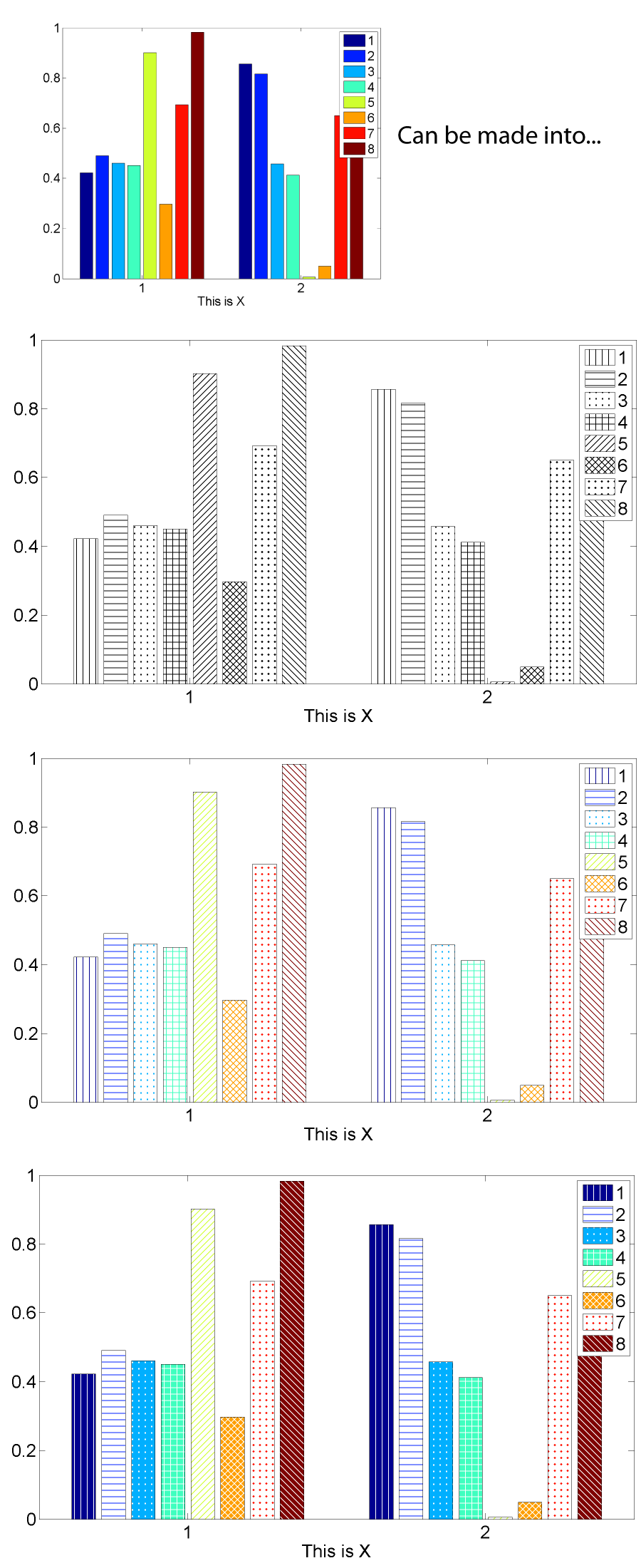
5.1.1 Hachuras em gráficos de barras
Implementar uma função em MATLAB que plote um gráfico de barras com hachuras. O comportamento deve ser semelhante ao comando bar, nativo do MATLAB, mas parâmetros poderão ser acrescentados para controle da trama. Um exemplo de resultado pode ser visto na figura abaixo:
5.1.2 Genius®
Implementar uma versão avançada do jogo Genius® construído na aula 9, adicionando sons, elementos gráficos, etc.
5.1.3 Outros
- relógio analógico
- dtmf
- sudoku
- jogo da velha
- contar moedas
- esteganografia
- batalha naval