I - Definição: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
Consideremos uma | Consideremos uma funçã<math>Inserir fórmula aqui</math>o ''y = f(x)'' definida no plano ''xy'' e vamos admitir que uma reta intercepte ''y = f(x)'' em um ponto ''P[c, f(c)]'' fixo e em um ponto <math>Q = [c + \Delta x, f(c + \Delta x)]</math>. A reta que intercepta dois pontos de uma curva é denominada ''reta secante''. A inclinação ou coeficiente angular ''m'' desta reta secante pode ser dada por | ||
<math>m = \frac{f(c + \Delta x) - f(c)}{c + \Delta x - c} = \frac{f(c + \Delta x) - f(c)}{\Delta x}.</math> | <math>m = \frac{f(c + \Delta x) - f(c)}{c + \Delta x - c} = \frac{f(c + \Delta x) - f(c)}{\Delta x}.</math> | ||
| Linha 57: | Linha 57: | ||
<math> = \lim\limits_{\Delta x\to 0} [3x^2 + 3x(\Delta x) + (\Delta x)^2 + 2] = 3x^2 + 2.</math> | <math> = \lim\limits_{\Delta x\to 0} [3x^2 + 3x(\Delta x) + (\Delta x)^2 + 2] = 3x^2 + 2.</math> | ||
<math>\frac{1}{R} | |||
<math>\frac{1}{R}\int_0^R\frac{2mL}{\sqrt{(L^2+r^2)^3}}dr</math> | |||
Edição das 15h58min de 15 de agosto de 2008
Consideremos uma funçãFalhou ao verificar gramática (erro de sintaxe): {\displaystyle Inserir fórmula aqui} o y = f(x) definida no plano xy e vamos admitir que uma reta intercepte y = f(x) em um ponto P[c, f(c)] fixo e em um ponto . A reta que intercepta dois pontos de uma curva é denominada reta secante. A inclinação ou coeficiente angular m desta reta secante pode ser dada por
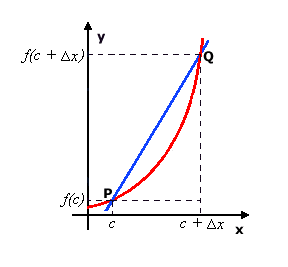
Agora, admitindo o ponto P fixo, iremos rotacionar a reta secante até que ela tangencie a curva em um único ponto, neste caso o ponto P. Ao rotacionar a reta secante, os valores de (x,y) correspondentes ao ponto Q vão se aproximando dos valores de (x,y) correspondentes ao ponto P. Esta condição limite é também aplicável ao valor da inclinação da reta secante, ou seja, à medida que Q se aproxima de P, o valor da inclinação da reta secante vai se aproximando do valor da inclinação da reta tangente.
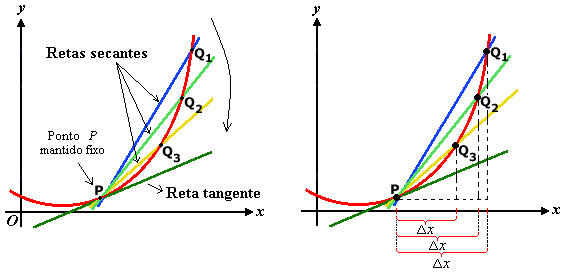
Analisando a última figura, é possível notar que à medida que a reta secante vai se aproximando da reta tangente, a porção vai assumindo valores cada vez menores, ou seja, tende a zero.
Então a inclinação da reta tangente pode ser definda pelo valor limite das inclinações das retas tangentes qunado tende a zero, ou seja,
Exemplo: Encontre o coeficiente angular da reta tangenteao gráfico de nos pontos (0,1) e (-1,2).
Solução: Aplicando a definição recém obtida e admitindo x = c, temos:
* Para o ponto (0,1):
* Para o ponto (-1,2):
Obs.: Você deve ter notado que para o ponto (-1,2) não foi preciso desenvolver todo o cálculo do limite, visto que a expressão para o coeficiente angular já tinha sido obtida para calcular o valor no ponto (0,1) - m = 2x.
Este exemplo foi aplicado a uma função não-linear, mas nada impede de esta definição ser aplicada a outros tipos de funções.
Através do cálculo do limite no exemplo dado, foi obtida a função linear f(x) = 2x que tangencia a curva em qualquer ponto no plano x,y. Dizemos que esta reta é uma função derivada da função , portanto, a definição de inclinação da reta tangente à curva em um ponto (x,y) arbitrário pode ser aplicada às funções derivadas.
Exemplo: Encontre a derivada de
Solução: