FIC MATLAB 2018-2

1 Informações Básicas

Código: MLB16470

Professores: Diego da Silva de Medeiros e Roberto Wanderley da Nóbrega

Início: 11/Set/2017

Término: 20/Nov/2017

Horário: Terças e quintas, das 19h às 22h

Referência Básica: PALM, William J. Introdução ao MATLAB para engenheiros. Tradução de Tales Argolo Jesus. 3. ed. Porto Alegre: AMGH, 2013. xiv, 562, il. ISBN 9788580552041

Referência Complementar: MORAIS, V.. VIEIRA, C. MATLAB Curso Completo. FCA, 2013. 644. ISBN 9727227058

2 Conteúdos Abordados

2.1 1 - Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição

11/Set -

MATLAB e Octave; Interface do MATLAB; Command Window; Workspace; Comando whos; Current Folder; Command History; Editor; Utilização do ponto (.) no lugar de vírgula (,) para números decimais (1,33 -> 1.33); Operadores: Operação Notação matemática Sintaxe no MATLAB Adição $a+b$ a+b Subtração $a-b$ a-b Multiplicação $ab$ a*b Divisão à direita $\frac{a}{b}$ a/b Exponenciação: $a^b$ a^b ans: Variável temporária que contém a resposta mais recente. Funções Matemáticas Função Sintaxe no MATLAB $e^x$ exp(x) $\sqrt{x}$ sqrt(x) $|x|$ abs(x) $\ln (x)$ log(x) ${\log }_{10}(x)$ log10(x) ${\log }_2(x)$ log2(x) $\cos (x)$ cos(x) $\mathrm{s}\mathrm{e}\mathrm{n}(x)$ sin(x) $\mathrm{t}\mathrm{g}(x)$ tan(x) ${\cos }^{-1}(x)$ acos(x) ${\mathrm{s}\mathrm{e}\mathrm{n}}^{-1}(x)$ asin(x) ${\mathrm{t}\mathrm{g}}^{-1}(x)$ atan(x) $\lfloor x\rfloor$ (maior inteiro $\le x$) floor(x) $\lceil x\rceil$ (menor inteiro $\ge x$) ceil(x) $\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}(x)$ (arredondamento para o inteiro maior próximo) round(x) $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(x)$ (sinal de $x$) sign(x) Observações: Utilizando d após as funções sin, cos e tan e suas inversas, faz o cálculo em graus; Utilizando h após as funções sin, cos e tan e suas inversas, tem-se suas versões hiperbólicas; Exercício: 1. Supondo $x=11,6$ e $y=-17$, calcule: $a=x+y$ $b=5(x+2y)$ $c=\frac{x^2}{y}$ $d=\frac{x+y}{e^{\frac{x}{y}}{\log }_{10}(\pi )}$ $d=5,2{\cos }^2\left(\frac{x+y}{e^{\frac{x}{y}}{\log }_{10}(\pi )}\right)$ Ajudas: Comandos help, doc e lookfor; Utilizando scripts (arquivo .m); Limpeza: Utilização do ponto e vírgula (;) para não aparecer na Command Window; Comando clear para apagar variáveis; Comando clc para apagar texto na Command Window; Constantes especiais: Comandos Descrições pi O número $\pi$. 1i,1j A unidade imaginária $\sqrt{-1}$. Inf Infinito. NaN Indica um resultado numérico indefinido. Formatos de exibição: Comando Descrição e exemplo format short Quatro dígitos decimais (padrão); 13.6745 format long 16 dígitos; 17.27484029463547 format short e Cinco dígitos (quatro decimais) mais o expoente; 6.3792e+03 format long e 16 dígitos (15 decimais) mais o expoente; 6.379243784781294e-04 format bank Dois dígitos decimais; 126.73 format + Positivo, negativo ou zero; + format rat Aproximação racional; 43/7 format compact Suprime algumas linhas em branco format loose Restabelece o modo de exibição menos compacto Códigos executados na aula

2.2 2 - Vetores e matrizes

13/Set

Definições de vetores; Definições de matrizes; Comandos length e size; Arranjo de vetores: Utilizando dois pontos (:); Definição de passo; Comandos linspace e logspace; Exercícios: 1. Crie os vetores descritos abaixo usando dois métodos diferentes: a) Início: 5, Fim: 28, com 100 elementos regularmente espaçados. b) Início: 5, Fim: 14, com passo de 0,2. c) Início: -2, Fim: 5, com 50 elementos regularmente espaçados. d) Início: 100, Fim: 12, com 100 elementos regularmente espaçados. 2. Crie os vetores descritos abaixo: a) Início: 10, Fim: 1000, com 50 elementos logaritmicamente espaçados. b) Início: 0,01, Fim: 1, com 20 elementos logaritmicamente espaçados. 3. Crie um vetor x que tenha 6 valores entre 0 e 10. Em seguida, crie uma matriz A cuja primeira linha contenha os valores 3x e segunda linha contenha os valores 5x - 20. 4. Repita o exercício anterior, substituindo a palavra linha por coluna. 5. Crie o vetor v = [2 4 8 16 32 ... 512 1024] utilizando o comando logspace. Definições de matrizes eye, zeros e ones; Usando length e size na criação de matrizes; Matriz transposta ( .' ) e matriz Hermitiana ('); Códigos executados na aula

2.3 3 - Operações com matrizes; Plots

18/Set

Operações; Soma e diferença; Produto matricial; Produto e divisão elemento a elemento; Potenciação; Funções (sin, log, etc) aplicadas a matrizes; Operações entre matrizes e escalares; Comandos sum e prod; Mínimo (min), máximo (max), média (mean) e norma (norm); Determinante (det) e inversa (inv) de uma matriz; Exercícios: 1. Defina as matrizes abaixo: $A=\left[\begin{array}{ccccc}1& 2& 3& 4& 5\\ 6& 7& 8& 9& 10\\ 11& 12& 13& 14& 15\\ 16& 17& 18& 19& 20\end{array}\right]B=\left[\begin{array}{cc}1/2& 1/3\\ 1/4& 1/5\\ 1/6& 1/7\\ 1/8& 1/9\end{array}\right]C=\left[\begin{array}{cc}-1/12& 1/-3\\ 0& 0\\ 1& 17\\ 2& 19\end{array}\right]D=\left[\begin{array}{c}\sqrt{2}\\ \pi \\ e\\ \sqrt{3}\\ 42\end{array}\right]$ 2. Para as matrizes acima, realize as operações abaixo: a) B + C b) A D (multiplicação matricial) c) C BT A d) X = BT C e) X2 f) B C (multiplicação elemento a elemento) 3. Crie o vetor v = [1 4 9 16 25 ... 81 100]. 4. Crie o vetor v = [2 4 8 16 32 ... 512 1024] sem utilizar o comando logspace. 5. Utilize o MATLAB para calcular 12! (isto é, o fatorial do número 12), sem utilizar o comando factorial. 6. O número harmônico $H_n$ é definido como sendo a soma 1 + 1/2 + ... + 1/n. Utilize o MATLAB para calcular $H_{100}$. Resposta: 5.1874. 7. Seja $x=1+1/4+1/9+1/16+1/25+\cdots +1/10000^2.$ Calcule x. Em seguida, calcule $\sqrt{6x}$. Resposta: Aproximadamente $\pi$. Plots: Comandos plot, stem, bar e stairs de uma função Uso de apenas um parâmetro Comando hold para manter a curva no gráfico Comando grid para mostrar linhas em forma de grade Nomes aos eixos com xlabel e ylabel Comando title Comandos axis, xlim e ylim para ajuste de eixos Comando legend Especificadores de linha, cores e marcadores: Tipo de linha Símbolo Sólida (padrão) - Tracejada -- Tracejada com pontos -. Com pontos : Cores Símbolo Preto k Azul b Ciano c Verde g Magenta m Vermelho r Branco w Amarelo y Marcadores de dados Símbolo Ponto . Asterisco * Cruz x Círculo o Adição + Quadrado s Losango d Triângulo apontando pra cima ^ Triângulo apontando pra baixo v Triângulo apontando pra direita > Triângulo apontando pra esquerda < Estrela de 5 pontas p Estrela de 6 pontas h Outros comandos relacionados a plotagem: Comando figure Comando subplot Comando close all para fechar todas figuras Códigos executados na aula

2.4 4 - Aula de exercícios

20/Set

Exercícios (Plots) 1. Plote, em um mesmo gráfico, as funções $f(x)=\sqrt{1-(|x|-1{)}^2}$ e $g(x)=\arccos (1-|x|)-\pi ,$ para $-2\le x\le 2$. 2. Plote a função $f(x)=x^2+x-2$ de -4 até 4 e encontrar as raízes por Bhaskara. 3. Utilize o MATLAB para plotar a função $T=3\ln (2t)-5e^{0,5t}$ ao longo do intervalo $1\le t\le 3$. Insira um título na plotagem e rotule adequadamente os eixos. A variável T representa a temperatura em graus Celsius; a variável t representa o tempo em minutos. 4. Plote as funções $u=100{\log }_{10}(60x+1)$ e $v=50\cos (6x)\mathrm{s}\mathrm{e}\mathrm{n}(2x)+150x$ ao longo do intervalo $0\le x\le 2$. Rotule adequadamente a plotagem e cada uma das curvas, utilizando legend. A variável u representa a velocidade de uma Ferrari em km/h. A variável v representa a velocidade de um Fusca. 5. Use a função stem para plotar os sinais abaixo na mesma figura: $\cos (x)$, para $0\le x\le 2\pi$ $0,5\sin (x)$, para $\pi \le x\le 3\pi$ 6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função $f(x)=\{\begin{array}{ll}-1,& -\pi \le x\le 0\\ 1,& 0\le x\le \pi \end{array}$ é $g(x)=\frac{4}{\pi }(\frac{\sin (x)}{1}+\frac{\sin (3x)}{3}+\frac{\sin (5x)}{5}+\frac{\sin (7x)}{7}+\cdots )$. Plote, em um mesmo gráfico, a função f(x) e sua representação em série g(x), utilizando os quatro termos explicitados. Considere x na faixa de $-\pi$ até $\pi$. 7. Fazer o plot de um sinal de tensão versus tempo, como da figura: $f(t)=\{\begin{array}{ll}\sin (2\pi t/63),& \text{de }t=1s\text{ ate }t=63s\\ 0,& \text{de }t=64s\text{ ate }t=80s\\ 1,& \text{de }t=81s\text{ ate }t=100s\\ -1,& \text{de }t=101s\text{ ate }t=120s\end{array}$ Não esquecer de nomear os eixos. Gabarito

2.5 5 - Endereçamento de vetores e matrizes

25/Set
Endereçamento de vetores e matrizes Indexação de um elemento Índice Subscrito Submatrizes Índice Subscrito Palavra-chave end Indexação/submatrizes do lado esquerdo vs do lado direito Exclusão de linha ou coluna Códigos executados na aula

2.6 6 - Concatenação de matrizes; Texto; Entrada e saída de dados; Conjuntos; Polinômios; Números aleatórios

27/Set

Concatenação de vetores e matrizes Comandos repmat, reshape, fliplr e flipud Trabalhando com texto (string) Entrada/Saída de dados Comando input para entrada de dados Comando disp para saída de dados Comandos num2str e str2num Entrada de dados sem a tecla ENTER Exercício: 1. Criar uma calculadora de IMC com perguntas (input) para massa e altura. Use o disp para exibir o resultado de forma agradável ao usuário. Conjuntos Comandos sort, unique Comandos union ($A\cup B$), intersect ($A\cap B$), setdiff ($A\setminus B$), setxor (diferença simétrica) Polinômios Representação de polinômios a partir de vetores Comandos polyval, poly e roots Comandos conv e deconv para multiplicação e divisão de polinômios Comandos polyder e polyint para derivada e integral de polinômios Números aleatórios Comando randi para valores inteiros uniformemente distribuídos Comando rand para valores uniformemente distribuídos Comando randn para valores normalmente distribuídos Comando hist para cálculo/visualização do histograma Exercícios: 1. Mostre todos os inteiros positivos a) menores que 100 que são múltiplos de 3 ou de 5. b) menores que 200 que são múltiplos de 3 e 5. c) menores que 125 que são múltiplos de 3 ou de 5, mas não de ambos. 2. Utilize o MATLAB para obter as raízes do polinômio $x^3+13x^2+52x+6$. Utilize a função poly para confirmar sua resposta. 3. Utilize o MATLAB para confirmar que $(20x^3-7x^2+5x+10)(4x^2+12x-3)=80x^5+212x^4-124x^3+121x^2+105x-30.$ 4. Utilize o MATLAB para confirmar que $\frac{12x^3+5x^2-2x+3}{3x^2-7x+4}=4x+11$ com resto de $59x-41$. 5. Utilize o MATLAB para confirmar que $\frac{6x^3+4x^2-5}{12x^3-7x^2+3x+9}=0,7108$ quando $x=2$. 6. Plote o polinômio $x^3+13x^2+52x+6$ ao longo da faixa $-7\le x\le 1$. Códigos executados na aula

2.7 7 - Aula de exercícios

02/Out

Exercícios (endereçamento): 1. Crie uma matriz A de tamanho 15 x 15 de inteiros. a) Extraia o elemento da segunda linha e quarta coluna de A, armazenando na variável u b) Crie um vetor v formado pelos elementos da segunda coluna de A c) Crie um vetor w formado pelos elementos da última linha de A d) Crie uma matriz B formada pelos elementos da segunda até a décima coluna de A e) Crie uma matriz C formada pelos elementos da quinta até a penúltima linha de A f) Crie uma matriz D formada pelos elementos da sétima até a penúltima linha e das 3 últimas colunas de A g) Crie uma matriz E formada pelas linhas pares e colunas múltiplas de 3 de A h) Crie uma matriz F formada pelas linhas 1 a 7 e mais a 13 e pelas colunas 4, 5 e 1 de A 2. Assuma que a matriz C seja definida como abaixo e determine o conteúdo das seguintes submatrizes. Descubra a saída dos comandos antes de executá-los. $C=\left[\begin{array}{cccc}1,1& -3,2& 3,4& 0,6\\ 0,6& 1,1& -0,6& 3,1\\ 1,3& 0,6& 5,5& 0,0\end{array}\right]$ a) C(2, :) b) C(:, end) c) C(1:2, 2:end) d) C(6) e) C(4:end) f) C(1:2, 2:4) g) C([1 3], 2) h) C([2 2], [3 3]) 3. Determine a saída no command window após a execução dos comandos abaixo. Descubra a saída dos comandos antes de executá-los. A = [1 2 3; 4 5 6; 7 8 9] A([3 1], :) = A([1 3], :) A([1 3], :) = A([2 2], :) A = A(:, [2 2]) 4. Determine o conteúdo da matriz A após a execução das seguintes declarações. Descubra a saída dos comandos antes de executá-los. a) A = eye(3,3); b = [1 2 3]; A(2, :) = b; b) A = eye(3,3); b = [4 5 6]; A(:, 3) = b'; c) A = eye(3,3); b = [7 8 9]; A(3, :) = b([3 1 2]); Exercícios: 1. A tabela a seguir mostra o salário por hora, as horas de trabalho e a produção (número de dispositivos produzidos) em uma semana para cinco fabricantes de dispositivos. Trabalhador 1 Trabalhador 2 Trabalhador 3 Trabalhador 4 Trabalhador 5 Salário por hora ($) 5,00 5,50 6,50 6,00 6,25 Horas de trabalho (h) 40 43 37 50 45 Produção (dispositivos) 1000 1100 1000 1200 1100 Utilize o MATLAB para responder essas questões: a) Quanto cada trabalhador recebeu na semana? b) Qual foi o salário total pago na semana? c) Quantos dispositivos foram fabricados na semana? d) Qual é o custo médio para se produzir um dispositivo? e) Quantas horas são necessárias, em média, para se produzir um dispositivo? f) Assumindo que a produção de cada trabalhador tenha a mesma qualidade, qual trabalhador é o mais eficiente? Qual é o menos eficiente? 2. A aproximação de Bhaskara I para a função seno em graus é dada por: $\sin (x^{\circ })\approx \frac{4x(180-x)}{40500-x(180-x)}\text{para }0\le x\le 180$ Crie uma figura contendo 3 plots: A função seno verdadeira A aproximação de Bhaskara I O erro da aproximação 3. Se uma bola é lançada da altura $h_0=28$ m acima da superfície da terra, com velocidade vertical $v_0=20$ m/s, a posição e a velocidade da bola como função no tempo serão dadas pelas equações $h(t)=\frac{1}{2}g{t}^2+v_{0}t+h_0$ $v(t)=gt+v_0$ onde g é a aceleração da gravidade (-9,81 m/s²). A bola atingirá o solo em $t_{\mathrm{h}\mathrm{i}\mathrm{t}}=-\frac{v_0+\sqrt{v_0^2-2g{h}_0}}{g}.$ Escreva um programa de MATLAB que desenhe a altura e a velocidade como função do tempo, para $0\le t\le t_{\mathrm{h}\mathrm{i}\mathrm{t}}$ utilizando o comando subplot. Faça com que $h_0$ e $v_0$ sejam parâmetros da script. Não deixe de incluir as legendas apropriadas. 4. Joãozinho depositou $v_p=\text{BRL }1.000,00$ num fundo de investimento com taxa de juros $j=0,8\mathrm{\%}$ ao mês. Faça um gráfico do saldo do investimento. Em quanto tempo o valor depositado será dobrado? Dica: (link) Desafios: 1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. 2. Repita o Exercício 6 da Aula 4 com um número genérico de termos $\sin ()$ somados em $g(x)$. 3. Plote o símbolo do Batman (para quem tem dúvida, link). Códigos executados na aula

2.8 8 - Variáveis lógicas; Operadores relacionais e lógicos

04/Out

Variáveis lógicas (booleanas): Comando logical Endereçamento lógico de vetores e matrizes Operadores: Operadores relacionais: Operador Significado < Menor que <= Menor ou igual a > Maior que >= Maior ou igual a == Igual a ~= Não é igual a Operadores lógicos: Operador Nome & AND ǀ OR ~ NOT xor(a,b) XOR Comparação de vetores ou matrizes: Comando isequal Comparação de strings: Comandos strcmp e strcmpi Comando find Exercícios: 1. Sejam x = [1 7 5 3 8 2] e y = [1 8 2 3 9 1]. Encontre os resultados dos seguintes comandos antes de executá-los: a) z = x < 6 b) z = x <= y c) z = x == y d) z = x ~= y 2. A tabela abaixo mostra as temperaturas diárias (em Celsius) em três cidades diferentes. Temperatura Cidade Dia 1 Dia 2 Dia 3 Dia 4 Dia 5 Dia 6 Dia 7 Palhoça 10 13 6 5 -1 10 4 São José 19 13 3 5 1 22 14 Biguaçu 30 2 3 -1 10 -2 40 Determine em quais dias: a) A temperatura na Palhoça é maior que 8 °C. b) A temperatura em São José se encontra entre 1 °C e 15 °C (incluindo ambos os extremos). c) Fez mais frio na Palhoça que em São José. d) Biguaçu foi a cidade mais quente de todas. 3. A altura e a velocidade de um projétil lançado com uma velocidade $v_0$ e um ângulo com a horizontal $a$ são dadas, em funcão do tempo t, por $h(t)=v_{0}t\mathrm{s}\mathrm{e}\mathrm{n}(a)+\frac{1}{2}g{t}^2,$ $v(t)=\sqrt{v_0^2+2v_{0}gt\mathrm{s}\mathrm{e}\mathrm{n}(a)+g^2{t}^2},$ respectivamente, em que g é a aceleração da gravidade. O projétil atinge o solo quando $h(t)=0$, o que ocorre no tempo $t_{\mathrm{h}\mathrm{i}\mathrm{t}}=-2(v_0/g)\mathrm{s}\mathrm{e}\mathrm{n}(a)$. Suponha que $a=30$°, $v_0=40$ m/s e $g=-9,81$ m/s². a) Plote os gráficos da altura e da velocidade do projétil, de $t=0$ até $t=t_{\mathrm{h}\mathrm{i}\mathrm{t}}$. b) Determine os instantes de tempo em que a altura é de no mínimo 15 m. c) Determine os instantes de tempo em que a altura é de no mínimo 15 m e, ao mesmo tempo, a velocidade é de no máximo 36 m/s. d) Determine os instantes de tempo em que a altura é de no mínimo 15 m ou a velocidade é de no máximo 36 m/s. e) Destaque as figuras anteriores com os intervalos calculados na letra c). Códigos executados em sala

2.9 9 - Controle de fluxo de dados - if e switch

09/Out

Controle de fluxo de dados: As sentenças if, else e elseif Exercícios: 1. Crie um programa que recebe do usuário um número X. Se este número for maior que 10, então, o programa deve mostrar o quadrado do número X. Caso contrário, o número X deve ser exibido junto com uma mensagem de boa noite. 2. Escreva um programa no qual o usuário irá entrar com uma string, que irá informar o assunto de uma discussão em um bate-papo da UOL. O programa deverá mostrar uma mensagem de boas vindas relacionada ao tema nos casos em que o tema seja cinema, moda ou gastronomia. Se o assunto for politica, futebol ou religiao, o programa deverá informar que estes assuntos estão proibidos. Qualquer outro assunto é inválido, e deverá receber uma mensagem crítica. 3. Escreva um programa no qual o usuário fornece três valores: o valor inicial, o valor final e o passo de um intervalo. Crie proteções para que o intervalo seja consistente. Por exemplo, se o valor final for menor que o valor inicial, então o passo deve ser negativo. Ao fim do programa, exiba $x^2$, onde x é o intervalo. 4. Crie um código que calcula o valor gasto total (em R$) e o peso total (em kg) da compra de algumas unidades de arroz (5 kg), feijão (1 kg) e café (500 g). O usuário deve fornecer quantas unidades quer comprar de cada produto (comando input). Os dados devem ser validados: verificar se o usuário forneceu alguma quantidade negativa. Condições de compra: O preço unitário do arroz é R$15,00. Se comprar 3 ou mais, o preço cai para R$14,00 cada. O preço unitário do feijão é R$12,00. Se comprar 4 ou mais, o preço cai para R$11,50 cada. O preço unitário do café é R$10,00. Se comprar 3 ou mais, o preço cai para R$9,25 cada. 5. Implemente uma calculadora com as quatro operações básicas, recebendo a escolha de operação e números com o comando input. Não se esqueça de implementar proteções para as entradas de dados (divisão por zero, vetores, etc). 6. Modifique o programa do cálculo do IMC de modo a informar ao usuário o grau de magreza/obesidade do indivíduo (veja aqui). A sentença switch Um único valor Múltiplos valores Exercício: 1. Reescreva o código da questão 2 anterior (bate-papo da UOL) fazendo o uso da sentença switch. 2. Reescreva o código da questão 5 anterior (calculadora) fazendo o uso da sentença switch. Códigos executados em sala

2.10 10 - Structs; Cells

11/Out

Estruturas Criando estruturas com o operador "." Criando estruturas com o comando struct Comando isfield para identificar se um campo existe ou não Comando rmfield para remover campo da estrutura Exercícios: 1. Crie um arranjo de estruturas que contenha os os seguintes campos de informação concernentes a pontes rodoviárias em uma cidade: localização da ponte, carga máxima (toneladas), ano de construção, ano agendado para a manutenção. a) Insira os dados abaixo na estrutura: Localização Carga máxima Ano de construção Agendamento para a manutenção Smith St. 80 1928 2011 Hope Ave. 90 1950 2013 Clark St. 85 1933 2012 North Rd. 100 1960 2012 b) Edite o arranjo de estruturas para mudar de 2012 para 2018 o ano agendado para a manutenção da ponte Clark St. c) Adicione a seguinte ponte ao arranjo de estruturas: Localização Carga máxima Ano de construção Agendamento para a manutenção Shore Rd. 85 1997 2014 2. Crie uma estrutura que contenha todas as informações necessárias para construir um diagrama de um conjunto de dados. No mínimo, a estrutura deve conter os seguintes campos: x_data: dado referente ao eixo "x" y_data: dado referente ao eixo "y" title: título do diagrama x_label: rótulo do eixo "x" y_label: rótulo do eixo "y" x_range: faixa de valores exibidos no eixo "x" y_range: faixa de valores exibidos no eixo "y" Você pode adicionar outros campos que aumentem seu controle sobre o diagrama final. Depois de criar essa estrutura, escreva um programa no MATLAB que use a estrutura para gerar um gráfico. O programa deve aplicar características iniciais inteligentes se alguns campos de dados estiverem faltando. Arranjo de células: texto e números Comando celldisp e cellplot Exercícios: 1. Repita os exercícios anteriores de estruturas usando células Códigos executados em sala

2.11 11 - Estruturas de repetição - for e while

16/Out

Estruturas de repetição: Laços for Laços while Sentenças break e continue Exercícios: 1. Acrescente à calculadora a possibilidade de continuar realizando cálculos até que o usuário solicite a saída digitando 's'. 2. Escreva um programa que calcule o fatorial de um número, utilizando for e while. 3. Escreva um programa que calcule os n primeiros termos da sequência de Fibonacci, dispondo-os num vetor. 4. Considere os códigos abaixo: Símbolo A B C D E F Código 1 000 001 010 011 100 101 Código 2 00 10 11 010 0110 0111 a) Escreva um programa que codifique uma sequência de símbolos, gerando a sequência de bits correspondente. Seu programa deverá funcionar tanto para o código 1 quanto para o código 2. Teste seu programa com a seguinte string: F A D A B A B A C A. b) Escreva um programa que decodifique uma string recuperando a sequência de símbolos original. Teste seu programa com a seguinte sequência de bits: Código 1: 001000001000101100011100 Código 2: 10001000011101100100110 c) Junte os dois códigos anteriores num único programa, onde o usuário seleciona a operação (codificação ou decodificação), o código (1 ou 2), e entra com o dado a ser operado. 5. Escreva um programa que implementa o jogo Genius®. O programa deverá gerar uma sequência aleatória de letras e/ou números e exibir um por um na tela, limpando-a em seguida. Após isso, aguardará o usuário entrar com a sequência. 6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função $f(x)=\{\begin{array}{ll}-1,& -\pi \le x\le 0\\ 1,& 0\le x\le \pi \end{array}$ é $g(x)=\frac{4}{\pi }(\frac{\sin (x)}{1}+\frac{\sin (3x)}{3}+\frac{\sin (5x)}{5}+\frac{\sin (7x)}{7}+\cdots )$. Plote em um mesmo gráfico a função f(x) e sua representação em série g(x), utilizando um número de termos definido pelo usuário. Códigos executados em sala

2.12 12 - Funções; Exercícios

18/Out

Funções definidas pelo usuário Único retorno Múltiplos retornos Comando return Exercícios: 1. Adapte os Exercícios 2 e 3 da Aula 11 de modo a utilizar funções. 2. Escreva uma função que retorna a média aritmética e a média geométrica de dois dados números. 3. Escreva uma função que determina o tempo (em anos) necessário para que você acumule pelo menos VF (em dólares) em uma conta bancária se você depositar inicialmente V0 (em dólares) e mais P (em dólares) ao final de cada ano, com um rendimento anual de R%. 4. Fazer o plot de um sinal de tensão versus tempo, como da figura, usando os conceitos da aula de hoje. $f(t)=\{\begin{array}{ll}\sin (2\pi t/63),& \text{de }t=1s\text{ ate }t=63s\\ 0,& \text{de }t=64s\text{ ate }t=80s\\ 1,& \text{de }t=81s\text{ ate }t=100s\\ -1,& \text{de }t=101s\text{ ate }t=120s\end{array}$ Não esquecer de nomear os eixos. 5. Escreva uma função que implementa a Cifra de César. A entrada da função deve ser: O string a ser codificado/decodificado; O deslocamento a ser aplicado em cada letra do string, podendo ser um inteiro positivo (deslocamento para a direita) ou negativo (deslocamento para a esquerda). 6. Escreva uma função que retorna todos os números primos menores ou iguais a um dado inteiro n. Utilize o algoritmo do Crivo de Erastótenes. Códigos executados em sala

2.13 13 - Processamento de imagens

23/Out
Curso Matlab aplicado ao processamento de imagens - Aula 3 Códigos executados na aula

2.14 14 - Importação de dados; Gráficos em 2D e 3D

25/Out

Importação de dados Comando uiimport Formato do separador decimal (. ou ,) Exemplo: usar Celular4g‎.txt, importar e trabalhar com as funções de matrizes. Exercícios: 1. Com o arquivo Add_user.txt (Adições Líquidas de Aparelhos 4G das Operadoras no período), calcular a soma dos anos 2014, 2015 e 2016 (até o momento) por operadora e a soma e a média por período. Gráficos em 2D Revisão: Comandos plot, stem, bars e stairs Comandos semilogx, semilogy e loglog Exemplo: Resposta em frequência de um filtro passa-baixa de segunda ordem: $H(\omega )=\frac{1}{\sqrt{1+{\omega }^2}}$ Comando polar Exemplo: Rosas polares: $\rho =\mathrm{c}\mathrm{o}\mathrm{s}(k\theta )$, onde k é um parâmetro. Números complexos e funções abs e angle Comando plotyy para plotar gráficos com dois eixos em y. Letras gregas nos gráficos: Letra Representação $\alpha$ \alpha $\beta$ \beta $\gamma$ \gamma $\delta$ \delta $ϵ$ \epsilon $\kappa$ \kappa $\lambda$ \lambda $\mu$ \mu $\nu$ \nu $\omega$ \omega $\varphi$ \phi $\pi$ \pi $\chi$ \chi $\psi$ \psi $\rho$ \rho $\sigma$ \sigma $\tau$ \tau $\upsilon$ \upsilon $\mathrm{\Sigma }$ \Sigma $\mathrm{\Pi }$ \Pi $\mathrm{\Lambda }$ \Lambda $\mathrm{\Omega }$ \Omega $\mathrm{\Gamma }$ \Gamma Exercícios: 1. Plote em vermelho a função polar $\rho =\frac{\mathrm{s}\mathrm{e}\mathrm{n}(\theta )\sqrt{|\cos (\theta )|}}{\mathrm{s}\mathrm{e}\mathrm{n}(\theta )+7/5}-2\mathrm{s}\mathrm{e}\mathrm{n}(\theta )+2$, de $-\pi \le \theta \le \pi$. 2. Plote o gráfico da função $\sqrt{x}$ utilizando todos os quatro tipos de combinações de eixos (linear/logarítmico). 3. As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. $x(t)=1000e^{-0,5t}\mathrm{s}\mathrm{e}\mathrm{n}(3t+2)$ $y(t)=7e^{-0,4t}\cos (5t-3)$ Gráficos em 3D Gráficos de linha em 3D Comando plot3 Exemplo: Equações paramétricas para uma hélice circular: $x=a\cos (t)$ $y=a\sin (t)$ $z=bt$ Comando view Rótulo no eixo z: zlabel Gráficos de superfície Comando meshgrid para criar uma malha 3D Comando surf para plot de função de f(x,y) Comando shading, com parâmetros flat, faceted e interp Comando alternativo mesh Exemplo: Símbolo da Itapema FM incompleto: [X,Y] = meshgrid(-20:0.5:20); R = sqrt(X.^2 + Y.^2) + eps; Z = sin(R)./R; surf(X,Y,Z) Curva de níveis: Comandos contour, surfc e meshc Arquivo:FIC Matlab Exercicios plot.pdf Códigos executados em sala

2.15 15 - Solução de sistemas de equações; Toolbox simbólico

30/Out

Sistemas de equações lineares Encontrando a solução de Ax = b com A\b Exemplo: Balanceamento de equações químicas $C_3{H}_8+O_2⟶C{O}_2+H_{2}O$ $x(C_3{H}_8)+y(O_2)⟶z(C{O}_2)+w(H_{2}O)$ $\{\begin{array}{ll}3x=z& \text{(carbono)}\\ 8x=2w& \text{(hidrogenio)}\\ 2y=2z+w& \text{(oxigenio)}\\ x+y+z+w=1& \text{(normalizacao)}\\ \end{array}$ $\{\begin{array}{l}3x-z=0\\ 8x-2w=0\\ 2y-2z-w=0\\ x+y+z+w=1\\ \end{array}$ Toolbox simbólico Básico Comandos syms e sym Comandos pretty e latex Comando subs Valores via argumento da função Valores retirados do workspace Comandos factor, expand, collect e simplify Cálculo Comando limit: Limites $\underset{x\to 0}{\lim }\frac{\sin (x)}{x}$ $\underset{x\to \mathrm{\infty }}{\lim }{(1+\frac{1}{x})}^x$ Comando diff: Derivada primeira, segunda, terceira, etc. Comando int: Integrais indefinidas e definidas $\int x^{a}dx$ Interlúdio: comandos assume e assumptions Mais cálculo Comando taylor: Séries de Taylor Comando symsum: Somatórios / séries Outros: dsolve, fourier, laplace, partfrac Solução de equações Comando solve Códigos executados em sala

2.16 16 - Interface gráfica

01/Nov

Aula Proposta de Interface gráfica function varargout = Interface(varargin) % INTERFACE MATLAB code for Interface.fig % INTERFACE, by itself, creates a new INTERFACE or raises the existing % singleton*. % % H = INTERFACE returns the handle to a new INTERFACE or the handle to % the existing singleton*. % % INTERFACE('CALLBACK',hObject,eventData,handles,...) calls the local % function named CALLBACK in INTERFACE.M with the given input arguments. % % INTERFACE('Property','Value',...) creates a new INTERFACE or raises the % existing singleton*. Starting from the left, property value pairs are % applied to the GUI before Interface_OpeningFcn gets called. An % unrecognized property name or invalid value makes property application % stop. All inputs are passed to Interface_OpeningFcn via varargin. % % *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one % instance to run (singleton)". % % See also: GUIDE, GUIDATA, GUIHANDLES % Edit the above text to modify the response to help Interface % Last Modified by GUIDE v2.5 19-Apr-2017 19:45:52 % Begin initialization code - DO NOT EDIT gui_Singleton = 1; gui_State = struct('gui_Name', mfilename, ... 'gui_Singleton', gui_Singleton, ... 'gui_OpeningFcn', @Interface_OpeningFcn, ... 'gui_OutputFcn', @Interface_OutputFcn, ... 'gui_LayoutFcn', [] , ... 'gui_Callback', []); if nargin && ischar(varargin{1}) gui_State.gui_Callback = str2func(varargin{1}); end if nargout [varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); else gui_mainfcn(gui_State, varargin{:}); end % End initialization code - DO NOT EDIT % --- Executes just before Interface is made visible. function Interface_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to Interface (see VARARGIN) handles.contador = 0; display(handles.contador) assignin('base','handles',handles) % Choose default command line output for Interface handles.output = hObject; % Update handles structure guidata(hObject, handles); % UIWAIT makes Interface wait for user response (see UIRESUME) % uiwait(handles.figure1); % --- Outputs from this function are returned to the command line. function varargout = Interface_OutputFcn(hObject, eventdata, handles) % varargout cell array for returning output args (see VARARGOUT); % hObject handle to figure % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Get default command line output from handles structure varargout{1} = handles.output; % --- Executes on button press in btnDesenhar. function btnDesenhar_Callback(hObject, eventdata, handles) % hObject handle to btnDesenhar (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) %Incrementa o contador handles.contador = handles.contador + 1; display(handles.contador) %handles %Axis 1 hold(handles.axes1,'off') amostras = [0:1:1000]; if not(isempty(str2num(get(handles.edtFrequencias,'String')))) Freq = str2num(get(handles.edtFrequencias,'String')) onda = 2*pi*Freq*0.001*amostras; plot(handles.axes1,sin(onda)) grid(handles.axes1,'on') assignin('base','contador',handles.contador); assignin('base','hObject',hObject)  % Update handles structure guidata(hObject, handles); if (get(handles.rbtCosseno,'Value') == 1) %Axis 2 plot(handles.axes2,cos(onda)) grid(handles.axes2,'on') elseif (get(handles.rbtTangente,'Value') == 1) %Axis 2 plot(handles.axes2,tan(onda)) grid(handles.axes2,'on') ylim(handles.axes2,[-2,2]) else errordlg('Selecione uma onda de saída!') end end % --- Executes on button press in rbtCosseno. function rbtCosseno_Callback(hObject, eventdata, handles) % hObject handle to rbtCosseno (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Hint: get(hObject,'Value') returns toggle state of rbtCosseno set(hObject,'Value',1) set(handles.rbtTangente,'Value',0) % --- Executes on button press in rbtTangente. function rbtTangente_Callback(hObject, eventdata, handles) % hObject handle to rbtTangente (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Hint: get(hObject,'Value') returns toggle state of rbtTangente set(hObject,'Value',1) set(handles.rbtCosseno,'Value',0) function edtFrequencias_Callback(hObject, eventdata, handles) % hObject handle to edtFrequencias (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Hints: get(hObject,'String') returns contents of edtFrequencias as text % str2double(get(hObject,'String')) returns contents of edtFrequencias as a double % --- Executes during object creation, after setting all properties. function edtFrequencias_CreateFcn(hObject, eventdata, handles) % hObject handle to edtFrequencias (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles empty - handles not created until after all CreateFcns called % Hint: edit controls usually have a white background on Windows. % See ISPC and COMPUTER. if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor')) set(hObject,'BackgroundColor','white'); end </syntaxhighlight> Códigos executados em sala

2.17 17 - Projeto

06/Nov
Aula dedicada ao projeto.

2.18 18 - Projeto

08/Nov
Aula dedicada ao projeto.

2.19 19 - Projeto

13/Nov
Aula dedicada ao projeto.

2.20 20 - Projeto

15/Nov
Aula dedicada ao projeto.

4 Projetos finais

4.1 Ideias

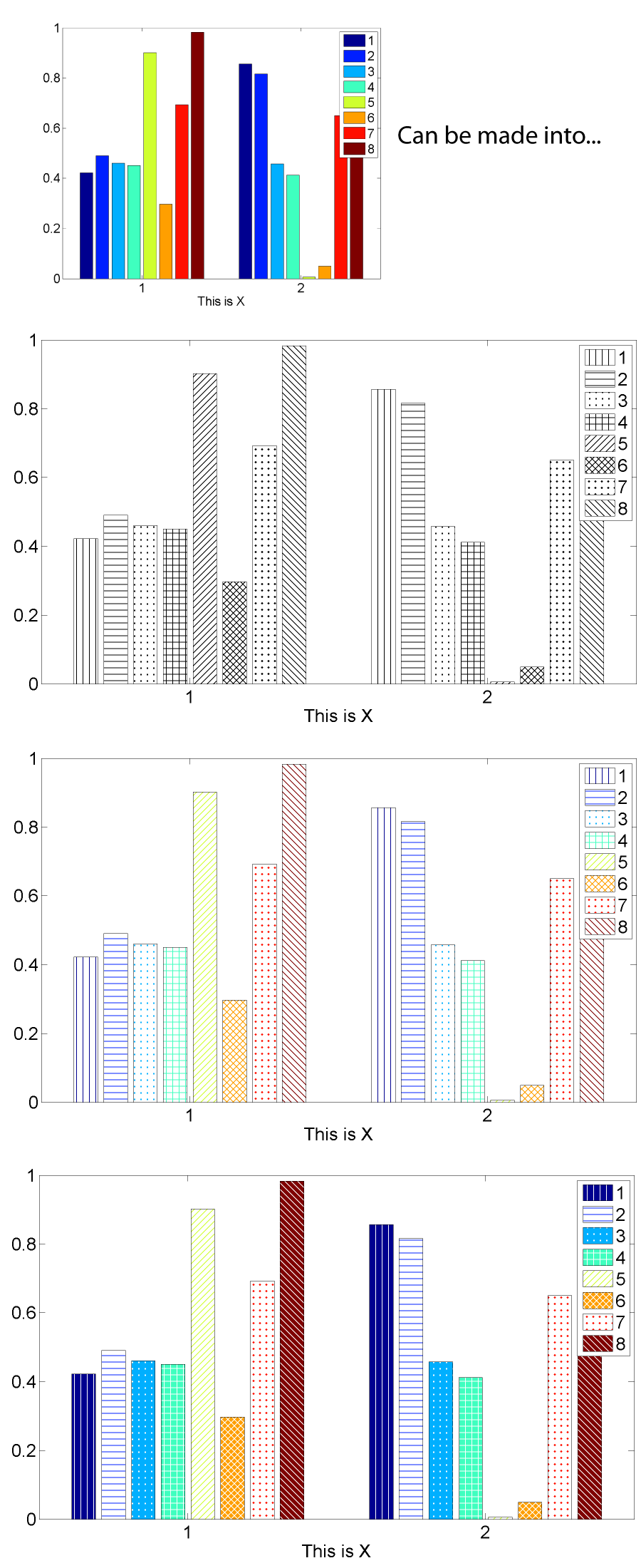
4.1.1 Hachuras em gráficos de barras

Implementar uma função em MATLAB que plote um gráfico de barras com hachuras. O comportamento deve ser semelhante ao comando bar, nativo do MATLAB, mas parâmetros poderão ser acrescentados para controle da trama. Um exemplo de resultado pode ser visto na figura abaixo:

4.1.2 Genius®

Implementar uma versão avançada do jogo Genius® construído na aula 9, adicionando sons, elementos gráficos, etc.

4.1.3 Outros

relógio analógico

dtmf

sudoku

jogo da velha

contar moedas

esteganografia

batalha naval