CEL18702 2016 1 AULA05: mudanças entre as edições
Criou página com '=Análise de Nodal= =Exercícios= =Referências= [1] ----- {| border="1" cellpadding="5" cellspacing="0" ! style="background:#4069e1;" | [[CEL18702_2016_1_AULA04 | <...' |
|||
| (21 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
=Análise de Nodal= | =Análise de Nodal= | ||
Análise de circuitos mais gerais acarreta na solução de um conjunto de | |||
equações. | |||
Análise nodal: | |||
*Tensões são as incógnitas a serem determinadas. | |||
*Deve-se escolher um nó do circuito como referência. | |||
* Associar aos outros nós uma tensão em relação ao nó de referência (tensão de nó). | |||
* Polaridade de um nó é escolhida de tal forma que as tensões dos nós sejam positivas em relação ao nó de referência. | |||
* Nó de referência é geralmente escolhido como o que possui o maior número de ramos conectados. | |||
* Nó de referência possui potencial zero (terra). | |||
* Aplica-se então a lei de Kirchhoff para corrente nos nós. | |||
* As correntes nos elementos são proporcionais às tensões sobre os mesmos. | |||
[[Imagem:fig55_CEL18702.png|center|300px]] | |||
<center> | |||
Figura 1 - Tensões de Nó: <math>V_1</math> e <math>V_2</math>. | |||
</center> | |||
<math>V_{12} = V_1 - V_2\,</math> | |||
<math>V_{13} = V_1 - 0 = V_1\,</math> | |||
<math>V_{23} = V_2 - 0 = V_2\,</math> | |||
[[Imagem:fig56_CEL18702.png|center|600px]] | |||
<center> | |||
Figura 2 - Circuitos com dois Nós. | |||
</center> | |||
;Lei de Kirchhoff de correntes: | |||
'''Nó 1''': <math>i_1+i_2-i_{g1}=0\,</math> ou em termos de tensões: <math>\frac{V_1}{R_1} + \frac{(V_1-V_2)}{R_2}-i_{g1}=0</math> | |||
'''Nó 2''': <math>-i_2+i_3+i_{g2}=0\,</math> ou em termos de tensões: <math>\frac{(V_2-V_1)}{R_2} + \frac{V_2}{R_3}+i_{g2}=0</math> | |||
==Condutância== | |||
Vamos abrir um parênteses para falar sobre condutância. A ideia é que os circuitos fiquem em "termos" de multiplicação e não de divisão. A Figura 3 mostra um exemplo que permite escrever as equações de nós por inspeção direta em função da tensão dos nós. | |||
[[Imagem:fig57_CEL18702.png|center|300px]] | |||
<center> | |||
Figura 3 - Exemplos de circuito resistivo x condutivo. | |||
</center> | |||
<math>V=V_1-V_2\,</math> | |||
<math>i=\frac{V}{R} =\frac{V_1-V_2}{R}\,</math> ou <math>i=\frac{V}{R}=G(V_1-V_2)\,</math> | |||
;Fórmula matemática da condutância: | |||
Para calcular a condutância de um determinado condutor, temos que saber o valor da sua resistência. Assim, e sabendo que a condutância é o inverso da resistência, chegamos à seguinte fórmula: | |||
<math>G=\frac{1}{R}\,</math> | |||
Se tivermos por exemplo, um condutor em que a resistência seja igual a 10Ω, substituímos o R de resistência por 10Ω e obtemos o seguinte cálculo: | |||
;Então: | |||
<math>G=\frac{1}{R}=\frac{1}{10}=0,1 S (siemens) \,</math> | |||
Logo com este cálculo concluímos que um condutor com uma resistência de 10Ω, tem uma condutância de 0,1 siemens. | |||
==Análise com dois nós== | |||
Tomemos um novo exemplo para o qual faremos a mesma análise do exemplo anterior. O | |||
exemplo que se segue é de um circuito com um único par de nós possuindo também fontes | |||
dependentes: | |||
[[Imagem:fig31_CEL18702.png|center|450px]] | |||
<center> | |||
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes. | |||
</center> | |||
Como se pode verificar, a tensão <math>V_1</math> aplicada sobre a condutância de 5 está também aplicada | |||
sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a | |||
seta dirigida para o nó inferior e aplicamos a lei dos nós. | |||
<math>5V_1-0,003+6V_1-20V_1+10V_1+0,013=0\,</math> | |||
<math>1V_1=-0,003-0,013\, \to \, V_1=-0,01V</math> | |||
Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida | |||
ou consumida por cada um dos elementos. | |||
;Na condutância 5 | |||
<math>i_5 = 5V_1=-0,05A\,</math> | |||
<math>P_5 = 5V_1^2=5(-0,01)^2=5.10^{-4}W</math> | |||
;Na condutância 6 | |||
<math>i_6 = 6V_1=-0,06A\,</math> | |||
<math>P_6 = 6V_1^2=5(-0,01)^2=6.10^{-4}W</math> | |||
;Na condutância 10 | |||
<math>i_{10} = 10V_1=-0,1A\,</math> | |||
<math>P_{10} = 10V_1^2=10(-0,01)^2=1.10^{-3}W</math> | |||
;Potência fornecida pela fonte de 3mA: | |||
<math>P_{f3ma} = 0,003V_1 =-0,3.10^{-4}W \, ; \,P_a=0,3.10^{-4}W</math> | |||
;Potência fornecida pela fonte de 13mA: | |||
<math>P_{f13ma} = -0,013V_1 =-1,3.10^{-4}W\,</math> | |||
;Potência fornecida pela fonte dependente: | |||
<math>P_{f20Vx} = 20V_1.V_1 = 20V_1^2=20(-0,01)^2=20.10^{-4}W\,</math> | |||
;Por último, fazemos o balanço das potências: | |||
<math> | |||
\sum_{\,}^{\,} P_f = 1,3.10^{-4}+20.10^{-4}=21,3.10^{-4}W | |||
</math> | |||
<math> | |||
\sum_{\,}^{\,} P_a = 5.10^{-4}+6.10^{-4}+0,3.10^{-4}=21,3.10^{-4}W | |||
</math> | |||
=Exercício de fixação= | |||
[1] '''Fonte independente''' de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito. | |||
[[Imagem:fig33_CEL18702.png|center|450px]] | |||
{{collapse top|Solução}} | |||
;malha 1 | |||
<math> | |||
-6+2(i_1-i_2)+1(i_1-i_3)=0 \quad \to \quad -6+2i_1-2i_2+1_1-6=0 \quad \to \quad 3i_1-2i_2=12 | |||
</math> | |||
;malha 2 | |||
<math> | |||
4i_2+3(i_2-i_3)+2(i_2-i_1)=0 \quad \to \quad 4i_2+3i_2-18+2i_2-2i_1=0 \quad \to \quad -2i_1+9_i2=18 | |||
</math> | |||
;Resolvendo o sistema (Cramer): | |||
<math> | |||
\Delta=\begin{vmatrix} 3 & -2 \\ -2 & 9 \end{vmatrix}\,.\,\begin{vmatrix} 12 \\ 18 \end{vmatrix} | |||
</math> | |||
<math> | |||
\Delta=\begin{vmatrix} 3 & -2 \\ -2 & 9 \end{vmatrix}\,=27-(4)\qquad \Delta=23 | |||
</math> | |||
<math> | |||
\Delta i_1=\begin{vmatrix} 12 & -2 \\ 18 & 9 \end{vmatrix}\,=108-(-36)\qquad \Delta i_1=144 | |||
</math> | |||
<math> | |||
\Delta i_2=\begin{vmatrix} 3 & 12 \\ -2 & 18 \end{vmatrix}\,=54-(-24)\qquad \Delta i_2=78 | |||
</math> | |||
<math>i_1=\frac{\Delta i_1}{\Delta}=\frac{144}{23} \qquad i_1=6,26A\,</math> | |||
<math>i_2=\frac{\Delta i_2}{\Delta}=\frac{78}{23} \qquad i_2=3,39A\,</math> | |||
{{collapse bottom}} | |||
[2] '''Fonte dependente''' de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito. | |||
[[Imagem:fig34_CEL18702.png|center|450px]] | |||
{{collapse top|Solução}} | |||
;malha 1 | |||
<math> | |||
-6+2(i_1-i_2)+1(i_1-i_3)=0 \quad \to \quad -6+2i_1-2i_2+i_1-i_3=0 \quad \to \quad 3i_1-2i_2-i_3=6 | |||
</math> | |||
;malha 2 | |||
<math> | |||
4i_2+3(i_2-i_3)+2(i_2-i_1)=0 \quad \to \quad 4i_2+3i_2-3i_3+2i_2-2i_1=0 \quad \to \quad -2i_1+9i_2-3i_3=0 | |||
</math> | |||
;malha 3 | |||
<math>i_3=\frac{i_a}{3}</math> | |||
;Se: | |||
<math>i_1=i_a \quad logo \quad i_3=\frac{i_1}{3}</math> | |||
;Resolvendo o sistema: | |||
<math> | |||
3i_1-2i_2-i_3=6 \quad \to \quad 3i_1-2i_2-\frac{i_1}{3}=6 \quad \to \quad \frac{8i_1}{3}-2i_2=6 | |||
</math> | |||
<math> | |||
-2i_1+9i_2-3i_3=0 \quad \to \quad -2i_1+9i_2-3\frac{i_1}{3}=0 \quad \to \quad -3i_1+9i_2=0 | |||
</math> | |||
<math> | |||
\Delta=\begin{vmatrix} \frac{8}{3} & -2 \\ -3 & 9 \end{vmatrix}\,.\,\begin{vmatrix} 6 \\ 0 \end{vmatrix} | |||
</math> | |||
<math> | |||
\Delta=\begin{vmatrix} \frac{8}{3} & -2 \\ -3 & 9 \end{vmatrix}\,=24-(6) \qquad \Delta=18 | |||
</math> | |||
<math> | |||
\Delta i_1=\begin{vmatrix} 6 & -2 \\ 0 & 9 \end{vmatrix}\,=54-(0)\qquad \Delta i_1=54 | |||
</math> | |||
<math> | |||
\Delta i_2=\begin{vmatrix} \frac{8}{3} & 6 \\ -3 & 0 \end{vmatrix}\,=0-(-18)\qquad \Delta i_2=18 | |||
</math> | |||
<math>i_1=\frac{\Delta i_1}{\Delta}=\frac{54}{18} \qquad i_1=3A\,</math> | |||
<math>i_2=\frac{\Delta i_2}{\Delta}=\frac{18}{18} \qquad i_2=1A\,</math> | |||
<math>i_3=\frac{i_1}{3}=\frac{3}{3} \qquad i_3=1 A\,</math> | |||
{{collapse bottom}} | |||
=Exercício= | |||
Encontra as correntes do circuito abaixo e calcule a potência de todos os elementos. | |||
[[Imagem:fig35_CEL18702.png|center|450px]] | |||
=Referências= | =Referências= | ||
[1] | [1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf | ||
Edição atual tal como às 21h01min de 26 de abril de 2016
1 Análise de Nodal
Análise de circuitos mais gerais acarreta na solução de um conjunto de equações. Análise nodal:
- Tensões são as incógnitas a serem determinadas.
- Deve-se escolher um nó do circuito como referência.
- Associar aos outros nós uma tensão em relação ao nó de referência (tensão de nó).
- Polaridade de um nó é escolhida de tal forma que as tensões dos nós sejam positivas em relação ao nó de referência.
- Nó de referência é geralmente escolhido como o que possui o maior número de ramos conectados.
- Nó de referência possui potencial zero (terra).
- Aplica-se então a lei de Kirchhoff para corrente nos nós.
- As correntes nos elementos são proporcionais às tensões sobre os mesmos.
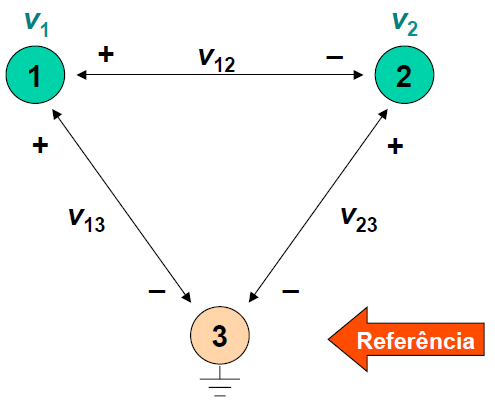
Figura 1 - Tensões de Nó: e .
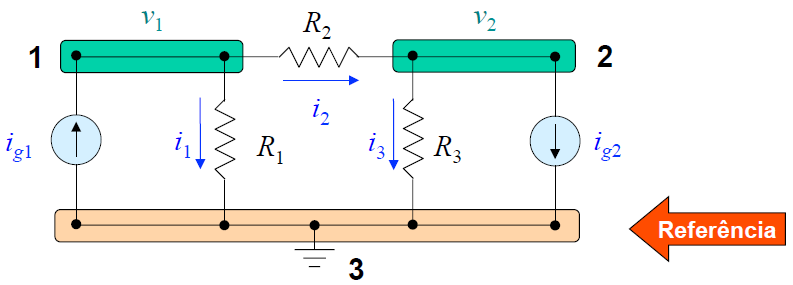
Figura 2 - Circuitos com dois Nós.
- Lei de Kirchhoff de correntes
Nó 1: ou em termos de tensões:
Nó 2: ou em termos de tensões:
1.1 Condutância
Vamos abrir um parênteses para falar sobre condutância. A ideia é que os circuitos fiquem em "termos" de multiplicação e não de divisão. A Figura 3 mostra um exemplo que permite escrever as equações de nós por inspeção direta em função da tensão dos nós.
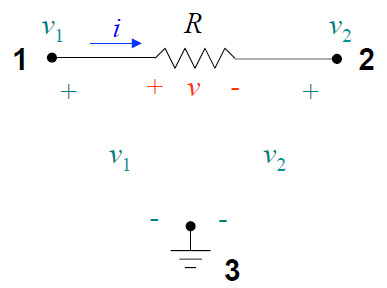
Figura 3 - Exemplos de circuito resistivo x condutivo.
ou
- Fórmula matemática da condutância
Para calcular a condutância de um determinado condutor, temos que saber o valor da sua resistência. Assim, e sabendo que a condutância é o inverso da resistência, chegamos à seguinte fórmula:
Se tivermos por exemplo, um condutor em que a resistência seja igual a 10Ω, substituímos o R de resistência por 10Ω e obtemos o seguinte cálculo:
- Então
Logo com este cálculo concluímos que um condutor com uma resistência de 10Ω, tem uma condutância de 0,1 siemens.
1.2 Análise com dois nós
Tomemos um novo exemplo para o qual faremos a mesma análise do exemplo anterior. O exemplo que se segue é de um circuito com um único par de nós possuindo também fontes dependentes:
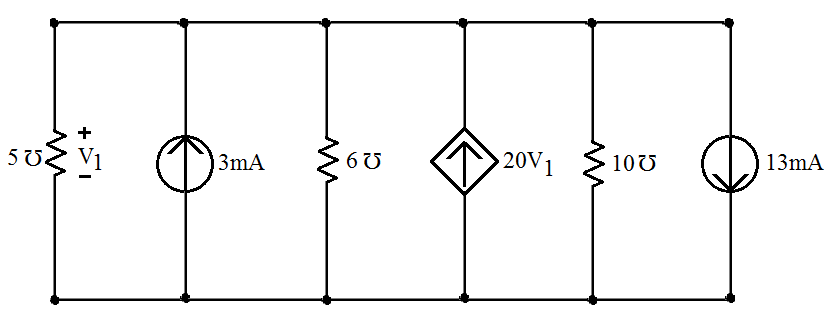
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes.
Como se pode verificar, a tensão aplicada sobre a condutância de 5 está também aplicada
sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a
seta dirigida para o nó inferior e aplicamos a lei dos nós.
Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida ou consumida por cada um dos elementos.
- Na condutância 5
- Na condutância 6
- Na condutância 10
- Potência fornecida pela fonte de 3mA
- Potência fornecida pela fonte de 13mA
- Potência fornecida pela fonte dependente
- Por último, fazemos o balanço das potências
2 Exercício de fixação
[1] Fonte independente de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito.
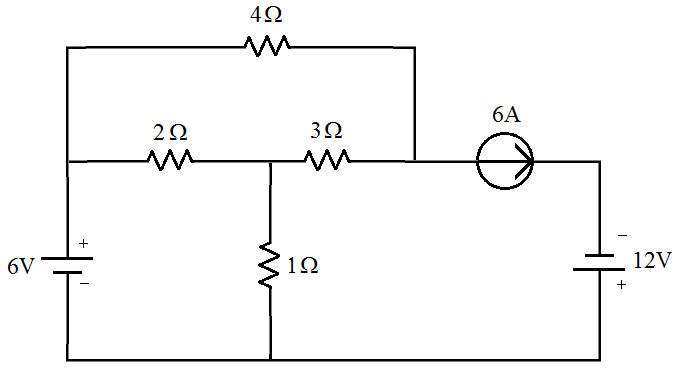
| Solução |
|---|
|
[2] Fonte dependente de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito.
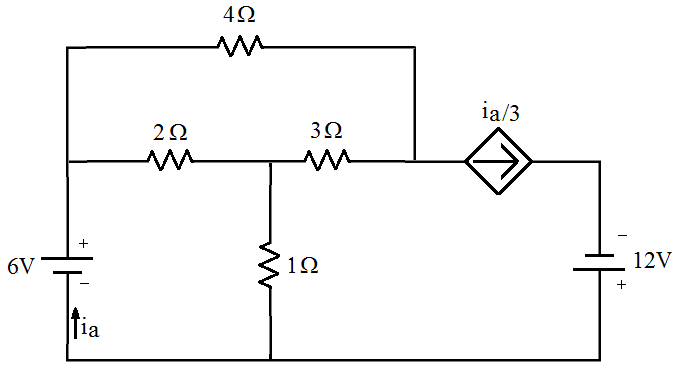
| Solução |
|---|
|
3 Exercício
Encontra as correntes do circuito abaixo e calcule a potência de todos os elementos.
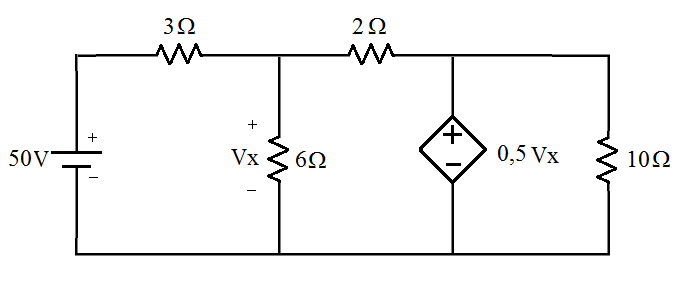
4 Referências
[1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf
| << | <> | >> |
|---|