Monitoria de Circuitos e Eletrônica: mudanças entre as edições
Criou página com 'Associação de Resistências : Formula Geral Zeq = <math>\int_{-N}^{N} e^x\, dx\frac{R1}{4} </math> Arquivo:DivisorTensao.png' |
|||
| (19 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
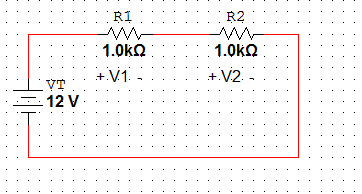
==Divisor de tensão com resistência== | |||
[[Arquivo:R.jpg]] | |||
[[Arquivo: | <math>V_{2} = \frac{R_2}{R_1+R_2} \cdot V_{T} | ||
</math> | |||
<math>V_{1} = \frac{R_1}{R_1+R_2} \cdot V_{T} | |||
</math> | |||
== Divisor de tensão com impedância == | |||
Um divisor de tensão é geralmente imaginado como composto por dois resistores, porém [[capacitor]]es, [[indutor]]es, ou qualquer [[impedância]] combinada pode ser utilizada. Para impedâncias gerais ''Z''<sub>1</sub> e ''Z''<sub>2</sub>, a tensão é dada por | |||
:<math> | |||
V_{2} = \frac{Z_2}{Z_1+Z_2} \cdot V_{T} | |||
</math> | |||
:<math> | |||
V_{1} = \frac{Z_1}{Z_1+Z_2} \cdot V_{T} | |||
</math> | |||
A impedância do resistor é igual à sua [[resistência]]: | |||
:<math> | |||
Z_R = R | |||
</math> | |||
A [[Reatância capacitiva|impedância do capacitor e indutor]] varia de acordo com a [[frequência]] de V_{entrada}. Seu valor é dado por: | |||
:<math> | |||
Z_C = {1 \over j \omega C} | |||
</math> | |||
:<math> | |||
Z_L = { j \omega L} | |||
</math> | |||
onde: | |||
* ''j'' é a [[unidade imaginária]] | |||
* ''ω'' é a [[frequência angular]] em [[radiano]]s por [[segundo]]s. Este divisor de tensão terá a | |||
== Divisor de corrente com resistores == | |||
Neste circuito, dois [[resistor]]es são conectados em [[ligação paralela|paralelo]]: | |||
A corrente nos resistores é inversamente proporcional a resistencia daquele no qual está passando, ou seja: | |||
<math> | |||
I_{1} = \frac{R_2}{R_1+R_2} \cdot I_T | |||
</math> | |||
<math> | |||
I_{2} = \frac{R_1}{R_1+R_2} \cdot I_T | |||
</math> | |||
== Divisor de corrente com impedância == | |||
<math> | |||
I_{1} = \frac{Z_2}{Z_1+Z_2} \cdot I_T | |||
</math> | |||
<math> | |||
I_{2} = \frac{Z_1}{Z_1+Z_2} \cdot I_T | |||
</math> | |||
A forma de onda de corrente e tensão em CA pode ser descrita matematicamente através da fórmula: | |||
:<math> | |||
v(t)=V \cdot \sin(2 \pi f t + \phi_{v})\, | |||
= V \angle \phi_{v} </math> | |||
:<math> | |||
i(t)=I \cdot \sin(2 \pi f t + \phi_{i})\, | |||
= I \angle \phi_{i} </math> | |||
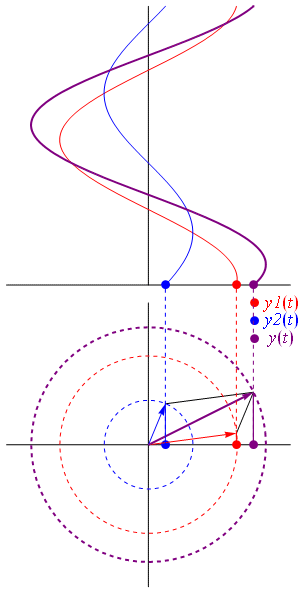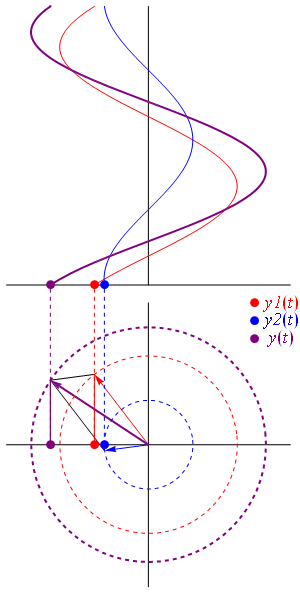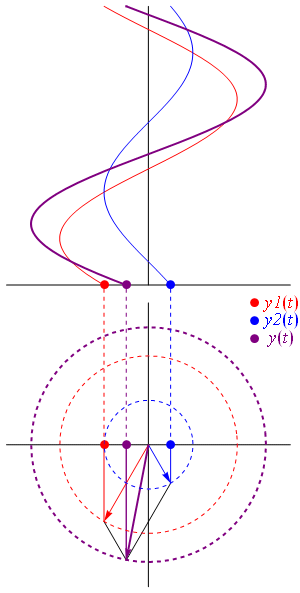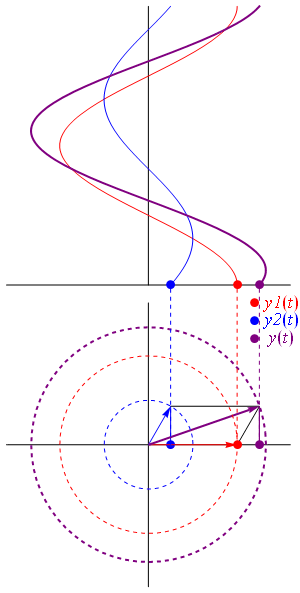
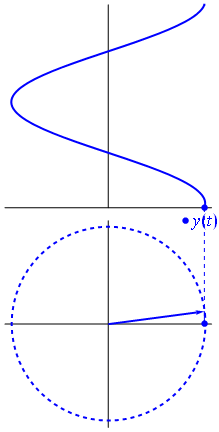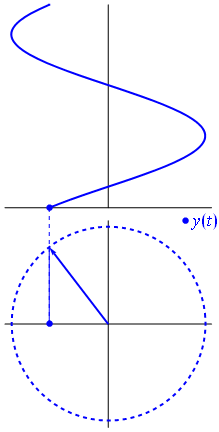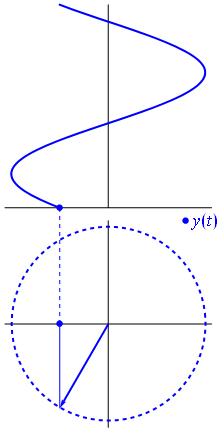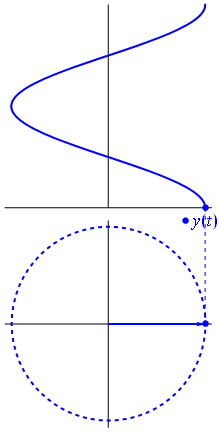
Uma onda [[co-seno]] também é considerada [[sinusoidal]], visto que ela possui o mesmo formato porém está defasada com relação à onda seno no eixo horizontal: <math>\cos\left(\theta -\frac{\pi}{2}\right) = \sin{\theta}</math> | |||
==Identidades trigonométricas== | |||
Para ângulos em graus: | |||
:<math>\sin \left(\omega t \pm 180 \right) = -\sin{\omega t}</math> | |||
:<math>\cos \left(\omega t \pm 180 \right) = -\cos{\omega t}</math> | |||
:<math>\sin \left(\omega t \pm 90 \right) = \pm \cos{\omega t}</math> | |||
:<math>\cos \left(\omega t \pm 90 \right) = \mp \sin{\omega t}</math> | |||
Para ângulos em radianos: | |||
:<math>\sin \left(\omega t \pm \pi \right) = -\sin{\omega t}</math> | |||
:<math>\cos \left(\omega t \pm \pi \right) = -\cos{\omega t}</math> | |||
:<math>\sin \left(\omega t \pm \pi/2 \right) = \pm \cos{\omega t}</math> | |||
:<math>\cos \left(\omega t \pm \pi/2 \right) = \mp \sin{\omega t}</math> | |||
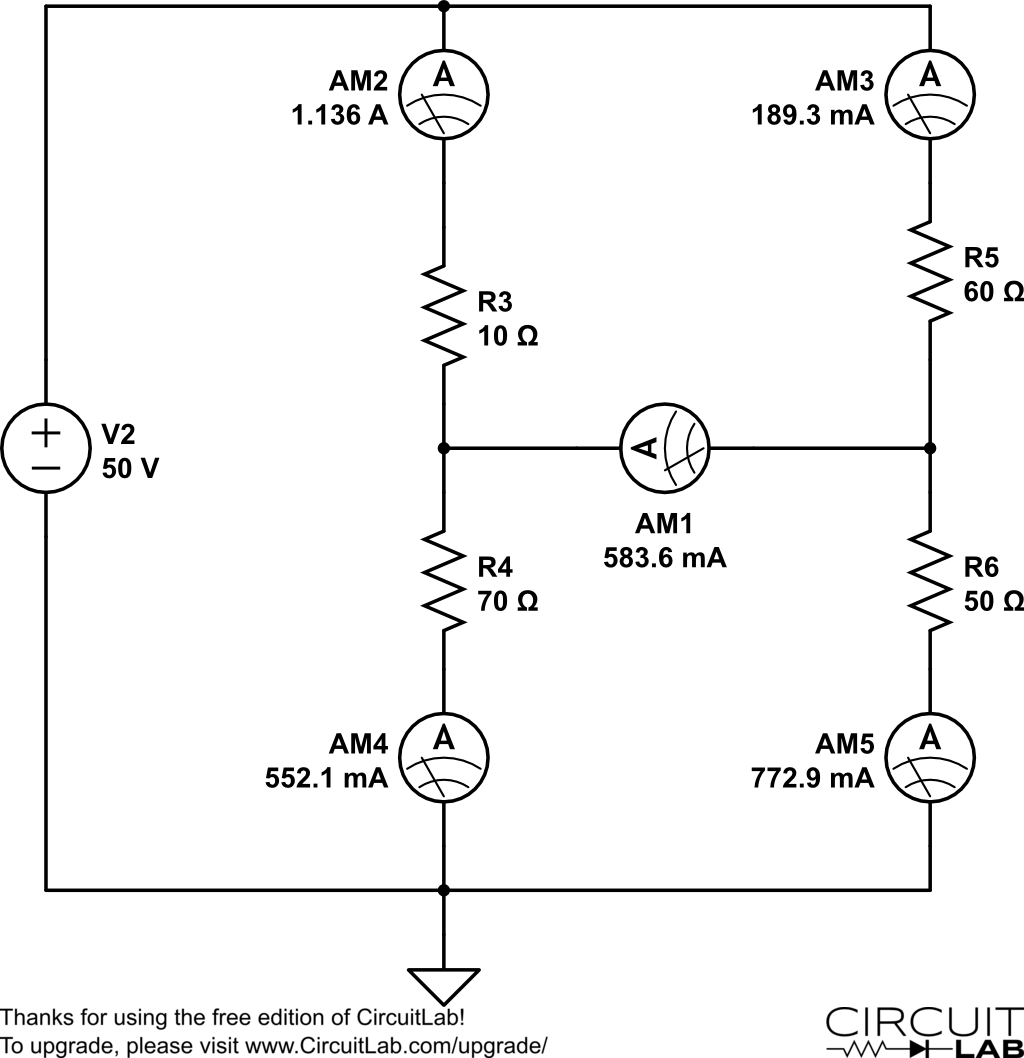
== Analise Nodal == | |||
[[Arquivo:a.jpg|thumb|center|400px]] | |||
== Defasagem de ondas == | |||
[[Arquivo:F.jpg|thumb|left|300px]] | |||
[[Arquivo:S.jpg|thumb|center|500px|]] | |||
[[Categoria:Monitoria]] | |||
Edição atual tal como às 09h56min de 30 de junho de 2021
1 Divisor de tensão com resistência
2 Divisor de tensão com impedância
Um divisor de tensão é geralmente imaginado como composto por dois resistores, porém capacitores, indutores, ou qualquer impedância combinada pode ser utilizada. Para impedâncias gerais Z1 e Z2, a tensão é dada por
A impedância do resistor é igual à sua resistência:
A impedância do capacitor e indutor varia de acordo com a frequência de V_{entrada}. Seu valor é dado por:
onde:
- j é a unidade imaginária
- ω é a frequência angular em radianos por segundos. Este divisor de tensão terá a
3 Divisor de corrente com resistores
Neste circuito, dois resistores são conectados em paralelo:
A corrente nos resistores é inversamente proporcional a resistencia daquele no qual está passando, ou seja:
4 Divisor de corrente com impedância
A forma de onda de corrente e tensão em CA pode ser descrita matematicamente através da fórmula:
Uma onda co-seno também é considerada sinusoidal, visto que ela possui o mesmo formato porém está defasada com relação à onda seno no eixo horizontal:
5 Identidades trigonométricas
Para ângulos em graus:
Para ângulos em radianos:
6 Analise Nodal
7 Defasagem de ondas