Transformadas de Fourier: mudanças entre as edições

Edição atual tal como às 15h58min de 19 de novembro de 2020

1 Transformada de Fourier no tempo contínuo (TFTC)

O sinal $x (t)$ é contínuo no tempo, e o sinal $X (j Ω)$ é contínuo na frequência.

A equação de análise: É uma transformação de um domínio de uma variável real $x (t)$ de tempo continuo em uma variável complexa $X (j Ω)$ de frequência contínua.; $D T \to D F$ .

x : ℝ \to ℂ

.

X (j Ω) \equiv ℱ {x (t)} \overset{d e f}{=} \int_{- \infty}^{\infty} x (t) e^{- j Ω t} d t

A equação de síntese: É uma transformação de um domínio de uma variável complexa $X (j Ω)$ de frequência contínua em uma variável real $x (t)$ de tempo continuo.; $D F \to D T$ .

X : ℂ \to ℝ

.

x (t) \equiv ℱ^{- 1} {X (j Ω)} \overset{d e f}{=} \frac{1}{2 π} \int_{- \infty}^{\infty} X (j Ω) e^{j Ω t} d Ω

A transformada de Fourier

X (j Ω)

, por simplificação é muitas vezes representada apenas por

X (Ω)

ou

X (ω)

, mas é importante lembrar que tratasse de uma frequência complexa, representada pelo eixo imaginário do plano s.

Figura 1 - Sinal

x (t)

e sua transformada de Fourier

X (Ω)

Fonte: Elaborado pelo autor.

Para relembrar os conceitos vistos em Sinais e Sistemas, recomendo assitir os vídeos sobre Transformada de Fourier do prof. Luis Antonio Aguirre da UFMG

Introdução a Transformada de Fourier	Existência da Transformada Fourier	Transformada de Fourier: Propriedades 1	Transformada de Fourier: Propriedades 2	Transformada de Fourier para Sinais Periodicos
Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade

2 Transformada Z

A transformada Z de um sinal de tempo discreto $x (n)$ é a função $X (z)$ definida como

X (z) = Z {x (n)} = \sum_{n = - \infty}^{\infty} x (n) z^{- n}

onde

n

é um inteiro;

z = A e^{j ϕ}

é um número complexo, com

A

sendo sua magnitude, e

ϕ

sua frequência angular (em radianos por amostra).

A transformada Z inversa é

x (n) = Z^{- 1} {X (z)} = \frac{1}{2 π j} \oint_{C} X (z) z^{n - 1} d z

onde $C$ é o caminho antihorário envolvendo a origem, dentro da região de convergencia (ROC) de $X (z)$ .

3 Transformada de Fourier de tempo discreto (TFTD)

O sinal $x (n)$ é discreto no tempo, e o sinal $X (Ω)$ é contínuo e periódico em $2 π$ .

A equação de análise: É uma transformação de um domínio de uma variável real $x (n)$ de tempo discreto em uma variável complexa $X (e^{j ω})$ frequência contínua periódica.; $D T \to D F$ .

x : ℝ \to ℂ

.

X (e^{j ω}) \equiv ℱ {x (n)} \overset{d e f}{=} \sum_{n = - \infty}^{\infty} x (n) e^{- j ω n}

A equação de síntese: É uma transformação de um domínio de uma variável complexa $X (e^{j ω})$ de frequência contínua periódica em uma variável real $x (n)$ continua.; $D F \to D T$ .

X : ℂ \to ℝ

.

x (n) \equiv ℱ^{- 1} {X (e^{j ω})} \overset{d e f}{=} \frac{1}{2 π} \int_{- \infty}^{\infty} X (e^{j ω}) e^{j ω n} d ω

Como a transformada de Fourier $X (e^{j ω})$ é periódica com período $2 π$ , pois $X (e^{j ω}) = X (e^{j (ω + 2 π k)})$ , para $k \in ℤ$ , ela pode ser calculada em qualquer faixa de $2 π$ , por exemplo $ω \in [- π, π)$ .

x (n) \equiv ℱ^{- 1} {X (e^{j ω})} \overset{d e f}{=} \frac{1}{2 π} \int_{- π}^{π} X (e^{j ω}) e^{j ω n} d ω

Figura 2 - Sinal discreto

x (n)

e sua TFDT

X (e^{j ω})

Fonte: Elaborado pelo autor.

4 Série de Fourier de tempo contínuo (SF)

O sinal $x (t)$ é contínuo e periódico no tempo (com período $T$ ) , e o sinal $X (k)$ é discreto na frequência.

A equação de análise: É uma transformação de um domínio de uma variável real $x (t)$ de tempo continuo em uma variável complexa $X (k)$ de frequência discreta.; $D T \to D F$ .

x : ℝ \to ℂ

.

X (k) = \frac{1}{T} \int_{0}^{T} x (t) e^{- j (2 π / T) k t)} d t

A equação de síntese: É uma transformação de um domínio de uma variável complexa $X (k)$ de frequência contínua em uma variável real $x (t)$ de tempo continuo.; $D F \to D T$ .

X : ℂ \to ℝ

.

x (t) = \sum_{k = - \infty}^{\infty} X (k) e^{j (2 π / T) k t)}

A série de Fourier

X (k)

, indicada acima é a série exponencial onde as funções de base são exponenciais complexas

e^{- j ω t}

, onde

ω = (2 π / T) k

. Também existem as séries de Fourier usando funções de base senoidais e cossenoidais, as quais podem ser derivadas da série exponencial.

Figura 3 - Sinal

x (t)

periódico e sua série de Fourier

X (Ω)

Arquivo:SerieFourierPlot.png Fonte: Elaborado pelo autor.

5 Transformada de Discreta de Fourier (TDF)

Discrete Fourier Transform (DFT).

5.1 Obtenção da TDF a partir da amostragem da TFTD

Sinais discretos no tempo podem ser representados pela sua TFTD, que é uma função continua periódica em $2 π$ de $ω$ :

X (e^{j ω}) = \sum_{n = - \infty}^{\infty} x (n) e^{- j ω n}

Para que a mesma possa ser utilizada no processamento de sinais digitais é necessário que a variável frequência seja também discreta. Se amostrarmos uniformemente a frequência $ω$ em N amostras entre 0 e $2 π$ é possível obter a TDF (ou DFT - Discrete Fourier Transform). Assim se tomarmos N frequências $ω_{k} = (2 π / N) k$ com $k \in ℤ$ , and $0 \leq k \leq N - 1$ , obtemos o espectro amostrado uniformemente:

X^{'} (e^{j ω}) = X (e^{j ω}) \sum_{k = - \infty}^{\infty} δ (ω - \frac{2 π}{N} k)

.

X^{'} (e^{j ω}) = \sum_{n = - \infty}^{\infty} x (n) e^{- j \frac{2 π}{N} k n}

O sinal equivalente no tempo pode ser obtido aplicando a transformada inversa e a convolução:

x^{'} (n) = ℱ^{- 1} {X^{'} (e^{j ω})} = x (n) * (\frac{N}{2 π} \sum_{p = - \infty}^{\infty} δ (n - N p)) = \frac{N}{2 π} \sum_{p = - \infty}^{\infty} x (n - N p)

.

O que mostra que o sinal Esse sinal $x^{'} (n)$ são repetições periódicas (com período N) do sinal discreto $x (n)$ original.

Note que N o período de repetição do sinal $x^{'} (n)$ é o mesmo período de repetição das N amostras da TFTD $X (e^{j ω})$ original.
Se o comprimento L o sinal do $x (n)$ for maior que N o período de repetição do sinal $x^{'} (n)$ , haverá sobreposição das amostras no tempo (time aliasing), e não será possível recuperar o sinal original.
Por outro lado, se $L \leq N$ então $x^{'} (n)$ é a repetição periódica exata de $x (n)$ .

x (n) = \frac{2 π}{N} x^{'} (n)

, para

0 \leq n \leq N - 1

ou

x (n) = \frac{2 π}{N} x^{'} (n) [u (n) - u (n - N)

.

Portanto, é possível recuperar as amostras do sinal digital no tempo $x (n)$ a partir das suas amostras digitais na frequência, desde que o período de repetição das N amostras de frequência seja maior ou igual ao comprimento L do sinal no tempo.

5.2 TDF e TDFI

O sinal $x (n)$ é discreto no tempo pode ser representado pelo o sinal $X (e^{j (2 π / N) k})$ ou $X (k)$ discreto e periódico em $2 π$ .

Para obter a equação de análise (DFT) pode ser feito o cálculo das amostras do espectro de frequências em $ω_{k} = (2 π / N) k$ em:

X (e^{j ω}) = \sum_{n = - \infty}^{\infty} x (n) e^{- j ω n}

X (e^{j (2 π / N) k}) = \sum_{n = - \infty}^{\infty} x (n) e^{- j (2 π / N) k n}

Conforme mostrado, o espectro é periódico em N, e portanto é suficiente calcular apenas os valores para $0 \leq k \leq N - 1$ . Assim obtém-se

A equação de análise (TDF): É uma transformação de um domínio de uma variável real $x (n)$ de tempo discreto em uma variável complexa $X (e^{j (2 π / N) k})$ frequência discreta periódica.; $D T \to D F$ .

x : ℝ \to ℂ

.

X (e^{j (2 π / N) k}) \equiv ℱ {x (n)} \overset{d e f}{=} \sum_{n = 0}^{N - 1} x (n) e^{- j (2 π / N) k n}

, para

0 \leq k \leq N - 1

A equação de síntese (TDFI): É uma transformação de um domínio de uma variável complexa $X (e^{j (2 π / N) k})$ de frequência discreta periódica em uma variável real $x (n)$ discreta.; $D F \to D T$ .

X : ℂ \to ℝ

.

x (n) \equiv ℱ^{- 1} {X (e^{j (2 π / N) k})} \overset{d e f}{=} \frac{1}{N} \sum_{k = 0}^{N - 1} X (e^{j (2 π / N) k}) e^{j (2 π / N) k n}

, para

0 \leq n \leq N - 1

Ao usar a equação de análise, se o comprimento L de $x (n)$ for menor que o período de repetição N, é necessário que $x (n)$ seja preenchido com amostras nulas até atingir o comprimento N (zero-padding).

5.3 Equação simplificada da TDF e TDFI

Para simplificar a notação pode-se utilizar para representar as frequência discreta:

X (k) = X (e^{j (2 π / N) k})

,

definir a frequência fundamental $ω_{N}$ como:

ω_{N} = e^{- j 2 π / N}

então

e^{- j (2 π / N) k} = ω_{N}^{k}

Essa frequência corresponde a uma posição no circulo unitário do plano complexo $z$ .

Alguns valores de $ω_{N}$ que ajudam a lembrar as simplificações:

ω_{1} = e^{- j 2 π} = + 1

ω_{- 1} = e^{j 2 π} = + 1

ω_{2} = e^{- j π} = - 1

ω_{- 2} = e^{j π} = - 1

ω_{4} = e^{- j π / 2} = - j

ω_{- 4} = e^{j π / 2} = + j

Também é importante lembrar que se $N$ é múltiplo de $k$ então:

ω_{N}^{k} = e^{- j (2 π / N) k} = e^{- j 2 π / (N / k)} = ω_{N / k}

Dessa forma as equações da TDF e TDFI passam a ser escritas de forma simplificada como:

Equação de análise: $X (k) = \sum_{n = 0}^{N - 1} x (n) ω_{N}^{k n}$ , para $0 \leq k \leq N - 1$

Equação de síntese: $x (n) = \frac{1}{N} \sum_{k = 0}^{N - 1} X (k) ω_{N}^{- k n}$ , para $0 \leq n \leq N - 1$

Dessas equações é possível perceber que o cálculo da TDF e da TDFI requerem a $N^{2}$ multiplicações e $N (N - 1)$ somas, sendo portanto um algoritmo de $O (N^{2})$ .

5.4 Notação matricial de TDF e TDFI

Em notação matricial cada $X (k)$ na TDF e $x (k)$ na TDFI podem ser calculado como:

X (k) = [\begin{matrix} ω_{N}^{0} & ω_{N}^{k} & ω_{N}^{2 k} & . . . & ω_{N}^{(N - 1) k} \end{matrix}] \times [\begin{matrix} x (0) \\ x (1) \\ x (2) \\ ⋮ \\ x (N - 1) \end{matrix}]

x (k) = \frac{1}{N} [\begin{matrix} ω_{N}^{0} & ω_{N}^{- k} & ω_{N}^{- 2 k} & . . . & ω_{N}^{- (N - 1) k} \end{matrix}] \times [\begin{matrix} X (0) \\ X (1) \\ X (2) \\ ⋮ \\ X (N - 1) \end{matrix}]

Porém como $ω_{N}^{0} = 1$ as equações TDF e TDFI podem ser escritas em notação matricial:

Equação de análise: $[\begin{matrix} X (0) \\ X (1) \\ X (2) \\ ⋮ \\ X (N - 1) \end{matrix}] = [\begin{matrix} 1 & 1 & 1 & . . . & 1 \\ 1 & ω_{N}^{1} & ω_{N}^{2} & . . . & ω_{N}^{(N - 1)} \\ 1 & ω_{N}^{2} & ω_{N}^{4} & . . . & ω_{N}^{2 (N - 1)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & ω_{N}^{(N - 1)} & ω_{N}^{2 (N - 1)} & . . . & ω_{N}^{(N - 1)^{2}} \end{matrix}] \times [\begin{matrix} x (0) \\ x (1) \\ x (2) \\ ⋮ \\ x (N - 1) \end{matrix}]$

Equação de síntese: $[\begin{matrix} x (0) \\ x (1) \\ x (2) \\ ⋮ \\ x (N - 1) \end{matrix}] = \frac{1}{N} [\begin{matrix} 1 & 1 & 1 & . . . & 1 \\ 1 & ω_{N}^{- 1} & ω_{N}^{- 2} & . . . & ω_{N}^{- (N - 1)} \\ 1 & ω_{N}^{- 2} & ω_{N}^{- 4} & . . . & ω_{N}^{- 2 (N - 1)} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & ω_{N}^{- (N - 1)} & ω_{N}^{- 2 (N - 1)} & . . . & ω_{N}^{- (N - 1)^{2}} \end{matrix}] \times [\begin{matrix} X (0) \\ X (1) \\ X (2) \\ ⋮ \\ X (N - 1) \end{matrix}]$

5.5 Transformada Rápida de Fourier (FFT)

O cálculo da TDF e TDFI para uma sequência de dados de comprimento $N$ necessita de $N^{2}$ multiplicações complexas, limitando o seu uso em aplicações práticas. Em 1965, Cooley e Tukey propuseram um algoritmo rápido (FFT) para calcular a TDF com um número de multiplicações complexas na ordem de $O (N \times l o g_{2} N)$ . Esse mudança faz com que uma sequência de comprimento 1024, calculado com a TDF demanda 1024x1024 multiplicações, enquanto que com a FFT apenas 1024x10. Isso representa neste caso uma redução de complexidade de 100 vezes.

Atualmente existem diversos algoritmos de FFT, que obtêm exatamente o mesmo valor que o uso da TDF, mas eles podem ser classificados de forma geral em decimação no tempo, ou decimação na frequência, dependendo de qual vetor será decimado e reordenado, se o sinal no tempo $x (n)$ ou as frequencia $X (k)$ .

Ver este e-book The DFT, FFT, and Practical Spectral Analysis em OpenStax CNX, e também a wikipedia que tem esse artigo muito bem escrito sobre o assunto.

Para relembrar os conceitos vistos acima, recomendo assistir os vídeos sobre DFT e FFT do prof. Steve Brunton da University of Washington

The Discrete Fourier Transform (DFT)	Computing the DFT Matrix	The Fast Fourier Transform (FFT)	The Fast Fourier Transform Algorithm	What is a Fast Fourier Transform (FFT)?
Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade	Carregar vídeo YouTube YouTube pode coligir dados pessoais. Politica de privacidade

6 Soma dos termos de uma Progressão Geométrica

A soma aritmética dos termos de uma P.G. a partir do primeiro termo, é definida por:

S_{n} = = a_{1} + a_{1} q + a_{1} q^{2} + \dots + a_{1} q^{n - 1} = \sum_{i = 1}^{n} a_{1} q^{i - 1}

Caso $q \neq 1$ , a soma pode ser descrita por:

S_{n} = \frac{a_{1} (1 - q^{n})}{1 - q}

Transformadas de Fourier: mudanças entre as edições

Edição atual tal como às 15h58min de 19 de novembro de 2020

Índice

1 Transformada de Fourier no tempo contínuo (TFTC)

2 Transformada Z

3 Transformada de Fourier de tempo discreto (TFTD)

4 Série de Fourier de tempo contínuo (SF)

5 Transformada de Discreta de Fourier (TDF)

5.1 Obtenção da TDF a partir da amostragem da TFTD

5.2 TDF e TDFI

5.3 Equação simplificada da TDF e TDFI

5.4 Notação matricial de TDF e TDFI

5.5 Transformada Rápida de Fourier (FFT)

6 Soma dos termos de uma Progressão Geométrica

Menu de navegação

@@ Linha 22: / Linha 22: @@
 {{fig|1|Sinal <math> \mathrm{x(t)} </math> e sua transformada de Fourier <math> \mathrm{X(\Omega)} </math>| FourierPlot.png| 800 px |}}
+*Para relembrar os conceitos vistos em Sinais e Sistemas, recomendo assitir os vídeos sobre Transformada de Fourier do prof. Luis Antonio Aguirre da UFMG
+{| class="wikitable"
+|-
+! Introdução a Transformada de Fourier
+! Existência da Transformada Fourier
+! Transformada de Fourier: Propriedades 1
+! Transformada de Fourier: Propriedades 2
+! Transformada de Fourier para Sinais Periodicos
+|-
+|{{#ev:youtube|vDSN2sLF3gM|300}}
+|{{#ev:youtube|9i3c1YkrDkI|300}}
+|{{#ev:youtube|EvnxPJKNOO4|300}}
+|{{#ev:youtube|AmeZHZRZTUw|300}}
+|{{#ev:youtube|2qsreRJgdaI|300}}
+|}
 ==Transformada Z ==
@@ Linha 37: / Linha 53: @@
 onde <math> C \ </math> é o caminho antihorário envolvendo a origem, dentro da região de convergencia (ROC) de <math>X(z)\, </math>.
-==Transformada de Fourier no tempo discreto (TFTD)==
+==Transformada de Fourier de tempo discreto (TFTD)==
 O sinal  <math> \mathrm{x(n)} </math> é discreto no tempo, e o sinal <math> \mathrm{X(\Omega)} </math> é contínuo e periódico em <math> \mathrm{2 \pi} </math>.
@@ Linha 65: / Linha 81: @@
 {{fig|2|Sinal discreto <math> \mathrm{x(n)} </math> e sua TFDT <math> \mathrm{X(e^{j\omega})} </math>| TFDTPlot.png| 800 px |}}
+==Série de Fourier de tempo contínuo (SF)==
+O sinal  <math> \mathrm{x(t)} </math> é contínuo e periódico no tempo (com período <math> T </math>) , e o sinal <math> \mathrm{X(k)} </math> é discreto na frequência.
+;A equação de análise: É uma transformação de um domínio de uma variável real <math> \mathrm{x(t)} </math> de tempo continuo em uma variável complexa <math> \mathrm{X(k)} </math> de frequência discreta.
+:<math>\mathrm{\ DT \rightarrow DF}</math>.
+:<math>\mathrm{x: \mathbb{R}\rightarrow\mathbb{C}}</math>.
+:<math> X(k)=\frac{1}{T}\int_{0}^{T}x(t)e^{-j(2\pi/T)kt)}\mathrm{d}t</math>
+;A equação de síntese: É uma transformação de um domínio de uma variável complexa <math> \mathrm{X(k)} </math> de frequência contínua em uma variável real <math> \mathrm{x(t)} </math> de tempo continuo.
+:<math>\mathrm{\ DF \rightarrow DT}</math>.
+:<math>\mathrm{X: \mathbb{C}\rightarrow\mathbb{R}}</math>.
+:<math>x(t)=\sum_{k = -\infty}^{\infty}X(k)e^{j(2\pi/T)kt)}</math>
+:A série de Fourier <math> \mathrm{X(k)} </math>, indicada acima é a série exponencial onde as funções de base são exponenciais complexas <math> e^{-j \omega t} </math>, onde <math> \omega = (2\pi/T)k </math>.  Também existem as séries de Fourier usando funções de base senoidais e cossenoidais, as quais podem ser derivadas da série exponencial.
+{{fig|3|Sinal <math> \mathrm{x(t)} </math> periódico e sua série de Fourier <math> \mathrm{X(\Omega)} </math>| SerieFourierPlot.png| 800 px |}}
 ==Transformada de Discreta de Fourier (TDF)==
+''Discrete Fourier Transform (DFT)''.
 ===Obtenção da TDF a partir da amostragem da TFTD===
 Sinais discretos no tempo podem ser representados pela sua TFTD, que é uma função continua periódica em <math> \mathrm{2 \pi} </math> de <math> \mathrm{\omega} </math> :
-:<math display="block">\mathrm{X(e^{j\omega}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j\omega n}}</math>
+:<math>\mathrm{X(e^{j\omega}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j\omega n}}</math>
 Para que a mesma possa ser utilizada no processamento de sinais digitais é necessário que a variável frequência seja também discreta. Se amostrarmos uniformemente a frequência  <math> \mathrm{\omega} </math> em N amostras entre 0 e <math> \mathrm{2 \pi} </math> é possível obter a TDF (ou DFT - ''Discrete Fourier Transform'').  Assim se tomarmos N frequências  <math> \mathrm{\omega_k = (2 \pi /N)k} \ </math> com   <math> k \in\mathbb{Z} \ </math>, and <math> \mathrm{0 \le k \le N-1} \ </math>, obtemos o espectro amostrado uniformemente:
-:<math display="block">\mathrm{X'(e^{j\omega}) = X(e^{j\omega}) \sum_{k= -\infty}^{\infty} \delta \left(\omega - \frac{2 \pi} {N}k \right)}</math>.
+:<math>\mathrm{X'(e^{j\omega}) = X(e^{j\omega}) \sum_{k= -\infty}^{\infty} \delta \left(\omega - \frac{2 \pi} {N}k \right)}</math>.
+:<math>\mathrm{X'(e^{j\omega}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j\frac{2 \pi} {N} k n}}</math>
 O sinal equivalente no tempo pode ser obtido aplicando a transformada inversa e a convolução:
-:<math display="block">\mathrm{x'(n) = \mathcal{F}^{-1}\{X'(e^{j\omega})\} =
+:<math>\mathrm{x'(n) = \mathcal{F}^{-1}\{X'(e^{j\omega})\} =
 x(n) * \left( \frac{N}{2 \pi} \sum_{p= -\infty}^{\infty} \delta (n-N p) \right) =
 \frac{N}{2 \pi} \sum_{p= -\infty}^{\infty} x(n-N p)}
@@ Linha 86: / Linha 126: @@
 *Se o comprimento L o sinal do <math> \mathrm{x(n)} \ </math> for maior que N o período de repetição do sinal <math> \mathrm{x'(n)} \ </math>, haverá sobreposição das amostras no tempo (''time aliasing''), e não será possível recuperar o sinal original.
 *Por outro lado, se <math> \mathrm{L \le N} \ </math> então <math> \mathrm{x'(n)} \ </math> é a repetição periódica  exata de <math> \mathrm{x(n)} \ </math>.
-:<math display="block">\mathrm{x(n) = \frac{2 \pi}{N} x'(n)} </math> , para <math> \mathrm{0 \le n \le N-1} \ </math> ou
+:<math>\mathrm{x(n) = \frac{2 \pi}{N} x'(n)} </math> , para <math> \mathrm{0 \le n \le N-1} \ </math> ou
-:<math display="block">\mathrm{x(n) = \frac{2 \pi}{N} x'(n)} [u(n)- u(n-N) \ </math>.
+:<math>\mathrm{x(n) = \frac{2 \pi}{N} x'(n)} [u(n)- u(n-N) \ </math>.
 Portanto, é possível recuperar as amostras do sinal digital no tempo <math> \mathrm{x(n)} \ </math> a partir das suas amostras digitais na frequência, desde que o período de repetição das N amostras de frequência seja maior ou igual ao comprimento L do sinal no tempo.
-===DFT e IDFT===
+===TDF e TDFI===
-*O sinal  <math> \mathrm{x(n)} \ </math> é discreto no tempo pode ser representado pelo o sinal <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> discreto e periódico em <math> \mathrm{2 \pi} \ </math>.
+O sinal  <math> \mathrm{x(n)} \ </math> é discreto no tempo pode ser representado pelo o sinal <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> ou <math> X(k) \ </math> discreto e periódico em <math> \mathrm{2 \pi} \ </math>.
 Para obter a equação de análise (DFT) pode ser feito o cálculo das amostras do espectro de frequências em  <math> \mathrm{\omega_k = (2 \pi /N)k} \ </math>   em:
-:<math display="block">\mathrm{X(e^{j\omega}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j\omega n}}</math>
+:<math>\mathrm{X(e^{j\omega}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j\omega n}}</math>
-:<math display="block">\mathrm{X(e^{j(2 \pi /N)k}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j(2 \pi /N)k n}}</math>
+:<math>\mathrm{X(e^{j(2 \pi /N)k}) = \sum_{n= -\infty}^{\infty} x(n) e^{-j(2 \pi /N)k n}}</math>
 Conforme mostrado, o espectro é periódico em N, e portanto é suficiente calcular apenas os valores para <math> \mathrm{0 \le k \le N-1} \ </math>.  Assim obtém-se
-;A equação de análise (DFT): É uma transformação de um domínio de uma variável real <math> \mathrm{x(n)} \ </math> de tempo discreto em uma variável complexa <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> frequência discreta periódica.
+;A equação de análise (TDF): É uma transformação de um domínio de uma variável real <math> \mathrm{x(n)} \ </math> de tempo discreto em uma variável complexa <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> frequência discreta periódica.
 :<math>\mathrm{\ DT \rightarrow DF}</math>.
 :<math>\mathrm{x: \mathbb{R}\rightarrow\mathbb{C}}</math>.
-:<math display="block">\mathrm{X(e^{j(2 \pi /N)k}) \equiv \mathcal{F}\{x(n)\}\
+:<math>\mathrm{X(e^{j(2 \pi /N)k}) \equiv \mathcal{F}\{x(n)\}\
 \overset{\underset{\mathrm{def}}{}}{=} \sum_{n= 0}^{N-1} x(n)\
 e^{-j(2 \pi /N)k n}}</math> , para <math> \mathrm{0 \le k \le N-1} \ </math>
-;A equação de síntese (IDFT): É uma transformação de um domínio de uma variável complexa <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> de frequência discreta periódica em uma variável real <math> \mathrm{x(n)} \ </math> discreta.
+;A equação de síntese (TDFI): É uma transformação de um domínio de uma variável complexa <math> \mathrm{X(e^{j(2 \pi /N)k})} \ </math> de frequência discreta periódica em uma variável real <math> \mathrm{x(n)} \ </math> discreta.
 :<math>\mathrm{\ DF \rightarrow DT}</math>.
 :<math>\mathrm{X: \mathbb{C}\rightarrow\mathbb{R}}</math>.
-:<math display="block">\mathrm{x(n) \equiv \mathcal{F}^{-1}\{X(e^{j(2 \pi /N)k})\}\
+:<math>\mathrm{x(n) \equiv \mathcal{F}^{-1}\{X(e^{j(2 \pi /N)k})\}\
 \overset{\underset{\mathrm{def}}{}}{=} \frac{1}{N}\sum_{k= 0}^{N-1}X(e^{j(2 \pi /N)k})\
 e^{j(2 \pi /N)k n} }</math> , para <math> \mathrm{0 \le n \le N-1} \ </math>
@@ Linha 118: / Linha 159: @@
 Ao usar a equação de análise, se o comprimento L de  <math> \mathrm{x(n)} \ </math> for menor que o período de repetição N, é necessário que <math> \mathrm{x(n)} \ </math>  seja preenchido com amostras nulas até atingir o comprimento N (''zero-padding'').
-;Simplificação da notação:
+=== Equação simplificada da TDF e TDFI===
-Para simplificar a notação é frequente utilizar:
+Para simplificar a notação pode-se utilizar para representar as frequência discreta:
-:<math> \mathrm{X(k) = X(e^{j(2 \pi /N)k})} \ </math> para a frequência discreta periódica.
+:<math> \mathrm{X(k) = X(e^{j(2 \pi /N)k})} \ </math>,
-E ainda definir:
-:<math> \mathrm{W_N = e^{-j2 \pi /N}} \ </math>
+definir a frequência fundamental <math> \omega_N \ </math> como:
-o qual representa um segmento <math> 1/N </math> do circulo unitário no plano complexo. Assim termos por exemplo que:
+:<math> \omega_N = e^{-j2 \pi /N} \ </math>
-:<math> \mathrm{W_1 = e^{-j2 \pi}} = +1 \ </math>
-:<math> \mathrm{W_{-1} = e^{j2 \pi}} = +1 \ </math>
+então
-:<math> \mathrm{W_2 = e^{-j \pi}} = -1 \ </math>
+:<math> e^{-j(2 \pi /N)k} = \omega_N^k \ </math>
-:<math> \mathrm{W_{-2} = e^{j \pi}} = -1 \ </math>
-:<math> \mathrm{W_4 = e^{-j \pi/2}} = -j \ </math>
+Essa frequência corresponde a uma posição no circulo unitário do plano complexo <math> z \ </math>.
-:<math> \mathrm{W_{-4} = e^{j \pi/2}} = +j \ </math>
+Alguns valores de <math> \omega_N \ </math> que ajudam a lembrar as simplificações:
+:<math> \omega_1 = e^{-j2 \pi} = +1 \ </math>
+:<math> \omega_{-1} = e^{j2 \pi} = +1 \ </math>
+:<math> \omega_2 = e^{-j \pi} = -1 \ </math>
+:<math> \omega_{-2} = e^{j \pi} = -1 \ </math>
+:<math> \omega_4 = e^{-j \pi/2} = -j \ </math>
+:<math> \omega_{-4} = e^{j \pi/2} = +j \ </math>
 Também é importante lembrar que se <math> N \ </math> é múltiplo de  <math> k \ </math> então:
-::<math> \mathrm{W_N^k = e^{-j(2 \pi /N)k} = e^{-j2 \pi /(N/k)} = W_{N/k}} \ </math>
+::<math> \omega_N^k = e^{-j(2 \pi /N)k} = e^{-j2 \pi /(N/k)} = \omega_{N/k} \ </math>
-Dessa forma as equações da DFT e IDFT passam a ser escritas de forma simplificada como:
+Dessa forma as equações da TDF e TDFI passam a ser escritas de forma simplificada como:
+;Equação de análise:
+:<math>\mathrm{X(k) = \sum_{n= 0}^{N-1} x(n) \omega_N^{kn}}</math> , para <math> \mathrm{0 \le k \le N-1} \ </math>
-:<math display="block">\mathrm{X(k) = \sum_{n= 0}^{N-1} x(n) W_N^{kn}}</math> , para <math> \mathrm{0 \le k \le N-1} \ </math>
+;Equação de síntese:
+:<math>\mathrm{x(n) = \frac{1}{N}\sum_{k= 0}^{N-1} X(k) \omega_N^{-kn}}</math> , para <math> \mathrm{0 \le n \le N-1} \ </math>
-:<math display="block">\mathrm{x(n) = \frac{1}{N}\sum_{k= 0}^{N-1} X(k) W_N^{-kn}}</math> , para <math> \mathrm{0 \le n \le N-1} \ </math>
+Dessas equações é possível perceber que o cálculo da TDF e da TDFI requerem a <math> \mathrm{N^2} \ </math> multiplicações e <math> \mathrm{N(N-1)} \ </math> somas, sendo portanto um algoritmo de <math> \mathrm{O(N^2)} \ </math>.
-Dessas equações é possível perceber que o cálculo da DFT e da IDFT requerem a <math> \mathrm{N^2} \ </math> multiplicações e <math> \mathrm{N(N-1)} \ </math> somas, sendo portanto um algoritmo de <math> \mathrm{O(N^2)} \ </math>.
+=== Notação matricial de TDF e TDFI===
+Em notação matricial cada <math> X(k) \ </math> na TDF e <math> x(k) \ </math> na TDFI podem ser calculado como:
+:<math> X(k)
+=
+\begin{bmatrix}
+\omega_N^0 & \omega_N^{k} & \omega_N^{2k} & ... & \omega_N^{(N-1)k}\\
+\end{bmatrix}
+\times
+\begin{bmatrix}
+x(0)\\
+x(1)\\
+x(2)\\
+\vdots \\
+x(N-1)\end{bmatrix}
+</math>
+:<math> x(k)
+=\frac{1}{N}
+\begin{bmatrix}
+\omega_N^0 & \omega_N^{-k} & \omega_N^{-2k} & ... & \omega_N^{-(N-1)k}\\
+\end{bmatrix}
+\times
+\begin{bmatrix}
+X(0)\\
+X(1)\\
+X(2)\\
+\vdots \\
+X(N-1)\end{bmatrix}
+</math>
+Porém como <math> \omega_N^0 = 1 </math> as equações TDF e TDFI podem ser escritas em notação matricial:
+;Equação de análise:
+:<math> \begin{bmatrix}
+X(0) \\
+X(1) \\
+X(2) \\
+\vdots \\
+X(N-1)
+\end{bmatrix} =
+\begin{bmatrix}
+& 1 & 1 & ... & 1 \\
+& \omega_N^1 & \omega_N^2 & ... & \omega_N^{(N-1)} \\
+& \omega_N^2 & \omega_N^4 & ... & \omega_N^{2(N-1)} \\
+\vdots & \vdots & \vdots & \ddots & \vdots\\
+& \omega_N^{(N-1)} & \omega_N^{2(N-1)} & ... & \omega_N^{(N-1)^2} \\
+\end{bmatrix}
+\times
+\begin{bmatrix}
+x(0) \\
+x(1) \\
+x(2) \\
+\vdots \\
+x(N-1)\end{bmatrix} </math>
+;Equação de síntese:
+:<math> \begin{bmatrix}
+x(0) \\
+x(1) \\
+x(2) \\
+\vdots \\
+x(N-1)
+\end{bmatrix}
+=\frac{1}{N}
+\begin{bmatrix}
+& 1 & 1 & ... & 1 \\
+& \omega_N^{-1} & \omega_N^{-2} & ... & \omega_N^{-(N-1)} \\
+& \omega_N^{-2} & \omega_N^{-4} & ... & \omega_N^{-2(N-1)} \\
+\vdots & \vdots & \vdots & \ddots & \vdots\\
+& \omega_N^{-(N-1)} & \omega_N^{-2(N-1)} & ... & \omega_N^{-(N-1)^2} \\
+\end{bmatrix}
+\times
+\begin{bmatrix}
+X(0) \\
+X(1) \\
+X(2) \\
+\vdots \\
+X(N-1)\end{bmatrix} </math>
 === Transformada Rápida de Fourier (FFT) ===
-As FFTs são algoritmos que reduzem a complexidade do cálculo da DFT, obtendo ordens de <math> \mathrm{ O(log N \times N)} \ </math>.
+O cálculo da TDF e TDFI para uma sequência de dados de comprimento <math> N \ </math> necessita de <math> N^2 \ </math> multiplicações complexas, limitando o seu uso em aplicações práticas.  Em 1965, [https://www.ams.org/journals/mcom/1965-19-090/S0025-5718-1965-0178586-1/S0025-5718-1965-0178586-1.pdf Cooley e Tukey] propuseram um algoritmo rápido (FFT) para calcular a TDF com um número de multiplicações complexas na ordem de <math> \mathrm{ O(N \times log_2N)} \ </math>.  Esse mudança faz com que uma sequência de comprimento 1024, calculado com a TDF demanda 1024x1024 multiplicações, enquanto que com a FFT apenas 1024x10.  Isso representa neste caso uma redução de complexidade de 100 vezes.
+Atualmente existem diversos algoritmos de FFT, que obtêm exatamente o mesmo valor que o uso da TDF, mas eles podem ser classificados de forma geral em decimação no tempo, ou decimação na frequência, dependendo de qual vetor será decimado e reordenado, se o sinal no tempo <math> x(n) \ </math>  ou as frequencia <math> X(k) \ </math>.
+Ver este e-book [https://cnx.org/exports/d2c6d393-3590-403d-8a18-c892055b046b@2.2.pdf/the-dft-fft-and-practical-spectral-analysis-2.2.pdf  The  DFT, FFT, and Practical Spectral Analysis] em OpenStax CNX, e também a [https://en.wikipedia.org/wiki/Cooley%E2%80%93Tukey_FFT_algorithm wikipedia] que tem esse artigo muito bem escrito sobre o assunto.
+*Para relembrar os conceitos vistos acima, recomendo assistir os vídeos sobre DFT e FFT do prof. Steve Brunton da University of Washington
+{| class="wikitable"
+|-
+! The Discrete Fourier Transform (DFT)
+! Computing the DFT Matrix
+! The Fast Fourier Transform (FFT)
+! The Fast Fourier Transform Algorithm
+| What is a Fast Fourier Transform (FFT)?
+|-
+|{{#ev:youtube|nl9TZanwbBk|300}}
+|{{#ev:youtube|Xw4voABxU5c|300}}
+|{{#ev:youtube|E8HeD-MUrjY|300}}
+|{{#ev:youtube|toj_IoCQE-4|300}}
+|{{#ev:youtube|XtypWS8HZco|300}}
+|}
 == Soma dos termos de uma Progressão Geométrica ==

Transformadas de Fourier: mudanças entre as edições

Edição atual tal como às 15h58min de 19 de novembro de 2020

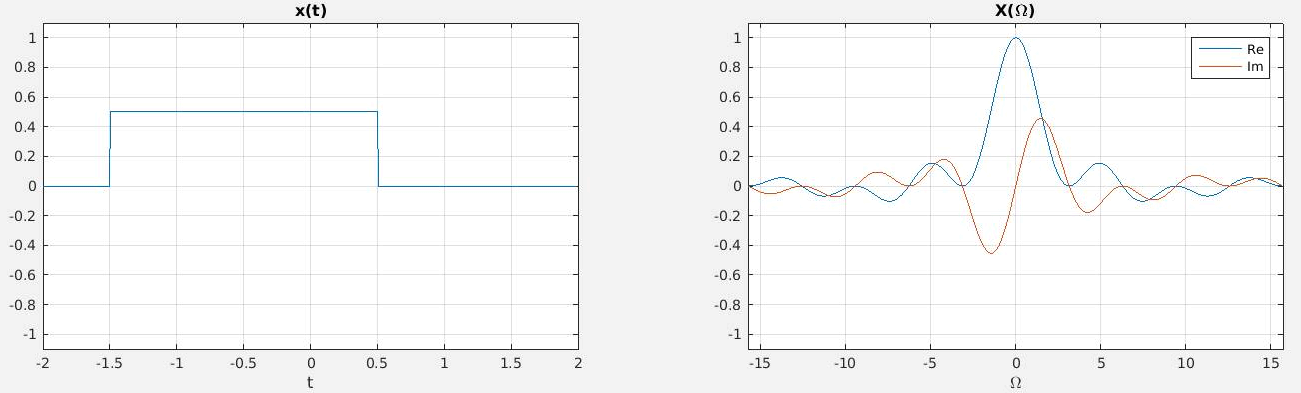
1 Transformada de Fourier no tempo contínuo (TFTC)

2 Transformada Z

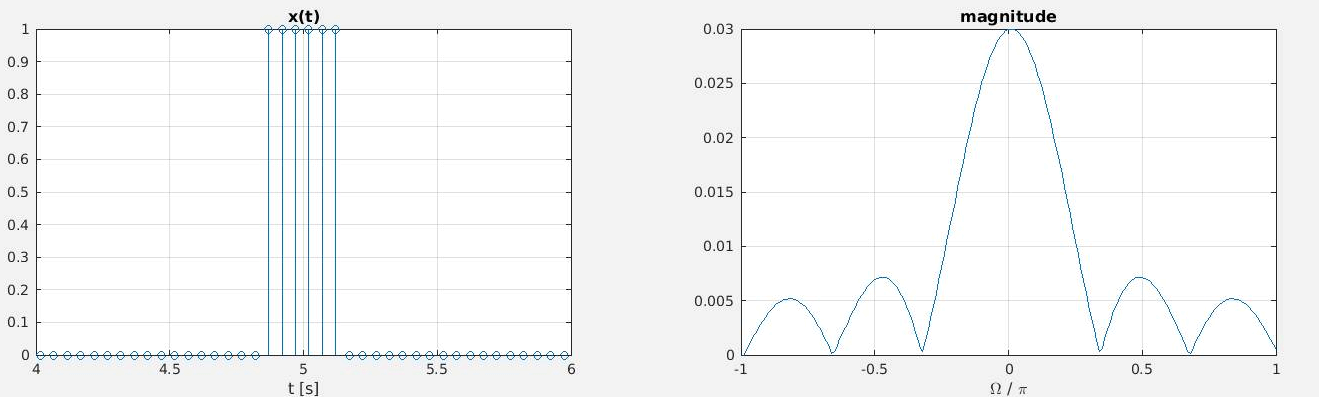
3 Transformada de Fourier de tempo discreto (TFTD)

4 Série de Fourier de tempo contínuo (SF)

5 Transformada de Discreta de Fourier (TDF)

5.1 Obtenção da TDF a partir da amostragem da TFTD

5.2 TDF e TDFI

5.3 Equação simplificada da TDF e TDFI

5.4 Notação matricial de TDF e TDFI

5.5 Transformada Rápida de Fourier (FFT)

6 Soma dos termos de uma Progressão Geométrica

Menu de navegação

Pesquisa