Transformação Bilinear: mudanças entre as edições
| Linha 17: | Linha 17: | ||
&= \frac{2}{T} \left[\frac{z-1}{z+1} + \frac{1}{3} \left( \frac{z-1}{z+1} \right)^3 + \frac{1}{5} \left( \frac{z-1}{z+1} \right)^5 + \frac{1}{7} \left( \frac{z-1}{z+1} \right)^7 + \cdots \right] \\ | &= \frac{2}{T} \left[\frac{z-1}{z+1} + \frac{1}{3} \left( \frac{z-1}{z+1} \right)^3 + \frac{1}{5} \left( \frac{z-1}{z+1} \right)^5 + \frac{1}{7} \left( \frac{z-1}{z+1} \right)^7 + \cdots \right] \\ | ||
&\approx \frac{2}{T} \frac{z - 1}{z + 1} \\ | &\approx \frac{2}{T} \frac{z - 1}{z + 1} \\ | ||
& | &\approx \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Linha 31: | Linha 31: | ||
\begin{align} | \begin{align} | ||
z &= e^{sT} \\ | z &= e^{sT} \\ | ||
&\approx \frac{1 + s T / 2}{1 - s T / 2} | &\approx \frac{1 + s T / 2}{1 - s T / 2} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
{{collapse_top | Demonstração}} | |||
:<math> | |||
\begin{align} | |||
&z = e^{sT} \\ | |||
\text{foi visto que} \\ | |||
&s \approx \frac{2}{T} \frac{z - 1}{z + 1} \\ | |||
\text{então rearranjando z} \\ | |||
&s T / 2(z + 1) \approx (z - 1) \\ | |||
&(s T / 2) z + s T / 2 \approx z - 1 \\ | |||
&1 + s T / 2 \approx z(1 - s T / 2) \\ | |||
\text{portanto} \\ | |||
&z \approx \frac{1 + s T / 2}{1 - s T / 2} | |||
\end{align} | |||
</math> | |||
{{collapse_bottom}} | |||
== Empenamento de frequência (''frequency warping'') == | == Empenamento de frequência (''frequency warping'') == | ||
Edição atual tal como às 13h30min de 23 de abril de 2020
1 Discretização de filtros analógicos
A transformação bilinear do domínio da Transformada de Laplace para o domínio da Transformada z é feito por
O mapeamento inverso em é feita por
é uma aproximação de primeira ordem do logaritmo pela série de potência
Essa transformação é o resulta em um mapeamento exato do plano z no plano s através de
| Demonstração |
|---|
|
|
Ela pode ser utilizada para ser transformar um sistema linear invariante no tempo continuo (filtro analógico) em um sistema linear invariante no tempo discreto (filtro digital) , e vice-versa. O mapeamento da função em é feita por:
O mapeamento inverso em é feita pela aproximação de primeira ordem da substituição
| Demonstração |
|---|
|
|
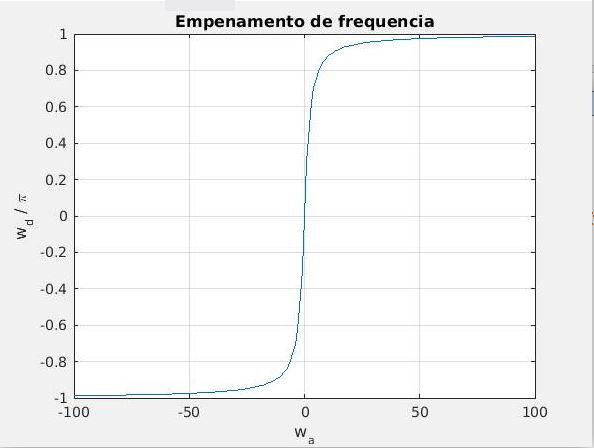
2 Empenamento de frequência (frequency warping)
Determinar a resposta de frequência em filtro analógico (de tempo contínuo), a função de transferência é avaliada em , que corresponde aos valores dessa função no eixo imaginário . Da mesma forma para filtros digitais (de tempo discreto), a função de transferência é avaliada em , correspondendo aos valores sobre o circulo unitário pois possui magnitude constante .
A transformação bilinear mapeia o eixo imaginário do plano s no circulo unitário no plano z, no entanto o mapeamento das frequências não é linear, sofrendo um empenamento (distorção). Para utilizar essa transformação na obtenção de filtros digitais a partir de filtros analógicos, é necessário determinar como cada frequencia do filtro final desejado deve ser projetada no filtro analógico . Essa distorção pode ser obtida fazendo a substituição de na equação da transformação bilinear, e aplicando a fórmula de Euler para o seno.
| Demonstração | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Considere que: e que
|
Isso mostra que cada ponto no circulo unitário do plano z é mapeado em um ponto no eixo imaginário do plano s. E que as frequências do filtro digital são mapeadas nas frequencias analógicas pela equação:
Além disso a faixa infinita de frequências do filtro analógico
é mapeada no filtro digital no intervalo limitado