FIC MATLAB 2018-2: mudanças entre as edições
| (58 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 14: | Linha 14: | ||
:'''Referência Complementar:''' MORAIS, V.. VIEIRA, C. '''MATLAB Curso Completo'''. FCA, 2013. 644. ISBN 9727227058 | :'''Referência Complementar:''' MORAIS, V.. VIEIRA, C. '''MATLAB Curso Completo'''. FCA, 2013. 644. ISBN 9727227058 | ||
:'''Tutorial''': [http://mtm.ufsc.br/~palomino/arquivos/matlab.pdf Bernardo Severo da Silva Filho, Curso de MATLAB 5.1] | |||
== Conteúdos Abordados == | == Conteúdos Abordados == | ||
=== 1 - Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição === | |||
=== Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais === | {{collapse top| bg=lightblue | 11/Set - }} | ||
{{collapse top| bg=lightblue | 11/Set}} | |||
* MATLAB e Octave; | * MATLAB e Octave; | ||
| Linha 107: | Linha 108: | ||
:::<math>d = \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)}</math> | :::<math>d = \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)}</math> | ||
:::<math> | :::<math>d = 5{,}2 \cos^2 \left( \frac{x + y}{e^{\frac{x}{y}} \log_{10}(\pi)} \right)</math> | ||
* Ajudas: | * Ajudas: | ||
| Linha 132: | Linha 134: | ||
| NaN || Indica um resultado numérico indefinido. | | NaN || Indica um resultado numérico indefinido. | ||
|} | |} | ||
* Formatos de exibição: | * Formatos de exibição: | ||
:::{| class="wikitable" | :::{| class="wikitable" | ||
| Linha 165: | Linha 159: | ||
| format loose || Restabelece o modo de exibição menos compacto | | format loose || Restabelece o modo de exibição menos compacto | ||
|} | |} | ||
* [[FIC_MATLAB_2018-2/Aula-1|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 2 - Vetores e matrizes === | |||
{{collapse top| bg=lightblue | 13/Set}} | |||
| Linha 182: | Linha 185: | ||
:1. Crie os vetores descritos abaixo usando dois métodos diferentes: | :1. Crie os vetores descritos abaixo usando dois métodos diferentes: | ||
::a) Início: 5, Fim: 28, com 100 elementos regularmente espaçados | ::a) Início: 5, Fim: 28, com 100 elementos regularmente espaçados. | ||
::b) Início: 5, Fim: 14, com passo de 0,2. | ::b) Início: 5, Fim: 14, com passo de 0,2. | ||
::c) Início: -2, Fim: 5, com 50 elementos regularmente espaçados | ::c) Início: -2, Fim: 5, com 50 elementos regularmente espaçados. | ||
::d) Início: 100, Fim: 12, com 100 elementos regularmente espaçados | ::d) Início: 100, Fim: 12, com 100 elementos regularmente espaçados. | ||
:2. Crie os vetores descritos abaixo: | :2. Crie os vetores descritos abaixo: | ||
::a) Início: 10, Fim: 1000, com 50 elementos logaritmicamente espaçados | ::a) Início: 10, Fim: 1000, com 50 elementos logaritmicamente espaçados. | ||
::b) Início: 0,01, Fim: 1, com 20 elementos logaritmicamente espaçados | ::b) Início: 0,01, Fim: 1, com 20 elementos logaritmicamente espaçados. | ||
:3. Crie um vetor '''x''' que tenha 6 valores entre 0 e 10. Em seguida, crie uma matriz '''A''' cuja primeira linha contenha os valores 3'''x''' e segunda linha contenha os valores 5'''x''' - 20. | :3. Crie um vetor '''x''' que tenha 6 valores entre 0 e 10. Em seguida, crie uma matriz '''A''' cuja primeira linha contenha os valores 3'''x''' e segunda linha contenha os valores 5'''x''' - 20. | ||
:4. Repita o exercício anterior, substituindo a palavra ''linha'' por ''coluna''. | :4. Repita o exercício anterior, substituindo a palavra ''linha'' por ''coluna''. | ||
:5. Crie o vetor ''v = [2 4 8 16 32 ... 512 1024]'' utilizando o comando ''logspace''. | |||
| Linha 206: | Linha 211: | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Operações com matrizes; Plots === | === 3 - Operações com matrizes; Plots === | ||
{{collapse top| bg=lightblue | 18/Set}} | {{collapse top| bg=lightblue | 18/Set}} | ||
| Linha 271: | Linha 277: | ||
::e) X<sup>2</sup> | ::e) X<sup>2</sup> | ||
::f) B C (multiplicação elemento a elemento) | ::f) B C (multiplicação elemento a elemento) | ||
:3. Crie o vetor ''v = [1 4 9 16 25 ... 81 100]''. | |||
:4. Crie o vetor ''v = [2 4 8 16 32 ... 512 1024]'' sem utilizar o comando ''logspace''. | |||
:5. Utilize o MATLAB para calcular 12! (isto é, o fatorial do número 12), sem utilizar o comando ''factorial''. | |||
:6. O [https://pt.wikipedia.org/wiki/S%C3%A9rie_harm%C3%B3nica_(matem%C3%A1tica) número harmônico] <math>H_n</math> é definido como sendo a soma ''1 + 1/2 + ... + 1/n''. Utilize o MATLAB para calcular <math>H_{100}</math>. ''Resposta: 5.1874.'' | |||
:7. Seja | |||
:::::<math> | |||
x = 1 + 1/4 + 1/9 + 1/16 + 1/25 + \cdots + 1/10000^2. | |||
</math> | |||
::Calcule ''x''. Em seguida, calcule <math>\sqrt{6x}</math>. ''Resposta: Aproximadamente <math>\pi</math>.'' | |||
| Linha 351: | Linha 372: | ||
* '''Exercícios''' | * Outros comandos relacionados a plotagem: | ||
:* Comando ''figure'' | |||
:* Comando ''subplot'' | |||
:* Comando ''close all'' para fechar todas figuras | |||
* [[FIC_MATLAB_2018-2/Aula-3|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 4 - Aula de exercícios === | |||
{{collapse top| bg=lightblue | 20/Set}} | |||
* '''Exercícios''' (Plots) | |||
:1. | :1. Plote, em um mesmo gráfico, as funções | ||
:::::<math>f(x) = \sqrt{1 - (|x| - 1)^2}</math> | |||
::e | |||
:::::<math>\displaystyle{g(x) = \arccos(1 - |x|) - \pi},</math> | |||
::para <math>-2 \leq x \leq 2</math>. | |||
:2. | :2. Plote a função <math>\displaystyle{f(x) = x^2 + x - 2}</math> de -4 até 4 e encontrar as raízes por Bhaskara. | ||
:3. Utilize o MATLAB para plotar a função <math>T = 3 \ln (2 t) - 5 e^{0,5 t}</math> ao longo do intervalo <math>1 \leq t \leq 3</math>. Insira um título na plotagem e rotule adequadamente os eixos. A variável ''T'' representa a temperatura em graus Celsius; a variável ''t'' representa o tempo em minutos. | :3. Utilize o MATLAB para plotar a função <math>\displaystyle{T = 3 \ln (2 t) - 5 e^{0,5 t}}</math> ao longo do intervalo <math>1 \leq t \leq 3</math>. Insira um título na plotagem e rotule adequadamente os eixos. A variável ''T'' representa a temperatura em graus Celsius; a variável ''t'' representa o tempo em minutos. | ||
:4. Plote as funções <math>u = 100 \log_{10} (60 x + 1)</math> e <math>v = 50 \cos(6 x) \mathrm{sen} (2 x) + 150 x</math> ao longo do intervalo <math>0 \leq x \leq 2</math>. Rotule adequadamente a plotagem e cada uma das curvas, utilizando '''legend'''. A variável ''u'' representa a velocidade de uma Ferrari em km/h. A variável ''v'' representa a velocidade de um Fusca. | :4. Plote as funções <math>\displaystyle{u = 100 \log_{10} (60 x + 1)}</math> e <math>\displaystyle{v = 50 \cos(6 x) \mathrm{sen} (2 x) + 150 x}</math> ao longo do intervalo <math>0 \leq x \leq 2</math>. Rotule adequadamente a plotagem e cada uma das curvas, utilizando '''legend'''. A variável ''u'' representa a velocidade de uma Ferrari em km/h. A variável ''v'' representa a velocidade de um Fusca. | ||
:5. Use a função ''stem'' para plotar os sinais abaixo na mesma figura: | :5. Use a função ''stem'' para plotar os sinais abaixo na mesma figura: | ||
:: <math>\cos(x)</math>, para <math>0 \leq x \leq 2 \pi</math> | :: <math>\displaystyle{\cos(x)}</math>, para <math>0 \leq x \leq 2 \pi</math> | ||
:: <math>0,5 \sin(x)</math>, para <math>\pi \leq x \leq 3 \pi</math> | :: <math>\displaystyle{0,5 \sin(x)}</math>, para <math>\pi \leq x \leq 3 \pi</math> | ||
:6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função | :6. A série de Fourier é uma representação em série de funções periódicas em termos de senos e cossenos. A representação em série de Fourier da função | ||
| Linha 373: | Linha 412: | ||
::é | ::é | ||
:::::<math>g(x) = \frac{4}{\pi} \left( \frac{\sin(x)}{1} + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5} + \frac{\sin(7x)}{7} + \cdots \right)</math>. | :::::<math>g(x) = \frac{4}{\pi} \left( \frac{\sin(x)}{1} + \frac{\sin(3x)}{3} + \frac{\sin(5x)}{5} + \frac{\sin(7x)}{7} + \cdots \right)</math>. | ||
::Plote em um mesmo gráfico a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando os quatro termos explicitados. | ::Plote, em um mesmo gráfico, a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando os quatro termos explicitados. Considere ''x'' na faixa de <math>-\pi</math> até <math>\pi</math>. | ||
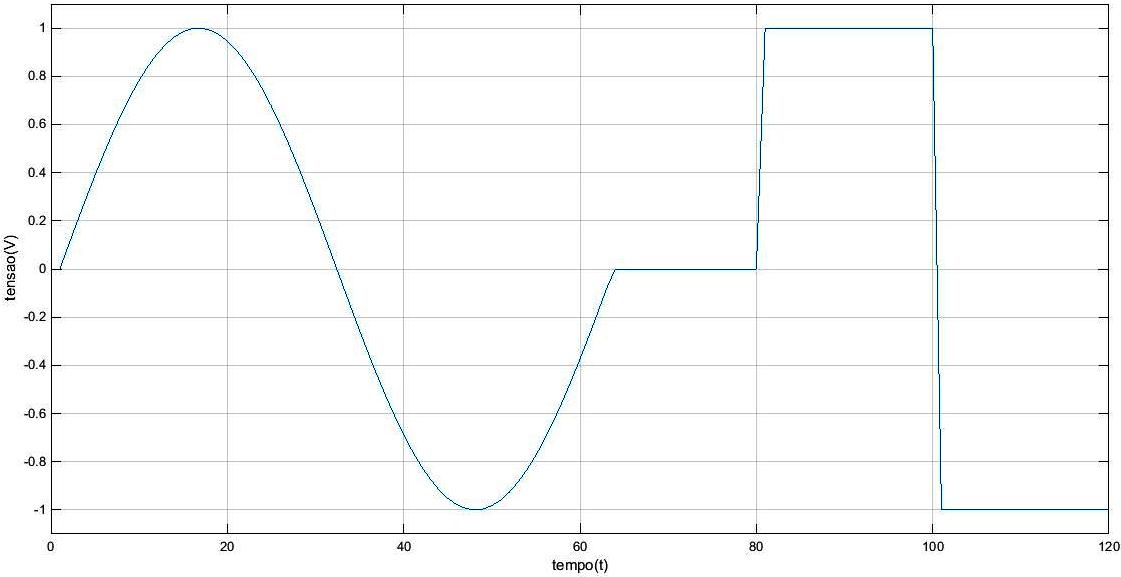
:7. Fazer o ''plot'' de um sinal de tensão versus tempo, como da figura: | :7. Fazer o ''plot'' de um sinal de tensão versus tempo, como da figura: | ||
| Linha 387: | Linha 426: | ||
* [[FIC_MATLAB_2018-2/Aula- | * [[FIC_MATLAB_2018-2/Aula-4|Gabarito]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== | === 5 - Endereçamento de vetores e matrizes === | ||
{{collapse top| bg=lightblue | | {{collapse top| bg=lightblue | 25/Set}} | ||
* Endereçamento de vetores e matrizes | * Endereçamento de vetores e matrizes | ||
| Linha 418: | Linha 446: | ||
* '''Exercícios:''' | * [[FIC_MATLAB_2018-2/Aula-5|Códigos executados na aula]] | ||
{{collapse bottom}} | |||
=== 6 - Concatenação de matrizes; Texto; Entrada e saída de dados; Conjuntos; Polinômios; Números aleatórios === | |||
{{collapse top| bg=lightblue | 27/Set}} | |||
* Concatenação de vetores e matrizes | |||
* Comandos ''repmat'', ''reshape'', ''fliplr'' e ''flipud'' | |||
* Trabalhando com texto (''string'') | |||
* Entrada/Saída de dados | |||
:* Comando ''input'' para entrada de dados | |||
:* Comando ''disp'' para saída de dados | |||
:* Comandos ''num2str'' e ''str2num'' | |||
:* Entrada de dados sem a tecla ENTER | |||
* '''Exercício''': | |||
:1. Criar uma calculadora de IMC com perguntas (''input'') para massa e altura. Use o ''disp'' para exibir o resultado de forma ''agradável'' ao usuário. | |||
* Conjuntos | |||
:* Comandos ''sort'', ''unique'' | |||
:* Comandos ''union'' (<math>A \cup B</math>), ''intersect'' (<math>A \cap B</math>), ''setdiff'' (<math>A \setminus B</math>), ''setxor'' (diferença simétrica) | |||
* Polinômios | |||
:* Representação de polinômios a partir de vetores | |||
:* Comandos ''polyval'', ''poly'' e ''roots'' | |||
:* Comandos ''conv'' e ''deconv'' para multiplicação e divisão de polinômios | |||
:* Comandos ''polyder'' e ''polyint'' para derivada e integral de polinômios | |||
* Números aleatórios | |||
:* Comando ''randi'' para valores inteiros uniformemente distribuídos | |||
:* Comando ''rand'' para valores uniformemente distribuídos | |||
:* Comando ''randn'' para valores normalmente distribuídos | |||
:* Comando ''hist'' para cálculo/visualização do histograma | |||
* '''Exercícios''': | |||
:1. Mostre todos os inteiros positivos | |||
::a) menores que 100 que são múltiplos de 3 ou de 5. | |||
::b) menores que 200 que são múltiplos de 3 e 5. | |||
::c) menores que 125 que são múltiplos de 3 ou de 5, mas não de ambos. | |||
:2. Utilize o MATLAB para obter as raízes do polinômio | |||
:::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math>. | |||
::Utilize a função ''poly'' para confirmar sua resposta. | |||
:3. Utilize o MATLAB para confirmar que | |||
:::::<math>\displaystyle{(20x^3 - 7x^2 + 5x + 10)(4x^2 + 12x - 3) = 80x^5 + 212x^4 - 124x^3 + 121x^2 + 105x - 30}.</math> | |||
:4. Utilize o MATLAB para confirmar que | |||
:::::<math>\frac{12x^3 + 5x^2 - 2x + 3}{3x^2 - 7x + 4} = 4x + 11</math> | |||
::com resto de <math>\displaystyle{59x - 41}</math>. | |||
:5. Utilize o MATLAB para confirmar que | |||
:::::<math>\frac{6x^3 + 4x^2 - 5}{12x^3 - 7x^2 + 3x + 9} = 0{,}7108</math> | |||
::quando <math>x = 2</math>. | |||
:6. Plote o polinômio | |||
:::::<math>\displaystyle{x^3 + 13x^2 + 52x + 6}</math> | |||
::ao longo da faixa <math>-7 \leq x \leq 1</math>. | |||
* [[FIC_MATLAB_2018-2/Aula-6|Códigos executados na aula]] | |||
{{collapse bottom}} | |||
=== 7 - Aula de exercícios === | |||
{{collapse top| bg=lightblue | 02/Out}} | |||
* '''Exercícios (endereçamento):''' | |||
:1. Crie uma matriz '''A''' de tamanho 15 x 15 de inteiros. | :1. Crie uma matriz '''A''' de tamanho 15 x 15 de inteiros. | ||
| Linha 470: | Linha 574: | ||
::: A(3, :) = b([3 1 2]); | ::: A(3, :) = b([3 1 2]); | ||
* '''Exercícios''': | * '''Exercícios''': | ||
| Linha 502: | Linha 598: | ||
::Utilize o MATLAB para responder essas questões: | ::Utilize o MATLAB para responder essas questões: | ||
:::a) Quanto cada trabalhador recebeu na semana? | :::a) Quanto cada trabalhador recebeu na semana? | ||
:::b) Qual foi o salário total pago? | :::b) Qual foi o salário total pago na semana? | ||
:::c) Quantos dispositivos foram fabricados? | :::c) Quantos dispositivos foram fabricados na semana? | ||
:::d) Qual é o custo médio para se produzir um dispositivo? | :::d) Qual é o custo médio para se produzir um dispositivo? | ||
:::e) Quantas horas são necessárias, em média, para se produzir um dispositivo? | :::e) Quantas horas são necessárias, em média, para se produzir um dispositivo? | ||
| Linha 515: | Linha 611: | ||
::Crie uma figura contendo 3 plots: | ::Crie uma figura contendo 3 plots: | ||
::* A função seno | ::* A função seno verdadeira | ||
::* A aproximação de Bhaskara I | ::* A aproximação de Bhaskara I | ||
::* O erro da aproximação | ::* O erro da aproximação | ||
:3. Se uma bola | :3. Se uma bola é lançada da altura <math>h_0 = 28</math> m acima da superfície da terra, com velocidade vertical <math>v_0 = 20</math> m/s, a posição e a velocidade da bola como função no tempo serão dadas pelas equações | ||
:::<math> | :::<math>h(t) = \frac{1}{2} g t^2 + v_0 t + h_0</math> | ||
h(t) = \frac{1}{2} g t^2 + v_0 t + h_0 | :::<math>\displaystyle{v(t) = g t + v_0}</math> | ||
</math> | ::onde ''g'' é a aceleração da gravidade (-9,81 m/s²). A bola atingirá o solo em | ||
:::<math> | :::<math>t_\mathrm{hit} = -\frac{v_0 + \sqrt{v_0^2 - 2 g h_0}}{g}.</math> | ||
v(t) = g t + v_0 | ::Escreva um programa de MATLAB que desenhe a altura e a velocidade como função do tempo, para <math>0 \leq t \leq t_\mathrm{hit}</math> utilizando o comando ''subplot''. Faça com que <math>h_0</math> e <math>v_0</math> sejam parâmetros da script. Não deixe de incluir as legendas apropriadas. | ||
</math> | |||
::onde ''g'' é a aceleração da gravidade (-9,81 m/s²). Escreva um programa de MATLAB que desenhe a altura e a velocidade como função do tempo. Faça com que <math>h_0</math> e <math>v_0</math> sejam parâmetros da script. Não deixe de incluir as legendas apropriadas. | |||
:4. Joãozinho depositou <math>v_p = \text{BRL } 1.000,00</math> num fundo de investimento com taxa de juros <math>j = 0{,}8 %</math> ao mês. Faça um gráfico do saldo do investimento. Em quanto tempo o valor depositado será dobrado? Dica: [https://pt.wikipedia.org/wiki/Juro#Juros_compostos (link)] | :4. Joãozinho depositou <math>v_p = \text{BRL } 1.000,00</math> num fundo de investimento com taxa de juros <math>j = 0{,}8 %</math> ao mês. Faça um gráfico do saldo do investimento. Em quanto tempo o valor depositado será dobrado? Dica: [https://pt.wikipedia.org/wiki/Juro#Juros_compostos (link)] | ||
* ''' | |||
* '''Desafios''': | |||
:1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. | :1. Plote um círculo com raio 2 e centrado no ponto (4,3). Dica: use equações paramétricas. | ||
:2. Repita o Exercício 6 da Aula | :2. Repita o Exercício 6 da Aula 4 com um número genérico de termos <math>\sin()</math> somados em <math>g(x)</math>. | ||
:3. Plote o símbolo do Batman (para quem tem dúvida, [http:// | :3. Plote o símbolo do Batman (para quem tem dúvida, [http://guangchuangyu.github.io/blog_images/2011/08/X.png link]). | ||
* | * [[FIC_MATLAB_2018-2/Aula-7|Códigos executados na aula]] | ||
{{collapse bottom}} | |||
=== 8 - Variáveis lógicas; Operadores relacionais e lógicos === | |||
{{collapse top| bg=lightblue | 04/Out}} | |||
* | * Variáveis lógicas (''booleanas''): | ||
:* Comando ''logical'' | :* Comando ''logical'' | ||
| Linha 618: | Linha 667: | ||
|} | |} | ||
:* Operadores lógicos | :* Operadores lógicos: | ||
:::{| class="wikitable" | :::{| class="wikitable" | ||
| Linha 633: | Linha 682: | ||
|} | |} | ||
:* | :* Comparação de vetores ou matrizes: | ||
::* Comando ''isequal'' | |||
:: | |||
:* Comparação de ''strings'': | :* Comparação de ''strings'': | ||
| Linha 661: | Linha 702: | ||
:2. A tabela abaixo mostra as temperaturas diárias (em Celsius) em três cidades diferentes. | :2. A tabela abaixo mostra as temperaturas diárias (em Celsius) em três cidades diferentes. | ||
<center> | |||
! | {| class="wikitable" | ||
! colspan="8" style="text-align: center; font-weight:bold;" | Temperatura | |||
|- | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Cidade | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 1 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 2 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 3 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 4 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 5 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 6 | |||
| style="font-weight:bold; background-color:#c0c0c0;" | Dia 7 | |||
|- | |- | ||
| Palhoça || 10 || 13 || 6 || 5 || -1 || 10 || 4 | | Palhoça || 10|| 13|| 6|| 5|| -1|| 10|| 4 | ||
|- | |- | ||
| São José || 19 || 13 || 3 || 5 || 1 || 22 || 14 | | São José|| 19|| 13|| 3|| 5|| 1|| 22|| 14 | ||
|- | |- | ||
| Biguaçu || 30 || 2 || 3 || -1 || 10 || -2 || 40 | | Biguaçu|| 30|| 2|| 3|| -1|| 10|| -2|| 40 | ||
|} | |} | ||
</center> | |||
:Determine em quais dias: | :Determine em quais dias: | ||
| Linha 691: | Linha 736: | ||
::b) Determine os instantes de tempo em que a altura é de no mínimo 15 m. | ::b) Determine os instantes de tempo em que a altura é de no mínimo 15 m. | ||
::c) Determine os instantes de tempo em que a altura é de no mínimo 15 m e, ao mesmo tempo, a velocidade é de no máximo 36 m/s. | ::c) Determine os instantes de tempo em que a altura é de no mínimo 15 m e, ao mesmo tempo, a velocidade é de no máximo 36 m/s. | ||
:: | ::d) Determine os instantes de tempo em que a altura é de no mínimo 15 m ou a velocidade é de no máximo 36 m/s. | ||
::e) Destaque as figuras anteriores com os intervalos calculados na letra c). | |||
* [[FIC_MATLAB_2018-2/Aula-8|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 9 - Controle de fluxo de dados - ''if'' e ''switch'' === | |||
{{collapse top| bg=lightblue | 09/Out}} | |||
* Uso de scripts: | |||
:* Editor de texto (''Editor'') | |||
:* Seções (''%%'') | |||
:* ''Publish'' | |||
| Linha 701: | Linha 760: | ||
* '''Exercícios''': | * '''Exercícios''': | ||
:1. Crie um código que calcula o valor gasto total (em R$) e o peso total (em kg) da compra de algumas unidades de arroz (5 kg), feijão (1 kg) e café (500 g). | :1. Crie um programa que recebe do usuário um número ''X''. Se este número for maior que 10, então, o programa deve mostrar o quadrado do número ''X''. Caso contrário, o número ''X'' deve ser exibido junto com uma mensagem de boa noite. | ||
:2. Escreva um programa no qual o usuário irá entrar com uma ''string'', que irá informar o assunto de uma discussão em um bate-papo da UOL. O programa deverá mostrar uma mensagem de boas vindas relacionada ao tema nos casos em que o tema seja '''cinema''', '''moda''' ou '''gastronomia'''. Se o assunto for '''politica''', '''futebol''' ou '''religiao''', o programa deverá informar que estes assuntos estão proibidos. Qualquer outro assunto é inválido, e deverá receber uma mensagem crítica. | |||
:3. Escreva um programa no qual o usuário fornece três valores: o valor inicial, o valor final e o passo de um intervalo. Crie proteções para que o intervalo seja consistente. Por exemplo, se o valor final for menor que o valor inicial, então o passo deve ser negativo. Ao fim do programa, exiba <math>x^2</math>, onde ''x'' é o intervalo. | |||
:4. Crie um código que calcula o valor gasto total (em R$) e o peso total (em kg) da compra de algumas unidades de arroz (5 kg), feijão (1 kg) e café (500 g). | |||
::* O usuário deve fornecer quantas unidades quer comprar de cada produto (comando ''input''). | ::* O usuário deve fornecer quantas unidades quer comprar de cada produto (comando ''input''). | ||
::* Os dados devem ser validados: verificar se o usuário forneceu alguma quantidade negativa. | ::* Os dados devem ser validados: verificar se o usuário forneceu alguma quantidade negativa. | ||
| Linha 709: | Linha 774: | ||
:::# O preço unitário do café é R$10,00. Se comprar 3 ou mais, o preço cai para R$9,25 cada. | :::# O preço unitário do café é R$10,00. Se comprar 3 ou mais, o preço cai para R$9,25 cada. | ||
: | :5. Implemente uma calculadora com as quatro operações básicas, recebendo a escolha de operação e números com o comando ''input''. Não se esqueça de implementar proteções para as entradas de dados (divisão por zero, vetores, etc). | ||
:6. Modifique o programa do cálculo do IMC (Aula 6) de modo a informar ao usuário o grau de magreza/obesidade do indivíduo (veja [https://pt.wikipedia.org/wiki/%C3%8Dndice_de_massa_corporal#Classifica%C3%A7%C3%A3o aqui]). | |||
* A sentença ''switch'' | * A sentença ''switch'' | ||
| Linha 727: | Linha 786: | ||
* '''Exercício''': | * '''Exercício''': | ||
:1. Reescreva o código da | :1. Reescreva o código da questão 2 anterior (bate-papo da UOL) fazendo o uso da sentença ''switch''. | ||
:2. Reescreva o código da questão 5 anterior (calculadora) fazendo o uso da sentença ''switch''. | |||
* [[FIC_MATLAB_2018-2/Aula-9|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 10 - Structs === | |||
{{collapse top| bg=lightblue | 11/Out}} | |||
* Estruturas | * Estruturas | ||
:* Criando estruturas com o comando ''struct'' | |||
:* Criando estruturas com o operador "." | :* Criando estruturas com o operador "." | ||
:* Comando ''isfield'' para identificar se um campo existe ou não | :* Comando ''isfield'' para identificar se um campo existe ou não | ||
:* Comando ''rmfield'' para remover campo da estrutura | :* Comando ''rmfield'' para remover campo da estrutura | ||
* Arranjo de estruturas | |||
* '''Exercícios:''' | * '''Exercícios:''' | ||
:1. Crie um arranjo de estruturas que contenha os os seguintes campos de informação concernentes a pontes rodoviárias em uma cidade: localização da ponte, carga máxima (toneladas), ano de construção, ano agendado para a manutenção. | :1. Crie um programa que utiliza duas estruturas: '''ponto''' e '''reta'''. | ||
::* A estrutura '''ponto''' deve ter como campos as coordenadas do ponto. | |||
::* A estrutura '''reta''' tem como campos os coeficientes angular e linear da reta. | |||
:: O seu programa deve requisitar do usuário as coordenadas do ponto e os coeficientes da reta. Como saída, seu programa deve | |||
::a) Plotar na tela (''plot'') uma figura contendo o ponto e a reta. | |||
::b) Imprimir na tela (''disp'') distância do ponto até a origem. | |||
::c) Imprimir na tela (''disp'') se o ponto pertence à reta. | |||
:: Para testar seu programa: o ponto (3, 4) dista da origem de 5 unidades e pertence à reta ''y = 2x - 2''. | |||
:2. Crie uma estrutura que contenha todas as informações necessárias para construir um diagrama de um conjunto de dados. No mínimo, a estrutura deve conter os seguintes campos: | |||
::* '''x_data''': dado referente ao eixo "x" | |||
::* '''y_data''': dado referente ao eixo "y" | |||
::* '''title''': título do diagrama | |||
::* '''x_label''': rótulo do eixo "x" | |||
::* '''y_label''': rótulo do eixo "y" | |||
::* '''x_range''': faixa de valores exibidos no eixo "x" | |||
::* '''y_range''': faixa de valores exibidos no eixo "y" | |||
:: Você pode adicionar outros campos que aumentem seu controle sobre o diagrama final. | |||
:: Depois de criar essa estrutura, escreva um programa no MATLAB que use a estrutura para gerar um gráfico. O programa deve aplicar características iniciais inteligentes se alguns campos de dados estiverem faltando. | |||
:3. Crie um arranjo de estruturas que contenha os os seguintes campos de informação concernentes a pontes rodoviárias em uma cidade: localização da ponte, carga máxima (toneladas), ano de construção, ano agendado para a manutenção. | |||
::a) Insira os dados abaixo na estrutura: | ::a) Insira os dados abaixo na estrutura: | ||
| Linha 773: | Linha 867: | ||
::c) Adicione a seguinte ponte ao arranjo de estruturas: | ::c) Adicione a seguinte ponte ao arranjo de estruturas: | ||
:::{| class="wikitable" | :::{| class="wikitable" | ||
| Linha 787: | Linha 880: | ||
|} | |} | ||
* [[FIC_MATLAB_2018-2/Aula-10|Códigos executados em sala]] | |||
{{collapse bottom}} | |||
=== 11 - Cells === | |||
{{collapse top| bg=lightblue | 16/Out}} | |||
* Arranjo de células: texto e números | * Arranjo de células: texto e números | ||
| Linha 808: | Linha 895: | ||
* '''Exercícios''': | * '''Exercícios''': | ||
:1. Repita os exercícios | :1. Repita os exercícios da Aula 10 usando células | ||
* [[FIC_MATLAB_2018-2/Aula- | * [[FIC_MATLAB_2018-2/Aula-11|Códigos executados em sala]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Estruturas de repetição - ''for'' e ''while'' === | === 12 - Estruturas de repetição - ''for'' e ''while'' === | ||
{{collapse top| bg=lightblue | | |||
{{collapse top| bg=lightblue | 18/Out}} | |||
* Estruturas de repetição: | * Estruturas de repetição: | ||
| Linha 826: | Linha 915: | ||
* '''Exercícios:''' | * '''Exercícios:''' | ||
:1. Acrescente à calculadora a possibilidade de continuar realizando cálculos até que o usuário solicite a saída digitando 's'. | :1. Acrescente à calculadora (Aula 9) a possibilidade de continuar realizando cálculos até que o usuário solicite a saída digitando 's'. | ||
:2. Escreva um programa que calcule o fatorial de um número, utilizando ''for'' e ''while''. | :2. Escreva um programa que calcule o fatorial de um número, utilizando ''for'' e ''while''. | ||
| Linha 881: | Linha 970: | ||
::Plote em um mesmo gráfico a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando um número de termos definido pelo usuário. | ::Plote em um mesmo gráfico a função ''f''(''x'') e sua representação em série ''g''(''x''), utilizando um número de termos definido pelo usuário. | ||
* [[FIC_MATLAB_2018-2/Aula- | |||
* [[FIC_MATLAB_2018-2/Aula-12|Códigos executados em sala]] | |||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Funções | === 13 - Funções === | ||
{{collapse top| bg=lightblue | | |||
{{collapse top| bg=lightblue | 23/Out}} | |||
* Funções definidas pelo usuário | * Funções definidas pelo usuário | ||
| Linha 896: | Linha 987: | ||
*'''Exercícios:''' | *'''Exercícios:''' | ||
:1. | :1. Escreva as seguintes funções: | ||
::a) Uma função que retorna a média aritmética e a média geométrica de dois dados números. | |||
::b) Modifique o programa do IMC (Aula 9) para que ele seja calculado a partir da chamada de uma função. | |||
::c) Uma função que retira um caracter (passado no primeiro argumento da função) de uma string (passada no segundo argumento da função) | |||
:2. Escreva uma função que | :2. Escreva uma função que determina o tempo (em anos) necessário para que você acumule pelo menos VF (em dólares) em uma conta bancária se você depositar inicialmente V0 (em dólares) e mais P (em dólares) ao final de cada ano, com um rendimento anual de R%. | ||
:3. Escreva | :3. Escreva as seguintes funções: | ||
::a) Uma função que calcule o fatorial de um número; | |||
::b) Uma função que calcule os n primeiros termos da sequência de Fibonacci, dispondo-os num vetor; | |||
::c) Inclua proteções para usuário (para o caso em que o usuário tenha passado algo diferente do esperado como argumento) nas duas funções anteriores. | |||
:4 | :4. Escreva uma função que implementa a [https://pt.wikipedia.org/wiki/Cifra_de_C%C3%A9sar Cifra de César]. A entrada da função deve ser: | ||
::* O ''string'' a ser codificado/decodificado; | ::* O ''string'' a ser codificado/decodificado; | ||
::* O deslocamento a ser aplicado em cada letra do ''string'', podendo ser um inteiro positivo (deslocamento para a direita) ou negativo (deslocamento para a esquerda). | ::* O deslocamento a ser aplicado em cada letra do ''string'', podendo ser um inteiro positivo (deslocamento para a direita) ou negativo (deslocamento para a esquerda). | ||
: | :5. Escreva uma função que retorna todos os números primos menores ou iguais a um dado inteiro ''n''. Utilize o algoritmo do [https://pt.wikipedia.org/wiki/Crivo_de_Erat%C3%B3stenes Crivo de Eratóstenes]. | ||
* | * [[FIC_MATLAB_2018-2/Aula-13|Códigos executados em sala]] | ||
{{collapse bottom}} | |||
=== 14 - Processamento de imagens === | |||
{{collapse top| bg=lightblue | 25/Out}} | |||
: | <!--'''Pro futuro:''' Usar ''im2double''!--> | ||
[[Curso Matlab aplicado ao processamento de imagens - Aula 3]] | |||
* [[FIC_MATLAB_2018-2/Aula-13|Códigos executados na aula]] | |||
* [[FIC_MATLAB_2018-2/Aula- | |||
{{collapse bottom}} | {{collapse bottom}} | ||
=== | === 15 - Importação de dados; Gráficos em 2D e 3D === | ||
{{collapse top| bg=lightblue | 30/Out}} | |||
* Importação de dados | |||
:* Comando ''uiimport'' | |||
:* Formato do separador decimal (''.'' ou '','') | |||
[ | : Exemplo: usar [https://wiki.sj.ifsc.edu.br/images/8/84/Celular4g.txt Celular4g.txt], importar e trabalhar com as funções de matrizes. | ||
*'''Exercícios''': | |||
:1. Com o arquivo [https://wiki.sj.ifsc.edu.br/images/f/fe/Add_user.txt Add_user.txt] (Adições Líquidas de Aparelhos 4G das Operadoras no período), calcular a soma dos anos 2014, 2015 e 2016 (até o momento) por operadora e a soma e a média por período. | |||
* '''Gráficos em 2D''' | * '''Gráficos em 2D''' | ||
| Linha 1 044: | Linha 1 123: | ||
:3. As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. | :3. As seguintes funções descrevem as oscilações em circuitos elétricos e as vibrações de máquinas e estruturas. Sobreponha as plotagens dessas funções no mesmo eixo. Como elas são similares, defina qual é a melhor forma de plotá-las e de rotulá-las para evitar confusão. | ||
::: <math>x(t) = 1000 e^{-0,5t} \mathrm{sen}(3t+2)</math> | ::: <math>\displaystyle{x(t) = 1000 e^{-0,5t} \mathrm{sen}(3t+2)}</math> | ||
::: <math>y(t) = 7 e^{-0,4t} \cos(5t-3)</math> | ::: <math>\displaystyle{y(t) = 7 e^{-0,4t} \cos(5t-3)}</math> | ||
| Linha 1 080: | Linha 1 159: | ||
[[Arquivo:FIC_Matlab_Exercicios_plot.pdf|Exercícios]] | [[Arquivo:FIC_Matlab_Exercicios_plot.pdf|Exercícios]] | ||
* [[FIC_MATLAB_2018-2/Aula- | * [[FIC_MATLAB_2018-2/Aula-14|Códigos executados em sala]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Toolbox simbólico === | === 16 - Solução de sistemas de equações; Toolbox simbólico === | ||
{{collapse top| bg=lightblue | | |||
{{collapse top| bg=lightblue | 01/Nov}} | |||
* Sistemas de equações lineares | |||
:* Encontrando a solução de ''Ax = b'' com ''A\b'' | |||
<!-- Talvez falar sobre a função rref - forma escalonada reduzida de linha --> | |||
::* Exemplo: Balanceamento de equações químicas | |||
:::::<math>C_3 H_8 + O_2 ~~~ \longrightarrow ~~~ CO_2 + H_2 O</math> | |||
:::::<math>x (C_3 H_8) + y (O_2) ~~~ \longrightarrow ~~~ z (C O_2) + w (H_2 O)</math> | |||
:::::<math>\begin{cases} | |||
3x = z & \text{(carbono)} \\ | |||
8x = 2w & \text{(hidrogenio)} \\ | |||
2y = 2z + w & \text{(oxigenio)} \\ | |||
x + y + z + w = 1 & \text{(normalizacao)} \\ | |||
\end{cases}</math> | |||
:::::<math>\begin{cases} | |||
3x - z = 0 \\ | |||
8x - 2w = 0 \\ | |||
2y - 2z - w = 0 \\ | |||
x + y + z + w = 1 \\ | |||
\end{cases}</math> | |||
<!-- [[Image:MATLAB_Chem_Balance.jpg|300px|center]] --> | |||
* Toolbox simbólico | |||
:* Básico | |||
:* | |||
''' | ::* Comandos ''syms'' e ''sym'' | ||
::* Comandos ''pretty'' e ''latex'' | |||
::* Comando ''subs'' | |||
:::* Valores via argumento da função | |||
:::* Valores retirados do workspace | |||
::* Comandos ''factor'', ''expand'', ''collect'' e ''simplify'' | |||
:* Cálculo | |||
:* | |||
* | ::* Comando ''limit'': Limites | ||
:::* <math>\lim_{x \to 0} \frac{\sin(x)}{x}</math> | |||
:::* <math>\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right)^x</math> | |||
::* Comando ''diff'': Derivada primeira, segunda, terceira, etc. | |||
::* Comando ''int'': Integrais indefinidas e definidas | |||
:::* <math>\int x^a dx</math> | |||
* | :* Interlúdio: comandos ''assume'' e ''assumptions'' | ||
* | :* Mais cálculo | ||
''' | ::* Comando ''taylor'': Séries de Taylor | ||
::* Comando ''symsum'': Somatórios / séries | |||
::* Outros: ''dsolve'', ''fourier'', ''laplace'', ''partfrac'' | |||
* Comando ''solve'' | :* Solução de equações | ||
::* Comando ''solve'' | |||
[[FIC_MATLAB_2018-2/Aula- | [[FIC_MATLAB_2018-2/Aula-15|Códigos executados em sala]] | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Interface gráfica === | === 17 - Interface gráfica === | ||
{{collapse top| bg=lightblue | | {{collapse top| bg=lightblue | 06/Nov}} | ||
[[Curso Matlab aplicado ao processamento de imagens - Aula 2|Aula]] | [[Curso Matlab aplicado ao processamento de imagens - Aula 2|Aula]] | ||
| Linha 1 294: | Linha 1 402: | ||
{{collapse bottom}} | {{collapse bottom}} | ||
[[FIC_MATLAB_2018-2/Aula-16|Códigos executados em sala]] | |||
{{collapse bottom}} | {{collapse bottom}} | ||
=== Projeto === | === 18 - Projeto === | ||
{{collapse top| bg=lightblue | 08/Nov}} | |||
{{collapse top| bg=lightblue | | |||
Aula dedicada ao projeto. | Aula dedicada ao projeto. | ||
{{collapse bottom}} | {{collapse bottom}} | ||
=== 19 - Projeto === | |||
{{collapse top| bg= | {{collapse top| bg=lightblue | 13/Nov}} | ||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | {{collapse bottom}} | ||
=== 20 - Projeto === | |||
{{collapse top| bg=lightblue | 20/Nov}} | |||
{{collapse top| bg=lightblue | | |||
Aula dedicada ao projeto. | |||
{{collapse bottom}} | {{collapse bottom}} | ||
Edição atual tal como às 18h10min de 6 de novembro de 2018
1 Informações Básicas
- Código: MLB16470
- Professores: Diego da Silva de Medeiros e Roberto Wanderley da Nóbrega
- Início: 11/Set/2017
- Término: 20/Nov/2017
- Horário: Terças e quintas, das 19h às 22h
- Referência Básica: PALM, William J. Introdução ao MATLAB para engenheiros. Tradução de Tales Argolo Jesus. 3. ed. Porto Alegre: AMGH, 2013. xiv, 562, il. ISBN 9788580552041
- Referência Complementar: MORAIS, V.. VIEIRA, C. MATLAB Curso Completo. FCA, 2013. 644. ISBN 9727227058
2 Conteúdos Abordados
2.1 1 - Apresentação da disciplina; Interface do MATLAB; Operadores; Funções; Constantes especiais; Formatos de exibição
| 11/Set - | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Observações:
|
2.2 2 - Vetores e matrizes
| 13/Set |
|---|
|
|
2.3 3 - Operações com matrizes; Plots
| 18/Set | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.4 4 - Aula de exercícios
2.5 5 - Endereçamento de vetores e matrizes
| 25/Set |
|---|
|
2.6 6 - Concatenação de matrizes; Texto; Entrada e saída de dados; Conjuntos; Polinômios; Números aleatórios
| 27/Set |
|---|
|
2.7 7 - Aula de exercícios
| 02/Out | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.8 8 - Variáveis lógicas; Operadores relacionais e lógicos
| 04/Out | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.9 9 - Controle de fluxo de dados - if e switch
| 09/Out |
|---|
|
2.10 10 - Structs
| 11/Out | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.11 11 - Cells
| 16/Out |
|---|
|
2.12 12 - Estruturas de repetição - for e while
| 18/Out | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.13 13 - Funções
| 23/Out |
|---|
|
2.14 14 - Processamento de imagens
2.15 15 - Importação de dados; Gráficos em 2D e 3D
| 30/Out | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.16 16 - Solução de sistemas de equações; Toolbox simbólico
| 01/Nov |
|---|
|
2.17 17 - Interface gráfica
| 06/Nov | ||
|---|---|---|
|
2.18 18 - Projeto
| 08/Nov |
|---|
|
Aula dedicada ao projeto. |
2.19 19 - Projeto
| 13/Nov |
|---|
|
Aula dedicada ao projeto. |
2.20 20 - Projeto
| 20/Nov |
|---|
|
Aula dedicada ao projeto. |
3 Questões da turma
4 Projetos finais
4.1 Ideias
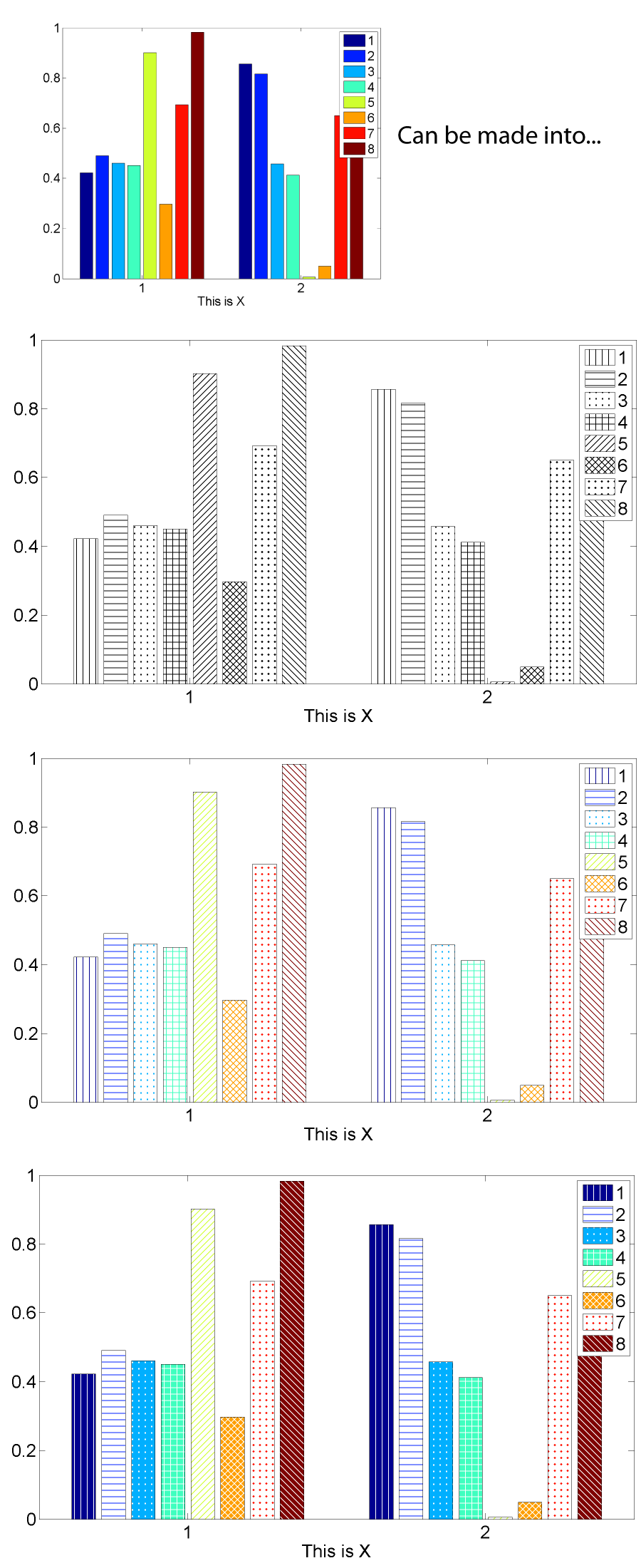
4.1.1 Hachuras em gráficos de barras
Implementar uma função em MATLAB que plote um gráfico de barras com hachuras. O comportamento deve ser semelhante ao comando bar, nativo do MATLAB, mas parâmetros poderão ser acrescentados para controle da trama. Um exemplo de resultado pode ser visto na figura abaixo:
4.1.2 Genius®
Implementar uma versão avançada do jogo Genius® construído na aula 9, adicionando sons, elementos gráficos, etc.
4.1.3 Outros
- relógio analógico
- dtmf
- sudoku
- jogo da velha
- contar moedas
- esteganografia
- batalha naval