CEL18702 2016 2 AULA13: mudanças entre as edições
| (11 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 66: | Linha 66: | ||
[[Imagem:fig106_CEL18702.png|center]] | [[Imagem:fig106_CEL18702.png|center]] | ||
<center> | <center> | ||
Figura 2 - Associação de fontes de tensão. | Figura 2 - Associação em série de fontes de tensão. | ||
</center> | </center> | ||
A associação em paralelo de fontes de tensão é uma operação cuja realização prática necessita de alguns cuidados. Esta recomendação é particularmente verdadeira nos casos em que as fontes de tensão apresentam valores nominais bastante diferenciados e resistências internas reduzidas. Como se ilustra na Figura 3 (a), no caso particular em que as fontes de tensão são ideais e apresentam valores nominais distintos, a sua ligação em paralelo define uma malha cuja solução é apenas compatível com a circulação de uma corrente de valor infinito. Na realidade, a corrente entre as fontes é sempre limitada pelas respectivas resistências internas Figura 3 (b), valor que pode ser bastante elevado se estas não dispuserem de mecanismos de proteção. | |||
[[Imagem:fig107_CEL18702.png|center]] | |||
<center> | |||
Figura 3 - Associação em paralelo de fontes de tensão. | |||
</center> | |||
A associação em paralelo de fontes de tensão é o objeto do Teorema de Millman. De acordo com as regras estabelecidas para a transformação de fonte, o circuito representado na Figura 3 (b) pode ser sucessivamente transformado nos circuitos equivalentes representados em (c) e (d). Na primeira transformação, Figura 3 (c), substitui-se cada uma das fontes de tensão pela respectiva fonte de corrente equivalente, efetuando-se depois, sucessivamente, as associações em paralelo das fontes de corrente e das resistências internas, e a transformação inversa numa fonte de tensão com resistência interna. É facilmente demonstrável que os parâmetros da fonte de tensão resultante são: | |||
<math>V_5=\frac{G_1.V_1+G_2.V2}{G_1+G_2}\,</math> | |||
e | |||
<math>R_5=\frac{R_1.R_2}{R_1+R_2}\,</math> | |||
respectivamente para o valor nominal da tensão e para a resistência interna. | |||
==Fonte de Corrente== | |||
http://www.ufrgs.br/eng04030/Aulas/teoria/cap_04/assocfon.htm | |||
==Exercícios== | ==Exercícios== | ||
| Linha 79: | Linha 104: | ||
<math>V_{AB}=7,5V\,,I=0,125A</math> | <math>V_{AB}=7,5V\,,I=0,125A</math> | ||
{{collapse bottom}} | |||
[2] Calcule V<sub>AB</sub> com o circuito em aberto e depois com R<sub>c</sub>=3Ω ligada ao circuito. | |||
[[Imagem:fig102_CEL18702.png|center|400px]] | |||
{{collapse top|Respostas}} | |||
V<sub>Th</sub>=4,2V; R<sub>Th</sub>=R<sub>N</sub>=3Ω; I<sub>N</sub>=1,4A; V<sub>AB</sub>=2,1V | |||
{{collapse bottom}} | |||
[3] Calcule a tensão sobre o resistor de 4Ω. | |||
[[Imagem:fig109_CEL18702.png|center|400px]] | |||
{{collapse top|Respostas}} | |||
V<sub>4Ω</sub>=6,9V | |||
{{collapse bottom}} | |||
[4] Calcule a tensão sobre o resistor de 6Ω. | |||
[[Imagem:fig108_CEL18702.png|center|400px]] | |||
{{collapse top|Respostas}} | |||
V<sub>6Ω</sub>=-14,8V | |||
{{collapse bottom}} | {{collapse bottom}} | ||
| Linha 85: | Linha 153: | ||
[1] http://www.corradi.junior.nom.br/teoremas_exer_resolvido.pdf | [1] http://www.corradi.junior.nom.br/teoremas_exer_resolvido.pdf | ||
Edição atual tal como às 11h58min de 22 de novembro de 2016
1 Teorema de Millman
O Teorema de Millman apresenta um método usado para reduzir um número qualquer de fontes de tensão em paralelo a apenas uma. Este teorema constitui um caso especial da aplicação do teorema de Thévenin. A seguir, a partir de um exemplo este método é apresentado. A Figura 1 apresenta um exemplo de simplificação utilização o teorema de Millman.
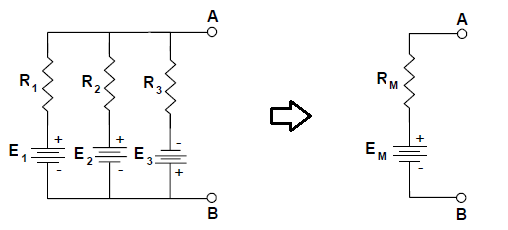
Figura 1 - Teorema de Millman para simplificação de fontes de tensão.
O primeiro passo é transformar as fontes de tensão com resistência em série em fontes de corrente com resistências em paralelo. A seguir, deve-se calcular o circuito equivalente com uma única fonte de corrente e uma única resistência. Estes cálculos são feitos da seguinte maneira:
A transformação do circuito fonte de corrente e resistência em paralelo em fonte de tensão e resistência em série deve ser realizada da seguinte maneira:
1.1 Exemplo
Determinar a corrente na resistência de 5 ohms utilizando o teorema de Millman. Confirme os resultados utilizando o teorema de Thevenin.
| Solução |
|---|
Corrente (I):
Resistência equivalente (R):
Logo:
|
2 Associação de Fontes
2.1 Fontes de Tensão
A associação em série de fontes de tensão permite aumentar a diferença de potencial disponibilizada para efeitos de alimentação de um circuito. Um exemplo da associação em série de fontes é a utilização de múltiplas pilhas para alimentar aparelhos eletrodomésticos como lanternas, rádios portáteis. Com efeito, é comum associarem-se em série quatro pilhas de 1.5 V (corretamente associadas) para definir uma fonte de alimentação de 6 V.
A tensão disponível aos terminais de uma associação em série de fontes de tensão é dada pela soma das tensões parciais. Como se indica nas Figuras 2 (a) e 2 (b), a adição dos valores nominais das tensões deve ter em conta a polaridade da ligação: polaridades concordantes adicionam-se (a), e polaridades discordantes subtraem-se (b). Por outro lado, no caso das fontes de tensão com resistência interna não nula, como na Figura 2 (c), o valor da resistência interna resultante é dado pela soma das resistências internas de cada uma das fontes. A associação em série conduz, por conseguinte, a uma fonte cuja resistência interna é superior àquela característica de cada uma, considerada isoladamente.
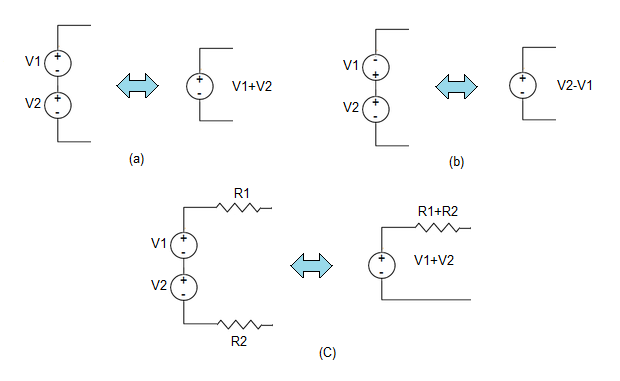
Figura 2 - Associação em série de fontes de tensão.
A associação em paralelo de fontes de tensão é uma operação cuja realização prática necessita de alguns cuidados. Esta recomendação é particularmente verdadeira nos casos em que as fontes de tensão apresentam valores nominais bastante diferenciados e resistências internas reduzidas. Como se ilustra na Figura 3 (a), no caso particular em que as fontes de tensão são ideais e apresentam valores nominais distintos, a sua ligação em paralelo define uma malha cuja solução é apenas compatível com a circulação de uma corrente de valor infinito. Na realidade, a corrente entre as fontes é sempre limitada pelas respectivas resistências internas Figura 3 (b), valor que pode ser bastante elevado se estas não dispuserem de mecanismos de proteção.
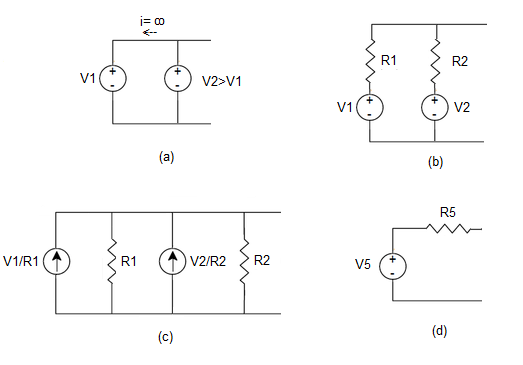
Figura 3 - Associação em paralelo de fontes de tensão.
A associação em paralelo de fontes de tensão é o objeto do Teorema de Millman. De acordo com as regras estabelecidas para a transformação de fonte, o circuito representado na Figura 3 (b) pode ser sucessivamente transformado nos circuitos equivalentes representados em (c) e (d). Na primeira transformação, Figura 3 (c), substitui-se cada uma das fontes de tensão pela respectiva fonte de corrente equivalente, efetuando-se depois, sucessivamente, as associações em paralelo das fontes de corrente e das resistências internas, e a transformação inversa numa fonte de tensão com resistência interna. É facilmente demonstrável que os parâmetros da fonte de tensão resultante são:
e
respectivamente para o valor nominal da tensão e para a resistência interna.
2.2 Fonte de Corrente
http://www.ufrgs.br/eng04030/Aulas/teoria/cap_04/assocfon.htm
2.3 Exercícios
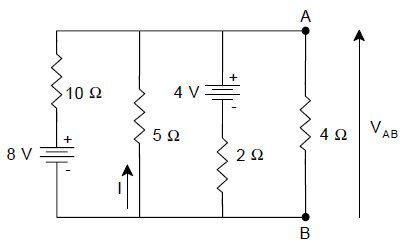
[1] Calcule, utilizando o teorema da superposição, o circuito equivalente ao circuito dado, visto de (A e B). Calcule tensão e corrente em .
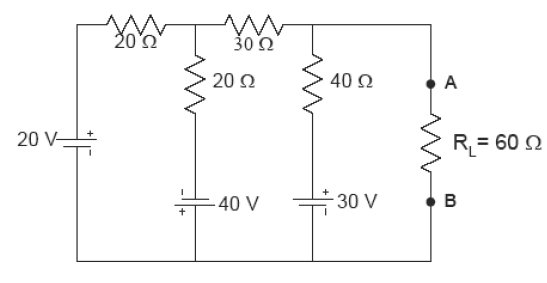
| Solução |
|---|
|
|
[2] Calcule VAB com o circuito em aberto e depois com Rc=3Ω ligada ao circuito.

| Respostas |
|---|
|
VTh=4,2V; RTh=RN=3Ω; IN=1,4A; VAB=2,1V |
[3] Calcule a tensão sobre o resistor de 4Ω.
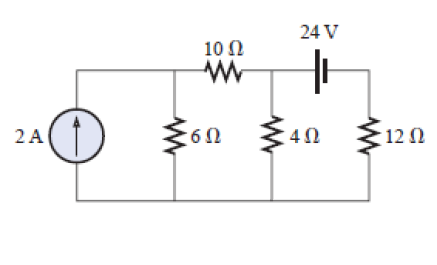
| Respostas |
|---|
|
|
[4] Calcule a tensão sobre o resistor de 6Ω.
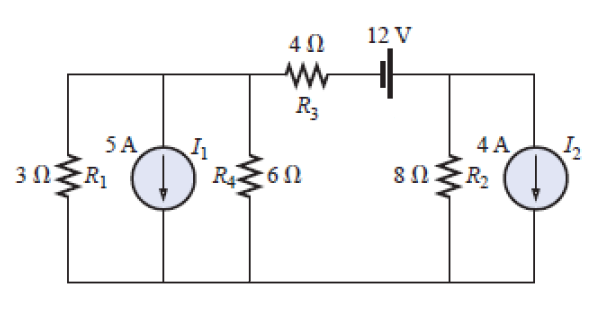
| Respostas |
|---|
|
|
3 Referências
[1] http://www.corradi.junior.nom.br/teoremas_exer_resolvido.pdf
| << | <> | >> |
|---|