Reconhecimento de Placas de Sinalização Via Processamento Digital de Imagem e Aprendizado de Máquina
- Aluno: Mathias Silva da Rosa
- Orientador: Diego da Silva de Medeiros
Monografia
Monografia de TCC - Mathias Silva da Rosa - Engenharia de Telecomunicações
Revisão bibliográfica
| Trabalhos Analisados | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
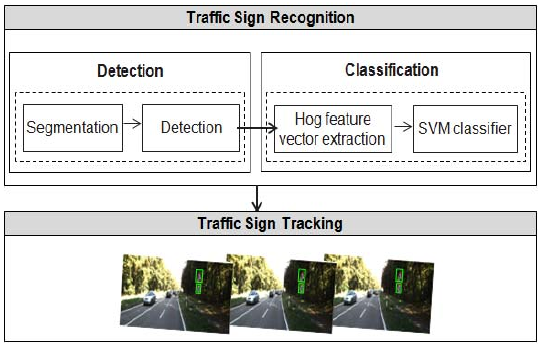
Trabalhos Estrangeiros Romdhane - An improved traffic signs recognition and tracking method for driver assistance system - Usa segmentação via cor e HOG (Histogram of Oriented Gradients) Mammeri - Traffic Signs Localisation and Recognition Using A Client-Server Architecture - Usa um sistema centralizado, semelhante ao GPS
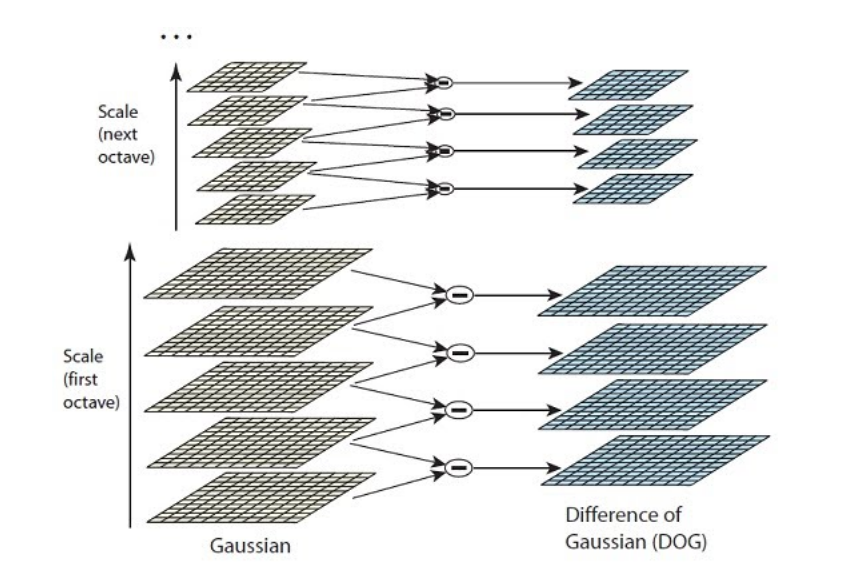
Gao - Traffic signs recognition based on PCA-SIFT - Traz um apanhado geral sobre vários tipos de técnicas. Usa pré-processamento, SIFT (Scale-Invariant Feature Transform e SVM(Support Vector Machine)
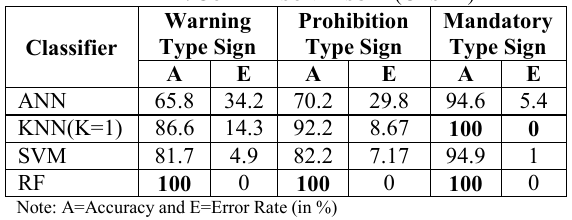
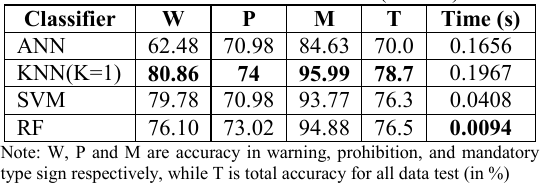
Wahyono - A comparative study of classification methods for traffic signs recognition - Compara diversos métodos: Redes Neurais artificiais (ANN), Vizinhos k-Próximos (kNN), SVM, Random Forest (RF) e HOG (Histogram of Oriented Gradients)
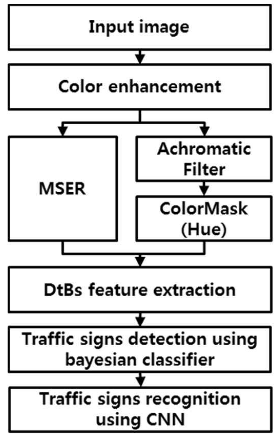
Jang - Data debiased traffic sign recognition using MSERs and CNN - Usa componentes de cor
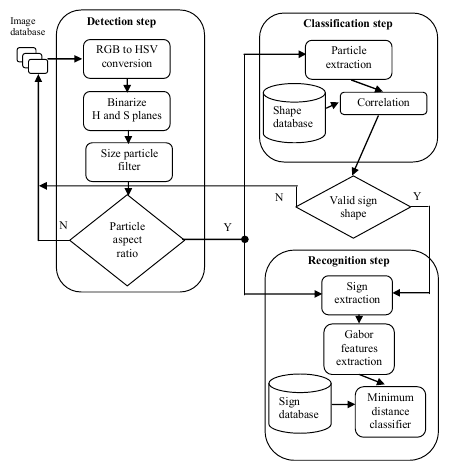
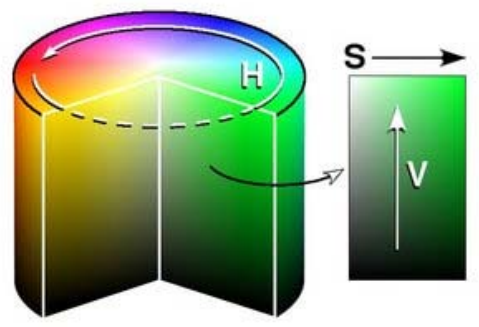
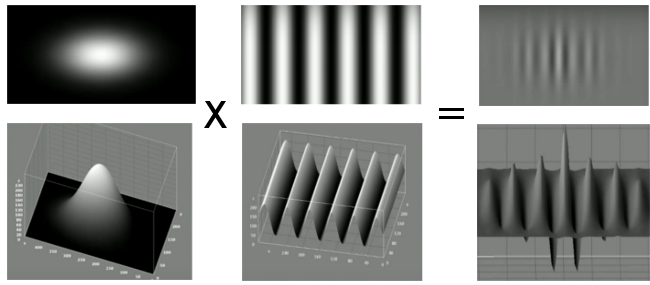
Mariut - Detection and recognition of traffic signs using Gabor filters - Usa espaço de cores HSV (matiz, saturação e valor), classificação por correlação e reconhecimento via distância euclidiana e filtro de Gabor
Chen - A Robust Traffic Sign Recognition System for Intelligent Vehicles - Classificação via Filtro Vetorial Simples, Transformada Hough e Curve Fitting, e classificação via Momentos Pseudo-Zernike
Trabalhos Brasileiros
|
| Trabalhos a serem analisados | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Trabalhos Estrangeiros Romdhane - Combined 2d/3d traffic signs recognition and distance estimation - Usa uma estrutura parecida, porém acrescenta o SVM
Feng - Ground traffic signs recognition based on Zernike moments and SVM - Usa os Momentos de Zernike e SVM
Elotmani - A light traffic signs recognition system - Usa detecção de cores e Projeção de Perfil
Wang - Traffic-signs recognition system based on multi-features - Usa um método de segmentação FCM (Fuzzy c-Means) e classificação CBIR (Content-Based Image Retrieval)
Lin - A Traffic Sign Recognition Method Based on Deep Visual Feature - Filtro Bilateral, Detector de Bordas Canny, Rede Neural Convolucional(CNN) e Máquina de Vetores de Suporte (SVM)
Greenhalgh - Real-Time Detection and Recognition of Road Traffic Signs - Maximally Stable Extremal Regions (MSER), Histograma de Gradientes Orientados (HOG) e Cascata de SVMs.
Trabalhos brasileiros Poffo - Visual Autonomy - Protótipo para reconhecimento de placas de trânsito
Silva - Uma Metodologia para Detectar e Reconhecer Placas de Sinalização de Trânsito
|
Análise dos Trabalhos
| Trabalho | Ano | Extração da Região de Interesse | Descrição | Reconhecimento |
|---|---|---|---|---|
| Gao | 2014 | N/A | Scale-Invariant Feature Transform (SIFT)+ Análise dos Componentes Principais (PCA) | Máquina de Vetores de Suporte(SVM) |
| Wahyono | 2014 | Segmentação das Cores (Binarização de Matiz e Saturação) + Classificação da Forma(Centroid-Based Graph) | Histograma de Gradientes Orientados(HOG) |
Rede Neural Artificial(ANN) K-Vizinhos mais Próximos Máquina de Vetores de Suporte(SVM) Random Forest(RF) |
| Jang | 2016 | Normalização das Cores Vermelhas e Azul + Maximally stable extremal regions (MSER) | Bayesian com vetor Distance to Border(DtB) | Rede Neural Convolucional |
| Mariut | 2011 | Plano HSV + Binarização de Matiz e Saturação + Size Filter | Correlação com Banco de Imagens | Banco de Filtros de Gabor + Banco de Imagens |
| Chen | 2011 | Filtro Simples de Vetores(Segmentação de Cores) |
Transformada de Hough Interpolação Bicúbica Pseudo-Momentos de Zernike | Máquina de Vetores de Suporte(SVM) |
| Lin | 2016 | Filtro Bilateral + Detector de Bordas Canny | Rede Neural Convolucional(CNN) | Máquina de Vetores de Suporte(SVM) |
| Greenhalgh | 2012 | Maximally Stable Extremal Regions (MSER) | Histograma de Gradientes Orientados (HOG) | Cascata de SVMs |
Legenda:
Complexidade Baixa
Complexidade Média
Complexidade Alta
Proposta
| Pré-processamento | Segmentação | Descrição | Classificação |
|---|---|---|---|
| Limiarização através do HSV + Remoção de áreas (Quant. de pixels e centros de massa) + Dilatação e Erosão | Transformada Hough Generarizada | Histrograma de Gradientes Orientados(HOG) | Máquina de Vetores de Suporte(SVM) |
Cronograma
| Atividades | 2017 | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ago | Set | Out | Nov | Dez | ||||||||||||||||
| Estudo e implementação de técnica de descrição | - | - | - | x | x | x | x | |||||||||||||
| Estudo e implementação de técnica de classificação | x | x | x | x | ||||||||||||||||
| Estudo e implementação de técnica de pré-processamento | x | x | x | |||||||||||||||||
| Estudo e implementação de técnica de detecção | x | x | x | |||||||||||||||||
| Estudo e implementação de técnica de segmentação | x | x | ||||||||||||||||||
| Validação do Sistema | x | |||||||||||||||||||
| Apresentação e Discussão dos Dados | x | |||||||||||||||||||
| Conclusão | x | |||||||||||||||||||
| Escrita da Monografia | x | x | x | x | ||||||||||||||||
| Entrega do TCC | x | |||||||||||||||||||
Estudo das Técnicas
Histograma de Gradientes Orientados (HOG)
Gradientes
| Conteúdo |
|---|
|
Na área da visão computacional, uma imagem digital é considerada como uma representação discreta dos dados presentes nessa imagem, formada pela relação entre o valor espacial (posição) dos dados e a informação de cor que esses dados possuem [4][nota 1], como descrito anteriormente no tópico 2.1 Processamento Digital de Imagens. As informações de cor de uma imagem digital são definidas através de um ou mais canais de intensidade ou cor em uma particular posição da imagem. Uma imagem digital contém um ou mais canais que são definidos através da A luz sem cor, chamada de luz monocromática, possui como um de seus mais importantes atributos a intensidade. Pelo fato de a intensidade ser percebida como variações de preto a tons de cinza até chegar ao branco, o termo níveis de cinza geralmente é utilizado para denotar a intensidade monocromática de uma imagem. Em termos de hardware, a intensidade quantificada resulta na resolução de intensidade, onde os níveis de intensidade são definidos por , sendo k um número inteiro. O número mais comum é 8 bits, resultando em um escala de 256 níveis de intensidade[5]. Em uma imagem digital, a resolução de intensidade está bastante relacionada com a resolução espacial, em outras palavras, para cada pixel de uma imagem e definido um nível de intensidade e para este processo é dado o nome de quantização. O processo de quantização nada mais é do que converter dados de uma imagem em elementos discreto e permite que uma imagem possa ser processada computacionalmente. A intensidade ou os níveis de cinza, são comumente representados através de gradientes. Em um ponto de uma imagem f, o gradiente é definido como um vetor: 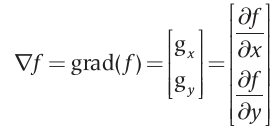 Este vetor gradiente tem a importante propriedade geométrica de apontar no sentido de maior taxa de variação de no ponho . A magnitude do vetor determina o valor da taxa de variação na direção do vetor gradiente e é definida por: Onde e são imagens do mesmo tamanho que a imagem original, criadas quando e podem variar ao longo de todas as posições de pixels em . A direção do vetor gradiente, assim como as demais propriedades citadss, também é uma imagem de mesmo tamanho que a original criada pela divisão de pela imagem . O ângulo do vetor é definido como: 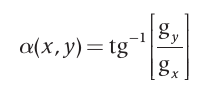 Em nosso trabalho, os gradientes podem ser extraídos através dos histogramas das imagens, como serão descritos no próximo tópico. |
Histograma
| Conteúdo |
|---|
|
O histograma é uma das formas mais comuns de se representar uma distribuição de intensidade de uma imagem, e possivelmente a mais útil no processamento digital de imagens. Um histograma de uma imagem nada mais é que um conjunto de números que indica o percentual de pixels que representam um determinado nível de cinza. Estes valores são normalmente representados por um gráfico de barras que fornece para cada nível de cinza o número de pixels correspondentes na imagem[6]. Um histograma de uma imagem digital com L possíveis níveis de intensidade dentro de uma faixa é uma função discreta definida por: Onde é k-nésimo pixel na imagem, do qual possui intensidade [7]. Geralmente, utiliza-se um histograma normalizado, obtido simplesmente dividindo todos os elementos de pelo número total de pixels na imagem, denotado por: Da estatística básica, considera-se como um estimativa da probabilidade da ocorrência do nível de intensidade , ou seja, um histograma nada mais é que uma função de distribuição de probabilidades de intensidades e como tal deve obedecer aos axiomas e teoremas da teoria da probabilidade[6]. Para exemplificar, a figura 1 abaixo apresenta o histograma de uma imagem clara. 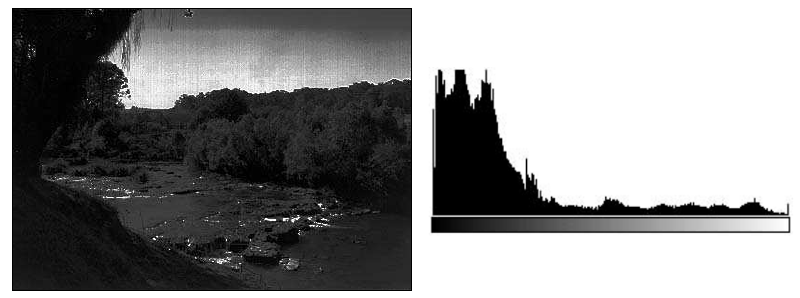 |
Representação e Descritores de Imagem
| Conteúdo |
|---|
|
Após a segmentação da região de interesse na imagem, é necessário que esta região seja representada adequadamente para o futuro processamento computacional. Esta representação envolve utilizar características externas (bordas) e internas (pixels) da região e descrevê-la com base em fatores diretamente relacionados à representação escolhida[5]. No caso das bordas, por exemplo, pode-se calcular a distância entre duas bordas adjacentes para determinar o tamanho da região de interesse. A decisão de qual representação utilizar está relacionada às características da região das quais serão utilizadas para o processamento computacional. Uma representação externa é escolhido quando o foco principal é o formato, enquanto que uma representação interna é escolhida quando o foco principal são cores e texturas[5]. Os descritores são formas de converter características relacionadas às representações. Proporcionalmente, existem dois tipos de descritores: para características externas e características internas. Para as bordas de uma região de interesse, um descritor seria seu comprimento, do qual é aproximado pelos pixels ao longo da fronteira [5]. Descritores Topológicos Os descritores topológicos são descritores que representam adequadamente uma características de imagem e não são afetados por transformações na imagem. Por exemplo, se um descritor topológico é definido como o número de buracos na imagem, esta propriedade, obviamente, não será afetada por transformações de alongamento ou de rotação na imagem. |
Histrograma de Gradientes Orientados - HOG
| Conteúdo |
|---|
|
A ideia inicial do conceito de Histograma de Gradientes Orientados(HOG) relaciona-se ao fato de que características como aparência e forma de objetos em uma imagem pode ser descritos através da distribuição de gradientes de intensidade dos pixels. Para descrever uma região através de um HOG são necessárias cinco etapas:(A) computação do gradiente de cada pixel, (B) divisão da imagem em células, (C) obtenção do histograma 1-D da célula, (D) normalização através de blocos e (E) obtenção do descritor. Computação dos gradientes de cada pixels: Existem várias formas de computar os gradientes de cada pixel em uma imagem, porém a forma mais utilizada é aplicando máscaras |
Máquina de Vetores de Suporte (SVM)
Máquina de Vetores de Suporte (do inglês, Support Vector Machinev - SVM) é um método de aprendizado de máquina supervisionado para reconhecimento binário de padrões baseado na teoria de aprendizado estatístico criada por (Vapnik, 1998) e colaboradores. As SVM's se tornaram famosas nas últimas décadas por possuírem performance comparável e muitas vezes superior às obtidas por outros algoritmos de aprendizado, como as Redes Neurais Artificiais (RNA's)[8][nota 1].
Alguns dos motivos para isso estão fundamentados no bom desempenho desta técnica na generalização de bases de reais, nos recursos teóricos bastante consolidados, no processo de treinamento que elimina a possibilidade de mínimos locais e na existência de poucos parâmetros livres para ajustá-lo. Por isso, esta técnica vem sendo empregada em diversas áreas como categorização de texto, reconhecimento de escrita e voz, classificação de imagens, análise de biosequências, etc [9][nota 2].
Para descrever esta técnicas é essencial detalhar conceitos como aprendizado de máquina, teoria do aprendizado estatístico, vetores, etc. O próximo tópico tratará do aprendizado de máquina com o objetivo introduzir a base do desenvolvimento das SVM's.
Aprendizado de Máquina
| Conteúdo |
|---|
|
Basicamente, o aprendizado de máquina busca extrair conhecimento através de dados. Também denominada como análise preditiva ou aprendizado estatístico, este campo de conhecimento converge de uma intersecção entre estatística, inteligência artificial e ciência da computação[10][nota 1]. Por meio da concepção de técnicas que desenvolvem o aprendizado a partir de sistemas computacionais capazes de adquirir conhecimento de forma automática, o aprendizado de máquina proporciona o nascimento de diversas aplicações em diversas áreas, como no campo da visão, reconhecimento de voz, robótica, medicina, telecomunicações, etc [11][nota 3]. Na sua essência, o aprendizado de máquina se baseia principalmente no conceito de indução, em outras palavras, a inferência lógica que permite obter conclusões genéricas sobre um conjunto particular de exemplos. É através da indução que o cérebro humano pode derivar conhecimento novo sobre situações anteriormente apresentadas. Para isso é necessário que se tenha um conjunto de exemplos de treinamento do qual deverá se entrada do algoritmo de aprendizado [12][nota 4]. Entretanto, muitas vezes as hipóteses levantadas através da indução não necessariamente podem preservar a verdade. Um conjunto de exemplos insuficientes ou exemplos que não foram bem escolhidos podem formar hipóteses inválidas, influenciando na eficácia do sistema. Neste contexto, compreender o poder e a limitação de cada algoritmo utilizando uma metodologia que permite avaliar os conceitos induzidos por esses algoritmos em determinadas situações, é a principal atividade a ser realizada antes do desenvolvimento do sistema em si[12][nota 4]. O aprendizado indutivo pode ser dividido em supervisionado e não supervisionado dependendo do modo em que é obtido o conhecimento. Aprendizado Supervisionado No Aprendizado Supervisionado é fornecido ao algoritmo um conjunto de exemplos de treinamento para os quais os atributos que descrevem alguma característica ou aspecto são conhecidos. Um exemplo nada mais é do que um tupla de atributos passado ao algoritmo com o objetivo de construir um bom classificador que possa determinar corretamente a classe dos novos exemplos que ainda não foram rotulados, ou seja, exemplos dos quais os atributos são desconhecidos [13][nota 5]. Após a concepção do classificador, é possível avaliá-lo em relação ao seu grau de precisão, velocidade de aprendizado, compreensibilidade ou qualquer outro parâmetro que defina a qualidade deste classificador mediante a tarefa em questão [12][nota 6]. Um dos principais fatores limitantes da qualidade de um classificador é a sua capacidade de trabalhar com dados imperfeitos, ou o denominado ruído. O ruído pode ser derivado do próprio processo que gerou os dados, do processo de aquisição, classes rotuladas incorretamente, etc [11][nota 7]. No aprendizado supervisionado, podemos ainda categorizá-lo em classificação e regressão. A classificação tem como objetivo determinar a classe em que um exemplo de entrada pertence. Para isso, o modelo analisa os outros exemplos fornecidos anteriormente e que já possuem indicação de classe, a fim de aprender como classificar o novo registro. Já a regressão é utilizada quando um exemplo é identificado por um valor numérico e não um valor categórico. Assim, pode-se determinar o valor de uma determinada variável analisando-se os valores das demais[14][nota 8]. Aprendizado Não-supervisionado No aprendizado não-supervisionado, o indutor analisa os exemplos fornecidos e tenta determinar se alguns deles podem ser agrupados de alguma maneira, formando agrupamentos ou os denominados clusters. Apos a determinação dos agrupamentos, normalmente, é necessária uma análise para determinar o que cada agrupamento significa no contexto do problema que está sendo analisado [11][nota 9]. A figura abaixo apresenta a hierarquia completa do aprendizado de máquina: 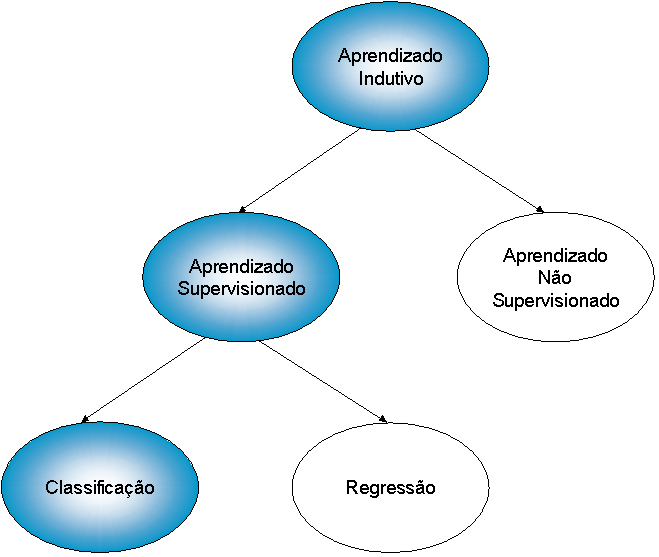 Paradigma de Aprendizado Existem diversos paradigmas de aprendizado que estabelecem a forma em que o conhecimento é adquirido por um sistema baseado em aprendizado de máquina. Entre os paradigmas estão o simbólico, o baseado em eventos, o conexionista, o genético e o estatístico [12][nota 10]. No nosso contexto, vamos focar apenas no paradigma de aprendizado estatístico do qual foi a base para o desenvolvimento das SVM's. |
Teoria do Aprendizado Estatístico
| Conteúdo |
|---|
|
Um mesmo algoritmo de aprendizado, pode ser treinado utilizando diferentes parâmetros e diferentes conjuntos de treinamento, consequentemente, este mesmo algoritmo pode conceber diferentes classificadores para um mesmo cenário. O problema de selecionar o classificador dentro do conjunto de classificadores gerados pelo algoritmo é denominado seleção de modelo e a solução para este problema é a determinação de performance destes classificadores através da Teoria do Aprendizado Estatístico [13][nota 11]. Considere um conjunto treinamento composto por duas classes representadas por círculos e triângulos, onde os elementos de cada classes são definidos através de tuplas de exemplos (). Através do processo de aprendizagem um algoritmo fornece 3 classificadores , e pertencentes ao conjunto de todos o possíveis classificadores gerados por estes mesmo algoritmo. Este cenário é apresentado pela figura abaixo [11][nota 12]. 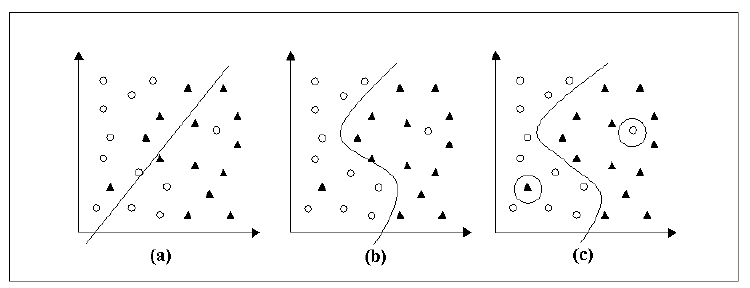 O classificador utilizada uma fronteira de decisão linear sobre o conjunto onde os pontos extremos das duas classes são muito próximos entre si, por isso são considerados não confiáveis [8][nota 13]. Neste caso, o classificador comete muitos erros, mesmo para casos muito simples. Pode-se considerar que houve um subajuste do classificador, uma vez que este não é capaz de se ajustar às instâncias de treinamento[9][nota 14]. Em contra partida, o classificador utiliza fronteiras de decisão complexas e difíceis de serem definidas matematicamente, possuindo a capacidade alta de determinar exemplos do conjunto de treinamento, mas com grandes possibilidades de cometer erros quando confrontado com novos exemplos. Pode-se considerar que houve um sobreajuste, onde considera-se que o classificador memorizou os dados do conjunto de treinamento [8][nota 15]. O classificador seria considerado um intermediário entre as duas propostas anteriormente mencionadas. Nesta hipótese, o classificador utiliza uma fronteira não linear com baixa complexidade de definição e por isso consegue determinar com sucesso quase todas as classes do conjunto de treinamento[8][nota 15]. Sendo assim, o problema da seleção de modelo é resolvido quando o melhor desempenho de generalização é atingindo através do equilibro entre a precisão alcançada em um conjunto de treinamento particular e capacidade do sistema de aprender qualquer conjunto de treinamento sem erro [9][nota 14]. Para isso, busca-se a aproximação entre uma determinada função alvo e a saída real do sistema. A entre as duas funções pode ser mensurada através da estimação do erro mínimo (também denominado risco mínimo), do qual mede a capacidade de generalização de [15][nota 16]. Assumindo-se que os exemplos apresentados pelo conjunto de treinamento são independentes e identicamente distribuídos de acordo com uma distribuição de probabilidade , o erro esperado é definido por: Onde, é uma função de custo relacionando a previsão quando a saída desejada é [8][nota 15]. No caso de uma classificação binária, uma função comumente usada é a , que retorna o valor 0 se é classificado corretamente e 1 caso contrário.</math>.Entretanto, a minimização do risco esperado não pode ser realizada diretamente com esta equação, uma vez que em geral a distribuição de probabilidade é desconhecida. No processo de aprendizagem, a única informação disponível está contida no conjunto de treinamento que também é amostrado de [15][nota 17]. Para contornar esta dificuldade matemática, é utilizado o princípio indutivo da minimização do risco empírico. O risco empírico, apresentado pela equação abaixo, mede o desempenho do classificador nos dados de treinamento, por meio da taxa de classificações incorretas obtidas no conjunto de treinamento [8][nota 18]. Nesta equação, Com , é possível estabelecer um critério de aceitação para qual a performance do classificador em questão é apropriada para o problema de classificação especifico, ou seja,é possível obter classificadores cujo valores de risco empírico convergem para o risco esperado [9][nota 19]. Entretanto, para conjunto de treinamento menores, geralmente não é possível determinar esse tipo de garantia. Neste contexto, dentro de um conjunto amplo de classificadores é sempre possível encontrar um classificador com risco empírico pequeno [8][nota 18]. Deve-se então restringir os classificadores através de limites dos risco esperado e com isso a Teoria do Aprendizado Estatístico fornece ferramentas para mensurar a capacidade de cada classificador. A ferramenta mais utilizada é a Dimensão VC, que é componente importante para o limite de generalização da SVM [9][nota 20]. A dimensão VC (Vapnik-Chervonenkis) é uma medida de capacidade de classificação sobre a família de funções geradas por um algoritmo de aprendizado, em outra palavras, é o valor que representa o número de exemplos necessários para se aprender um classe de interesse de maneira confiável [15][nota 21]. Quando maior for a dimensão VC, maior será o número de exemplos necessários para aprender a classe. O erro de generalização, diferentemente do erro de treinamento (risco empírico), é a taxa de erros de um determinado classificador aplicado à um conjunto de exemplos que ainda não foram vistos. Para calcular a capacidade de generalização, é necessário mensurar o limitante da respectiva taxa de erro através da soma dos dois elementos anteriormente mencionados: o risco empírico e a dimensão VC [9][nota 22]. As máquinas de aprendizado que buscam minimizar o limitante superior são ditas seguir o princípio estatístico da minimização de risco estrutura. Entre estas máquinas está a Máquina de Vetores de Suporte (do inglês, Support Vector Machine - SVM) que objetivam aumentar a capacidade de generalização através da minimização do risco empírico e da dimensão VC [8][nota 23]. |
Support Vector Machine - SVM
| Conteúdo |
|---|
|
SVM Lineares Na sua forma mais simples, o objetivo de uma SVM é a obtenção de fronteiras lineares para separação dos dados em duas classes (classificação binária). A classificação linear consegue apenas delimitar classes que pertencem à um conjunto linearmente separável, enquanto que a classificação não-linear consegue delimitar classes que pertencem à um conjunto não-linearmente separável [8][nota 23]. Sendo assim, são poucas as aplicações que podem utilizar a classificação linear, uma vez que aplicações reais necessitam de fronteiras de complexa definição aumentando consequentemente a complexidade do sistema classificador [9][nota 24]. Apesar de sua limitação, a classificação linear apresenta propriedades importantes para o embasamento inicial da SVM's. No caso da minimização do risco estrutural, uma SVM Linear produz um valor zero para o primeiro termo e minimiza o segundo termo para definir os limites [15][nota 25]. A figura abaixo apresenta apresenta em (a) um conjunto de treinamento linearmente separável em um espaço bidimensional, enquanto que (b) apresenta um conjunto não-linearmente separável. A linha apresentada em ambas as situações são denominada de superfície de decisão. No caso da (a), devido a linearidade da superfície de decisão, esta também é denominada de hiperplano [8][nota 23]. 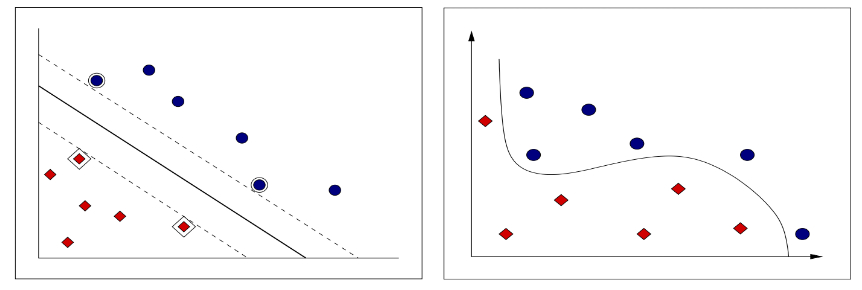 No contexto de aprendizado de máquina, um hiperplano é um espaço de separação n dimensional. Em um espaço bidimensional, um hiperplano é definido através de um reta, enquanto em um espaço tridimensional, um hiperplano é definido através de um plano [16][nota 26]. O algotirmo de um SVM tem como principal objetivo encontrar um hiperplano de margem máxima, do qual separa corretamente todas as classes de um determinado conjunto e mantém a maior distância entre os vetores mais próximos à este hiperplano [9][nota 27]. O hiperplano que que detém destas características é denominado hiperplano ótimo e os vetores que mais se aproximam deste hiperplano são denominados de vetores de suporte [15][nota 28]. Para a definição de um hiperplano aplicado à classificação linear, utiliza-se a equação da reta no formato como é apresentado abaixo:
Essa equação segmenta o conjunto de dados em duas regiões: e . Seja um ponto no hiperplano de forma que e um ponto no hiperplano de forma que , conforme a figura abaixo, é possível estabelecer a distância através dos vetores normais perpendiculares ao hiperplano direcionados aos respectivos pontos, conforme imagem abaixo. 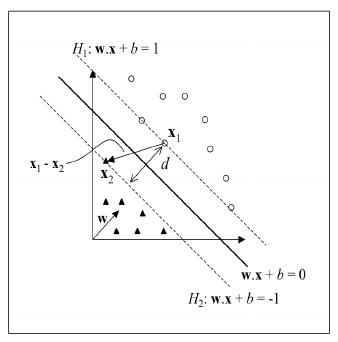 O comprimento do vetor projetado através da diferenças entre os vetores normais é dados por , onde é possível obter a maximização da margem entre o hiperplano e os vetores de suporte através da minimização de . SVM's Lineares com Margens Suaves Em aplicações reais, raramente o conjunto de dados é linearmente separável. Isso se deve a diversos fatores como presença de ruídos, outliers (exemplos fora da curva) ou à própria natureza do problema. Para tentar contornar esta dificuldade, a SVM's lineares são estendidas para lidar com conjuntos de treinamento mais gerais. Para realizar essa tarefa é necessário que alguns dados possam violar a restrição imposta anteriormente ( e ). Este procedimento suaviza as margens da fronteira de classificação, permitindo que alguns dados permaneçam dentro da margem máxima e também a ocorrência de alguns erros de classificação. O critério de quantas classificações podem ser realizadas de forma errônea é definido através do risco empírico. SVM's com estas características são denominas SVM lineares com margens suaves. SVM's Não Lineares Há casos de conjuntos de dados dos quais não são possíveis de serem separados através de um hiperplano. Exemplos disso são apresentados através da figura abaixo. 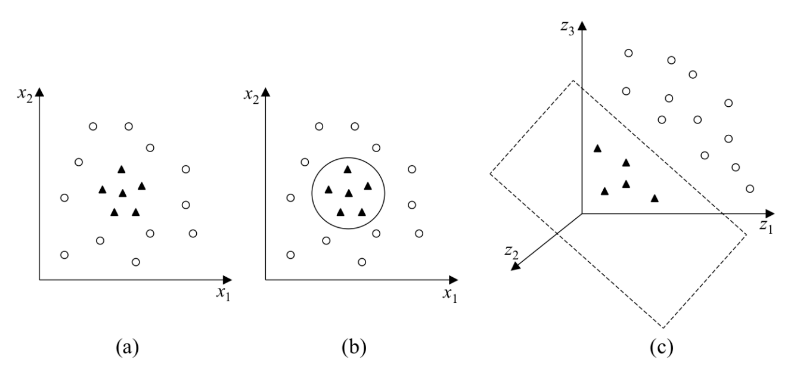 Para realizar a separação dos dados deste tipo de conjunto, a SVM mapea mapeia este conjunto de treinamento de seu espaço original para um novo espaço de maior dimensão, denotado de espaço de características. Este mapeamento permite que o conjunto seja separada através de uma SVM Linear. |
OpenCV
OpenCV é um biblioteca implementada para aplicações no campo de Aprendizado de Máquina e Visão Computacional. Desenvolvida seguindo o modelo de software livre (BSD licensed), o OpenCV provê 25000 algoritmos otimizados, dos quais incluem um amplo conjunto de classes e algoritmos capazes de reconhecer faces, identificar objetos, classificar ações em um vídeo, localizar movimentos, etc. OpenCV é utilizada extensivamente por empresas e instituições de pesquisa como Google, Yahoo, Microsoft, Intel, IBM, dos quais também participaram do desenvolvimento desta biblioteca. Uma das características essenciais é o suporte às linguagens C++, C, Python, Java e Matlab, além de possuir combatibilidade com sistemas Windows, Linux, Android e Mac OS[17].
Instalação
| Conteúdo |
|---|
|
Os passos seguintes para a instalação do OpenCV 3.0 foram realizados no sistemas operacional Ubunto 14.04 e utilizando a Python 3.4+. Todos os passos foram feitos baseados em[18] Passo 1 - Instalação dos Pré-requisitos Baixar informações e atualizar pacotes já instalados $ sudo apt-get update $ sudo apt-get upgrade Instalação de ferramentas de compilação do OpenCV 3.0 $ sudo apt-get install build-essential cmake git pkg-config Instalação de bibliotecas e pacotes para leitura de imagens $ sudo apt-get install libjpeg8-dev libtiff4-dev libjasper-dev libpng12-dev Instalação de bibliotecas e pacotes para leitura de vídeos $ sudo apt-get install libavcodec-dev libavformat-dev libswscale-dev libv4l-dev Instalação do GTK para uso das interfaces de usuário do OpenCV $ sudo apt-get install libgtk2.0-dev Instalação de pacotes utilizados para otimizar funções dentro do OpenCV sudo apt-get install libatlas-base-dev gfortran Passo 2 - Configurando Pyhton (Parte 1) Instalação do pip, um gerenciador de pacotes para o Python. Note que é necessário o python3 instalado corretamente no sistema. Caso você não forneça o python3, o pip será instalado para o Python 2.7, do qual não é a nossa intenção. $ wget https://bootstrap.pypa.io/get-pip.py $ sudo python3 get-pip.py Para o desenvolvimento em Python é uma boa prática trabalhar em um ambiente de desenvolvimento virtual. Para isso, utilizaremos os pacotes virtualenv e virtualenvwrapper que permitem criar um ambiente totalmente separado e independente. Utiize o pip3 para a instalação destes pacotes: $ sudo pip3 install virtualenv virtualenvwrapper Configurando os caminhos para nosso ambiente virtual. Dentro da pasta $HOME, edite o arquivo .bashrc, adicionando as seguintes linhas: export VIRTUALENVWRAPPER_PYTHON=/usr/bin/python3 export WORKON_HOME=$HOME/.virtualenvs Atualizando o bashrc $ source /usr/local/bin/virtualenvwrapper.sh $ source ~/.bashrc Criação do ambiente virtual. Para os próximos passos é importante que se esteja nesse ambiente virtual. $ mkvirtualenv cv Passo 2 - Configurando Pyhton (Parte 2) Instalação dos cabeçalhos e arquivos de desenvolvimento para o Python 3.4+ $ sudo apt-get install python3.4-dev O OpenCV representa as imagens através do NumPy. Instalação do NumPy no ambiente virtual cv. $ pip install numpy Passo 3 - Compilação e Instalação do OpenCV 3.0 Download dos arquivos $ cd ~ $ git clone https://github.com/Itseez/opencv.git $ cd opencv $ git checkout 3.0.0 $ cd ~ $ git clone https://github.com/Itseez/opencv_contrib.git $ cd opencv_contrib $ git checkout 3.0.0 Obs: A versão dos arquivos 3.0.0 pode ser alterada para a última para as mais recentes [14]. É importante que as versões do opencv e do opencvcontrib sejam as mesmas. Compilação $ cd ~/opencv
$ mkdir build
$ cd build
$ cmake -D CMAKE_BUILD_TYPE=RELEASE \
-D CMAKE_INSTALL_PREFIX=/usr/local \
-D INSTALL_C_EXAMPLES=ON \
-D INSTALL_PYTHON_EXAMPLES=ON \
-D OPENCV_EXTRA_MODULES_PATH=~/opencv_contrib/modules \
-D BUILD_EXAMPLES=ON \
-D INSTALL_C_EXAMPLES=OFF \
-D BUILD_opencv_xfeatures2d=OFF ..
$ make -j4 Obs: onde 4 é o número de cores disponíveis em seu processador. Instalação do OpenCV $ sudo make install $ sudo ldconfig Passo 4 - Links para OpenCV 3.0 Caso tenha alcançado esta etapa sem erros, o OpenCV 3.0 deve estar instalado em /usr/local/lib/python3.4/site-packages/. Entretanto, para realizar o seu uso dentro de nosso ambiente virtual, é necessário criar um link para o OpenCV. Para isso execute: $ cd ~/.virtualenvs/cv/lib/python3.4/site-packages/ $ ln -s /usr/local/lib/python3.4/site-packages/cv2.cpython-34m.so cv2.so Passo 5 - Teste O OpenCV foi instalado com sucesso! Para confirmar se a instalação está funcionando realize os seguintes passos: $ source /usr/local/bin/virtualenvwrapper.sh $ workon cv $ python >>> import cv2 >>> cv2.__version__ A resposta do último comando deve retornar a versão da biblioteca OpenCV que instalamos neste tutorial, conforme imagem abaixo: |
HOG
| Conteúdo |
|---|
|
Importando biblitecas. import numpy as np import cv2 Lendo imagem do disco im = cv2.imread('40km64x128.jpeg')
im = np.float32(im) / 255.0
cv2.imshow('image',im)
cv2.waitKey(0)
cv2.destroyAllWindows()
Convertendo imagem para escala cinza gray_image = cv2.cvtColor(im, cv2.COLOR_BGR2GRAY)
cv2.imshow('image',gray_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Convertendo valores da imagem para inteiros de 8 bits (necessário no hog.compute) gray_image = np.uint8(gray_image) Configurações do descritor HOG winSize = (64,128) # Size of the images in our dataset blockSize = (4,8) # The size of blocks (Illumination variance) blockStride = (5,5) # Determine the overlap between neighboring block cellSize = (4,8) # Size of the cells nbins = 9 # Numbs of positions in the histogram derivAperture = 1 # winSigma = -1. # histogramNormType = 0 # L2HysThreshold = 0.2 # gammaCorrection = 1 # nlevels = 64 # useSignedGradients = True # Signed (between 0 and 360) or unsigned (between 0 and 180) gradients hog = cv2.HOGDescriptor(winSize,blockSize,blockStride,cellSize,nbins,derivAperture,winSigma,histogramNormType,L2HysThreshold,gammaCorrection,nlevels, useSignedGradients) Obtendo descritor HOG da imagem descriptor = hog.compute(gray_image) |
SVM
| Conteúdo |
|---|
|
Criação e configuração da SVM svm = cv2.ml.SVM_create() svm.setType(cv2.ml.SVM_C_SVC) svm.setKernel(cv2.ml.SVM_RBF) # Set SVM Kernel to Radial Basis Function (RBF) svm.setC(C) svm.setGamma(gamma) Treinamento da SVM
svm.train(trainData, cv2.ml.ROW_SAMPLE, trainLabels)
svm->save("digits_svm_model.yml");
Testes testResponse = svm.predict(testData)[1].ravel() |
Matlab
| Conteúdo |
|---|
|
Objetivo: extrair o histrograma de gradientes orientados de uma imagem e estudar o procedimento. x = imread('imagem1.jpeg');
figure(1);
imshow(x);
 %% Binarização da imagem x = x(:,:,1) >= 175; figure(2); imshow(x);  %% Extração HOG's [featureVector,hogVisualization] = extractHOGFeatures(x); figure(3); subplot(1,2,1); imshow(x); subplot(1,2,2); plot(hogVisualization);  |
Notas
Referências
- ↑ 1,0 1,1 COUTINHO, D.P.; MARROQUIM R. SIFT - Scale Invariant Feature Transform. LCG Computer Graphics Lab, Universidade Federal do Rio de Janeiro, 2013
- ↑ 2,0 2,1 2,2 BELO, F. A. Desenvolvimento de Algoritmos de Exploração e Mapeamento Visual para Robôs Móveis de Baixo Custo. Diss. PUC-Rio, 2006.
- ↑ VARELLA, C. A. Análise de componentes principais. Universidade Federal Rural do Rio de Janeiro, Seropédica, 2008
- ↑ SOLOMON, Chris; BRECKON, Toby. Fundamentals of Digital Image Processing: A practical approach with examples in Matlab. John Wiley & Sons, 2011.
- ↑ 5,0 5,1 5,2 5,3 GONZALEZ, Rafael C.; WOODS, Richard C. Processamento digital de imagens, Tradução: Cristina Yamagami e Leonardo Piamonte. 3ª Edição. São Paulo: Pearson. 2010
- ↑ 6,0 6,1 6,2 MARQUES, Ogé F.; VIEIRA Hugo.Processamento Digital de Imagens. Rio de Janeiro: Brasport. 1999
- ↑ GONZALEZ, Rafael C.; WOODS, Richard E.; EDDINS, Steven L.Digital image processing using MATLAB. 2º Edition. India: McGraw. 2010.
- ↑ 8,00 8,01 8,02 8,03 8,04 8,05 8,06 8,07 8,08 8,09 8,10 LORENA, Ana Carolina; CARVALHO, André. Uma introdução às Support Vector machines. Revista de Informática Teórica e Aplicada, 2007, 14.2: 43-67.
- ↑ 9,0 9,1 9,2 9,3 9,4 9,5 9,6 9,7 9,8 SANTOS, Eulanda M.Teoria e aplicação de support vector machines à aprendizagem e reconhecimento de objetos baseado na aparência. 2002. Tese de Doutorado. Universidade Federal da Paraíba. Disponível em [1].Acessado em 9 de Setembro de 2017.
- ↑ MÜLLER, Andreas C.; GUIDO, Sarah. Introduction to machine learning with Python: a guide for data scientists. 2017.
- ↑ 11,0 11,1 11,2 11,3 ALPAYDIN, Ethem.Introduction to machine learning. MIT press, 2014
- ↑ 12,0 12,1 12,2 12,3 12,4 MONARD, Maria Carolina; BARANAUSKAS, José Augusto. 'Conceitos sobre aprendizado de máquina. Sistemas Inteligentes-Fundamentos e Aplicações, v. 1, n. 1, 2003. Disponível em [2]. Acessado em 31 de Agosto de 2017.
- ↑ 13,0 13,1 CAMASTRA, Francesco; VINCIARELLI, Alessandro. Machine learning for audio, image and video analysis. Advanced Information and Knowledge Processing, p. 83-89, 2008.
- ↑ CAMILO, Cássio Oliveira; SILVA, João Carlos da. Mineração de dados: Conceitos, tarefas, métodos e ferramentas. Universidade Federal de Goiás (UFC), 2009, 1-29.Disponível em [3]. Acessado em 24 de Agosto de 2017
- ↑ 15,0 15,1 15,2 15,3 15,4 HAYKIN, Simon. Redes neurais: princípios e prática. Bookman Editora, 2001.
- ↑ SLOUGHTER, Dan. The calculus of functions of several variables. D. Sloughter, 2001.
- ↑ OpenCV. Disponível em [4]. Acessado em 16 de Agosto de 2017
- ↑ ROSEBROCK, Adrian. Install OpenCV 3.0 and Python 3.4+ on Ubuntu. Pyimagesearch. 2015. Disponível em [5]. Acessado em 16 de Agosto de 2017.


















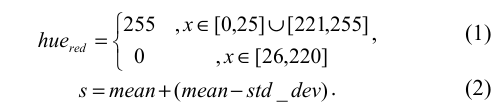

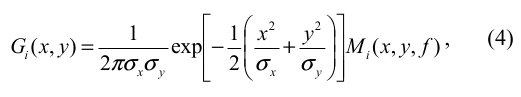





























![{\displaystyle [0,L-1]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/519ec65a9436d3a0094d9c7df1fb388723f0098f)




























