Python 2021 Mod5
1 Módulo 5: Usos e Aplicações de Bibliotecas
- Objetivos de aprendizagem
- Aplicar a biblioteca Math para resolver funções matemáticas.
- Aplicar as bibliotecas Numpy, Matplotlib, e Scipy para análise de dados e geração de gráficos
- Aplicar o framework Flask para desenvolvimento web e entender a relação com o HTML.
1.1 Math
Funções matemáticas comuns, tais como valor absoluto, exponencial ou log, são definidas dentro da biblioteca matemática.
Funções adicionais e especificações da Biblioteca Math podem ser encontradas AQUI.
Veja abaixo exemplos de como utilizar a biblioteca Math.
import math
# Função de potência
print("2^5 = " + str(math.pow(2,5)))
2^5 = 32.0
# Função Teto
print(math.ceil(3.45))
print(math.ceil(10.01))
4 11
# Função Piso
print(math.floor(5.25))
print(math.floor(11.01))
5 11
# Valor Absoluto
print(math.fabs(-10.33))
print(math.fabs(5.25))
10.33 5.25
# Log com base "e", ou log natural
print(math.log(1000))
6.907755278982137
# Log com uma base específica no valor de 10
print(math.log(1000,10))
2.9999999999999996
1.2 Análise de dados com Numpy, Matplotlib, Scipy
Numpy é um pacote para computação numérica em Python.
- Fornece uma estrutura de dados eficiente para matrizes numéricas, n-dimensionais (ndarray)
- Suporta operações vetoriais e matriciais.
- O Numpy é implementado em C, portanto é realmente rápido e eficiente.
O formato básico de dados em Numpy é a matriz n-dimensional. Estas podem ser usadas para representar vetores (1D), matrizes (2D) ou tensores (nD).
- Uma matriz numérica de uma dimensão é frequentemente usada para representar uma série de dados.
- As matrizes n-dimensionais muitas vezes representam conjuntos completos de dados (cada coluna é um tipo de medida).
- As matrizes numéricas são muito parecidas com as listas de Python. A indexação e o fatiamento funcionam da mesma forma (incluindo atribuições). No entanto, todas as células de uma mesma matriz devem conter o mesmo tipo de dados.
Os operadores não trabalham da mesma forma para listas e matrizes e há muitos métodos adicionais definidos nelas.
Referenciado pelo professor Daniel Bauer da Universidade de Columbia CS, Palestra ENGI1006
# Vamos ver o que acontece se usarmos uma lista para representar um vetor?
[1,2,3] * 3
[1, 2, 3, 1, 2, 3, 1, 2, 3]
# Anteriormente, NÃO foi o resultado esperado com multiplicação vetorial por um escalar
# É preciso fazer isto
[i*3 for i in [1,2,3]]
[3, 6, 9]
# E quanto à soma de dois vetores?
# Tratado como concatenação de lista
[1,2,3]+[4,5,6]
[1, 2, 3, 4, 5, 6]
# Soma de dois vetores
a = [1,2,3]
b = [4,5,6]
[a[i] + b[i] for i in range(len(a))]
[5, 7, 9]
# Produto vetorial ou produto escalar?
[1,2,3] * [4,5,6]
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-6-a661702feff9> in <module>()
1 # cross product or dot product?
----> 2 [1,2,3] * [4,5,6]
TypeError: can't multiply sequence by non-int of type 'list'
# Poderíamos calcular o produto escalar assim:
u = [1,2,3]
v = [4,5,6]
total = 0
for i in range(len(u)):
total += u[i] * v[i]
total
32
# Vamos ver o que acontece se usarmos Numpy
# np é uma convenção comum para se referir a Numpy ao longo de todo o código
import numpy as np
u = np.array([1,2,3])
v = np.array([4,5,6])
# dot() calcula o produto escalar de dois vetores
np.dot(u,v)
32
type(u)
numpy.ndarray
print(u)
[1 2 3]
# Mais algumas operações em matrizes 1D:
import numpy as np
u = np.array([1,2,3])
v = np.array([4,5,6])
print("Vector addition with another vector ---> " + str(u+v))
print("Vector addition with a scalar ---> " + str(u+4))
print("Vector multiplication by a scalar ---> " + str(u * 4))
print("Vector multiplication (NOT dot nor cross product) ---> " + str(u * v))
print("Vector sum ---> " + str(np.sum(u * v)))
print("Dot product ---> " + str(np.dot(u,v)))
Vector addition with another vector ---> [5 7 9] Vector addition with a scalar ---> [5 6 7] Vector multiplication by a scalar ---> [ 4 8 12] Vector multiplication (NOT dot nor cross product) ---> [ 4 10 18] Vector sum ---> 32 Dot product ---> 32
"""
Vejamos as matrizes multidimensionais: 'matrizes dentro de matrizes'.
O seguinte código cria um total de três matrizes 3*3 com todas elas
"""
u = np.ones((3,3,3))
u
array([[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]])
# Retornar a forma/dimensão da matriz
u.shape
(3, 3, 3)
np.ones((2,3))
array([[1., 1., 1.],
[1., 1., 1.]])
np.ones((3, 2))
array([[1., 1.],
[1., 1.],
[1., 1.]])
Scipy é um pacote para analisar o ajuste da curva.
Matplotlib é um pacote para dados gráficos.
Veja a seguir um exemplo de como o Scipy, o Numpy e o Matplotlib poderiam ser usados juntos na análise de dados.
Documentações para Scipy, Matplotlib e Numpy podem ser acessadas AQUI.
# Importar diferentes pacotes usados para análise de dados
# ... "as opt" significa que o programador poderia usar a abreviatura de "opt" para se referir a esta biblioteca, em vez de digitar o nome completo
import scipy.optimize as opt
import numpy as np
import matplotlib.pyplot as plt
# Dados brutos inseridos manualmente pelo usuário
I =[4.0, 3.5, 3.0, 2.5, 2.0]
B =[1.31, 1.14, 0.97 ,0.81, 0.76]
IError = [0.2, 0.2, 0.2, 0.2, 0.2]
BError = [0.03, 0.02, 0.04, 0.02, 0.05]
print("estimated B for each error \n")
for i in range (5) :
print(str(I[i]) + "+-" + str(IError[i]) + ": " + str(B[i]) + "+-" + str(BError[i]))
# Aplicar a biblioteca Numpy para formatar a lista de dados brutos em uma matriz multidimensional
# Isto é necessário para a otimização das funções e para o uso adequado do pacote Scipy
xdata = np.array(I)
ydata = np.array(B)
xerror = np.array(IError)
yerror= np.array(BError)
# Definir função linear para ajuste
def func(h, m, b):
return m*h + b
# w dá o parâmetro estimado para m e b, armazenado na matriz quadrada de w e u
# A informação que falta _ retornar sobre variância e covariância
# w é uma matriz com informações sobre o valor da inclinação e do y-intercepção
w, u = opt.curve_fit(func, xdata, ydata)
# Aplicar coordenadas x e resultado otimizado sobre o ajuste da curva para encontrar a "Linha do Melhor Ajuste".
yfit = func(xdata,*w)
# Use o pacote Matplotlib para fazer gráficos de dados
# 1. Gráfico das barras de erro para cada valor x
# 2. Gráfico da "Linha do Melhor Ajuste"
# Nota: há opções para personalizar o visual de seu gráfico com diferentes parâmetros
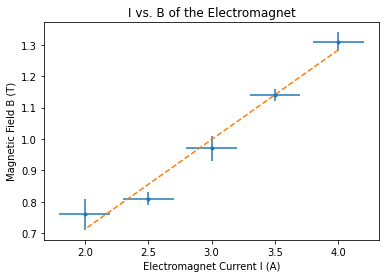
plt.errorbar(I, B, xerr=IError, yerr = BError, fmt='o', ms = 3)
plt.plot(xdata,yfit,label="Fit", linewidth=1.5, linestyle='dashed')
# Adicionar título e etiquetas ao gráfico
plt.title('I vs. B of the Electromagnet')
plt.xlabel('Electromagnet Current I (A)')
plt.ylabel('Magnetic Field B (T)')
print("\n Estimated parameters of m and b: ", w)
print("\n Estimated variance of m & b: ", np.sqrt(np.diag(u)))
# Se necessário, é assim que você poderia salvar o gráfico em sua máquina local.
# Mas aqui NÃO precisamos salvar o gráfico, por isso comentaremos esta linha.
# Especifique o nome da imagem como o parâmetro
### plt.savefig('IvsB.jpg')
# Nota: se você estiver mostrando e armazenando o gráfico, certifique-se de SALVAR antes de PROJETAR.
plt.show()
estimated B for each error 4.0+-0.2: 1.31+-0.03 3.5+-0.2: 1.14+-0.02 3.0+-0.2: 0.97+-0.04 2.5+-0.2: 0.81+-0.02 2.0+-0.2: 0.76+-0.05 Estimated parameters of m and b: [0.286 0.14 ] Estimated variance of m & b: [0.02778489 0.08563877]
1.3 Desenvolvimento Web com Flask
Flask é uma estrutura Python para a construção de uma aplicação web.
Assista a este vídeo Introdução ao Flask de como construir um site básico com o Flask.
"""
app.route define a URL e qual a função a ser executada para cada URL.
Quando apenas '/' é especificado na URL, presume-se que seja a página inicial.
Esta aplicação web fornecerá o texto '<h1>WELCOME to My Home Page</h1>'.
no estilo cabeçalho 1.
Quando a URL contém um nome na URL, o nome da URL é analisado para ser usado
na função que serve a página web. Esta é conhecida como uma "página web dinâmica".
Quando o admin é específico na URL, o admin() será executado para
redirecionar a página para mostrar a página inicial.
Consulte as imagens abaixo para obter uma visão de como é cada página.
"""
# Importar pacotes
from flask import Flask, redirect, url_for
app = Flask(__name__)
@app.route("/")
def home():
return "<h1>WELCOME to My Home Page</h1>"
@app.route("/<name>")
def user(name):
return f"<h3>Hello, nice to meet you {name}!</h3>"
@app.route("/admin")
def admin():
return redirect(url_for("home"))
if __name__ == "__main__":
app.run()
- * Serving Flask app "__main__" (lazy loading)
- * Environment: production
- WARNING: This is a development server. Do not use it in a production deployment.
- Use a production WSGI server instead.
- * Debug mode: off
- * Running on http://127.0.0.1:5000/ (Press CTRL+C to quit)
- Vista da página inicial
- Vista dinâmica da página com o nome "Mary" na URL
A página Admin é a MESMA da página inicial, porque a página de Admin é redirecionada para a página inicial.