Sistemas de Numeração

Os números podem ser representados em qualquer sistema de numeração.

Os seres humanos usam normalmente um sistema de numeração baseado na base 10 (com 10 dígitos diferentes).

Os computadores, pelo fato de só representarem dois valores (0, 1), os dígitos binários - também conhecidos por bits, da contração do inglês binary digit - são máquinas binárias, e por isso trabalham em base 2.

A ordem de um dígito dentro de um número é dada pela posição que esse dígito ocupa no número: 0 é a ordem do dígito imediatamente à esquerda do ponto (vírgula) decimal, crescendo no sentido da esquerda, e decrescendo no sentido da direita.

Exemplo

1532.64
Dígito 4 - ordem -2
Dígito 6 - ordem -1
Dígito 2 - ordem 0
Dígito 3 - ordem +1
Dígito 5 - ordem +2
Dígito 1 - ordem +3

A base utilizada determina o número de dígitos que podem ser utilizados; por exemplo, base 10 utiliza 10 dígitos (0 a 9), base 2 utiliza 2 dígitos (0 e 1), base 5 utiliza 5 dígitos (0 a 4), base 16 utiliza 16 dígitos (0 a 9, e A a F).

Conversão entre bases

A conversão de um número escrito na base b para a base decimal obtém-se multiplicando cada dígito pela base b elevada à ordem do dígito, e somando todos estes valores.

Exemplos

1532 (base 6)
1*6^3 + 5*6^2 + 3*6^1 + 2*6^0 = 416d

1532.64 (base 10)
1*10^3 + 5*10^2 + 3*10^1 + 2*10^0 + 6*10^-1 + 4*10^-2 = 1532.64d

1532 (base 13)
1*13^3 + 5*13^2 + 3*13^1 + 2*13^0 = 3083d

110110.011 (base 2)
1*2^5 + 1*2^4 + 0*2^3 + 1*2^2 + 1*2^1 + 0*2^0 + 0*2^-1 + 1*2^-2 + 1*2^-3 = 54.375d

Na conversão de um número na base decimal para uma base b, o processo mais directo é composto por 2 partes:

divisão sucessiva da parte inteira desse número pela respectiva base, sendo os restos obtidos

com cada uma dessas divisões, os dígitos da base b (a começar com o menos significativo, i.e., mais junto ao ponto decimal) e os quocientes a usar na sucessão de divisões;

multiplicação sucessiva da parte fraccionária desse número pela respectiva base, sendo a parte

inteira de cada um dos produtos obtidos, os dígitos da base b (a começar com o mais significativo, i.e., mais junto ao ponto decimal), e a parte decimal a usar na sucessão de multiplicações.

Exemplo

235.375d
235/2 = 117 Resto = 1 /* bit menos significativo int*/
117/2 = 58 Resto = 1
58/2 = 29 Resto = 0
29/2 = 14 Resto = 1
14/2 = 7 Resto = 0
7/2 = 3 Resto = 1
3/2 = 1 Resto = 1 /* bit mais significativo int*/
0.375*2 = 0.750 P. int. = 0 /* bit mais significativo frac*/
0.75*2 = 1.5 P. int. = 1
0.5*2 = 1.0 P. int. = 1 /* bit menos significativo frac*/
235.37510 = 11101011.011b

Outro processo de converter de uma base decimal para outra base utiliza subtrações sucessivas, mas apenas é utilizado na conversão para a base binária, e mesmo nesta para valores que não ultrapassam a ordem de grandeza dos milhares e normalmente apenas para inteiros.

A grande vantagem deste método é a sua rapidez de cálculo mental, sem ajuda de qualquer máquina de calcular, desde que se saiba de cor a “tabuada” das potências de 2:

Tabela de Potências de 2:
2⁰ 2¹ 2² 2³ 2⁴ 2⁵ 2⁶ 2⁷ 2⁸ 2⁹

1 2 4 8 16 32 64 128 256 512

Ajuda também saber como se comportam as potências de 2 para expoentes com mais que um dígito.

Sabendo que 2¹⁰ = 1024 (= 1k, ~= 10³ ), e que 2¹ⁿ

= 2^n * 2^10 = 2^n * 1k, é possível a partir daqui extrapolar

não apenas todos os restantes valores entre 2^10 e 2^19, como ainda ter uma noção da ordem de grandeza de um valor binário com qualquer número de dígitos (bits) 1:

Exemplos

Tabela de potências de 2¹⁰ a 2¹⁹:
2¹⁰ 2¹¹ 2¹² 2¹³ 2¹⁴ 2¹⁵ 2¹⁶ 2¹⁷ 2¹⁸ 2¹⁹

1k 2k 4k 8k 16k 32k 64k 128k 256k 512k

Tabela de potências de 2 com expoentes de 10 em 10:
2¹⁰ 2²⁰ 2³⁰ 2⁴⁰ 2⁵⁰ 2⁶⁰ 2⁷⁰ 2⁸⁰ 2⁹⁰ 2¹⁰⁰

1 kilo 1 Mega 1 Giga 1 Tera 1 Peta 1 Exa 1 Zeta 1 Yota 1 ???? 1 ????

~10³ ~10⁶ ~10⁹ ~10¹² ~10¹⁵ ~10¹⁸ ~10²¹ ~10²⁴ ~10²⁷ ~10^30*

Com base nesta informação, é agora possível pôr em prática o método das subtrações sucessivas para converter um nº decimal num binário: procura-se a maior potência de 2 imediatamente inferior ao valor do nº decimal, e subtrai-se essa potência do nº decimal; o expoente da potência indica que o nº binário terá um bit 1 nessa ordem; com o resultado da subtração repete-se o processo até chegar ao resultado 0.

Exemplo

1081.625d
1081.625 - 2^10 = 57.625
57.625 - 2^5 = 25.625
25.625 - 2^4 = 9.625
9.625 - 2^3  = 1.625
1.625 - 2^0 = 0.625
0.625 - 2^-1 = 0.125
0.125 - 2^-3 = 0

 1 0 0 0 0 1 1 1 0 0 1. 1 0 1 na base binária
10 9 8 7 6 5 4 3 2 1 0 -1-2–3 < ordem

Os processadores utilizam um determinado número de bits para representar um número.

A quantidade de bits utilizados determina a gama de valores representáveis. Tal como qualquer outro sistema de numeração - onde a gama de valores representáveis com n dígitos é b n - a mesma lógica aplica-se à representação de valores binários.

Sendo n o número de bits utilizados, a gama de valores representáveis em binário, usando n bits é 2^n

Representação de Inteiros

Base hexadecimal

O sistema de numeração de base hexadecimal (16) é frequentemente utilizado como forma alternativa de representação de valores binários, não apenas pela facilidade de conversão entre estas 2 bases, como ainda pela menor probabilidade de erro humano na leitura/escrita de números.

Tal como referido anteriormente, são utilizados 16 dígitos: 0, 1, ..., 9, A, B, C, D, E, F.

Exemplos

4312d em hexadecimal
4312 / 16 = 269 Resto = 8
269 / 16 = 16 Resto = 13 (dígito D)
16 / 16 = 1 Resto = 0
1 / 16 = 0 Resto = 1

Logo, 4312d = 10D8h

2AF3h em decimal
2 * 16^3 + 10 * 16^2 + 15 * 16^1 + 3 * 16^0 = 10995d

A motivação para usar hexadecimal é a facilidade com que se converte entre esta base e binário.

Cada dígito hexadecimal representa um valor entre 0 e 15; cada conjunto de 4 bits representa também um valor no mesmo intervalo.

Pode-se então aproveitar esta característica nos 2 tipos de conversão: de binário, agrupando os bits de 4 em 4 a partir do ponto decimal, e convertendo-os; para binário, convertendo cada dígito hexadecimal em 4 bits.

Exemplos

  2    A    F (hexadecimal)
0010 1010 1111 (binário)
2AFh = 001010101111b

1101 0101 1011 (binário)
 D    5    B (hexadecimal)
110101011011b = D5Bh (também comum representar como 0xD5B, ou ainda 0xd5b )

Números negativos

Os computadores lidam com números positivos e números negativos, sendo necessário encontrar uma representação para números com sinal negativo.

Existe uma grande variedade de opções, das quais apenas se destacam 4, sendo apenas 3 as atualmente usadas para representar valores negativos:

sinal e amplitude/magnitude (S+M)
complemento para 1
complemento para 2
notação em excesso (ou biased)

Sinal e Amplitude

Como o próprio nome indica, a representação sinal e amplitude utiliza um bit para representar o sinal, o bit mais à esquerda:

MSB: 0 para indicar um valor positivo, 1 para indicar um valor negativo.
(N-1) bits restantes: módulo do número
Números representáveis:

 -2^(N-1)-1 ≤ X ≤ 2^(N-1)-1

Por exemplo: N = 8, -127 ≤ X ≤ 127

Exemplos:

+45d = 0 0101101b (em 8 bits)

-25d = 1 0011001b (em 8 bits)

00101010b = +42d

10101010b = -42d

Complemento 1

Na representação em complemento para 1 invertem-se todos os bits de um número para representar o seu complementar: assim se converte um valor positivo para um negativo, e vice-versa.

Quando o bit mais à esquerda é 0, esse valor é positivo; se for 1, então é negativo.

MSB:
- valor 0: sinal +;
- valor 1: sinal -
(N-1) bits restantes: módulo do número
O simétrico é o complemento de 1
Faixa representável: mesmo que MS: -2^(N-1)-1 ≤ X ≤ 2^(N-1)-1

Exemplos

100d = 01100100b (com 8 bits)
Invertendo todos os bits:
10011011b = –100d

00101010b = +42d
11010101b = -42d

O problema desta representação é que existem 2 padrões de bits para o 0. Ou seja:

0d = 00000000b = 11111111b

Complemento 2

A solução encontrada consiste em representar os números em complemento 2. Para determinar o negativo de um número negam-se todos os seus bits e soma-se uma unidade.

MSB: O bit mais à esquerda representa o sinal
- valor 0: sinal +;
- valor 1: sinal -
(N-1) bits restantes: módulo do número
Simétrico em dois passos
- Passo 1: calcula-se C-1
- Passo 2: Soma-se 1 a esse C-1. Despreza-se transporte no último, caso exista
Quantidade representável assimétrica: -2^(N-1) ≤ X ≤ 2^(N-1)-1

Exemplo

100d = 01100100b (com 8 bits)
Invertendo todos os bits:
10011011b
Somando uma unidade :
10011011b + 1 = 10011100b = –100d

A representação em complemento 2 tem as seguintes características:

o bit da esquerda indica o sinal;
o processo indicado no parágrafo anterior serve para converter um número de positivo para negativo

e de negativo para positivo;

o 0 tem uma representação única: todos os bits a 0;
a gama de valores que é possível representar com n bits é -2^(n-1) ... 2^(n-1)-1.

Exemplo

Qual o número representado por 11100100b (com 8 bits)?
Como o bit da esquerda é 1 este número é negativo.
Invertendo todos os bits:
00011011b
Somando uma unidade :
00011011b + 1 = 00011100b = 28d
Logo:
11100100b = –28d

Como é que se converte um número representado em complemento para 2 com n bits, para um número representado com mais bits?

Resposta: basta fazer a extensão do sinal! Este método também é chamado de "sliding 1"'.

Se o número é positivo acrescenta-se 0's à esquerda, se o número é negativo acrescenta-se 1's à esquerda.

Exemplo

Representar os seguintes números (de 8 bits) com 16 bits:

01101010b
Positivo, logo:
00000000 01101010b

11011110b
Negativo, logo:
11111111 11011110b

A multiplicação e a divisão têm algoritmos complexos que não convém explorar nesta disciplina. No entanto a multiplicação e a divisão especificamente por potências de 2 realizam-se efetuando deslocamentos de bits à direita ou à esquerda, respectivamente.

Isto é, fazer o deslocamento à esquerda uma vez - num número binário - corresponde a multiplicar por 2, duas vezes corresponde a multiplicar por 4 (= 2²), 3 vezes corresponde a multiplicar por 8 (= 2³), e assim sucessivamente.

O mesmo se aplica à divisão com o deslocamento à direita.

Exemplo

Dividir 11001010b (= 202d ) por 4:
Deslocar à direita 2 vezes:
00110010.1b = 50.5d

Multiplicar 00001010b (= 10d ) por 8.
Deslocar à esquerda 3 vezes:
01010000b = 80d

Esta regra também se aplica aos números em complemento para 2 desde que se mantenha o sinal.

OBSERVAÇÃO: O Algoritmo FFT (fast fourier transform) aproveita desta característica da notação complemento 2, para implementar muito rapidamente uma versão digital da Transformada de Fourier Contínua.

Notação em Excesso

A última notação referida no início tem uma vantagem sobre qualquer outra referida anteriormente: a representação numérica dos valores em binário, quer digam respeito a valores com ou sem sinal, tem o mesmo comportamento na relação entre eles.

Em outras palavras, o valor em binário com todos os bits a 0 representa o menor valor inteiro, quer este tenha sinal ou não, e o mesmo se aplica ao maior valor em binário, i.e., com todos os bits a 1: representa o maior inteiro, com ou sem sinal.

Exemplo

Binário (8 bits) Sinal + Ampl Compl p/1 Compl p/2 Excesso (128)

0 0 0 0 0 0 0 1₂ +1 +1 +1 -127

1 0 0 0 0 0 0 1₂ -1 -126 -127 +1

1 1 1 1 1 1 1 0₂ -126 -1 -2 +126

Como o próprio nome sugere, esta codificação de um inteiro (negativo ou positivo) em binário com n bits é feita sempre em excesso (de 2^(n-1) ou 2^(n-1)-1). Neste exemplo com 8 bits, o valor +1d é representado em binário, em notação por excesso de 2^n-1, pelo valor (+1d + excesso) = (+1d + 128d) = (0000 0001b + 1000 0000b) = 1000 0001b.

A tabela que a seguir se apresenta, representando todas as combinações possíveis com 4 bits, ilustra de modo mais completo as diferenças entre estes 4 modos (+1 variante) de representar inteiros com sinal.

Binário (8 bits) Sinal + Ampl Compl p/1 Compl p/2 Excesso (7) Excesso (8)

0 0 0 0 0 0 0 -7 -8

0 0 0 1 1 1 1 -6 -7

0 0 1 0 2 2 2 -5 -6

0 0 1 1 3 3 3 -4 -5

0 1 0 0 4 4 4 -3 -4

0 1 0 1 5 5 5 -2 -3

0 1 1 0 6 6 6 -1 -2

0 1 1 1 7 7 7 0 -1

1 0 0 0 -0 -7 -8 1 0

1 0 0 1 -1 -6 -7 2 1

1 0 1 0 -2 -5 -6 3 2

1 0 1 1 -3 -4 -5 4 3

1 1 0 0 -4 -3 -4 5 4

1 1 0 1 -5 -2 -3 6 5

1 1 1 0 -6 -1 -2 7 6

1 1 1 1 -7 -0 -1 8 7

Exercício Represente os números +57 e -57 na notação Excesso 64.

Solução: A notação Excesso 64 vai permitir representar-se valores entre -(2⁶) até +(2⁶) - 1, isto é: -64 a +63, por meio do cálculo:

+57d + 64d = 121d = 111 1001b

e

-57d + 64d = 7d = 000 0111b

Overflow

Ocorre sempre que o resultado de uma operação não pode ser representado no hardware disponível.

Overflow é um "estouro" da magnitude de um valor, no número limitado de bits de uma máquina.

Exemplos:

Adição de 2 operandos positivos (8 bits):

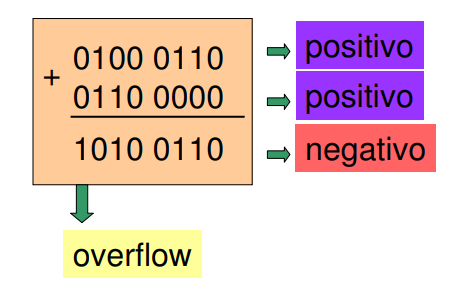
Figura 1 - Adição de 2 operandos positivos de 8 bits.

Um registrador de 8 bits só pode representar valores entre -128 até +127.

Ou seja, 0100 0110b (=70d) + 0110 0000 (=96d), que deveria resultar em +166d (estouro positivo), vai ser interpretado pelo computador como:

C2(1010 0110b) = 01011001b = -89d

Isto significa que o resultado estará correto, somente se o bit de sinal for ignorado.

Adição de 2 operandos negativos (8 bits):

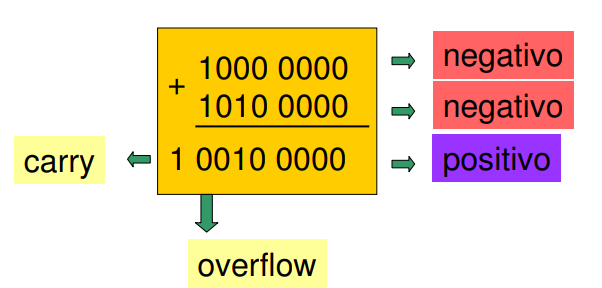
Figura 2 - Adição de 2 operandos negativos de 8 bits.

Ou seja, 1000 0000b (=-128d) + 1010 0000 (=-96d), que deveria resultar em -224d (estouro negativo), vai ser interpretado pelo computador como:

←[1] 0010 0000b = +32d

Isto significa que o resultado deu negativo, como esperado e em complemento a 2, mas não "coube" na palavra em questão, sendo interpretado, então, como positivo.

Por outro lado, existem casos em que não haverá problema:

Adição de operandos com sinais opostos (8 bits):

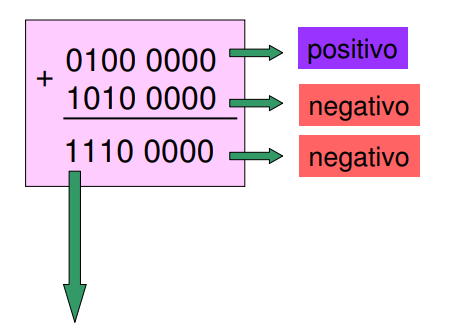
Figura 3 - Adição de 2 operandos com sinais opostos e resultado negativo.

Ou seja, +64d + (-96) = -32. Aqui, ocorreu uma subtração, de fato, não resultando em "estouro" da magnitude.

Não ocorreu overflow, e, como esperado, o resultado é negativo e está em complemento a 2!

Adição de operandos com sinais opostos (8 bits)

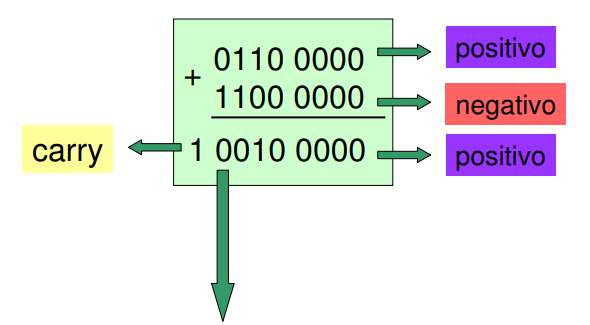
Figura 4 - Adição de 2 operandos com sinais opostos e resultado positivo.

Ou seja, +96 + (-64) = +32. Novamente ocorreu uma subtração de magnitudes, de fato.

Não ocorreu overflow, o carry é ignorado e o resultado está correto e é positivo.

Resumindo-se, as situações aonde podem acontecer overflow são:

Operação Operando A Operando B Resultado

A+B >=0 >=0 <0

A+B <0 <0 >=0

A-B >=0 <0 <0

A-B <0 >=0 >=0

Na ocorrência de overflow: a máquina precisa decidir como tratá-lo.

Linguagem C: não toma conhecimento do overflows. A tarefa é do programador.
FORTRAN: trata o overflow

Representação de Reais

A utilização da notação de ponto flutuante é muito grande em computadores, tanto para cálculos matemáticos com precisão, renderização de imagens digitais (criação de imagens pelo computador) entre outros. Os processadores atuais se dedicam muito em aperfeiçoar a técnica de seus chips para a aritmética de ponto flutuante, devido à demanda de aplicativos gráficos e jogos 3D que se utilizam muito deste recurso.

Nesta subseção iremos descrever os fundamentos da aritmética de ponto flutuante, para isso, serão apresentados alguns conceitos básicos, que juntamente com os conceitos da seção anterior, servirão para o entendimento do processo desta aritmética em um sistema computacional.

O primeiro ponto a ser discutido, é o motivo da criação da Notação de Ponto Flutuante, já que nas discussões anteriores já tínhamos trabalhado com a representação de números não inteiros utilizando a Notação de Ponto Fixo:

Figura 5 - Exemplo de notação de ponto flutuante.

O maior problema do Ponto Fixo é que o tamanho da parte inteira e da fracionária fica fixo com relação a seu armazenamento em memória.

Figura 6 - Limitação da notação de ponto flutuante.

Logo, para números com a parte apenas inteira, a região alocada para tratar a parte fracionária será inutilizada e vice-versa. Para evitar este desperdício criou-se a Notação de Ponto Flutuante.

Ponto Flutuante

Vamos explicar a notação de ponto flutuante por meio de um exemplo que emprega somente um byte de memória.

Primeiramente, escolhemos o MSB do byte para ser o bit de sinal do número. Um ‘0’ neste bit significa que o valor representado é positivo, enquanto o ‘1’ indica que é negativo.

Em seguida dividimos os sete bits restantes em dois grupos, o campo de expoente e o campo da mantissa, como mostrado na Figura 7:

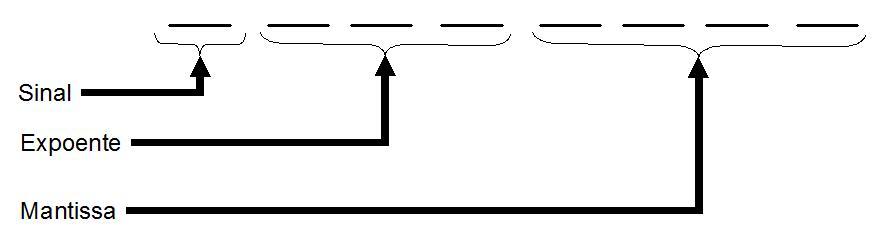
Figura 7 - Divisão de 1 byte nos campos da Notação de Ponto Flutuante.

Exemplo

Seja um byte contendo o padrão de bits 01101011.

Interpretando este padrão no formato que acabamos de definir, constatamos que:

o bit de sinal é ‘0’,
o expoente é ‘110’,
e a mantissa é ‘1011’.

Para decodificarmos o byte, extraímos primeiro a mantissa e colocamos o ponto binário à sua esquerda, obtendo:

.1011

Em seguida, extraímos o conteúdo do campo do expoente e o interpretamos como um inteiro codificado em três bits pelo método de representação de excesso, o qual é 110, nos dando o número positivo 2:

Valor Binário
(Notação de Excesso) Valor Representado

000 -4

001 -3

010 -2

011 -1

100
(centro) 0

101 1

110 2

111 3

Isto indica que devemos deslocar o ponto binário dois bits à direita (um expoente negativo codifica um deslocamento para a esquerda do ponto binário com a adição do valor 0).

Como resultado temos:

10.11

Que representa, na Notação de Ponto Fixo:

= 1×2^1 + 0×2^0 + 1×2^-1 + 1×2^-2
= 2+0+0,5+0,25 = 2,75

Em seguida, notamos que o bit de sinal do nosso exemplo é 0, assim, o valor representado é positivo e igual a +2,75.

O uso da notação de excesso para representar o expoente no sistema de Ponto Flutuante se dá pela possibilidade de comparação relativa das amplitudes de dois valores, apenas pelo emparelhamento das suas representações, da esquerda para a direita, em busca do primeiro bit em que os dois diferem.

Assim, se ambos os bits de sinal forem iguais a ‘0’, o maior dos dois valores é aquele que apresentar, da esquerda para a direita, um ‘1’ no bit em que os padrões diferem, logo ao comparar:

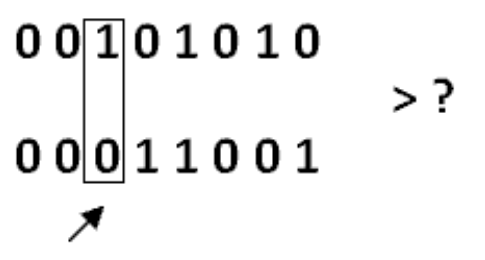
Figura 8 - Identificando do maior de dois valores digitais de mesmo padrão.

Conclui-se que o primeiro padrão é maior que o segundo, sem haver a necessidade de decodificar as representações em Ponto Flutuante, tarefa que seria mais custosa.

Quando os bits de sinal forem iguais a ‘1’, o maior número é aquele que apresentar o ‘0’ na diferença dos padrões (sempre percorrendo o número da esquerda para a direita).

Problema com Arredondamento

Consideremos o incômodo problema de representar o número 2,625 no sistema de ponto flutuante de um byte.

Primeiramente, escrevemos 2,625 em binário, obtendo 10.101.

Entretanto, ao copiarmos este código no campo da mantissa, não haverá espaço suficiente, e assim o último 1 (o qual representa a última parcela: 0,125) se perde:

2,625d → 10.101b
Expoente → 110
Mantissa → 10101

Logo temos:

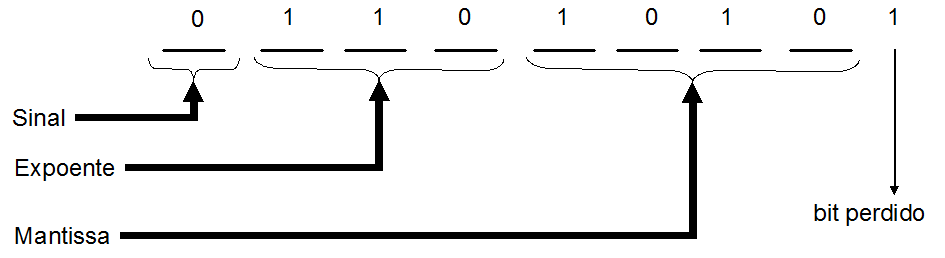
Figura 9 - Problema de arredondamento no sistema de ponto flutuante de um byte.

Ao ignorarmos este problema, e continuarmos a preencher o campo do expoente e do bit do sinal, teremos o padrão de bits 01101010, que representa o valor 2,5 e não 2,625: o fenômeno assim observado é denominado erro de arredondamento, devido o campo da mantissa ter apenas quatro bits, enquanto, por questão de precisão, seriam necessários no mínimo cinco bits.

Normalização na representação

A notação científica, utilizada em ponto flutuante, permite que um mesmo n.º possa ser representado de várias maneiras com os mesmos dígitos.

Exemplo em decimais:

43.789E+12 = .43789E+14 =  43789E+09 ...

A notação de ponto flutuante também pode utilizar o ponto à esquerda do MSB da mantissa ou definir que o ponto seja colocado imediatamente após o primeiro '1' da mantissa.

Quando a notação ponto flutuante cumpre essa norma, por definição, diz-se que um dado n.º fp está normalizado.

Em outras palavras, existe sempre um dígito diferente de 0 à esquerda do ponto decimal.

Num exemplo em decimais (para melhor compreensão), com 7 algarismos na representação de fp (5 para a mantissa e 2 para o expoente), o intervalo de representação dum fp normalizado, seria em valor absoluto: [1.0000E-99, 9.9999E+99] .

Existe aqui um certo desperdício na representação normalizada de fp usando 7 algarismos, pois fica excluído todo o intervalo [0.0001E-99, 1.0000E-99[ .

Para se poder otimizar a utilização dos dígitos na representação de fp, aceitando a representação de valores menores que o menor valor normalizado, mas com o menor valor possível do expoente, se designa esta representação de desnormalizada.

Todas as restantes representações designam-se por não normalizadas.

O bit escondido

Um valor normalizado tem sempre um bit '1', à esquerda do ponto decimal.

Assim, e apenas na representação binária normalizada, esse dígito à esquerda do ponto decimal toma sempre o mesmo valor, e é um desperdício do espaço de memória representá-lo fisicamente.

Ele apenas se torna necessário para efetuar as operações, permanecendo escondido durante a sua representação.

Ganha-se um bit para melhorar a precisão, permitindo passar para 24 o n.º de bits da parte fraccionária (numa representação com 32 bits).

Intervalo e precisão de valores representáveis

Pretende-se sempre, com qualquer codificação, obter o maior intervalo de representação possível e simultaneamente a melhor precisão (relacionada com a distância entre 2 valores consecutivos).

Existindo um n.º limitado de dígitos para a representação de ambos os valores, expoente e mantissa, há que ter consciência das consequências de se aumentar ou diminuir, cada um deles.

O intervalo de valores representáveis depende essencialmente do Expoente, enquanto a precisão vai depender do número de dígitos que for alocado para a parte fraccionária, a Mantissa.

Numa representação em binário, a dimensão mínima que se usa fp (que será sempre um múltiplo da dimensão da palavra de memória) deverá ser pelo menos 32.

Usando 32 bits para representação mínima de fp, torna-se necessário encontrar um valor equilibrado para a parte fracionária e para o expoente.

Esse valor é 8 para o expoente, e pelo menos 23 para a parte fracionária.

Overflow e Underflow

Os projetistas do hardware devem encontrar um compromisso entre a mantissa e o expoente dos números em ponto flutuante. A relação entre mantissa e expoente é expressa do seguinte modo: o aumento do número de bits reservados à mantissa aumenta a precisão do número, enquanto o aumento do número de bits reservados ao expoente aumenta o intervalo de variação dos números representados.

Quando o expoente é muito grande ou muito pequeno para ser armazenado no espaço reservado para ele, ocorrem os fenômenos chamados de overflow e underflow respectivamente. Outro fenômeno é o próprio overflow da mantissa como mostrado acima.

Adição e Subtração em Ponto Flutuante

Para se efetuar qualquer operação aritmética, os 3 campos terão de ser identificados e separados para terem um tratamento distinto na unidade que processa os valores em fp.

Bit de Sinal: ficando mais à esquerda, permite usar o mesmo hardware (que trabalha com valores inteiros) para testar o sinal de um valor em fp;
Bits de Expoente: ficando logo a seguir vai permitir fazer comparações quanto à grandeza relativa entre

valores absolutos em fp, sem necessidade de separar os 3 campos: basta comparar os valores como se se tratassem de valores meramente binários.

A adição e a subtração de ponto flutuante tratam os expoentes junto com o valor dos operandos, logo há a necessidade de equalizar os expoentes e efetuar a operação sobre a mantissa equalizada e o resultado deve ser normalizado para a representação utilizada:

Vamos analisar a seguinte adição em Ponto Flutuante:

01101010 + 01011100 = ?

Processo:

Mantissa 1 = 1010

Expoente = 110 (2 na Notação de Excesso)

Mantissa 2 = 1100

Expoente = 101 (1 na Notação de Excesso)

Equalizando os expoentes, temos:

10.100 + 1.100 -------- 100.000

Normalizando:

Resultado = 1000

Expoente = 111 (3 na Notação de Excesso)

Representação do resultado (01101010 + 01011100) em Ponto Flutuante = 01111000

A norma IEEE 754 para valores em fp

Notação não-normalizada

A representação de valores em fp usando 32 bits e com o formato definido anteriormente permite ainda várias combinações para representar o mesmo valor. Por outro lado, não ficou ainda definido como representar os valores desnormalizados, bem como a representação de valores externos ao intervalo permitido com a notação normalizada.

Assim, as mais diversas representações de ponto flutuante já foram propostas, mas …

⇒ O padrão IEEE 754 atualmente é o mais utilizado:

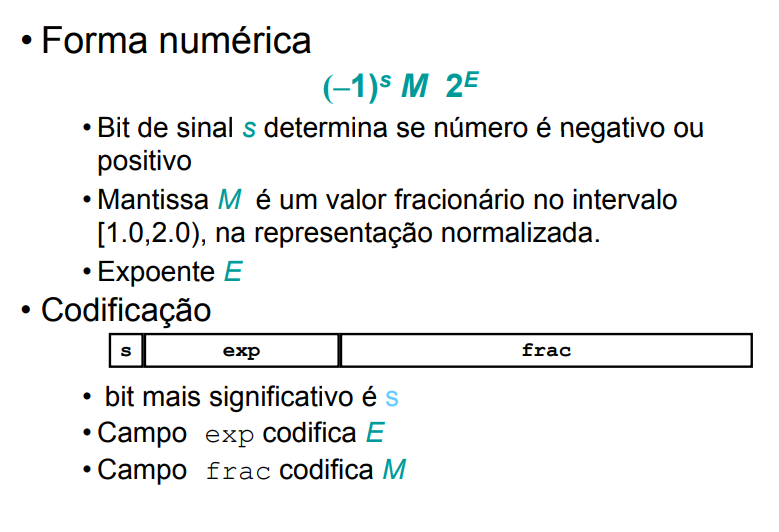
Figura 10 - Notação no padrão IEEE 754.

Criado em 1985 como padrão para representação e aritmética em ponto flutuante
Implementado na grande maioria das CPUs
Define três precisões:
- Single precision (float) - 32 bits ⇒ exp = 8 bits (Excesso 127), frac = 23 bits, s = 1 bit: Faixa de valores: 2^-126 até 2¹²⁷

Figura 11 -(a) Formato e (b) Exemplos de representações de ponto flutuante de 32 bits.

- Double precision (double) - 64 bits ⇒ exp =11 bits (Excesso 1023), frac = 52 bits, s = 1 bit: Faixa de valores: 2^-1022 até 2¹⁰²³
- Double extended precision - 80 bits ⇒ exp =15 bits (Excesso 32.767), frac = 63 bits,s = 1 bit: 2^-16382 até 2¹⁶³⁸³ (1 bit é desperdiçado)

Obs: esta última somente em arquiteturas Intel-like

Aspectos relevantes na norma IEEE 754:

representação do sinal e parte fracionária: segue o formato definido anteriormente, sendo a parte fracionária representada sempre em valor absoluto, e considerando o bit escondido na representação normalizada;
representação do expoente: para permitir a comparação de valores em fp direta, a codificação do expoente é uma notação por excesso, na qual se faz um deslocamento na gama de valores decimais correspondentes ao intervalo de representação de n bits, de 0 a 2^n-1, de modo a que o 0 decimal passe a ser representado não por uma representação binária com tudo a zero, mas por um valor no meio da tabela.

Exemplo: usando 8 bits por exemplo, esta notação permitiria representar o 0 pelo valor 127 ou 128. A norma IEEE adotou o primeiro destes 2 valores, pelo que a representação do expoente se faz por notação por excesso 127. Assim, o expoente varia assim entre -127 e +128;

Notação normalizada

valor decimal de um fp em binário (normalizado):

 V = (-1)^S * (1.M) * 2^(E-127)

, em que S, M e E representam respectivamente os valores em binário dos campos no formato em fp;

representação de valores desnormalizados: para poder contemplar este tipo de situação a norma IEEE reserva o valor de E = 0000 0000b para representar valores desnormalizados, desde que se verifique também que M ≠ 0; o valor decimal vem dado por V = (-1)^S * (0.M)*2^-126
representação do zero: é o caso particular previsto em cima, onde E = 0 e M = 0 ;
representação de ±∞ : a norma IEEE reserva a outra extremidade de representação do expoente; quando E = 1111 1111b e M = 0 , são esses os "valores" que se pretendem representar;
representação de n.º não real: quando o valor que se pretende representar não é um n.º real (imaginário por exemplo), a norma prevê uma forma de o indicar para posterior tratamento por rotinas de exceção; neste caso E = 1111 1111b e M ≠ 0 .

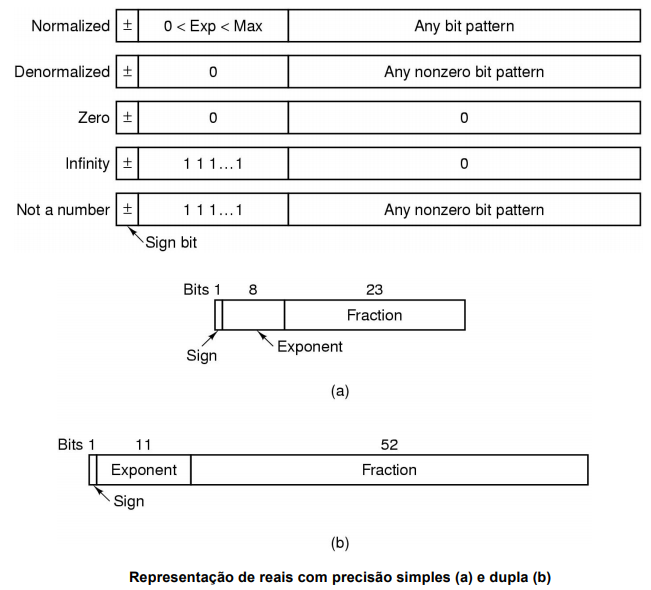
Figura 12 - Representação de reais com precisão simples (a) e dupla (b).

Exemplos:

Figura 13 - Exemplo com representação de reais com precisão simples.

Figura 14 - Exemplo com representação de reais com precisão dupla.

Figura 15 - A aritmética com representação de reais.

Exercícios

1) Converta os valores decimais abaixo para a notação IEEE 754, precisão simples:

a) 158.125d

b) 490.5625d

2) Converta os valores ponto flutuante abaixo, notação IEEE 754 precisão simples, para base decimal:

a) 1110.0001.0110.0000.0000.0000.0000.0000

b) 0010.1000.1001.0101.0000.0000.0000.0000

Solução dos Exercícios Ponto Flutuante

1a) 158,125d = 10011110,001b = 1.0011110001 x 2^7

 Sinal = 0b
 Expoente = 7 + 127 = 134 = 10000110b
 Mantissa = (1,)0011110001b = 00111100010000000000000

Portanto:

 158,125d = 01000011000111100010000000000000b

1b) 490,5625d = 111101010,1001b = 1,111010101001b x 2^8

 Sinal = 0
 Expoente = 8 + 127 = 135 = 10000111b
 Mantissa = (1,)111010101001b = 11101010100100000000000

Portanto:

  490,5625d = 01000011111101010100100000000000b

2a) 1110.0001.0110.0000.0000.0000.0000.0000b

 = 1 11000010 (1,)11000000000000000000000b

Sinal: - Expoente: 11000010b = 194d ⇒ 194 - 127 = 67 Mantissa: 1,1100 = 1,75d

⇒ 1,75 . 2^67 = 1,75 . 147573952589676412928 = 258254417031933722624d

Portanto:

 1110.0001.0110.0000.0000.0000.0000.0000b = -2,75. 2^67 d = -258.254.417.031.933.722.624d

2b) 0010.1000.1001.0101.0000.0000.0000.0000b

  = 0 01010001 (1,)00101010000000000000000

Sinal: + Expoente: 01010001 = 81 ⇒ 81 - 127 = -46 Mantissa: 1,0010101 = 1,1640625

 ⇒ 1,1640625 . 2^-46 = 1,1640625 . 1,4210854715202003717422485351563e-14 = 1,6542323066914832452312111854553e-14

Portanto:

 0010.1000.1001.0101.0000.0000.0000.0000b = 1,6542323066914832452312111854553e-14

Referências

[1] | Cálculo Numérico

MI1022806 2021 1 AULA04

Índice

Sistemas de Numeração

Conversão entre bases

Representação de Inteiros

Base hexadecimal

Números negativos

Sinal e Amplitude

Complemento 1

Complemento 2

Notação em Excesso

Overflow

Representação de Reais

Ponto Flutuante

Problema com Arredondamento

Normalização na representação

O bit escondido

Intervalo e precisão de valores representáveis

Overflow e Underflow

Adição e Subtração em Ponto Flutuante

A norma IEEE 754 para valores em fp

Notação não-normalizada

Notação normalizada

Exercícios

Referências

Menu de navegação

Pesquisa

2¹⁰	2²⁰	2³⁰	2⁴⁰	2⁵⁰	2⁶⁰	2⁷⁰	2⁸⁰	2⁹⁰	2¹⁰⁰
1 kilo	1 Mega	1 Giga	1 Tera	1 Peta	1 Exa	1 Zeta	1 Yota	1 ????	1 ????
~10³	~10⁶	~10⁹	~10¹²	~10¹⁵	~10¹⁸	~10²¹	~10²⁴	~10²⁷	~10^30*

Binário (8 bits)	Sinal + Ampl	Compl p/1	Compl p/2	Excesso (128)
0 0 0 0 0 0 0 1₂	+1	+1	+1	-127
1 0 0 0 0 0 0 1₂	-1	-126	-127	+1
1 1 1 1 1 1 1 0₂	-126	-1	-2	+126

Binário (8 bits)	Sinal + Ampl	Compl p/1	Compl p/2	Excesso (7)	Excesso (8)
0 0 0 0	0	0	0	-7	-8
0 0 0 1	1	1	1	-6	-7
0 0 1 0	2	2	2	-5	-6
0 0 1 1	3	3	3	-4	-5
0 1 0 0	4	4	4	-3	-4
0 1 0 1	5	5	5	-2	-3
0 1 1 0	6	6	6	-1	-2
0 1 1 1	7	7	7	0	-1
1 0 0 0	-0	-7	-8	1	0
1 0 0 1	-1	-6	-7	2	1
1 0 1 0	-2	-5	-6	3	2
1 0 1 1	-3	-4	-5	4	3
1 1 0 0	-4	-3	-4	5	4
1 1 0 1	-5	-2	-3	6	5
1 1 1 0	-6	-1	-2	7	6
1 1 1 1	-7	-0	-1	8	7