LFSR em VHDL
A implementação de um contador LFSR (Linear Feedback Shift Register) em VHDL pode ser feita usando como base o código 9.10 do livro de Pong Chu.
1 Código original P. Chu
O código funciona para um contador de 4 bits, e está descrito em 2 segmentos. O primeiro segmento faz a atualização do registrador de estado, e o segundo segmente determina o próximo estado do contador, através da realimentação:
architecture shift_right_LFSR of lfsr4 is
signal r_reg, r_next: std_logic_vector(3 downto 0);
signal fb: std_logic;
constant SEED: std_logic_vector(3 downto 0):="0001";
begin
-- atualização do registrador de estado
process(clk,reset)
begin
if (reset='1') then
r_reg <= SEED;
elsif (clk'event and clk='1') then
r_reg <= r_next;
end if;
end process;
-- lógica de próximo estado
fb <= r_reg(1) xor r_reg(0);
r_next <= fb & r_reg(3 downto 1);
-- lógica de saída
q <= r_reg;
end architecture;
Para implementar um contador LFSR com outra quantidade de bits, é necessário conhecer o polinomio gerador. Existem tabelas para diferentes números de bits em:
- LFSR na wikipedia, seção Example polynomials for maximal LFSRs.
- Note que para 4 bits a tabela indica o uso dos dois bits mais a esquerda. Taps = 1100, ou Taps (hex) = 0xC. Esses tabs indicariam quais os bits devem ser entrada da porta XOR. No caso seriam os bits 3 e 2. No entanto no código do P.Chu, por ser a rotação dos bits para a direita (shift right), os bits a serem utilizados seriam o 0 e 1.
- Para obter outros taps para outros LFSRs, pode-se consultar o arquivo [1], que contém um número muito grande de opções.
2 Código modificado
Fazendo uma pequena modificação na lógica de próximo estado, rotacionando os bits para a esquerda (shift left), é possível obter um LFSR sem essa conversão.
-- para o tap 0xC ou 1100
fb <= r_reg(3) xor r_reg(2);
r_next <= r_reg(2 downto 0) & fb;
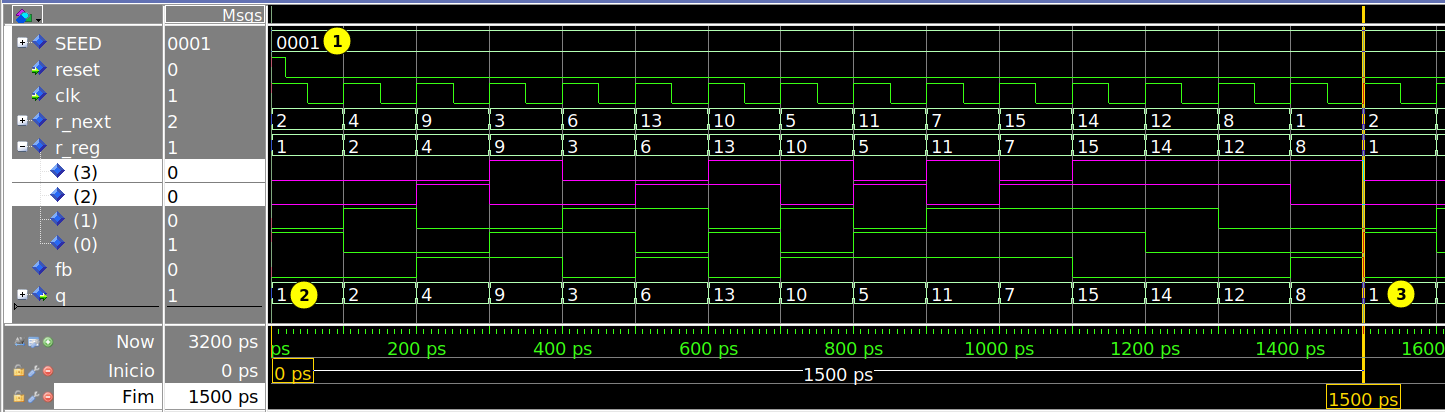
A seguir a simulação feita no Modelsim do LFSR modificado. Note que o valor inicial da saída (2) é dado pela constante SEED (1). A partir desse valor são gerados sucessivos números, até iniciar um novo ciclo depois de 15 valores (3). A lógica de geração do próximo número no LFSR é simples, e envolve apenas uma operação de XOR entre os bits anteriores, no caso o bit 3 e o bit 2, destacados em magenta.
Figura 1 - Simulação do LFSR de 4 bits tab (0xC) shift left
3 LFSR com 10 bits
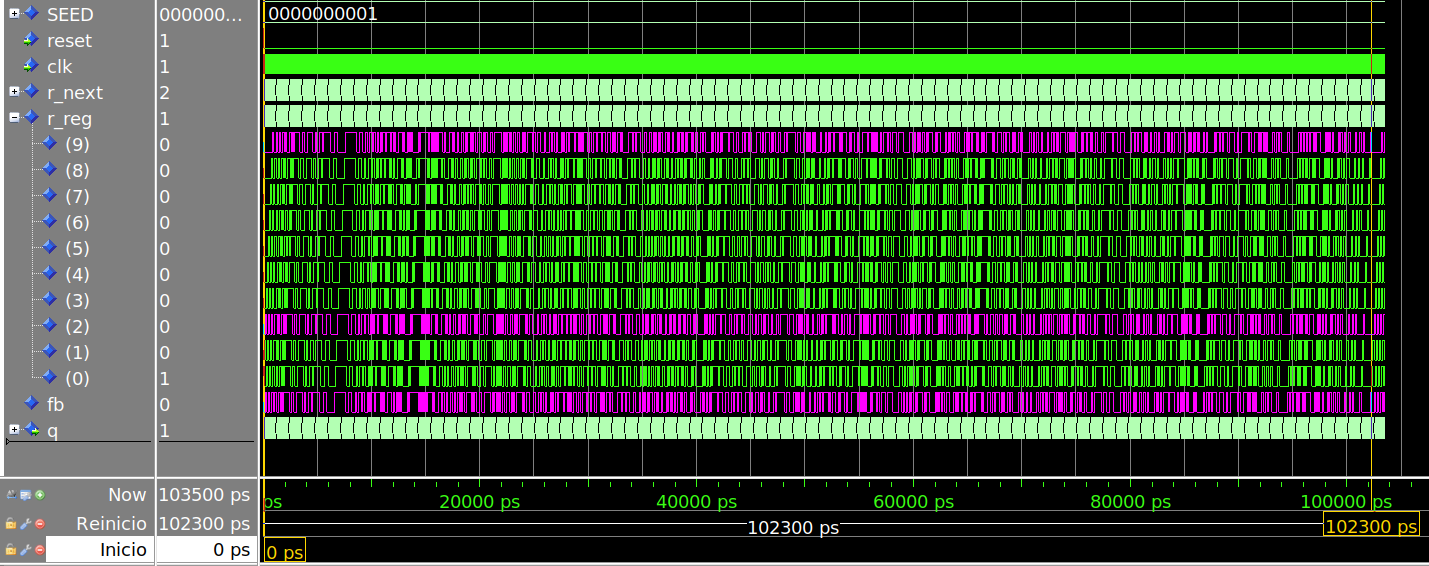
Nas figuras abaixo é ilustrado o funcionamento de um contador LFSR de 10 bits. Na Figura 2, é mostrada a contagem inicial 1, 2, 4, 9, 18, 36, 73, 146, ... Depois de 1023 valores diferentes, o ciclo recomeça na Figura 3 após o 512, 1, 2, 4, 9, 18, 36, 73, 146, ...
Figura 2 - Simulação do LFSR de 10 bits tab (0x204) shift left (início)
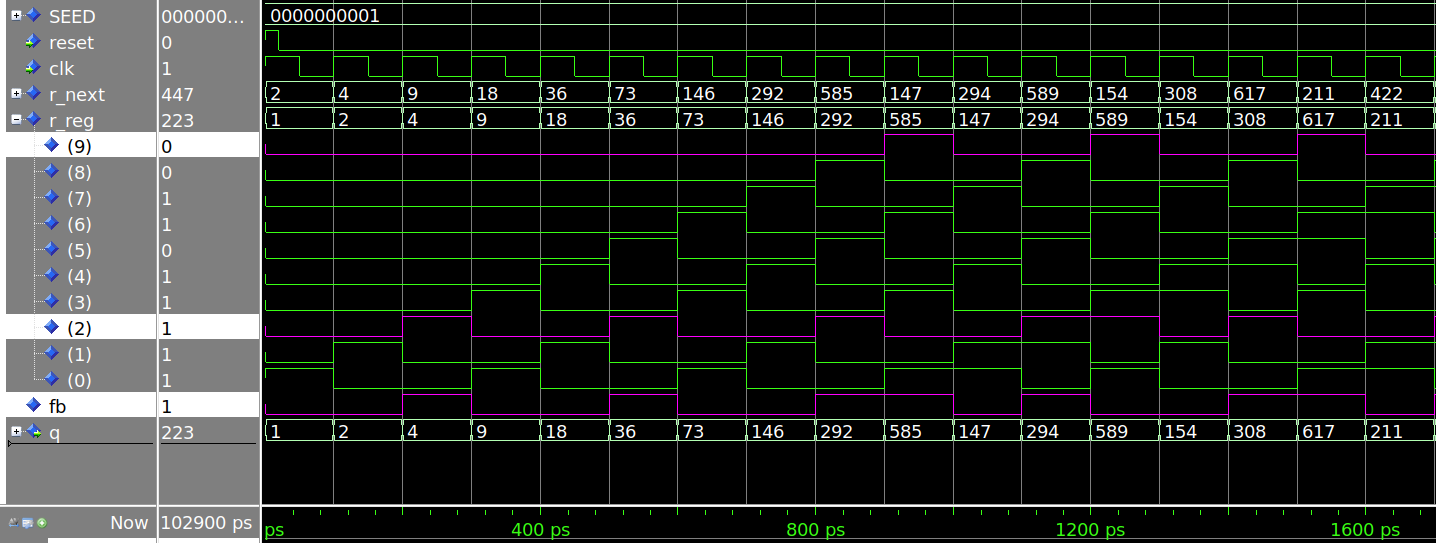
Figura 3 - Simulação do LFSR de 10 bits tab (0x204) shift left (reinício)
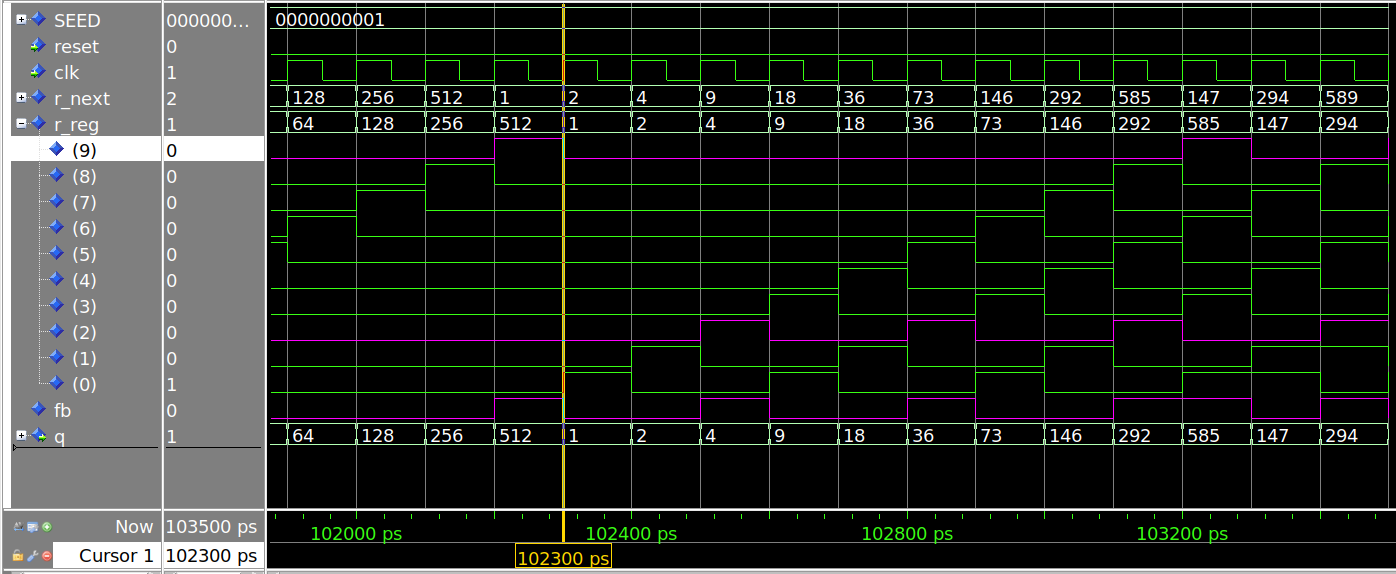
Figura 4 - Simulação do LFSR de 10 bits tab (0x204) shift left (ciclo completo)