GAL-EngTel (Plano de Ensino)

|
MINISTÉRIO DA EDUCAÇÃO |
Plano de Ensino
- Dados gerais
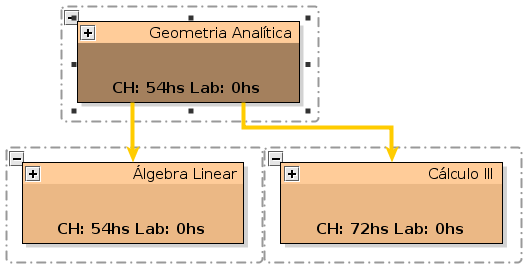
- COMPONENTE CURRICULAR: GAL - GEOMETRIA ANALÍTICA
- CARGA HORÁRIA: 3 HORAS/SEMANA 54 HORAS. TEÓRICA = 54 HORAS. LABORATÓRIO = 0 HORAS
- Objetivos
- Instrumentalizar o aluno para a aplicação dos conceitos matemáticos nas disciplinas subsequentes do curso de Engenharia de Telecomunicações-IFSC/São José;
- Familiarizar-se com a escrita matemática formal;
- Desenvolver a capacidade de raciocínio abstrato (lógico-matemático) como um todo;
- Abordar os conceitos geométricos superior visando introduzir os conceitos de vetor no plano e espaço, plano coordenado, base, cônicas e quádricas;
- Utilizar conceitos geométricos para introduzir conceitos algébricos;
- Demonstrar e aprofundar na algebrização de noções geométricas;
- Promover a utilização dos conceitos em aplicações simples;
- Iniciar o aprendizado de conceitos relativos à Matemática superior;
- Estabelecer relações com os conceitos matemáticos já apreendidos no ensino básico.
- Ementa
- Vetores. Vetores no plano e no espaço. Produto de vetores. Estudo da reta e do plano. Distâncias. Cônicas. Superfícies.
- Conteúdo Programático
- 1. Vetores: tratamento geométrico, noção intuitiva, casos particulares, operações: Vetores no plano; Vetores no espaço (4h).
- 2.Produto escalar, vetorial e misto (6h).
- 3.A reta: Equação vetorial, paramétrica, simétrica e reduzida; Ângulo de duas retas; Condição de paralelismo, ortogonalidade e coplanaridade de duas retas; Posições relativas entre duas retas; Intersecção de duas retas (8h).
- 4.O plano: Equação geral e paramétrica; Casos particulares; Ângulo: entre dois planos e de uma reta com um plano; Intersecção: entre dois planos e de uma reta com plano (12h).
- 5. Distâncias: Entre dois pontos; De um ponto a uma reta; Entre duas retas; De um ponto a um plano; Entre dois planos; De uma reta a um plano (8h).
- 6.Cônicas: Parábola; Elipse; Hipérbole; Seções cônicas (6h).
- 7.Superfícies quadráticas (6h).
- Avaliações (4h).
- Estratégias de ensino utilizadas
- Aulas expositivas e dialogadas com o uso de lousa, giz, projetor multimídia, resolução de exercícios e utilização do software matemático geogebra.
| Avaliação | ||||
|---|---|---|---|---|
|
Segunda chamada Para poder fazer cada recuperação, de acordo com o Art. 52 do Regimento Didático Pedagógico (RDP),
"o aluno terá nova oportunidade de prestar atividades de avaliação não realizadas por motivo de doença ou por falecimento de familiares até 2º grau, convocação do judiciário e do serviço militar, desde que: i. comunique em até 5 (cinco) dias letivos, contados do início do afastamento o motivo do impedimento à secretaria do departamento de ensino, pesquisa e extensão do campus; ii. encaminhe em até 2 (dois) dias letivos contados do final do afastamento, um requerimento à coordenadoria de curso, com os documentos comprobatórios do impedimento. § 1º o requerimento deverá indicar a data e horário da avaliação não realizada, o componente curricular e o nome do seu professor. § 2º para comprovação de ausência por motivo de saúde, somente será aceito o atestado médico."
1 Bibliografia do PPCv2015-2
- Bibliografia Básica
- GENESIO LIMA DOS REIS Geometria analítica; 2ª ed. Rio de Janeiro:LTC, 2002. p. ISBN 9788521610656. Qtdade Na Biblioteca para a Disciplina:6
- Paulo Boulos Geometria Analítica - Um tratamento vetorial; 1ª ed. São Paulo:Prentice Hall Brasil, 2005. p. ISBN 9788587918918. Qtdade Na Biblioteca para a Disciplina:6
- Paulo Winterle Vetores e geometria analítica; 1ª ed. São Paulo:Makron, 2000. p. ISBN 9788534611091. Qtdade Na Biblioteca para a Disciplina:6
- Bibliografia Complementar
- VENTURI, JACIR J. Álgebra Vetorial e Geometria Analítica; 9ª ed. Curitiba:AUTORES PARANAENSES, 2009. p. ISBN . "Disponível em: http://www.geometriaanalitica.com.br/livros/av.pdf"
- LINDQUIST, Mary Montgomery; SHULTE, Albert P. Aprendendo e ensinando geometria; ed. São Paulo:Atual, 1998. 308p. ISBN 857056595x. Qtdade Na Biblioteca para a Disciplina:2
- VENTURI, JACIR J. Cônicas e Quádricas; 5ª ed. Curitiba:AUTORES PARANAENSES, 2003. p. ISBN . "Disponível em: http://www.geometriaanalitica.com.br/livros/cq.pdf"
- BALDIN YURIKO YAMAMOTO GEOMETRIA ANALÍTICA PARA TODOS E ATIVIDADES COM OCTAVE E GEOGEBRA; 1ª ed. [S.l]:EDUFSCAR, 2012. p. ISBN 9788576002499. Qtdade Na Biblioteca para a Disciplina:2
- Dorial A. MELLO Vetores e uma iniciação à Geometria Analítica; 2ª ed. São Paulo:Livraria da Física, 2012. p. ISBN 9788578611071. Qtdade Na Biblioteca para a Disciplina:2
2 Bibliografia Inicialmente Sugerida
- Bibliografia Básica
- Bibliografia Básica
- Paulo Winterle Vetores e geometria analítica; 1ª ed. São Paulo:Makron, 2000. p. ISBN 9788534611091
- GENESIO LIMA DOS REIS Geometria analítica; 2ª ed. Rio de Janeiro:LTC, 2002. p. ISBN 9788521610656
- Paulo Boulos Geometria Analítica - Um tratamento vetorial; 1ª ed. São Paulo:Prentice Hall Brasil, 2005. p. ISBN 9788587918918
- Bibliografia Complementar
- BALDIN YURIKO YAMAMOTO GEOMETRIA ANALÍTICA PARA TODOS E ATIVIDADES COM OCTAVE E GEOGEBRA; 1ª ed. [S.l]:EDUFSCAR, 2012. p. ISBN 9788576002499
- VENTURI, JACIR J. Cônicas e Quádricas; 5ª ed. Curitiba:AUTORES PARANAENSES, 2003. p. ISBN Disponível em http://www.geometriaanalitica.com.br/livros/cq.pdf
- VENTURI, JACIR J. Álgebra Vetorial e Geometria Analítica; 9ª ed. Curitiba:AUTORES PARANAENSES, 2009. p. ISBN Disponível em http://www.geometriaanalitica.com.br/livros/av.pdf
- Dorial A. MELLO Vetores e uma iniciação à Geometria Analítica; 2ª ed. São Paulo:Livraria da Física, 2012. p. ISBN 9788578611071
3 ANEXOS
- Cronograma de atividades
- Horário de Aula e Atendimento Paralelo
- Projeto Ensino e Aprendizagem de Matemática com Vídeos