EDI18701 2016 2 AULA04

Circuitos Combinacionais

Os circuitos lógicos em sistemas digitais podem ser divididos em dois tipos: circuitos combinacionais, visto nessa unidade curricular, e circuitos sequenciais vistos no módulo 2.

Um circuito combinacional é constituído por um conjunto de portas lógicas as quais determinam os valores das saídas diretamente a partir dos valores atuais das entradas. Pode-se dizer que um circuito combinacional realiza uma operação de processamento de informação a qual pode ser especificada por meio de um conjunto de equações Booleanas. No caso, cada combinação de valores de entrada pode ser vista como uma informação diferente e cada conjunto de valores de saída representa o resultado da operação. A Figura 1 mostra o diagrama de blocos genérico de um circuito combinacional.

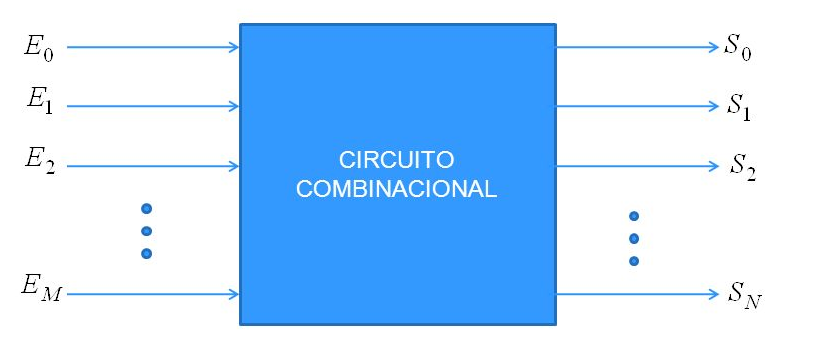
Figura 1 - Esquema geral de um circuito combinacional.

O objetivo da análise de um circuito combinacional é determinar seu comportamento. Então, dado o diagrama de um circuito, deseja-se encontrar as equações que descrevem suas saídas. Uma vez encontradas tais equações, pode-se obter a tabela verdade, caso esta seja necessária. É importante certificar-se que o circuito é combinacional e não sequencial.

O procedimento básico para se determinarem as equações que descrevem as saídas de um circuito combinacional é o seguinte:

Passo 1

É preciso dar um nome para as variáveis associadas a cada saída de cada porta do circuito,

exceto aquelas saídas que já possuem nome (como por exemplo, as saídas do circuito);

Passo 2

Depois, a partir da esquerda, e seguindo a ordem de precedência determinada pelas ligações, determinar as equações associadas a cada variável, até que as equações de todas as saídas tenham sido encontradas.

Uma vez determinadas as equações das saídas, a montagem da tabela verdade será direta, havendo uma coluna para cada saída.

Exemplo

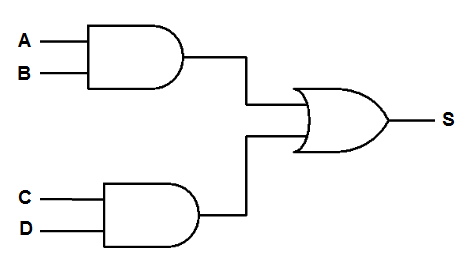
Determinar a equação da saída S do circuito abaixo, bem como sua tabela verdade.

Equação Booleana

$S=(A.B)+(C.D)\,$

Tabela verdade

ABCD	A.B	C.D	S=(A.B)+(C.D)
0000	0	0	0
0010	0	0	0
0011	0	1	1
0100	0	0	0
0101	0	0	0
0110	0	0	0
0111	0	1	1
1000	0	0	0
1001	0	0	0
1010	0	0	0
1011	0	1	1
1100	1	0	1
1101	1	0	1
1110	1	0	1
1111	1	1	1

Observa-se que a saída S é a soma da multiplicação entre A.B e C.D. Logo, sempre que os pares A.B e/ou C.D forem iguais a 1, a saída vai ser 1.

Circuitos Aritméticos

Um circuito combinacional aritmético implementa operações aritméticas como adição, subtração, multiplicação e divisão com números binários. A operação aritmética mais simples é a adição de dois dígitos binários, que consiste de quatro possíveis operações elementares: 0+0=0, 0+1=1, 1+0=1 e 1+1=10. As três primeiras operações produzem um dígito de soma. Entretanto, quando ambos os operandos são iguais a 1, são necessários dois dígitos para expressar seu resultado. Neste caso, o transporte (vai-um ou carry) é somado ao próximo par mais significativo de bits. Um circuito combinacional que implementa a adição de dois bits é chamado meio-somador (half adder). Um circuito que implementa a adição de três bits (dois bits significativos e um carry) é chamado de somador completo (full adder). Estes nomes decorrem do fato de que com dois meio-somadores pode-se implementar um somador completo. O somador completo é um circuito aritmético básico a partir do qual todos os outros circuitos aritméticos são construídos.

Meio somador (half adder)

A operação aritmética mais simples é a adição de dois dígitos binários (bits), a qual pode ser vista como a adição de dois números binários de um bit cada. Considerando-se todas as 4 combinações de valores que podem ocorrer, os resultados possíveis dessa adição são:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Repare que no último caso acima, o resultado da adição é o valor 2, que em binário necessita de dois dígitos para ser representado (10). Ora, um circuito aritmético para realizar a adição de dois bits deve operar corretamente para qualquer combinação de valores de entrada. Isso significa que o circuito para a adição de dois bits deve possuir duas entradas e duas saídas, conforme ilustrado na Figura 2.

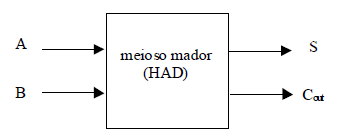
Figura 2 - Esquema de entradas e saídas de um meio somador.

Denomina-se meia-soma a operação de adição de dois bits. O circuito mostrado na Figura 2 é denominado meio somador (half adder). As duas entradas, A e B, representam os dois bits a serem adicionados. A saída S representa o dígito menos significativo do resultado, enquanto que a saída C_out representa o dígito mais significativo do resultado, o qual também é conhecido por transporte de saída (carry out), uma vez que ele assume valor 1 somente quando o resultado da soma de A e B não pode ser representado num único dígito. A fim de se projetar o circuito do meio somador, devemos montar uma tabela verdade para as saídas S e C_out utilizando-se os valores que resultam da adição de dois dígitos binários, como segue:

A	B	Cout	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Note que a saída S nada mais é do que o XOR entre A e B (S = A .B + A.B = A (+) B). Já a saída C_out é o AND entre A e B (C_out = A.B). Então, um circuito para o meio somador usa apenas uma porta XOR e uma porta AND ambas de duas entradas, conforme mostrado na Figura 3.

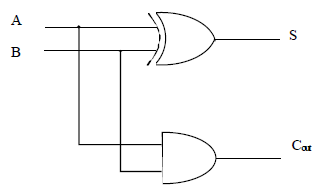
Figura 3 - Circuito para o meio somador.

Somador completo (full adder)

Ao somarmos dois números binários que possuem mais de um dígito cada ocorrer transporte diferente de zero para a soma de um par de dígitos intermediários, a soma do par seguinte deverá considerar esse transporte proveniente do par anterior, conforme ilustra o exemplo a seguir.

C: 1 1 0 1
     1 1 0 1
+    1 1 0 1
------------
   1 1 0 1 0

O exemplo mostrado acima ilustra bem o fato de, para cada posição exceto a menos significativa, o resultado é obtido mediante a adição de três bits: um pertencente ao número A, um pertencente ao número B e um terceiro que é o transporte proveniente do resultado da adição entre os bits da posição anterior. O circuito capaz de realizar a soma de três bits (A, B e C_in), gerando o resultado em dois bits (S e C_out) é denominado somador completo (full adder). Apesar da entrada C_in normalmente receber o transporte proveniente da soma imediatamente anterior (carry in), a rigor as três entradas são absolutamente equivalentes sob o ponto de vista funcional. A tabela verdade para a soma completa é mostrada a seguir, e Figura 4 mostra um circuito para o somador completo.

A	B	Cin	Cout	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

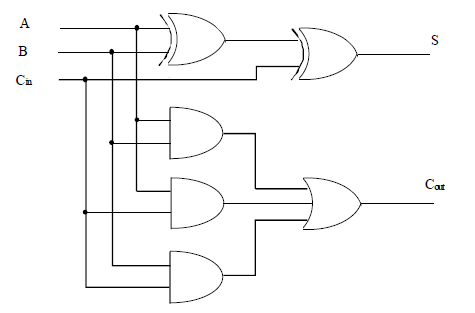
Figura 4 - Circuito para o somador completo.

Exercícios

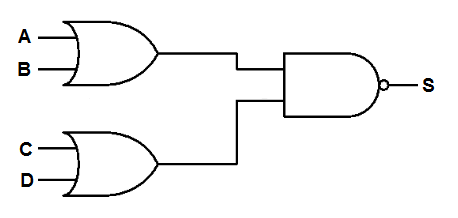
1) Determinar a equação da saída S do circuito abaixo, bem como sua tabela verdade.

Equação Booleana

$S=...\,$

Tabela verdade

ABCD	A+B	C+D	S
0000
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

---

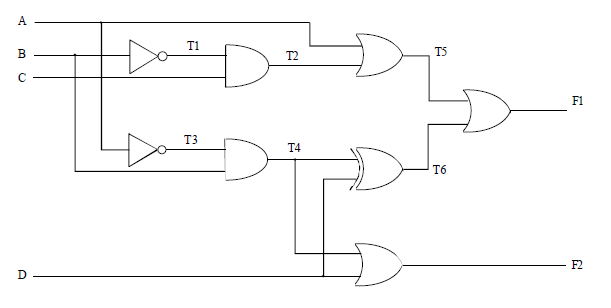
2) Determinar as equações das saídas F1 e F2 do circuito que segue.

É importante perceber que já existe as variáveis associadas às saídas das portas de T1, T2, T3...
Há somente duas portas cujas saídas já tem nome, que são justamente as saídas do circuito: F1 e F2.

Referências

[1] http://www.inf.ufsc.br/~guntzel/isd/isd3.pdf

---

<<	<>	>>