Conectando uma fonte, condições de contorno
1 Conectando uma Fonte
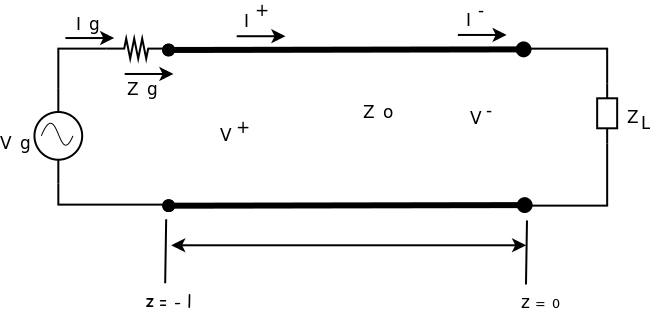
Podemos considerar uma linha de transmissão como o elemento que liga uma fonte de tensão ou corrente (gerador, transmissor, antena, ...) à uma carga (impedância, receptor, antena, ...). Quando analisamos o terminal "final" da linha, modelamos a carga por seu impedância de entrada. Não precisamos de mais informações da carga para analisar a tensão e a corrente na linha.
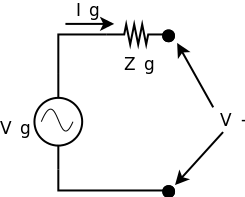
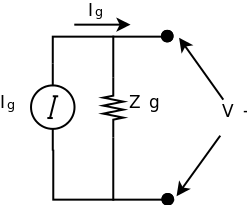
Em relação a fonte, para análise da linha de transmissão, modelamos a mesma pelo seu circuito equivalente de Thevenin ou Norton.
figura 1: circuitos de Thevenin e Norton
Utilizando Thevenin o circuito completo da linha com fonte e carga passa a ser:
Do circuito completo obtemos as relações:
- (1)
- (2)
de (1) temos:
- (3)
lembrando que podemos substituir na equação (3):
- (4)
como:
podemos escrever Z_{in} como:
- (5)
substituindo (4) e (5) em (2):
| (6) |
A equação (6) mostra a relação de com a fonte ( e ), com a linha (Z e l) e com a carga, pois é dependente de . Neste equacionamento também é indicado que a tensão incidente da linha depende da fonte e da carga!
Como também depende de , as duas ondas de tensão, incidente e refletida, são dependentes da fonte e da carga. Isto é, somente conhecendo as condições de contorno (fonte e carga) é que podemos definir e .