Coeficiente de reflexão, Impedância de entrada e Potência

1 Coeficiente de reflexão

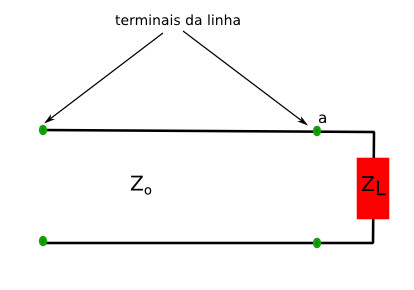
Uma linha de transmissão possui uma impedância característica Zo definida pela relação entre a $V^{+}$ e $I^{+}$. Considere que uma carga $Z_L$ é acoplada a um dos terminais da linha (figura 1).

figura 1: Linha com carga

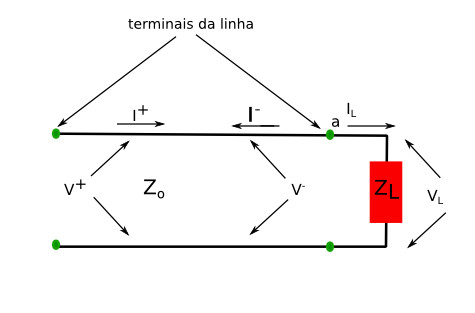
Sobre essa carga teremos uma tensão $V_L$, fazendo circular uma corrente $I_L$. Na linha teremos as tensões $V^{+}$ e $V^{-}$ e as correntes $I^{+}$ e $I^{-}$, conforme indicado no figura 2.

figura 2: Linha com carga com tensões e correntes.

Podemos escrever $Z_L$ como:

$Z_L=\frac{V_L}{I_L}$

Mas no nó terminal a da linha a tensão é a soma fasorial de $V^{+}$ e $V^{-}$, portanto:

$V_L=V_o^{+}{e}^{-\gamma z}+V_o^{-}{e}^{\gamma z}$

Do terminal a podemos retirar ainda a relação:

$I_L=I_o^{+}{e}^{-\gamma z}+I_o^{-}{e}^{\gamma z}$

Considerando o terminal a como o ponto onde z = 0:

$Z_L=\frac{V_o^{+}+V_o^{-}}{I_o^{+}+I_o^{-}}$

como em z= 0,

$Z_o=\frac{V_o^{+}}{I_o^{+}}=\frac{-V_o^{-}}{I_o^{-}}$

podemos escrever:

$Z_L=\frac{V_o^{+}+V_o^{-}}{\frac{V_o^{+}}{Z_o}-\frac{V_o^{-}}{Z_o}}$

fazendo algumas manipulações algébricas:

$\frac{V_o^{-}}{V_o^{+}}=\frac{Z_L-Z_o}{Z_L+Z_o}$

À relação $\frac{V^{-}}{V^{+}}$ chamamos de coeficiente de reflexão e representamos pela letra grega Γ

Para diferenciar o coeficiente de reflexão na carga do obtido em outro ponto da linha iremos identificar esse por ${\mathrm{\Gamma }}_L$

${\mathrm{\Gamma }}_L=\frac{Z_L-Z_o}{Z_L+Z_o}$

2 coeficiente de reflexão afastado da carga

O valor de Γ em qualquer ponto da linha será dado pela relação entre $\frac{V^{+}}{V^{-}}$, sendo assim para um ponto afastado uma distância $l$ da carga teremos:

${\mathrm{\Gamma }}_{in}=\mathrm{\Gamma }(z)=\frac{V_o^{-}{e}^{\gamma z}}{V_o^{+}{e}^{-\gamma z}}={\mathrm{\Gamma }}_L{e}^{2\gamma z}$

considerando um deslocamento $l$ a partir da carga (z=0) para a esquerda (sentido -z) temos:

${\mathrm{\Gamma }}_{in}={\mathrm{\Gamma }}_L{e}^{-2\gamma l}(1)$

3 Impedância de entrada

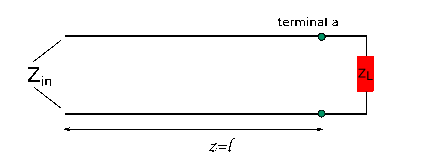
A relação entre a tensão e a corrente total em um determinado ponto da linha de transmissão é conhecida como Zin, impedância de entrada.

figura 3: Impedância de entrada - é a impedância vista em um ponto da linha.

Observe que $Z_{i}n$ é dada em função de $-l$

não estamos nos referindo a Zo (impedância característica) esta corresponde a relação $\frac{V^{+}}{I^{+}}$, enquanto que Zin é dada por:

$Z_{in(-l)}=\frac{V_o^{+}{e}^{\gamma l}+V_o^{-}{e}^{-\gamma l}}{I_o^{+}{e}^{\gamma l}+I_o^{-}{e}^{-\gamma l}}$

substituindo $I_o^{+}$ e $I_o^{-}$ por:

$I_o^{+}=\frac{V_o^{+}}{Z_o}$

$I_o^{-}=\frac{-V_o^{-}}{Z_o}$

temos:

$Z_{in(z)}=Z_o\frac{V_o^{+}{e}^{\gamma z}+V_o^{-}{e}^{-\gamma z}}{V_o^{+}{e}^{\gamma z}-V_o^{-}{e}^{-\gamma z}}$

agora substituindo $V_o^{-}={\mathrm{\Gamma }}_L{V}_o^{+}$:

$Z_{in(z)}=Z_o\frac{V_o^{+}{e}^{\gamma z}+{\mathrm{\Gamma }}_L{V}_o^{+}{e}^{-\gamma z}}{V_o^{+}{e}^{\gamma z}-{\mathrm{\Gamma }}_L{V}_o^{+}{e}^{-\gamma z}}$

$Z_{in(z)}=Z_o\frac{e^{\gamma z}+{\mathrm{\Gamma }}_L{e}^{-\gamma z}}{e^{\gamma z}-{\mathrm{\Gamma }}_L{e}^{-\gamma z}}$

$Z_{in(z)}=Z_o\frac{e^{\gamma z}+\frac{(Z_L-Z_o)}{(Z_L+Z_o)}{e}^{-\gamma z}}{e^{\gamma z}-\frac{(Z_L-Z_o)}{(Z_L+Z_o)}{e}^{-\gamma z}}$

$Z_{in(z)}=Z_o\frac{Z_L(e^{\gamma z}+e^{-\gamma z})+Z_o(e^{\gamma z}-e^{-\gamma z})}{Z_L(e^{\gamma z}-e^{-\gamma z})+Z_o(e^{\gamma z}+e^{-\gamma z})}$

dividindo numerador e denominador por $e^{\gamma z}+e^{-\gamma z}$ e lembrando que:

$\tanh x=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

temos:

$Z_{in(z)}=Z_o\frac{Z_L+Z_{o}tanh\gamma z}{Z_o+Z_{L}tanh\gamma z}(2)$

4 Potência incidente, entregue à carga e refletida

4.1 Potência incidente

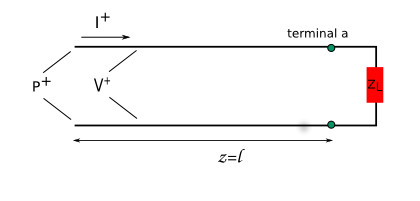
Ao conectar uma fonte em uma linha de transmissão, passa a se propagar pela linha uma onda de tensão e outra de corrente. Essas duas ondas transportam energia elétrica (figura 1).

Figura 4: linha percorrida por onda de tensão e corrente que transmitem potência elétrica.

‎

Se a fonte de tensão for harmônica, cossenoidal por exemplo, podemos calcular a potência média ativa transmitida por:

$P^{+}(l)=\frac{1}{2}\mathrm{\Re }\{V(l{)}^{+}.I(l{)}^{+*}\}$ (3)

$V(l{)}^{+}$ e $I(l{)}^{+}$ são dados por:

$V(l{)}^{+}=V_o^{+}{e}^{-\alpha l}{e}^{-j\beta l}$ (4)

$I(l{)}^{+}=I_o^{+}{e}^{-\alpha l}{e}^{j\theta }{e}^{-j\beta l}$ (5)

O termo $e^{j\theta }$ na equação (5) corresponde ao ângulo de defasagem entre a tensão e a corrente na linha.

Substituindo (4) e (5) em (3) e lembrando que $|Z_o|=\frac{V(z{)}^{+}}{I(z{)}^{+}}$:

$P^{+}(l)=\frac{1}{2}\mathrm{\Re }\{V_o^{+}{e}^{-\alpha l}{e}^{-j\beta l}.I_o^{+}{e}^{-\alpha l}{e}^{-j\theta }{e}^{j\beta l}\}$

$P^{+}(l)=\frac{1}{2}\mathrm{\Re }\{V_o^{+}{e}^{-\alpha l}{e}^{-j\beta l}.\frac{V_o^{+}}{Z_o}{e}^{-\alpha l}{e}^{-j\theta }{e}^{j\beta l}\}$

$P^{+}(l)=\frac{1}{2}\mathrm{\Re }\{\frac{V_o^{+2}}{|Zo|}{e}^{-2\alpha l}{e}^{-j\theta }\}$

o que pode ser escrito como:

$P^{+}(z)=\frac{1}{2}\frac{V_o^{+2}}{|Z_o|}{e}^{-2\alpha l}\cos \theta$ (7)

A equação (7) representa a potência transmitida na linha ou potência incidente. Note que a constante α representa a constante de atenuação da linha.

4.2 Potência entregue à carga

A potência ativa entregue à carga pela linha ($P_L$) pode ser calculada por:

$P_L=\mathrm{\Re }\{V_L.I_L^{*}\}$

Que pode ser reescrita em função das tensões e correntes no terminal a da linha de transmissão.

$P_L=\mathrm{\Re }\{V(z).I(z{)}^{*}\}$

$P_L=\mathrm{\Re }\{(V_o^{+}{e}^{-\alpha z}{e}^{-j\beta z}+V_o^{-}{e}^{\alpha z}{e}^{j\beta z}).(I_o^{+}{e}^{-\alpha z}{e}^{j\theta }{e}^{j\beta z}+I_o^{-}{e}^{\alpha z}{e}^{j\theta }{e}^{-j\beta z})\}$

$P_L=\mathrm{\Re }\{(V_o^{+}{e}^{-\alpha z}{e}^{-j\beta z}+\mathrm{\Gamma }{V}_o^{+}{e}^{\alpha z}{e}^{j\beta z}).(\frac{V_o^{+}}{Z_o}{e}^{-\alpha z}{e}^{j\theta }{e}^{j\beta z}+-\mathrm{\Gamma }\frac{V_o^{+}}{Z_o}{e}^{\alpha z}{e}^{j\theta }{e}^{-j\beta z})\}$

Considerando o terminal a como o ponto onde z=0:

$P_L=\mathrm{\Re }\{(V_o^{+}+\mathrm{\Gamma }{V}_o^{+}).(\frac{V_o^{+}}{Z_o}{e}^{j\theta }-\mathrm{\Gamma }\frac{V_o^{+}}{Z_o}{e}^{j\theta })\}$

$P_L=\mathrm{\Re }\{\frac{V_o^{+2}}{Z_o}{e}^{j\theta }-{\mathrm{\Gamma }}^2\frac{V_o^{+2}}{Z_o}{e}^{j\theta }\}$

$P_L=\mathrm{\Re }\{\frac{V_o^{+2}}{Z_o}{e}^{j\theta }(1-{\mathrm{\Gamma }}^2)\}$

o termo $\mathrm{\Re }\{\frac{V_o^{+2}}{Z_o}{e}^{j\theta }\}$ é exatamente a potência incidente no terminal a portanto:

$P_L=P^{{+}^{\prime }}(1-{\mathrm{\Gamma }}^2)$ (8)

A linha em $P^{{+}^{\prime }}$ na equação (8) representa que o cálculo de $P_L$ deve ser realizado descontando a atenuação da linha, isto é utilizando o valor de $P(z{)}^{+}$ no terminal a.

4.3 Potência Refletida

Manipulando um pouco a equação (8) podemos encontrar o relação entre a potência incidente, a potência refletida e a potência entregue à carga:

$P_L=P^{{+}^{\prime }}(1-{\mathrm{\Gamma }}^2)$

$P_L=P^{{+}^{\prime }}-{\mathrm{\Gamma }}^2{P}^{{+}^{\prime }}$

$P_L=\frac{V^{{+}^{\prime }2}}{Z_o}-{\mathrm{\Gamma }}^2\frac{V^{{+}^{\prime }2}}{Z_o}$

$P_L=\frac{V^{{+}^{\prime }2}}{Z_o}-\frac{(\mathrm{\Gamma }.V^{{+}^{\prime }}{)}^2}{Z_o}$

$P_L=\frac{V^{{+}^{\prime }2}}{Z_o}-\frac{V_o^{{-}^{\prime }2}}{Z_o}$ (9)

O primeiro termo do lado direito da equação (9) corresponde a potência incidente no terminal a e o segundo termo a potência refletida no mesmo terminal. Esta relação mostra que a parcela de potência que chega ao final da linha e não é absorvida pela carga, retorno para linha. Isto é,$V^{-}(z)$ e $I^{-}(z)$ são as ondas refletidas na linha e transportam a potência refletida.

4.3.1 Potências na linha e entregue à carga

Potência incidente	$P^{+}(l)=\frac{V^{{+}^{\prime }2}}{Z_o}{e}^{-2\gamma l}cos\theta$
Potência refletida	$P^{-}(l)=\frac{V^{{-}^{\prime }2}}{Z_o}{e}^{-2\gamma l}cos\theta$
Potência entregue à carga	$P_L=\frac{V^{{+}^{\prime }2}}{Z_o}-\frac{V_o^{-2}}{Z_o}$