CEL18702 AULA06

1 Técnicas Utilizadas na Análise de Circuitos

1.1 Análise de Nós

1.1.1 Dois nós

Tomemos um novo exemplo para o qual faremos a mesma análise do exemplo anterior. O exemplo que se segue é de um circuito com um único par de nós possuindo também fontes dependentes:

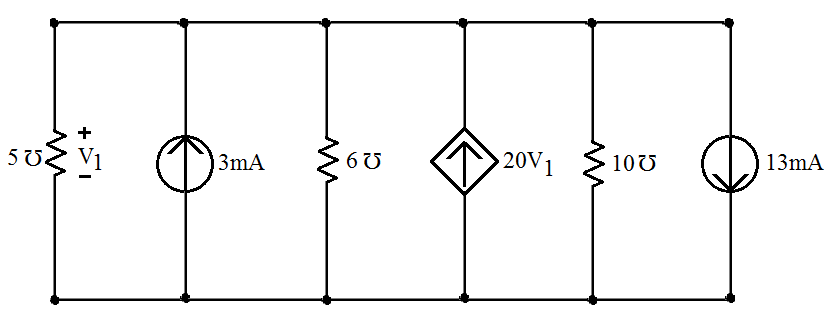
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes.

Como se pode verificar, a tensão $V_1$ aplicada sobre a condutância de 5 está também aplicada sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a seta dirigida para o nó inferior e aplicamos a lei dos nós.

$5V_1-0,003+6V_1-20V_1+10V_1+0,013=0$

$1V_1=-0,003-0,013\to V_1=-0,01V$

Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida ou consumida por cada um dos elementos.

Na condutância 5

$i_5=5V_1=-0,05A$

$P_5=5V_1^2=5(-0,01{)}^2=5.10^{-4}W$

Na condutância 6

$i_6=6V_1=-0,06A$

$P_6=6V_1^2=5(-0,01{)}^2=6.10^{-4}W$

Na condutância 10

$i_{10}=10V_1=-0,1A$

$P_{10}=10V_1^2=10(-0,01{)}^2=1.10^{-3}W$

Potência fornecida pela fonte de 3mA

$P_{f3ma}=0,003V_1=-0,3.10^{-4}W;P_a=0,3.10^{-4}W$

Potência fornecida pela fonte de 13mA

$P_{f13ma}=-0,013V_1=-1,3.10^{-4}W$

Potência fornecida pela fonte dependente

$P_{f20Vx}=20V_1.V_1=20V_1^2=20(-0,01{)}^2=20.10^{-4}W$

Por último, fazemos o balanço das potências

$\sum _{}^{}{P}_f=1,3.10^{-4}+20.10^{-4}=21,3.10^{-4}W$

$\sum _{}^{}{P}_a=5.10^{-4}+6.10^{-4}+0,3.10^{-4}=21,3.10^{-4}W$

2 Exercício de fixação

[1] Fonte independente de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito.

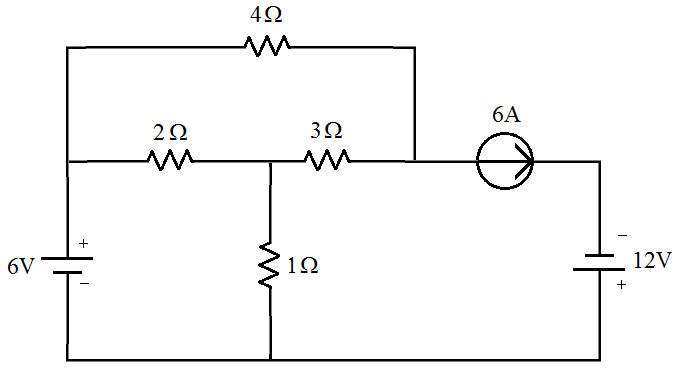
Solução

malha 1 $-6+2(i_1-i_2)+1(i_1-i_3)=0\to -6+2i_1-2i_2+1_1-6=0\to 3i_1-2i_2=12$ malha 2 $4i_2+3(i_2-i_3)+2(i_2-i_1)=0\to 4i_2+3i_2-18+2i_2-2i_1=0\to -2i_1+9_{i}2=18$ Resolvendo o sistema (Cramer) $\mathrm{\Delta }=\left|\begin{array}{cc}3& -2\\ -2& 9\end{array}\right|.\left|\begin{array}{c}12\\ 18\end{array}\right|$ $\mathrm{\Delta }=\left|\begin{array}{cc}3& -2\\ -2& 9\end{array}\right|=27-(4)\mathrm{\Delta }=23$ $\mathrm{\Delta }{i}_1=\left|\begin{array}{cc}12& -2\\ 18& 9\end{array}\right|=108-(-36)\mathrm{\Delta }{i}_1=144$ $\mathrm{\Delta }{i}_2=\left|\begin{array}{cc}3& 12\\ -2& 18\end{array}\right|=54-(-24)\mathrm{\Delta }{i}_2=78$ $i_1=\frac{\mathrm{\Delta }{i}_1}{\mathrm{\Delta }}=\frac{144}{23}{i}_1=6,26A$ $i_2=\frac{\mathrm{\Delta }{i}_2}{\mathrm{\Delta }}=\frac{78}{23}{i}_2=3,39A$

[2] Fonte dependente de corrente na malha. Determinas as correntes do circuito abaixo, a tensão e as potências dissipadas em todos os elementos do circuito.

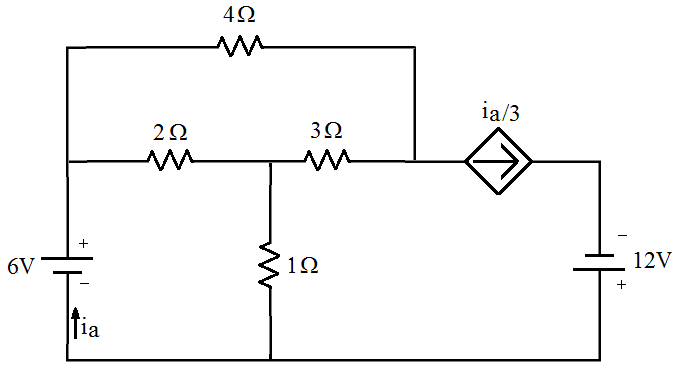
Solução

malha 1 $-6+2(i_1-i_2)+1(i_1-i_3)=0\to -6+2i_1-2i_2+i_1-i_3=0\to 3i_1-2i_2-i_3=6$ malha 2 $4i_2+3(i_2-i_3)+2(i_2-i_1)=0\to 4i_2+3i_2-3i_3+2i_2-2i_1=0\to -2i_1+9i_2-3i_3=0$ malha 3 $i_3=\frac{i_a}{3}$ Se $i_1=i_{a}logo{i}_3=\frac{i_1}{3}$ Resolvendo o sistema $3i_1-2i_2-i_3=6\to 3i_1-2i_2-\frac{i_1}{3}=6\to \frac{8i_1}{3}-2i_2=6$ $-2i_1+9i_2-3i_3=0\to -2i_1+9i_2-3\frac{i_1}{3}=0\to -3i_1+9i_2=0$ $\mathrm{\Delta }=\left|\begin{array}{cc}\frac{8}{3}& -2\\ -3& 9\end{array}\right|.\left|\begin{array}{c}6\\ 0\end{array}\right|$ $\mathrm{\Delta }=\left|\begin{array}{cc}\frac{8}{3}& -2\\ -3& 9\end{array}\right|=24-(6)\mathrm{\Delta }=18$ $\mathrm{\Delta }{i}_1=\left|\begin{array}{cc}6& -2\\ 0& 9\end{array}\right|=54-(0)\mathrm{\Delta }{i}_1=54$ $\mathrm{\Delta }{i}_2=\left|\begin{array}{cc}\frac{8}{3}& 6\\ -3& 0\end{array}\right|=0-(-18)\mathrm{\Delta }{i}_2=18$ $i_1=\frac{\mathrm{\Delta }{i}_1}{\mathrm{\Delta }}=\frac{54}{18}{i}_1=3A$ $i_2=\frac{\mathrm{\Delta }{i}_2}{\mathrm{\Delta }}=\frac{18}{18}{i}_2=1A$ $i_3=\frac{i_1}{3}=\frac{3}{3}{i}_3=1A$

3 Exercício

Encontra as correntes do circuito abaixo e calcule a potência de todos os elementos.

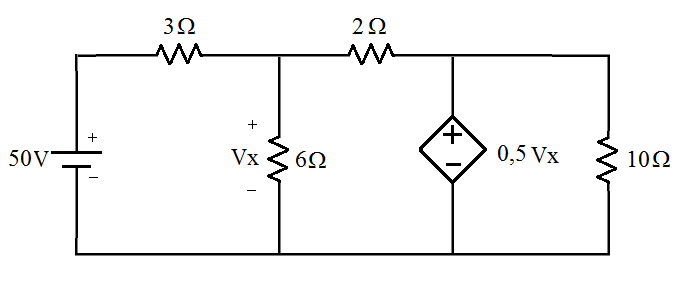
4 Referências

[1] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo3_ckt1.pdf

---

<<	<>	>>