CAL2-EngTel (Plano de Ensino)
Ir para navegação
Ir para pesquisar

|
MINISTÉRIO DA EDUCAÇÃO |
Plano de Ensino de 2012-2 - atual
- Dados gerais
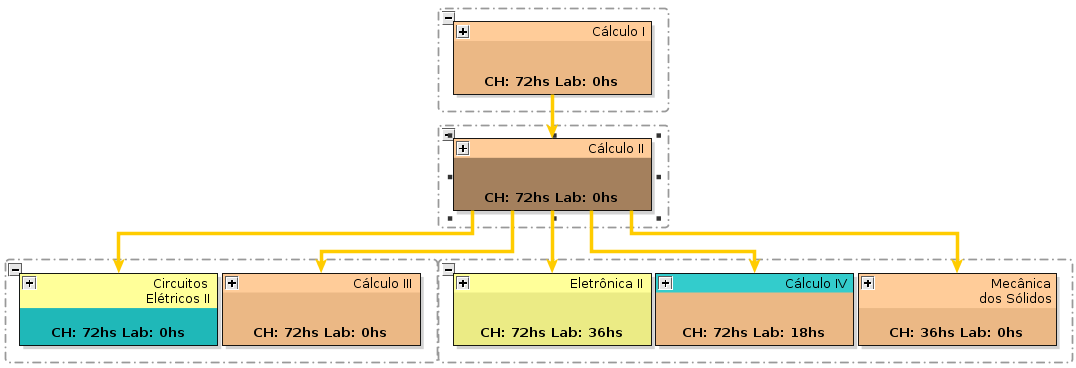
- COMPONENTE CURRICULAR: CAL2 - CÁLCULO II
- CARGA HORÁRIA: 4 HORAS/SEMANA 72 HORAS. TEÓRICA = 72 HORAS. LABORATÓRIO = 0 HORAS
- CÓDIGO: CAL29002
- PRÉ REQUISITOS: CAL1
- DISCIPLINAS SUCESSORAS: CAL3, CAL4, ELA1, SIS1, MEC, CIE1
- MÓDULO BÁSICO
- Objetivos
- Ao concluir o componente curricular o discente deverá ser capaz de:
- 1. Usar conhecimentos relacionados com equações diferenciais, transformadas de Laplace e funções de várias variáveis.
- 2. Identificar formas e tipos de equações diferenciais.
- 3. Resolver equações diferenciais de primeira e segunda ordem.
- 4. Aplicar transformada de Laplace.
- 5. Compreender o conceito de derivada e integral para funções de várias variáveis.
- 6. Calcular derivadas e integrais de funções de várias variáveis.
- Ementa
- Equações diferenciais ordinárias: Equações separáveis. Equações diferenciais exatas. Equações homogêneas. Equações diferenciais lineares de primeira e segunda ordem. Aplicações de equações diferenciais. Transformada de Laplace. Solução de equações diferenciais com Laplace. Funções de várias variáveis. Limite e continuidade das funções de várias variáveis. Derivadas parciais. Diferenciais e aplicações das derivadas parciais. Coordenadas polares, esféricas e cilíndricas.
- Conteúdo Programático
- 1.Introdução as equações diferenciais. Equações diferenciais de primeira ordem: teoria preliminar, variáveis separáveis (4h).
2.Equações homogêneas, equações exatas e lineares, equações de Bernoulli e Clairaut (12h).
3.Método de Picard. Aplicações de equações diferenciais de primeira ordem: trajetórias ortogonais, aplicações de equações lineares e não-lineares (8h).
4.Equações diferenciais lineares de ordem superior. Construindo uma segunda solução a partir de uma solução conhecida, equações lineares homogêneas com coeficientes constantes, coeficientes indeterminados, variação dos parâmetros (8h).
5.Aplicações de equações diferenciais de segunda ordem: modelos vibratórios. Equações diferenciais com coeficientes variáveis (6h).
6.Transformada de Laplace. Solução de equações diferenciais usando Laplace (12h).
7 Funções de várias variáveis. Limite e continuidade das funções de várias variáveis (4h).
8.Derivadas parciais. Diferenciais e aplicações das derivadas parciais (4h).
9. Coordenadas polares, esféricas e cilíndricas (8h).
Avaliações (6h).
- Estratégias de ensino utilizadas
- Aulas expositivas e dialogadas com o uso de lousa, giz, projetor multimídia, resolução de exercícios e utilização de softwares matemáticos.
- Critérios e instrumentos de avaliação
- A avaliação compreende os seguintes elementos:
- 1. Desempenho em sala de aula;
- 2. Participação nas atividades curriculares;
- 3. Provas escritas;
- Observação
- As avaliações e recuperações serão realizadas no formato de prova escrita. Serão realizadas 3 avaliações regulares ao longo do semestre. Caso o aluno não obtenha nota superior a 6 (seis) em alguma das avaliações, realizará uma avaliação de recuperação obrigatória, no final do semestre, para cada uma dessas avaliações que não obteve nota superior a 6 (seis), com o conteúdo correspondente à mesma. A nota da recuperação substituirá a nota da prova regular que se está recuperando, caso seja maior que a mesma. Em caso contrário, a nota da prova regular permanecerá. A nota final do aluno na disciplina será a maior nota obtida nas 3 avaliações depois de devidamente substituídas pelas notas das recuperações. O aluno será considerado aprovado caso obtenha nota superior a 6 (seis) em todas as avaliações regulares ou depois de devidamente substituídas pelas notas das recuperações. Caso contrário será considerado reprovado.
- IMPORTANTE
- 1) Só realizarão as provas de recuperações os alunos que realizaram as provas regulares e obtiveram nota inferior a 6 (seis).
- 2) A pontuação das questões de cada prova poderá ser: (0); (0,25); (0,5); (0,75) ou 1,0. A soma das pontuações de cada questão será a nota final de cada avaliação. Caso a nota não seja inteira será utilizado o seguinte critério:
- n = nota
- x = número inteiro variando de 0 até 10.
- Caso n seja um número inteiro, a nota na avaliação será n.
- Caso n não seja um número inteiro, x<n<x+1, então:
- 1) n=x, se a parte decimal de n for inferior a 0,5.
- 2) n=x+1, se a parte decimal de n for igual ou superior a 0,5.
1 Bibliografia do PPCv2015-2
- Bibliografia Básica
- FLEMMING, DIVA. GONÇALVES, MIRIAN CÁLCULO B; 2ª ed. SÃO PAULO:Pearson, 2007. 448p. ISBN 9788576051169. Qtdade Na Biblioteca para a Disciplina:8
- STEWART, JAMES CÁLCULO Vol.2; trad.7ª ed. SÃO PAULO:Cengage Learning, 2014. 664p. ISBN 9788522112593. Qtdade Na Biblioteca para a Disciplina:4
- BOYCE, William Equações diferenciais elementares e problemas de valores de contorno; 9ª ed. Rio de Janeiro:LTC, 2010. 607p. ISBN 9788521617563. Qtdade Na Biblioteca para a Disciplina:2
- Bibliografia Complementar
- GUIDORIZZI, HAMILTON CÁLCULO Vol.2; 5ª ed. [S.l]:LTC, 2001. 496p. ISBN 9788521612803. Qtdade Na Biblioteca para a Disciplina:4
- Kaplan, Wilfred; Lewis, Donald J. Calculus and Linear Algebra. Vol. 2: Vector Spaces, Many-Variable Calculus, and Differential Equations; ed. [S.l]:University of Michigan Library, . 606p. ISBN . "Disponível em: http://quod.lib.umich.edu/cgi/p/pod/dod-idx/.pdf?c=spobooks;idno=5597602.0002.001"Qtdade Na Biblioteca para a Disciplina:x
- MOTTA, Alexandre Equações diferenciais : introdução; 1ª ed. Florianópolis:IFSC, 2009. 136p. ISBN 9788562798023. Qtdade Na Biblioteca para a Disciplina:2
- Spiegel, Murray R. Manual de fórmulas e tabelas matemáticas; ed. Porto Alegre:Bookman, 2004. 352p. ISBN 8536303492. Qtdade Na Biblioteca para a Disciplina:2
- LEITHOLD, LOUIS O CÁLCULO COM GEOMETRIA ANALÍTICA Vol.2; 3ª ed. São Paulo:HABRA, 1994. 426p. ISBN 9788529402062. Qtdade Na Biblioteca para a Disciplina:2
2 Bibliografia Inicialmente Sugerida
- Bibliografia Básica
- FLEMMING, DIVA. GONÇALVES, MIRIAN CÁLCULO B; 2ª ed. SÃO PAULO:Pearson, 2007. 448p. ISBN 9788576051169
- BOYCE, William Equações diferenciais elementares e problemas de valores de contorno; 9ª ed. Rio de Janeiro:LTC, 2010. 607p. ISBN 9788521617563
- STEWART, JAMES CÁLCULO Vol.2; trad.7ª ed. SÃO PAULO:Cengage Learning, 2014. 664p. ISBN 9788522112593
- Bibliografia Complementar
- LEITHOLD, LOUIS O CÁLCULO COM GEOMETRIA ANALÍTICA Vol.2; 3ª ed. São Paulo:HABRA, 1994. 426p. ISBN 9788529400945
- GUIDORIZZI, HAMILTON CÁLCULO Vol.4; 5ª ed. [S.l]:LTC, 2001. 548p. ISBN 9788521613305
- GUIDORIZZI, HAMILTON CÁLCULO Vol.2; 5ª ed. [S.l]:LTC, 2001. 496p. ISBN 9788521612803
- MOTTA, Alexandre Equações diferenciais : introdução; 1ª ed. Florianópolis:IFSC, 2009. 136p. ISBN 9788562798023
3 ANEXOS