Mudanças entre as edições de "VSWR, Linha sem perdas"
| (5 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
| + | == Onda estacionária e VSWR == | ||
| + | |||
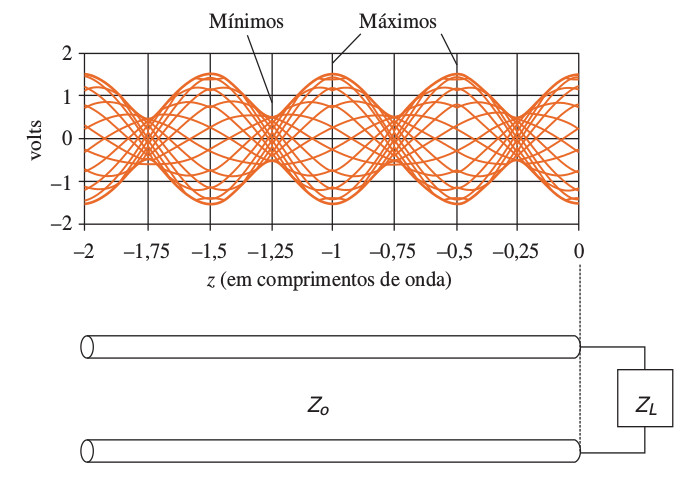
Na linha de transmissão a propagação das ondas incidente e refletida cria um padrão de onda estacionária (figura 1). | Na linha de transmissão a propagação das ondas incidente e refletida cria um padrão de onda estacionária (figura 1). | ||
| Linha 8: | Linha 10: | ||
| − | O parâmetro utilizado para medir ou indicar a "quantidade" de onda | + | O parâmetro utilizado para medir ou indicar a "quantidade" de onda estacionária ou de reflexão de onda numa linha de transmissão é a relação de onda estacionária (VSWR ou ROTE). Esse é definido como a razão entre as amplitudes máxima e a mínima da onda estacionária entre um pico e um vale consecutivo: |
| Linha 20: | Linha 22: | ||
| − | substituindo <math>V_o^-</math> por <math>\ | + | substituindo <math>V_o^-</math> por <math>\Gamma_L V_o^+</math> temos: |
| − | ::::<math>VSWR = {|V_o^+ + \ | + | ::::<math>VSWR = {|V_o^+ + \Gamma_L V_o^+| \over |V_o^+ - \Gamma_L V_o^+|}</math> |
{| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| − | | <math>VSWR = {1 + |\ | + | | <math>VSWR = {1 + |\Gamma_L| \over 1 - |\Gamma_L|}</math> |
|} | |} | ||
| + | |||
| + | |||
| + | A VSWR passa informação sobre a quantidade de potência enviada para a carga. Como o valor da VSWR é diretamente relacionado com <math> \Gamma_L</math> seu valor irá variar de: | ||
| + | |||
| + | |||
| + | :::: VSWR= 1, quando <math>|\Gamma_L| = 0</math> e não há potência de retorno, toda a potência que chega no final da linha é enviada para carga. | ||
| + | |||
| + | :::: <math>VSWR = \infty</math>, quando <math>|\Gamma_L| = 1</math> e todo a potência retorna, nenhuma potência é entregue a carga. | ||
| + | |||
| + | == Perda de Retorno (RL) == | ||
| + | |||
| + | Um segundo parâmetro fornece informações sobre a potência entregue para a carga, é a Perda de Retorno, que é definida por: | ||
| + | |||
| + | |||
| + | :::: <math>RL= 10 log ({P_{refletida} \over P_{incidente}})</math> | ||
| + | |||
| + | |||
| + | Um valor de RL = 10 dB indica que 10% da potência foi refletida e 90% foi para a carga. | ||
== Linha sem perdas == | == Linha sem perdas == | ||
| Linha 85: | Linha 105: | ||
=== Impedância de entrada, <math>Z_in</math> na linha sem perdas === | === Impedância de entrada, <math>Z_in</math> na linha sem perdas === | ||
| − | Em relação a <math> | + | Em relação a <math>Z_{in}</math> temos: |
| − | ::::<math>Z_{in( | + | ::::<math>Z_{in(-l)}= Z_o { Z_L (e^{\gamma l} + e^{-\gamma l}) + Z_o(e^{\gamma l} - e^{-\gamma l}) \over Z_L (e^{\gamma l} - e^{-\gamma l}) + Z_o (e^{\gamma l} + e^{-\gamma l})}</math> |
| − | ::::<math>Z_{in | + | ::::<math>Z_{in}= Z_o { Z_L ((e^{\alpha l} e^{j\beta l})+ (e^{-\alpha l} e^{-j\beta l})) + Z_o((e^{\alpha l} e^{j\beta l})- (e^{-\alpha l} e^{-j\beta l})) \over Z_L ((e^{\alpha l} e^{j\beta l}) - (e^{-\alpha l} e^{-j\beta l})) + Z_o ((e^{\alpha l} e^{j\beta l}) + (e^{-\alpha l} e^{-j\beta l}))}</math> |
| + | |||
como α = 0: | como α = 0: | ||
| − | ::::<math>Z_{in | + | ::::<math>Z_{in}= Z_o { Z_L ( e^{j\beta l}+ e^{-j\beta l}) + Z_o( e^{j\beta l}- e^{-j\beta l}) \over Z_L ( e^{j\beta l} - e^{-j\beta l}) + Z_o ( e^{j\beta l} + e^{-j\beta l})}</math> |
e da identidade de Euler: | e da identidade de Euler: | ||
| − | ::::<math>e^{-j\beta | + | |
| + | ::::<math>e^{-j\beta l} = cos \beta l - j sen \beta l</math> | ||
| − | ::::<math>e^{j\beta z} = cos \beta | + | ::::<math>e^{j\beta z} = cos \beta l + j sen \beta l</math> |
| − | ::::<math>Z_{in(z)}= Z_o { Z_L ( cos \beta | + | ::::<math>Z_{in(z)}= Z_o { Z_L ( cos \beta l{\color{red}+ j sen \beta l} + cos \beta l {\color{red} - j sen \beta l)} + Z_o( {\color{red} cos \beta l} + j sen \beta l {\color{red}- cos \beta l} + j sen \beta l) \over Z_L ( {\color{red}cos \beta l} + j sen \beta l {\color{red} - cos \beta l} + j sen \beta l) + Z_o ( cos \beta l {\color{red} + j sen \beta l} + cos \beta l - {\color{red}j sen \beta l)}}</math> |
| − | ::::<math>Z_{in | + | ::::<math>Z_{in}= Z_o { Z_L ( cos \beta l) + Z_o (jsen \beta l) \over Z_L (jsen \beta l)+ Z_o (cos \beta l)}</math> |
| − | |||
| + | dividindo numerador e denominador por <math>cos \beta l</math>: | ||
| − | |||
{| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| − | |<math>Z_{in | + | |<math>Z_{in}= Z_o { Z_L + jZ_o (tan \beta l) \over Z_o + jZ_L (tan \beta l)}</math> |
|} | |} | ||
Edição atual tal como às 09h51min de 23 de outubro de 2015
Onda estacionária e VSWR
Na linha de transmissão a propagação das ondas incidente e refletida cria um padrão de onda estacionária (figura 1).
figura 1: onda estacionária para uma linha sem perdas e com
fonte: WENTWORTH, Stuart M. Eletromagnetismo Aplicado: Abordagem Antecipada das Linhas de Transmissão. Bookman, 2009.
O parâmetro utilizado para medir ou indicar a "quantidade" de onda estacionária ou de reflexão de onda numa linha de transmissão é a relação de onda estacionária (VSWR ou ROTE). Esse é definido como a razão entre as amplitudes máxima e a mínima da onda estacionária entre um pico e um vale consecutivo:
- (1)
substituindo por temos:
A VSWR passa informação sobre a quantidade de potência enviada para a carga. Como o valor da VSWR é diretamente relacionado com seu valor irá variar de:
- VSWR= 1, quando e não há potência de retorno, toda a potência que chega no final da linha é enviada para carga.
- , quando e todo a potência retorna, nenhuma potência é entregue a carga.
Perda de Retorno (RL)
Um segundo parâmetro fornece informações sobre a potência entregue para a carga, é a Perda de Retorno, que é definida por:
Um valor de RL = 10 dB indica que 10% da potência foi refletida e 90% foi para a carga.
Linha sem perdas
Muitas linhas de transmissão são formadas por bons condutores e isolantes. Essas linhas apresentam valores de R e G muito pequenos e como:
Ao fazermos essas aproximações estamos considerando que a linha não tem perdas, como podemos observar no coeficiente de propagação (γ)
- (2)
como e a equação (2) não apresenta parte real .
Impedância característica de uma linha sem perdas
| a impedância característica da uma linha sem perdas é resistiva !!! |
Potência incidente de uma linha sem perdas
Uma vez que é resistiva e , a potência incidente de uma linha sem perdas passa a ser:
Impedância de entrada, na linha sem perdas
Em relação a temos:
como α = 0:
e da identidade de Euler:
dividindo numerador e denominador por :