Equações Telegráficas - Equações da Onda Viajante

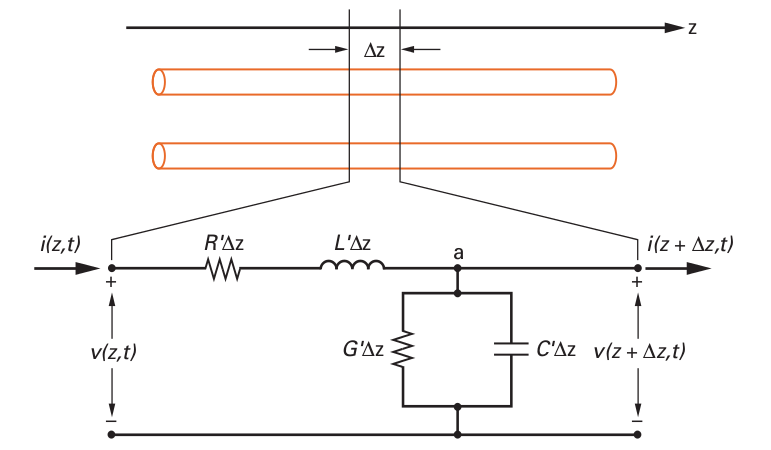
A figura abaixo mostra uma seção infinitesimal de uma linha de transmissão sendo submetida a uma tensão e percorrida por uma corrente. A partir da análise das tensões e correntes instantâneas desse modelo chegaremos nas equações da onda viajante na linha de transmissão.

fonte: WENTWORTH, Stuart M. Eletromagnetismo Aplicado: Abordagem Antecipada das Linhas de Transmissão. Bookman, 2009.

A partir de Kirchhoff para a malha temos:

$v(z,t)-v(z+\Delta z,t)=i(z,t)R'\Delta z+L'\Delta z{\partial i(z,t) \over \partial t}$ (1)

E de Kirchhoff para o nó a:

$i(z,t)-i(z+\Delta z,t)=v(z+\Delta z,t)G'\Delta z+C'\Delta z{\partial v(z+\Delta z,t) \over \partial t}$ (2)

Dividindo as equações (1) E (2) por $\Delta z$ e fazendo $\Delta z{\longrightarrow 0}$:

$\lim _{\Delta _{z}\to 0}{v(z,t)-v(z+\Delta z,t) \over \Delta z}=i(z,t)R'+L'{\partial i(z,t) \over \partial t}$ (3)

$\lim _{\Delta _{z}\to 0}{i(z,t)-i(z+\Delta z,t) \over \Delta z}=v(z+\Delta z,t)G'+C'{\partial v(z,t) \over \partial t}$ (4)

Os limites nas equações (4) e (5) correspondem a definição de derivada, portanto podemos escrever as equações telegráficas:

$-{\partial v(z,t) \over \partial z}=i(z,t)R'+L'{\partial i(z,t) \over \partial t}$ (5)

$-{\partial i(z,t) \over \partial z}=v(z,t)G'+C'{\partial v(z,t) \over \partial t}$ (6)

Solução das equações telegráficas via uma função harmônica no tempo (sinusoidal)

Vamos obter a solução para as equações telegráficas a partir de uma solução harmônica no tempo, isto é, vamos considerar que a tensão v(z,t) é cossenoidal.

A equação de uma onda de tensão cossenoidal e descrita por:

$v(z,t)=v(z)cos(wt+\phi (z))$ (7)

v(z) e $\phi (z)$ são funções apenas da posição z

Considerando a identidade de Euler [ $e^{j\psi }=cos\psi +jsen\psi$], podemos reescrever a equação (7) como:

$\Re \left\{e^{j\psi }\right\}=cos\psi$ (8)

$v(z,t)=v(z)cos(wt+\phi \phi (z))=\Re \left\{v(z)e^{j(wt+\phi (z))}\right\}$ $=\Re \left\{v(z)e^{+j\phi (z)}e^{jwt}\right\}$ (9)

Da representação de função complexa:

$V(z)=v(z)e^{-j\phi (z)}$ (10)

Portanto:

$v(z)=|V(z)|$ (11)

$\phi (z)=arg\left\{V(z)\right\}$ (12)