Mudanças entre as edições de "Equações Telegráficas - Equações da Onda Viajante"
(Criou página com 'A figura abaixo mostra uma seção infinitesimal de uma linha de transmissão sendo submetida a uma tensão e percorrida por uma corrente. A partir da análise das tensões e co...') |
|||
| (43 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
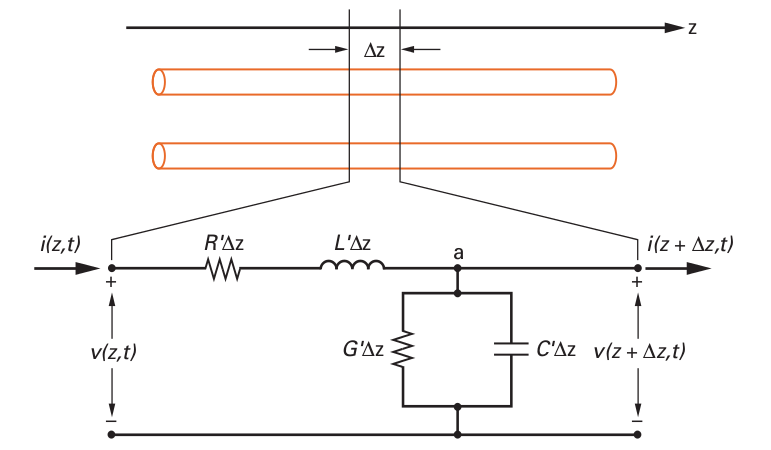
| − | A figura | + | A figura 1 mostra uma seção infinitesimal de uma linha de transmissão sendo submetida a uma tensão e percorrida por uma corrente. A partir da análise das tensões e correntes instantâneas dessa seção chegaremos nas equações da onda viajante na linha de transmissão. |
[[Arquivo:Modelo_distribuido_com_corrente_e_tensao_instantaneas.png]] | [[Arquivo:Modelo_distribuido_com_corrente_e_tensao_instantaneas.png]] | ||
| + | Figura 1: Seção infinitesimal de uma linha de transmissão. | ||
fonte: WENTWORTH, Stuart M. Eletromagnetismo Aplicado: Abordagem Antecipada das Linhas de Transmissão. Bookman, 2009. | fonte: WENTWORTH, Stuart M. Eletromagnetismo Aplicado: Abordagem Antecipada das Linhas de Transmissão. Bookman, 2009. | ||
| + | |||
| + | '''A partir de Kirchhoff para a malha temos:''' | ||
| + | |||
| + | |||
| + | :::::<math>\ v(z,t) - v(z+\Delta z,t) = i(z,t) R'\Delta z + L'\Delta z{\partial i(z,t) \over \partial t} </math> (1) | ||
| + | |||
| + | |||
| + | '''E de Kirchhoff para o nó <span style="color: red"> a </span>:''' | ||
| + | |||
| + | |||
| + | :::::<math>\ i(z,t) - i(z+\Delta z,t) = v(z+\Delta z,t) G'\Delta z + C'\Delta z{\partial v(z+\Delta z,t) \over \partial t} </math> (2) | ||
| + | |||
| + | |||
| + | Dividindo as equações (1) E (2) por <math>\Delta z</math> e fazendo <math>\Delta z {\longrightarrow 0}</math>: | ||
| + | |||
| + | |||
| + | :::::<math>\ \lim_{\Delta_z \to 0} {v(z,t) - v(z+\Delta z,t) \over \Delta z} = i(z,t) R' + L'{\partial i(z,t) \over \partial t} </math> (3) | ||
| + | |||
| + | |||
| + | |||
| + | :::::<math>\lim_{\Delta_z \to 0} {i(z,t) - i(z+\Delta z,t) \over \Delta z} = v(z,t) G' + C'{\partial v(z,t) \over \partial t} </math> (4) | ||
| + | |||
| + | |||
| + | |||
| + | Os limites nas equações (4) e (5) correspondem a definição de derivada, portanto podemos escrever as equações telegráficas: | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | | <math>\ -{\partial v(z,t) \over \partial z} = i(z,t) R' + L'{\partial i(z,t) \over \partial t} </math> (5) | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | {|class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>\ -{\partial i(z,t) \over \partial z} = v(z,t) G' + C'{\partial v(z,t) \over \partial t} </math> (6) | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | == Solução das equações telegráficas via uma função harmônica no tempo (sinusoidal)== | ||
| + | |||
| + | Vamos obter a solução para as equações telegráficas a partir de uma solução harmônica no tempo, isto é, vamos considerar que a tensão v(z,t) é cossenoidal. | ||
| + | |||
| + | A equação de uma onda de tensão cossenoidal e descrita por: | ||
| + | |||
| + | |||
| + | :::::<math>\ v(z,t) = v(z) \cos(wt+\psi (z))</math> (7) | ||
| + | |||
| + | |||
| + | v(z) e ψ (z) são funções apenas da posição z. | ||
| + | |||
| + | Considerando a identidade de Euler [ <math>e^{j\psi} = cos \psi + jsen \psi</math>], podemos reescrever a equação (7) como: | ||
| + | |||
| + | |||
| + | :::::<math>\ \Re\left \{ e^{j\psi}\right \}= cos \psi</math> (8) | ||
| + | |||
| + | |||
| + | |||
| + | :::::<math>\ v(z,t) = v(z) cos(wt+ \psi (z)) = \Re \left \{v(z) e^{j(wt+\psi(z))}\right \}</math> | ||
| + | |||
| + | |||
| + | |||
| + | :::::<math>=\Re\left \{v(z)e^{+j \psi(z)} e^{jwt}\right \}</math> (9) | ||
| + | |||
| + | |||
| + | Da representação de função complexa: | ||
| + | |||
| + | |||
| + | :::::<math>\ V(z)= v(z) e^{-j\psi(z)}</math> (10) | ||
| + | |||
| + | |||
| + | Portanto: | ||
| + | |||
| + | |||
| + | :::::<math>\ v(z)=|V(z)|</math> (11) | ||
| + | |||
| + | |||
| + | :::::<math>\ \psi(z)= arg \left \{V(z)\right \}</math> (12) | ||
| + | |||
| + | |||
| + | |||
| + | A análise feita considerando uma onda de tensão tem sua equivalente em termos de uma onda de corrente. | ||
| + | |||
| + | |||
| + | |||
| + | === Equação da onda viajante === | ||
| + | |||
| + | |||
| + | Lembrando que: | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ {\partial \Re \left \{ e^{jwt} \right \} \over \partial t} ={\partial \Re \left \{ cos (wt) + jsen (wt) \right \} \over \partial t}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ = {\partial cos(wt) \over \partial t} = -wsen (wt)</math> | ||
| + | |||
| + | |||
| + | e | ||
| + | |||
| + | |||
| + | ::::<math>\Re \left \{ jwe^{jwt} \right \}= \Re \left \{jw( cos(wt) + jsen (wt)) \right \}</math> | ||
| + | |||
| + | |||
| + | ::::<math> = -wsen (wt)</math> | ||
| + | |||
| + | |||
| + | temos: | ||
| + | |||
| + | |||
| + | ::::<math>{\partial \Re \left \{ e^{jwt} \right \} \over \partial t} =\Re \left \{ jwe^{jwt} \right \}</math> | ||
| + | |||
| + | |||
| + | portanto: | ||
| + | |||
| + | |||
| + | ::::<math>{\partial v(z,t) \over \partial t}= {\partial \Re \left \{ V(z)e^{jwt} \right \} \over \partial t}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>{\partial v(z,t) \over \partial t}= V(z) {\partial \Re \left \{ e^{jwt} \right \} \over \partial t} = V(z) \Re \left \{ jwe^{jwt} \right \} </math> | ||
| + | |||
| + | |||
| + | ::::<math>{\partial v(z,t) \over \partial t}= jwV(z) </math> | ||
| + | |||
| + | |||
| + | Utilizando a notação de função complexa e substituindo v(z,t) e i(z,t) nas equações telegráficas (5) e (6): | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | | <math> {\partial V(z) \over \partial z} = -(R + jwL) I(z) </math> (14) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | | <math>{\partial I(z) \over \partial z} = -(G + jwC) V(z) </math> (15) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Derivando a primeira equação telegráfica (14) em função de z: | ||
| + | |||
| + | |||
| + | ::::<math> {\partial^2 V(z) \over \partial z^2} = -(R + jwL) {\partial I(z) \over \partial z} </math> | ||
| + | |||
| + | |||
| + | e substituindo <math>{\partial I(z) \over \partial z}</math> pela segunda equação telegráfica (15) temos: | ||
| + | |||
| + | |||
| + | ::::<math> {\partial^2 V(z) \over \partial z^2} = (R + jwL) (G + jwC) V(z) </math> (16) | ||
| + | |||
| + | |||
| + | fazendo <math> \gamma^2 = (R + jwL) (G + jwC)</math> isto é <math> \gamma = \sqrt {(R + jwL) (G + jwC)} = \alpha + j\beta </math> | ||
| + | |||
| + | |||
| + | ::::<math> {\partial^2 V(z) \over \partial z^2} -\gamma^2 V(z) =0 </math> (17) | ||
| + | |||
| + | |||
| + | A equação (17) é uma equação diferencial linear homogênea de segunda ordem. Uma solução para esta equação é uma função exponencial, como: | ||
| + | |||
| + | |||
| + | ::::<math>V(z) = Ae^{\lambda z}</math> (18) | ||
| + | |||
| + | |||
| + | onde A e <math>\lambda</math> são constantes arbitrárias. | ||
| + | |||
| + | |||
| + | Derivando duas vezes a função (18) em função de z temos: | ||
| + | |||
| + | |||
| + | ::::<math>{\partial^2 V(z) \over \partial^2 z} =\lambda^2 Ae^{\lambda z}</math> | ||
| + | |||
| + | |||
| + | e a equação (17) pode ser reescrita como: | ||
| + | |||
| + | |||
| + | ::::<math>\lambda^2Ae^{\lambda z} - \gamma^2 Ae^{\lambda z} = 0</math> | ||
| + | |||
| + | |||
| + | ou | ||
| + | |||
| + | |||
| + | ::::<math>\lambda^2 - \gamma^2 = 0 </math> ou <math>(\lambda+\gamma)(\lambda-\gamma) = 0 </math> | ||
| + | |||
| + | |||
| + | Uma solução para essa equação é <math>\lambda = -\gamma </math>, portanto: | ||
| + | |||
| + | |||
| + | ::::<math>V(z) = Ae^{-\gamma z}</math> | ||
| + | |||
| + | |||
| + | Retornando para a representação no tempo: | ||
| + | |||
| + | |||
| + | ::::<math>v(z,t) = Ae^{-\alpha z} cos (wt - \beta z)</math> | ||
| + | |||
| + | |||
| + | Substituindo A por uma constante mais significativa <math>V_o^+</math> | ||
| + | |||
| + | |||
| + | ::::<math>v(z,t) = V_o^+e^{-\alpha z} cos (wt - \beta z)</math> (19) | ||
| + | |||
| + | |||
| + | A equação (19) corresponde a uma onda de tensão se propagando na direção +z com amplitude em z=0 de <math>V_o^+</math> | ||
| + | |||
| + | |||
| + | |||
| + | Da segunda solução <math>\lambda = \gamma </math> temos: | ||
| + | |||
| + | |||
| + | ::::<math>v(z,t) = V_o^-e^{\alpha z} cos (wt + \beta z)</math> (20) | ||
| + | |||
| + | |||
| + | A equação (20) corresponde a uma onda de tensão se propagando na direção -z com amplitude em z=0 de <math>V_o^-</math> | ||
| + | |||
| + | |||
| + | A resposta completa da equação (18) é a equação da onda viajante no tempo, a qual é obtida pela soma das soluções individuais da equação diferencial: | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | | <math>v(z,t) = V_o^+e^{-\alpha z} cos (wt - \beta z) + V_o^-e^{\alpha z} cos (wt + \beta z)</math> (21) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Uma análise equivalente poderia ser realizada para i(z,t) obtendo: | ||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>i(z,t) = I_o^+e^{-\alpha z} cos (wt - \beta z) + I_o^-e^{\alpha z} cos (wt + \beta z)</math> (22) | ||
| + | |} | ||
Edição atual tal como às 09h17min de 13 de outubro de 2015
A figura 1 mostra uma seção infinitesimal de uma linha de transmissão sendo submetida a uma tensão e percorrida por uma corrente. A partir da análise das tensões e correntes instantâneas dessa seção chegaremos nas equações da onda viajante na linha de transmissão.
Figura 1: Seção infinitesimal de uma linha de transmissão. fonte: WENTWORTH, Stuart M. Eletromagnetismo Aplicado: Abordagem Antecipada das Linhas de Transmissão. Bookman, 2009.
A partir de Kirchhoff para a malha temos:
- (1)
E de Kirchhoff para o nó a :
- (2)
Dividindo as equações (1) E (2) por e fazendo :
- (3)
- (4)
Os limites nas equações (4) e (5) correspondem a definição de derivada, portanto podemos escrever as equações telegráficas:
| (5) |
| (6) |
Solução das equações telegráficas via uma função harmônica no tempo (sinusoidal)
Vamos obter a solução para as equações telegráficas a partir de uma solução harmônica no tempo, isto é, vamos considerar que a tensão v(z,t) é cossenoidal.
A equação de uma onda de tensão cossenoidal e descrita por:
- (7)
v(z) e ψ (z) são funções apenas da posição z.
Considerando a identidade de Euler [ ], podemos reescrever a equação (7) como:
- (8)
- (9)
Da representação de função complexa:
- (10)
Portanto:
- (11)
- (12)
A análise feita considerando uma onda de tensão tem sua equivalente em termos de uma onda de corrente.
Equação da onda viajante
Lembrando que:
e
temos:
portanto:
Utilizando a notação de função complexa e substituindo v(z,t) e i(z,t) nas equações telegráficas (5) e (6):
| (14) |
| (15) |
Derivando a primeira equação telegráfica (14) em função de z:
e substituindo pela segunda equação telegráfica (15) temos:
- (16)
fazendo isto é
- (17)
A equação (17) é uma equação diferencial linear homogênea de segunda ordem. Uma solução para esta equação é uma função exponencial, como:
- (18)
onde A e são constantes arbitrárias.
Derivando duas vezes a função (18) em função de z temos:
e a equação (17) pode ser reescrita como:
ou
- ou
Uma solução para essa equação é , portanto:
Retornando para a representação no tempo:
Substituindo A por uma constante mais significativa
- (19)
A equação (19) corresponde a uma onda de tensão se propagando na direção +z com amplitude em z=0 de
Da segunda solução temos:
- (20)
A equação (20) corresponde a uma onda de tensão se propagando na direção -z com amplitude em z=0 de
A resposta completa da equação (18) é a equação da onda viajante no tempo, a qual é obtida pela soma das soluções individuais da equação diferencial:
| (21) |
Uma análise equivalente poderia ser realizada para i(z,t) obtendo:
| (22) |