ELD129002-Engtelecom (Diário) - Prof. Marcos Moecke

Registro on-line das aulas

Unidade 1 - Aula inicial, Introdução a disciplina

• 1 ENCONTRO

Unidade 1 - Aula inicial, Introdução a disciplina

Encontro 1 (15 fev) A página da UC contém os materiais que não alteram entre semestre. Relação com as outras UCs do Eixo Sistemas Computacionais (Marrom). Ver grafo do curriculo ELD129002 - ELETRÔNICA DIGITAL I (ELD1): Sistema de numeração e códigos. Lógica booleana. Circuitos combinacionais. Circuitos aritméticos. Linguagem de descrição de hardware. Implementação e teste de circuitos digitais. Projeto de circuitos lógicos. ELD129003 - ELETRÔNICA DIGITAL II (ELD2): Dispositivos lógicos programáveis. Circuitos sequenciais. Metodologia síncrona. Projeto hierárquico e parametrizado. Máquinas de estados finita. Register Transfer Methodology. Teste de circuitos digitais. Implementação em FPGA. Introdução a Linguagem de Descrição de Hardware. AOC129004 - ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES (AOC): Introdução à Arquitetura Computadores. Linguagem Assembly. Linguagem de Máquina. Programação Assembly. Modos de Endereçamento. Processo de compilação e carga de um programa. Introdução à Organização de Computadores. Organização Monociclo e Multiciclo. Pipeline. Memória e Sistema de E/S. MIC129007 - MICROCONTROLADORES (MIC): Introdução a Microcontroladores e Aplicações. Arquitetura de um microcontrolador. Pilha e Subrotinas. Interrupção. Contadores e Temporizadores. Interface com Periféricos. Programação em alto nível (ex.: C, C++ e RUST) para Microcontroladores: Mapeamento de tipos e estruturas de alto nível para sistemas com recursos limitados. Projeto de hardware e firmware com microcontroladores. STE129008 - STE - SISTEMAS EMBARCADOS (STE): Conceitos em Sistemas Embarcados. Metodologia de Desenvolvimento de Sistemas Embarcados. Sistemas Operacionais para Sistemas Embarcados. Ferramentas de desenvolvimento e depuração. Barramentos e dispositivos de acesso a redes. Desenvolvimento de Projeto. Nesta página está o Registro diário dos encontros e avaliações. A entrega de atividades e avaliações será através da plataforma Moodle. A inscrição dos alunos é automática a partir do SIGAA. Para a comunicação entre professor-aluno, além dos avisos no SIGAA, utilizaremos o chat institucional. A princípio todos os alunos já estão previamente cadastrados pelo seu email institucional. Confiram enviando uma mensagem de apresentação. Utilizaremos durante as aulas algumas ferramentas computacionas como o site do Falstad para entender circuitos digitais e fazer simulações básicas. Também utilizaremos os softwares Quartus Light e ModelSim instalados nas maquinas do laboratório para praticar a parte de programação de hardware (descrição de hardware). Esses softwares também podem ser usados através da Nuvem do IFSC.. LER PARA O PRÓXIMO ENCONTRO Capítulo 1. Do Zero ao Um, seções 1.1 a 1.3 do livro David Money Harris, B., & Harris Morgan Kaufman, S. L. (2013). Projeto Digital e Arquitetura de Computadores, diponibilizado gratuitamente pela www.imgtec.com.

Unidade 2 - Sistema de numeração e códigos

• 4 ENCONTROS

Unidade 2 - Sistema de numeração e códigos

Encontro 2 (20 fev) - Sistemas numéricos O ser humano precisa contar para determinar quantidades de coisas, com as quantidades ele pode fazer operações matemáticas e comparações. Os números permitem representar quantidades de forma simbólica. Os símbolos utilizados são chamados de dígitos. Em alguns sistemas a posição do símbolo faz diferença (sistemas posicionais), enquanto que em outros o símbolo já representa a quantidade. Dependendo do sistema podem existir diferentes tipos e quantidades de símbolos. Sistema decimal: É o sistema utilizado no dia a dia das tarefas diárias Utiliza 10 símbolos (dígitos). 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 É um sistema posicional, onde a posição do dígito tem um peso dado pela base (10) elevado ao expoente da posição. Exemplo: o número representado 135, corresponde a 1 centena (10² = 100), 3 dezenas (10¹ = 10) e 5 unidades (10⁰ = 1), pois 1*10² + 3*10¹ + 5*10⁰ = 1*100 + 3*10 + 5*1 = 100 + 30 + 5 = 135 Com o sistema podemos contar quantidades, representar quantidades inteiras e fracionárias, comparar valores (quantidades), fazer operações de soma, subtração, multiplicação, divisão, entre outras; Exemplos: Contar: …, 34, 35, 36, 37, … Somar: 21 + 46 + 100 = 100 + 20 + 40 + 1 + 6 = 100 + 60 + 7 = 167; Multiplicar: 3 x 6 = 6 + 6 + 6 = 18; Dividir: 35/7 = (5+ 5 + 5 + 5 + 5 + 5 +5)/7 = (5*7)/7 = 5; Representar frações: 12/10 = 1,2; 3/4 = 0,75 Comparar valores: 145 > 14,5; 230 = 2,3x102 Outros sistemas: Nos computadores e circuitos digitais, para fazer a representação de números são utilizadas normalmente duas tensões, sendo uma para representar o dígito “0” (0 volt), e outra para representar o dígito “1” ( X volts). Este sistema é chamado de sistema binário, pois utiliza apenas dois dígitos (0 e 1). O sistema também é posicional, e permite representar quantidades e fazer operações matemáticas e comparações OBS: Muitas vezes os números binários são representados através do sistema hexadecimal ou do sistema octal (já em desuso). Sistema binário: Utiliza apenas 2 símbolos (dígitos). 0 e 1 É um sistema posicional, onde a posição do dígito tem um peso dado pela base (2) elevado ao expoente da posição. Exemplo: o número representado 111, corresponde a 1 quadra (2² = 4), 1 dupla (2¹ = 2) e 1 unidade (2⁰ = 1). 1*2² + 1*2¹ + 1*2⁰ = 1*4 + 1*2 + 1*1 = 4 + 2 + 1 = 7 O que são bits, nibbles, bytes e word (palavra) de bits ↓msb lsb↓ 0 1 1 0 0 1 1 0 1 1 1 0 0 0 1 1 nibble nibble nibble nibble byte (MSB) byte (LSB) word (palavra) Note no quadro acima: o nibble corresponde ao grupo de 4 bits (meio byte) o byte corresponde ao grupo de 8 bits. Este grupo de 8 bits também é denominado de forma mais exata de octeto. a word corresponde ao grupo de 16 bits (as vezes 32 bits) a double word corresponte ao grupo de 32 bits (as vezes 64 bits) o bit menos significativo (lsb - less significative bit) o bit mais significativo (msb - most significative bit) o byte menos significativo (LSB - Less Significative Byte) o byte mais significativo (MSB - Most Significative Byte) Prefixos e multiplos utilizados para quantidades de informação Nome Símbolo Número de bytes Aproximação decimal Byte B / Byte 1 1 kilobyte kB / kByte $2^{10}$ $10^{3}$ (mil) Megabyte MB / MByte $2^{20}$ $10^{6}$ (milhão) Gigabyte GB / GByte $2^{30}$ $10^{9}$ (bilhão) Terabyte TB / TByte $2^{40}$ $10^{12}$ (trilhão) Petabyte PB / PByte $2^{50}$ $10^{15}$ (quadrilhão) PARA O PRÓXIMO ENCONTRO Ler capítulo 1. Do Zero ao Um, seção 1.4 do livro Projeto Digital e Arquitetura de Computadores, diponibilizado gratuitamente pela www.imgtec.com. Ver Slides - Sistemas Numéricos Ver mais sobre Byte ou Byte.en e os prefixos binários na Wikipedia Encontro 3 (22 fev) Conversão de bases entre sistemas numéricos Conversão entre os sistemas de numeração decimal - binário - hexadecimal. ver os slides - Sistemas Numéricos (conversão entre sistemas) Regra geral de conversão de valor para qualquer sistema de numeração Dividir o valor (número) pela base e obter o quociente e o resto. Dividir sucessivas vezes o quociente anterior até obter um quociente nulo. Os restos obtidos são os digitos que representam o valor (número) no novo sistema de numeração. O primeiro resto obtido é o dígito menos significativo. O último resto obtido é o dígito mais significativo. Regra geral de conversão de um sistema de numeração qualquer de base N para decimal Verifique a posição do ponto decimal. Os dígitos a esquerda do ponto decimal correspondem as posições 0, 1, 2, … . Se houver dígitos a direita do ponto decimal, eles correspondem as posições -1, -2, -3, … . A cada dígito é dado um peso correspondente ao valor da base elevada ao expoente Nposição. Multiplique os pesos pelos dígitos correspondentes. O valor final (em decimal) é a soma dos valores obtidos. posição k … 2 1 0 , -1 -2 … -l dígito dk d2 d1 d0 d-1 d-2 d-l peso Nk N2 N1 N0 N-1 N-2 N-l somar dk × Nk d2 × N2 d1 × N1 d0 × N0 d-1 × N-1 d-2 × N-2 d-l × N-l valor dk × Nk + d2 × N2 + d1 × N1 + d0 × N0 + d-1 × N-1 + d-2 × N-2 + d-l × N-l Códigos numéricos binários Número sem sinal (UNSIGNED) Neste caso apenas números inteiros naturais podem ser representados. Usando $N$ bits é possível representar números inteiros no intervalo de $[0,2^{N}-1]$. Por exemplo usando 8 bits => $[0,2^{8}-1]=[0,255]=[00000000_{2},11111111_{2}]$ bit 7 6 5 4 3 2 1 0 valor 1 0 1 0 0 1 1 1 peso 27 26 25 24 23 22 21 20 peso +128 +64 +32 +16 +8 +4 +2 +1 somar +128 +32 +4 +2 +1 resultado 128 + 32 + 4 + 2 + 1 = 167 Número com sinal (Sinal-Magnitude ou Magnitude e Sinal) Neste caso os números inteiros negativos são representados com 1 no msb, e o positivos com 0 no msb. Usando $N$ bits é possível representar números inteiros no intervalo de $[-(2^{N-1}-1),(2^{N-1}-1(]$. Nesta representação existem dois zeros, o +0 e o -0. Por exemplo usando 8 bits => $[-(2^{8-1}-1),(2^{8-1}-1)]=[-(2^{7}-1),(2^{7}-1)]=[-127,-0,+0,+127]=[11111111_{2},10000000_{2},00000000_{2},01111111_{2}]$ bit 7 6 5 4 3 2 1 0 peso 26 25 24 23 22 21 20 peso +64 +32 +16 +8 +4 +2 +1 valor 1 0 1 0 0 1 1 1 somar - +32 +4 +2 +1 resultado - ( 32 + 4 + 2 + 1) = - 39 valor 0 0 1 0 0 1 1 1 somar + +32 +4 +2 +1 resultado + ( 32 + 4 + 2 + 1) = +39 Número com sinal (Complemento de 2 ou SIGNED) Neste caso o msb corresponde ao peso negativo, de modo que ao colocar 1 no msb o número inteiro passa a ser negativo, e se o msb for 0, o número será positivo. Usando $N$ bits é possível representar números inteiros no intervalo de $[-2^{N-1},2^{N-1}-1]$. Nesta representação existem apenas um zero. Por exemplo usando 8 bits => $[-2^{N-1},2^{N-1}-1]=[-128,0,+127]=[10000000_{2},00000000_{2},01111111_{2}]$ Neste caso note que quando todos os bits são 1, o número representado será o -1, $11111111_{2}$ bit 7 6 5 4 3 2 1 0 peso 27 26 25 24 23 22 21 20 peso -128 +64 +32 +16 +8 +4 +2 +1 valor 1 0 1 0 0 1 1 1 somar -128 +32 +4 +2 +1 resultado - 128 + 32 + 4 + 2 + 1 = -128 + 39 = -89 valor 0 0 1 0 0 1 1 1 somar +32 +4 +2 +1 resultado 32 + 4 + 2 + 1 = +39 valor 1 1 1 1 1 1 1 1 somar -128 +64 +32 +16 +8 +4 +2 +1 resultado -128 + 64 + 32 +16 + 8 + 4 + 2 + 1 = -128 + 127 = -1 Comparação das representações O quadro abaixo mostra as representações em binário dos valores de +15 a -8 no sistema sem sinal (UNSIGNED), com signal-magnitude , com sinal em complemento de um , com sinal em complemento de dois (SIGNED). No quadro é importante notar que sempre os números negativos tem o msb = 1. Adicionalmente alguns sistemas possuem dois zeros (+0 e -0). No tipo SIGNED note que o valor máximo positivo será menor que o valor absoluto do mínimo negativo, por uma unidade. Representação binária Decimal Sem sinal Sinal-magnitude Complemento de um Complemento de dois +15 1111 — — — +14 1110 — — — +13 1101 — — — +12 1100 — — — +11 1011 — — — +10 1010 — — — +9 1001 — — — +8 1000 — — — +7 0111 0111 0111 0111 +6 0110 0110 0110 0110 +5 0101 0101 0101 0101 +4 0100 0100 0100 0100 +3 0011 0011 0011 0011 +2 0010 0010 0010 0010 +1 0001 0001 0001 0001 +0 — 0000 0000 — 0 0000 — — 0000 −0 — 1000 1111 — −1 — 1001 1110 1111 −2 — 1010 1101 1110 −3 — 1011 1100 1101 −4 — 1100 1011 1100 −5 — 1101 1010 1011 −6 — 1110 1001 1010 −7 — 1111 1000 1001 −8 — — — 1000 Para obter o número negativo em complemento de um deve-se complementar (inverter) todos os bits do número binário positivo. Para obter o número negativo em complemento de dois deve-se: a) obter o complemento de um (complementar (inverter) todos os bits do número binário positivo ); b) somar 1 ao resultado. Para obter o número negativo em sinal-magnitude é necessário apenas adicionar um bit 1 a esquerda do msb. Note que em todos os casos a representação de números com sinal, sempre implica na necessidade de um bit a mais. 13 (decimal) = 1101 (binário sem sinal) +13 (decimal) = 01101 (binário em sinal-magnitude) -13 (decimal) = 11101 (binário em sinal-magnitude) +13 (decimal) = 01101 (binário em complemento de um) -13 (decimal) = 10010 (binário em complemento de um) +13 (decimal) = 01101 (binário em complemento de dois) -13 (decimal) = 10011 = 10010 + 1 (binário em complemento de dois) PARA O PRÓXIMO ENCONTRO Iniciar a resolução dos Exercícios 1.7 ao 1.49 Capítulo 1 - Projeto Digital e Arquitetura de Computadores Encontro 4 (27 fev) Código ASCII O código ASCII (American Standard Code for Information Interchange), é um padrão de codificação de caracteres para comunicação digital. Ele tem apenas 128 pontos de código, sendo 95 são caracteres imprimíveis e os demais são não imprimíveis (em azul no quadro abaixo), sendo usados para diversos controles de equipamentos eletrônicos. Atualmente esse código está sendo substituido pelos códigos UNICODE, que tem milhões de pontos de código, mas nos UNICODE os primeiros 128 são iguais ao conjunto ASCII. Código ...0000 ...0001 ...0010 ...0011 ...0100 ...0101 ...0110 ...0111 ...1000 ...1001 ...1010 ...1011 ...1100 ...1101 ...1110 ...1111 …0 …1 …2 …3 …4 …5 …6 …7 …8 …9 …A …B …C …D …E …F 000... 0… NUL SOH STX ETX EOT ENQ ACK BEL BS HT LF VT FF CR SO SI 001... 1… DLE DC1 DC2 DC3 DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS US 010... 2… SP ! " # $ % & ' ( ) * + , - . / 011... 3… 0 1 2 3 4 5 6 7 8 9 : ; < = > ? 100... 4… @ A B C D E F G H I J K L M N O 101... 5… P Q R S T U V W X Y Z [ \ ] ^ _ 110... 6… ` a b c d e f g h i j k l m n o 111... 7… p q r s t u v w x y z { } ~ DEL Ver também [https://www.lookuptables.com/text/ascii-table ASCII Lookup Table Exemplo de leitura do quadro acima: A letra "A" é representado pelo número hexadecimal 41, o que corresponde a 01000001 em binário A letra "a" é representado pelo número hexadecimal 61, o que corresponde a 01100001 em binário O espaço "SP" é representado pelo número hexadecimal 20, o que corresponde a 00100000 em binário Descubra o que está escrito neste código binário onde cada 8 bits correspondem a um simbolo ASCII: 01000010 01101111 01101101 00100000 01100100 01101001 01100001 00100000 01110000 01100101 01110011 01110011 01101111 01000001 01001100 01001100 Código UNICODE O Unicode é capaz de representar uma ampla variedade de caracteres, incluindo caracteres alfabéticos, numéricos, símbolos, caracteres especiais e até mesmo caracteres em idiomas e sistemas de escrita complexos, como chinês, árabe, hindi, hebraico, japonês, emojis entre outros. O Unicode possui um espaço de codificação grande o suficiente para suportar milhares de caracteres diferentes. O Unicode é implementado nos esquemas de codificação UTF-8, UTF-16 e UTF-32. O mais utilizado na web é o UTF-8, por ser eficiente em uso de número de bits e ser compatível com o ASCII. Hoje em dia o UTF-8 é usado em 98% de todos os websites conhecidos [1]. Para cobrir uma vasta gama de caracteres, o Unicode os organiza em blocos. Exemplos de blocos: "Latin basic","Greek and Coptic", "Chess Symbols", "Emoticons", "Mayan Numerals", etc. Ver outros em Unicode Characters and Blocks - Lookup Tables Para testar a conversão de texto para o código UTF-8 use utf8 to hexadecimal converter O processo reverso pode ser feito usando hexadecimal to utf8 converter Para obter o codepoint de uma simbolo ou texto utf8 to code points converter O processo reverso pode ser feito usando code points to utf8 converter Outros códigos binários: Gray - É um código em que dois valores consecutivos diferem em apenas um bit. Isso é útil para minimizar erros de leitura em sistemas eletrônicos, já que a transição entre estados ocorre com uma única mudança de bit, facilitando a detecção de erros. Note por exemplo: Em código binário convencional o número adjacente a 0111 (7) é o 1000 (8), mudança em 4 bits. Em código Gray o número adjacente a 0100 (7) é o 1100 (8), mudança de apenas 1 bit. One-hot - Neste código cada valor é representado por uma única posição ativa (ALTO) dentro do conjunto de bits, enquanto todas as outras posições estão inativas (BAIXO). Esse código é frequentemente usado em sistemas digitais para representar estados discretos, como em máquinas de estados finitos, e também na geração de sinais de seleção de múltiplos circuitos tais como memórias. A vantagem principal reside na simplicidade da detecção de um único estado ativo, evitando ambiguidades e permitindo uma implementação eficiente em hardware. Johnson - Neste código é gerado deslocando-se sucessivamente todos os bits para a esquerda e colocando o bit complementar do msb como lsb. A codificação normalmente começa com todos bits "0". Devido a sua simplicidade, ele é utilizado para contadores utilizados em controle de sistemas digitais simples de alta velocidade. Por sempre ter apenas 1 bit de diferença entre números adjacentes, ele fornece boa proteção contra erros, mas necessita de mais bits para representar a mesma faixa de valores que um binário sequencial. BCD (Binary-coded decimal) - Esse código basicamente consiste em representar cada digito decimal de 0 a 9 por um grupo de 4 bits (0 -> 0000, 1 -> 0001, ... 8 -> 1000 e 9 -> 1001). Ele é utilizado em mostradores de sete segmentos, onde cada um deles indica um dígito. Decimal Hexadecimal Octal Binário convencional Binário Gray Binário One Hot Binário Johnson BCD 00 0 00 0000 0000 0000.0000.0000.0001 00000000 0000.0000 01 1 01 0001 0001 0000.0000.0000.0010 10000000 0000.0001 02 2 02 0010 0011 0000.0000.0000.0100 11000000 0000.0010 03 3 03 0011 0010 0000.0000.0000.1000 11100000 0000.0011 04 4 04 0100 0110 0000.0000.0001.0000 11110000 0000.0100 05 5 05 0101 0111 0000.0000.0010.0000 11111000 0000.0101 06 6 06 0110 0101 0000.0000.0100.0000 11111100 0000.0110 07 7 07 0111 0100 0000.0000.1000.0000 11111110 0000.0111 08 8 10 1000 1100 0000.0001.0000.0000 11111111 0000.1000 09 9 11 1001 1101 0000.0010.0000.0000 01111111 0000.1001 10 A 12 1010 1111 0000.0100.0000.0000 00111111 0001.0000 11 B 13 1011 1110 0000.1000.0000.0000 00011111 0001.0001 12 C 14 1100 1010 0001.0000.0000.0000 00001111 0001.0010 13 D 15 1101 1011 0010.0000.0000.0000 00000111 0001.0011 14 E 16 1110 1001 0100.0000.0000.0000 00000011 0001.0100 15 F 17 1111 1000 1000.0000.0000.0000 00000001 0001.0101 Extensão de bits de um número inteiro sem sinal Para estender um número de M bits para N bits, basta adicionar (N-M) zeros à esquerda, de modo a ter N bits no total. Exemplo: Estender o número binário sem sinal de 5 bits "01101" para 8 bits: Número original: 01101 = (13 em decimal), pois 8 + 4 + 1 = 13 Número estendido: 00001101 = (13 em decimal), pois 8 + 4 + 1 = 13 Extensão de bits de um número inteiro com sinal em complemento de 2 Para estender um número de M bits para N bits em complemento de 2, o msb (o bit mais significativo) deve ser estendido (copiado) (N-M) vezes para os novos bits à esquerda, de modo a ter N bits no total. Exemplo: Estender o número binário com sinal em complemento de 2 de 5 bits "10011" para 8 bits: Número original: 10011 = (-13 em decimal), pois -16 + 2 + 1 = -13 Número estendido: 11110011 = (-13 em decimal), pois -128 + 64 + 32 + 16 + 2 + 1 = -13 Note que para números positivos o resultado é similar a estender o número inteiro sem sinal. Extensão de bits de um número inteiro com sinal em sinal-magnitude Para estender um número de M bits para N bits do tipo sinal-magnitude, o msb (o bit mais significativo) deve ser movido para o novo msb, e os demais novos bits devem ser zerados. Exemplo: Estender o número binário com sinal em sinal-magnitude de 5 bits "10011" para 8 bits: Número original: 11101 = (-13 em decimal), pois -(+8 + 4 + 1) = -13 Número estendido: 10001101 = (-13 em decimal), pois -(+8 + 4 + 1) = -13 Números binário fracionários em Ponto Fixo A representaçaõ de Ponto Fixo é um número binário que permite representares números fracionários. Os valores são todos escalonados por um fator constante para transformar em um número inteiro. Assim, o número 5,25 pode ser escalonado por 2² => 5,25 x 4 = 21, e portanto 5,25 = 21 / 2². Assim, usando dois bits fracionarios, o número 5,25 pode ser escrito em binário como 10101, onde o separador fracionário esta em 101,01. Usando $M$ bits para representar um número de ponto fixo Q(M,F) com F bits fracionários, é possível representar números fracionários no intervalo de $[0,2^{M-F}-2^{-F}]$. Neste caso a resolução (menor quantidade que se pode representar) é de $2^{-F}$ Por exemplo usando Q(8,3) => $[0;2^{5}-2^{-3}]=[0;31,875]=[00000,000_{2};11111,111_{2}]$, e a resolução é de $2^{-3}=0,125$. bit 4 3 2 1 0 -1 -2 -3 valor 1 0 1 0 0 1 1 1 peso 24 23 22 21 20 2-1 2-2 2-3 peso +16 +8 +4 +2 +1 +0,5 +0,25 +0,125 somar +16 +4 +0,5 +0,25 +0,125 resultado 16 + 4 + 0,5 + 0,25 + 0,125 = 20,875 Note que que é possível obter rapidamente o valor de um número de ponto fixo, obtendo o valor do seu número inteiro correspondente, dividindo-o por 2-F. No exemplo acima, 10100111, corresponde ao inteiro 167, ou seja se o número é do tipo Q(8,3), o valor é de 167/2-F = 20,875. Assim como nos números inteiros, é possível representar também números em ponto fixo negativos usando complemento de 2 ou sinal-magnitude. PARA O PRÓXIMO ENCONTRO Resolução dos Exercícios 1.7 ao 1.49 Capítulo 1 - Projeto Digital e Arquitetura de Computadores Ler Capítulo 2 - Representações Binárias em Eletrônica digital moderna e VHDL / Volnei A. 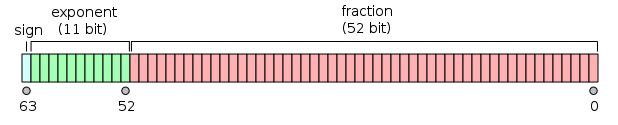Pedroni; tradução de Arlete Simille Marques Ver exercícios 2.2 a 2.13, 2.16 a 2.18, 2.21 a 2.26, 2.29 a 2.32, 2.39 a 2.41 de [2] Encontro 5 (29 fev) Ponto Flutuante (floating point) Os números de ponto flutuante são agrupados da esquerda para a direita:1) bit de sinal, 2) expoente e 3) mantissa. Para os formatos binários IEEE 754 (básico e estendido) que possuem implementações de hardware existentes, eles são distribuídos da seguinte forma: Tipo Sinal Exponente Mantissa Total bits   Viés do exponente Precisão em bits Half-precision 1 5 10 16   15 11 Single-precision 1 8 23 32   127 24 Double-precision 1 11 52 64   1023 53 Embora o expoente possa ser positivo ou negativo, em formatos binários ele é armazenado como um número sem sinal que possui um "viés" fixo adicionado a ele. A faixa de expoente para números normais é [−126, 127] para precisão simples, [−1022, 1023] para dupla. Existem três tipos principais de números: normalizados, denormalizados (ou desnormalizados) e especiais (como infinito e NaN - "Not a Number"). Nos formatos IEEE, o bit 1 inicial de um significando normalizado não é realmente armazenado. É chamado de bit "oculto" ou "implícito". Por causa disso, o formato de precisão simples na verdade tem um significando com 24 bits de precisão, o formato de precisão dupla tem 53. O layout para o ponto flutuante de 32 bits e de 64 bits são mostrados abaixo: Como converter de decimal para floating point? Identifique quantos bits serão usados e obtenha o viés (veja na tabela acima) Converta o número decimal para binário ponto fixo: Normalize a mantissa, movendo o ponto decimal para que haja apenas um um dígito à esquerda do ponto decimal. Determine o sinal, o expoente e a mantissa: 1) O número é positivo, então o bit de sinal é 0. 2) O expoente é o deslocamento necessário para normalizar a mantissa. 3) A mantissa é a parte fracionária normalizada. Converta o expoente para binário com bias: Adicionamos o viés ao expoente para obter o valor final. Junte os bits na ordem: sinal, expoente e mantissa, e obtenha o número em IEEE 754 Floating Point Exemplo: Dado o número 85,125 converta para a representação floating point de 32 bits P1: 32 bits, portanto o viés é 127. P2: 85 em binário é 1010101. 0.125 em binário é 0.001. Portanto, 85,125 em binário é 1010101.001 P3: 1010101.001 => 1.010101001 × 2^6 P4: O número é positivo, então o bit de sinal é 0. O expoente é o deslocamento necessário para normalizar a mantissa. No caso, 6. A mantissa é a parte fracionária normalizada, que é 010101001.(note que o 1 a esquerda do ponto decimal não será representado. P5: Expoente = 6 + 127 = 133 em binário é 10000101. P6: Sinal: 0, Expoente: 10000101, Mantissa: 01010100100000000000000 (completar com zeros até 23 bits), portanto 0 10000101 01010100100000000000000 FONTE: How to Convert a Number from Decimal to IEEE 754 Floating Point Representation Como converter de floating point para decimal? Identifique o número de bits e obtenha o número de bits do expoente e o viés (veja na tabela acima), Obtenha o sinal do número a partir do msb (S = 0 => +; S = 1 => -) Obtenha o número correspondente ao Expoente (E). Considerando o viés, calcule o expoente (e = E - viés) Obtenha o valor da mantissa (M) e Obtenha o valor decimal correspondente, acrescentando o 1 inteiro (se o numero estiver normalizado) antes da conversão O resultado em decimal é $(-)^{S}\times 1.M\times 2^{E-vies}$ Exemplo: Dado o número representado em floating point de 32 bits = 11000000111000000000000000000000 P1: Expoente tem 8 bits => viés = 127 (28-1-1) P2: Sinal (msb): 1 => é um número negativo (-) P3: Expoente (8 bits): 10000001 = 129 P4: expoente (e = E - vies) 129 - 127 = 2 P5: Mantissa: (23 bits): 11000000000000000000000 P6: Valor (24 bits):1.11000000000000000000000 = 1,75 P7: Resultado: (-) 1,75 x 22 = -7 Números sub_normais Os números sub_normais são indicados pelo Expoente = 00000000. Esse Expoente será interpretado como 2-126. Eles, ao contrário dos números normalizados, não usam um "1" implícito no início da mantissa. Isso significa que a mantissa desses números começa com um "0" explícito antes da parte fracionária, permitindo representar valores muito pequenos que não podem ser normalizados devido à limitação dos bits do expoente. Exemplos: 0 00000000 00000000000000000000000 corresponde ao número +0 1 00000000 00000000000000000000000 corresponde ao número -0 0 00000000 10000000000000000000000 corresponde ao número 0,5 x 2-126 = 5.877472E-39 1 00000000 00000000000000000000001 corresponde ao número -2-23 x 2-126 = -0.00000011920928955078125 x 2-126 = -1.40129846432481707092373E-45 (2-149 Números especiais Infinito Positivo (Inf): Bit de sinal: 0 (positivo) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Todos os bits definidos como 0 (23 bits) Representação em 32 bits: 0 11111111 00000000000000000000000 Infinito Negativo (-Inf): Bit de sinal: 1 (negativo) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Todos os bits definidos como 0 (23 bits) Representação em 32 bits: 1 11111111 00000000000000000000000 NaN (Not a Number): Bit de sinal: Pode ser 0 ou 1 (geralmente usado para sinalizar erros ou operações indefinidas) Expoente: Todos os bits definidos como 1 (8 bits) Mantissa: Pelo menos um bit não nulo (23 bits) Representação: x 11111111 yyyyyyyyyyyyyyyyyyyyyyy (onde "x" é o bit de sinal e "y" são bits da mantissa) Exemplos de conversores online IEEE 754 Calculator 16-bits & 32-bits & 64-bits & 128-bits IEEE-754 Floating Point Converter 32-bitsVer Ponto Fixo e Flutuante - prof. Odilson Ver Floating-point arithmetic - wikipedia Ver IEEE 754 - wikipedia Ler sobre os hardware de microprocessadores [3]. Para ver o número de bits de cada arquitetura, clique no link correspondente na tabela.|} Unidade 3 - Funções, portas lógicas e álgebra booleana 10 ENCONTROS Unidade 3 - Funções, portas lógicas e álgebra booleana Encontro 6 (5 mar.) Funções e portas lógicas Funções e portas lógicas PARA O PRÓXIMO ENCONTRO Rever Funções e portas lógicas Ler pag 49 a 69 de Projeto Digital e Arquitetura de Computadores Encontro 7 (7 mar.) Funções e portas lógicas Funções e portas lógicas PARA O PRÓXIMO ENCONTRO Como as portas lógicas são implementadas com transistores CMOS Encontro 8 (12 mar.) Álgebra de Boole - slides PARA O PRÓXIMO ENCONTRO Rever slides 1 a 15 de Álgebra de Boole Ler a seção 2.3.ÁLGEBRA BOOLEANA nas pag 107 a 116 de Projeto Digital e Arquitetura de Computadores Ler a seção 4-2 LEIS E REGRAS DA ÁLGEBRA BOOLEANA nas pag 201 a 206 de FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 na Minha Biblioteca Encontro 9 (14 mar.) Álgebra de Boole Teoremas de De Morgan O complemento do produto é igual a soma dos complementos: ${\overline {X\cdot Y}}={\overline {X}}+{\overline {Y}}$ O complemento da soma é igual ao produto dos complementos: ${\overline {X+Y}}={\overline {X}}\cdot {\overline {Y}}$ Para provar os teoremas, podemos obter a tabela verdade de ambos lados de cada equação booleana. Entradas Saídas X Y ${\overline {X\cdot Y}}$ ${\overline {X}}+{\overline {Y}}$ 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 0 Entradas Saídas X Y ${\overline {X+Y}}$ ${\overline {X}}\cdot {\overline {Y}}$ 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 0 Ou utilizar os postulados e teoremas da algebra de boole. Considerando que ${\overline {X+Y}}={\overline {X}}\cdot {\overline {Y}}$ seja verdade, então PASSO 1: pelo postulado do complemento ${\overline {A}}+A=1$, podemos afirmar que $(X+Y)+({\overline {X}}\cdot {\overline {Y}})=1$ PASSO 2: pelo teorema da distribuição $A+(B\cdot C)=(A+B)\cdot (A+C)$, podemos afirmar que $(X+Y)+({\overline {X}}\cdot {\overline {Y}})=(X+Y+{\overline {X}})\cdot (X+Y+{\overline {Y}})$ PASSO 3: pelo teorema da comutação $A+B=B+A$, podemos afirmar que $(X+Y+{\overline {X}})\cdot (X+Y+{\overline {Y}})=(Y+X+{\overline {X}})\cdot (X+Y+{\overline {Y}})$ PASSO 4: pelo postulado do complemento $A+{\overline {A}}=1$, podemos afirmar que $(Y+X+{\overline {X}})\cdot (X+Y+{\overline {Y}})=(Y+1)\cdot (X+1)$ PASSO 5: pelo postulado do elemento absorvente $A+1=1$, podemos afirmar que $(Y+1)\cdot (X+1)=1\cdot 1$ PASSO 6: pelo postulado da multiplicação (AND) $1\cdot 1=1$, podemos afirmar que $1\cdot 1=1$ Portanto a consideração inicial é verdadeira ${\overline {X+Y}}={\overline {X}}\cdot {\overline {Y}}$. Nota: O teorema também pode ser provado usando o postulado do complemento ${\overline {A}}\cdot A=0$, pois neste caso, podemos afirmar que $(X+Y).({\overline {X}}\cdot {\overline {Y}})=0$. Tente desenvolver o restante da prova usando apenas os postulados e teoremas. Os teoremas de De Morgam são validos para qualquer número (N) de entradas, podem ser escritos como: ${\overline {X_{1}\cdot X_{2}\cdot ...\cdot X_{N}}}={\overline {X_{1}}}+{\overline {X_{2}}}+...+{\overline {X_{N}}}$ ${\overline {X_{1}+X_{2}+...+X_{N}}}={\overline {X_{1}}}\cdot {\overline {X_{2}}}\cdot ...\cdot {\overline {X_{N}}}$ Exercícios Simplifique as expressões lógicas (caso seja possível). Indique os Postulados ou Teoremas utilizado em cada passo. Para simplificar as notações os códigos A1 a A5 e T1 a T12 ou T1' a T12' indicado na Folha de consulta - álgebra booleana. a) ABC + A + BC b) A.B + A.B’ + A’.B c) X.Y + X.Y’ + X’.Y + X.Y d) X.Y + X.Z + Z.Y e) D.B’+D.(D.B+C.D’) Ver também exemplos em 4-4 ANÁLISE BOOLEANA DE CIRCUITOS LÓGICOS [FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 PARA O PRÓXIMO ENCONTRO Rever slides 16 até fim de Álgebra de Boole Ler a seção 2.3.ÁLGEBRA BOOLEANA nas pag 107 a 116 de Projeto Digital e Arquitetura de Computadores Ler a seção 4-3 TEOREMAS DE DEMORGAN e 4-4 ANÁLISE BOOLEANA DE CIRCUITOS LÓGICOS nas pag 207 a 216 de FLOYD, Thomas. Sistemas digitais. Grupo A, 2011. E-book. ISBN 9788577801077 na Minha Biblioteca ATUAL Encontro 10 (21 mar.) Expressão booleana - Tabela verdade - Circuito com portas lógicas: Ver resumo em Expressão booleana - Tabela verdade - Circuito com portas lógicas Ler a seção 2.4. DA LÓGICA ÀS PORTAS e 2.5.LÓGICA COMBINATÓRIO MULTI-NÍVEL nas pag 90 a 95 de Projeto Digital e Arquitetura de Computadores Ver resumo em Exercícios de álgebra de Boole Ler a seção 2.3.4. A Verdade por Detrás de Tudo e 2.3.5. Simplificando Equações nas pag 87 a 90 de Projeto Digital e Arquitetura de Computadores Unidade 4 - Introdução a linguagem VHDL e Quartus/ModelSim 6 ENCONTROS Unidade 4 - Introdução a linguagem VHDL e Quartus/ModelSim Unidade 5 - Circuitos lógicos combinacionais (com VHDL) 12 ENCONTROS Unidade 5 - Circuitos lógicos combinacionais (com VHDL) Unidade 6 - Circuitos aritméticos (com VHDL) 5 ENCONTROS Unidade 6 - Circuitos aritméticos (com VHDL) Avaliações Durante o semestre serão realizadas 4 avaliações. As avaliações devem ser enviadas pela plataforma Moodle com os arquivos solicitados. Data das avaliações A1 - : 05/03 - 1ª parte A1a (3 pontos) (Sistema de Numeração e códigos); A2 - : R - Recuperação de A1 a A2 : Atividade relâmpago (AR) As atividades relâmpago devem ser entregues no Moodle da disciplina. A não entrega dessas atividades não gera nenhum desconto, apenas geram pontos de BÔNUS que são adicionados aos conceitos das avaliações A1 a AN. Atividade extra-classe (AE) A média ponderada das atividades extra-classe será considerada no cálculo do conceito final da UC. A entrega das mesmas será feita pelo Moodle, e cada dia de atraso irá descontar 0,2 na nota da atividade. Muitas dessas atividades também geram pontos de BÔNUS que são adicionados aos conceitos das avaliações A1 a AN. Para os BÔNUS só serão considerados projetos entregues no prazo. Referências Bibliográficas: Curso de Engenharia de Telecomunicações