Mudanças entre as edições de "Conectando uma fonte, condições de contorno"
(Criou página com '== Conectando uma Fonte == Podemos considerar uma linha de transmissão como o elemento que liga uma fonte de tensão ou corrente (gerador, transmissor, antena, ...) à uma car...') |
|||
| (10 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 3: | Linha 3: | ||
Podemos considerar uma linha de transmissão como o elemento que liga uma fonte de tensão ou corrente (gerador, transmissor, antena, ...) à uma carga (impedância, receptor, antena, ...). Quando analisamos o terminal "final" da linha, modelamos a carga por seu impedância de entrada. Não precisamos de mais informações da carga para analisar a tensão e a corrente na linha. | Podemos considerar uma linha de transmissão como o elemento que liga uma fonte de tensão ou corrente (gerador, transmissor, antena, ...) à uma carga (impedância, receptor, antena, ...). Quando analisamos o terminal "final" da linha, modelamos a carga por seu impedância de entrada. Não precisamos de mais informações da carga para analisar a tensão e a corrente na linha. | ||
| + | |||
| + | Em relação a fonte, para análise da linha de transmissão, modelamos a mesma pelo seu circuito equivalente de Thevenin ou Norton. | ||
| + | |||
| + | figura 1: circuitos de Thevenin e Norton | ||
| + | [[Arquivo:Thevenin.png]] [[Arquivo:Norton.png]] | ||
| + | |||
| + | |||
| + | |||
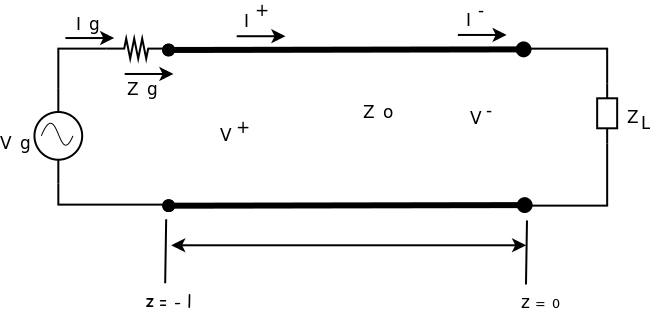
| + | Utilizando Thevenin o circuito completo da linha com fonte e carga passa a ser: | ||
| + | |||
| + | figura 2: circuito completo | ||
| + | [[Arquivo:Circuito completo.png]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Do circuito completo obtemos as relações: | ||
| + | |||
| + | ::::<math>V_i= V(z=-l)</math> (1) | ||
| + | |||
| + | ::::<math>V(z=-l) = {V_g . Z_{in} \over Z_g + Z_{in}}</math> (2) | ||
| + | |||
| + | |||
| + | de (1) temos: | ||
| + | |||
| + | ::::<math>V(z=-l) = V_o^+ e^{j\beta l} + \Gamma_L V_o^+ e^{-j\beta\ l})</math> (3) | ||
| + | |||
| + | |||
| + | lembrando que <math> \Gamma_{in} = \Gamma_L e^{j2\beta l}</math> podemos substituir <math>\Gamma_L</math> na equação (3): | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>V(z=-l) = V_o^+ e^{j\beta l} + {\Gamma_{in} V_o^+ e^{-j\beta l}\over e^{j2\beta l}} </math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>V(z=-l) = V_o^+ e^{j\beta l} ( 1 + \Gamma_{in})</math> (4) | ||
| + | |||
| + | |||
| + | como: | ||
| + | |||
| + | ::::<math>\Gamma_{in} = { Z_{in} - Z_o \over Z_{in} + Z_o}</math> | ||
| + | |||
| + | |||
| + | podemos escrever Z_{in} como: | ||
| + | |||
| + | |||
| + | ::::<math>Z_{in} = {-Z_o (\Gamma_{in} + 1) \over (\Gamma_{in} - 1)} </math> (5) | ||
| + | |||
| + | |||
| + | substituindo (4) e (5) em (2): | ||
| + | |||
| + | ::::<math>V_o^+ e^{j\beta l} ( 1 + \Gamma_{in}) = V_g {{-Z_o (\Gamma_{in} + 1) \over (\Gamma_{in} - 1)} \over Z_g + {-Z_o (\Gamma_{in} + 1) \over (\Gamma_{in} - 1)}}</math> | ||
| + | |||
| + | |||
| + | ::::<math>V_o^+ e^{j\beta l} ( 1 + \Gamma_{in}) = V_g {-Z_o (\Gamma_{in} + 1) \over Z_g (\Gamma_{in} - 1) + -Z_o (\Gamma_{in} + 1)}</math> | ||
| + | |||
| + | |||
| + | ::::<math>V_o^+ = V_g e^{-j\beta l} {-Z_o \over -Z_o (\Gamma_{in} + 1) + Z_g (\Gamma_{in} - 1)}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>V_o^+ = V_g e^{-j\beta l} {Z_o \over Z_o (\Gamma_{in} + 1)+ Z_g (1 - \Gamma_{in})}</math>(6) | ||
| + | |} | ||
| + | |||
| + | |||
| + | A equação (6) mostra a relação de <math>V_o^+</math> com a fonte (<math>V_g</math> e <math>Z_g</math>), com a linha (Z<math>_o</math> e l) e com a carga, pois <math>\Gamma_{in}</math> é dependente de <math>Z_L</math>. Neste equacionamento também é indicado que a tensão incidente da linha depende da fonte e da carga! | ||
| + | |||
| + | Como <math>V_o^-</math> também depende de <math>V_o^+</math>, as duas ondas de tensão, incidente e refletida, são dependentes da fonte e da carga. Isto é, somente conhecendo as condições de contorno (fonte e carga) é que podemos definir <math>V_o^+</math> e <math>V_o^-</math>. | ||
Edição atual tal como às 12h29min de 3 de novembro de 2015
Conectando uma Fonte
Podemos considerar uma linha de transmissão como o elemento que liga uma fonte de tensão ou corrente (gerador, transmissor, antena, ...) à uma carga (impedância, receptor, antena, ...). Quando analisamos o terminal "final" da linha, modelamos a carga por seu impedância de entrada. Não precisamos de mais informações da carga para analisar a tensão e a corrente na linha.
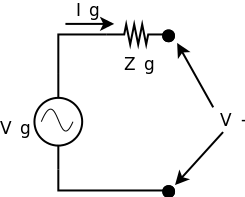
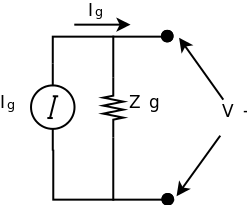
Em relação a fonte, para análise da linha de transmissão, modelamos a mesma pelo seu circuito equivalente de Thevenin ou Norton.
figura 1: circuitos de Thevenin e Norton
Utilizando Thevenin o circuito completo da linha com fonte e carga passa a ser:
Do circuito completo obtemos as relações:
- (1)
- (2)
de (1) temos:
- (3)
lembrando que podemos substituir na equação (3):
- (4)
como:
podemos escrever Z_{in} como:
- (5)
substituindo (4) e (5) em (2):
| (6) |
A equação (6) mostra a relação de com a fonte ( e ), com a linha (Z e l) e com a carga, pois é dependente de . Neste equacionamento também é indicado que a tensão incidente da linha depende da fonte e da carga!
Como também depende de , as duas ondas de tensão, incidente e refletida, são dependentes da fonte e da carga. Isto é, somente conhecendo as condições de contorno (fonte e carga) é que podemos definir e .