Mudanças entre as edições de "Coeficiente de reflexão, Impedância de entrada e Potência"
| (58 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
| + | == Coeficiente de reflexão == | ||
| + | |||
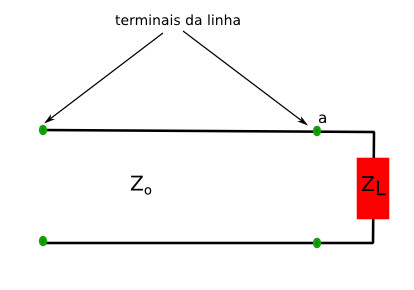
Uma linha de transmissão possui uma impedância característica '''Zo''' definida pela relação entre a''' <math>V^+</math> e <math>I^+</math>'''. Considere que uma carga '''<math>Z_L</math>''' é acoplada a um dos terminais da linha (figura 1). | Uma linha de transmissão possui uma impedância característica '''Zo''' definida pela relação entre a''' <math>V^+</math> e <math>I^+</math>'''. Considere que uma carga '''<math>Z_L</math>''' é acoplada a um dos terminais da linha (figura 1). | ||
| Linha 7: | Linha 9: | ||
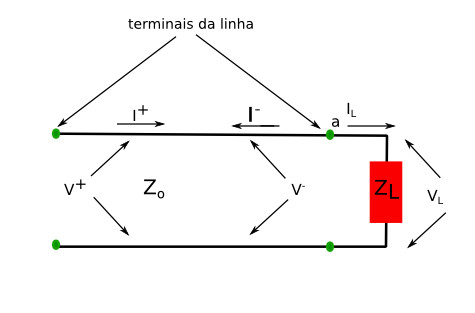
| − | Sobre essa carga teremos uma tensão <math>V_L</math>, fazendo circular uma corrente <math>I_L</math>. Na linha teremos as tensões <math>V^+</math> e <math>V^-</math> e as correntes <math>I^+</math> e <math>I^-</math>, conforme indicado no figura 2. | + | Sobre essa carga teremos uma tensão <math>V_L</math>, fazendo circular uma corrente <math>I_L</math>. Na linha teremos as tensões <math>V^+</math> e <math>V^-</math> e as correntes <math>I^+</math> e <math> I^-</math>, conforme indicado no figura 2. |
| − | figura 2: | + | figura 2: Linha com carga com tensões e correntes. |
[[Arquivo:Linha_com_tensoes.jpg]] | [[Arquivo:Linha_com_tensoes.jpg]] | ||
| Linha 18: | Linha 20: | ||
| − | ::::<math>Z_L = {V_L \over I_L}</math> | + | ::::<math>\ Z_L = {V_L \over I_L}</math> |
| Linha 24: | Linha 26: | ||
| − | ::::<math>V_L = | + | ::::<math>\ V_L = V_o^+e^{-\gamma z} + V_o^-e^{\gamma z} </math> |
| Linha 31: | Linha 33: | ||
| − | ::::<math>I_L = | + | ::::<math>\ I_L = I_o^+e^{-\gamma z} + I_o^-e^{\gamma z}</math> |
| Linha 37: | Linha 39: | ||
| − | ::::<math>Z_L = { | + | ::::<math>\ Z_L = {V_o^+ + V_o^-\over I_o^+ + I_o^-}</math> |
| − | como, | + | como em z= 0, |
| − | ::::<math>Z_o = { | + | ::::<math>\ Z_o = {V_o^+\over I_o^+ }= {-V_o^-\over I_o^- }</math> |
| Linha 49: | Linha 51: | ||
| − | ::::<math>Z_L = { | + | ::::<math>\ Z_L = {V_o^+ + V_o^-\over{{V_o^+ \over Z_o} -{ V_o^- \over Z_o}}}</math> |
| Linha 55: | Linha 57: | ||
| − | ::::<math> { | + | ::::<math>\ {V_o^- \over V_o^+} = {Z_L - Z_o \over Z_L + Z_o}</math> |
| Linha 64: | Linha 66: | ||
{| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | {| class="wikitable" style="margin: auto;color:red; background-color:#ffffcc;" cellpadding="10" | ||
| − | |<math>\Gamma _L = {Z_L - Z_o \over Z_L + Z_o}</math> | + | |<math>\ \Gamma _L = {Z_L - Z_o \over Z_L + Z_o}</math> |
|} | |} | ||
| + | == coeficiente de reflexão afastado da carga == | ||
| + | |||
| + | |||
| + | O valor de Γ em qualquer ponto da linha será dado pela relação entre <math>{V^+ \over V^-}</math>, sendo assim para um ponto afastado uma distância '''<math>l</math>''' da carga teremos: | ||
| − | |||
| + | :::: <math>\ \Gamma_{in} = \Gamma (z) = { V_o^- e^{\gamma z} \over V_o^+ e^{-\gamma z}} = \Gamma_L e^{2\gamma z}</math> | ||
| − | |||
| + | considerando um deslocamento '''<math>l</math>''' a partir da carga (z=0) para a esquerda (sentido -z) temos: | ||
| − | |||
{| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| − | |<math>\ | + | |<math>\ \Gamma_{in} = \Gamma _L e^{-2\gamma l} (1)</math> |
|} | |} | ||
| Linha 88: | Linha 93: | ||
| − | [[Arquivo: | + | [[Arquivo:Impedancia_de_entrada.gif]] |
| + | Observe que <math>Z_in</math> é dada em função de <math>-l</math> | ||
| − | + | '''não estamos nos referindo a '''Zo''' (impedância característica) esta corresponde a relação''' <math> {V^+ \over I^+}</math>''', enquanto que '''Zin''' é dada por: | |
| − | ::::<math>Z_{in( | + | ::::<math>\ Z_{in(-l)}= { V_o^+ e^{\gamma l} + V_o^- e^{-\gamma l} \over I_o^+ e^{\gamma l} + I_o^- e^{-\gamma l}}</math> |
| − | substituindo <math>I_o^+ </math> e <math>I_o^ | + | substituindo <math>I_o^+ </math> e <math>I_o^- </math> por: |
| − | ::::<math>I_o^+= {V_o^+ \over Z_o} </math> | + | ::::<math>\ I_o^+= {V_o^+ \over Z_o} </math> |
| − | ::::<math>I_o^-= {-V_o^- \over Z_o} </math> | + | ::::<math>\ I_o^-= {-V_o^- \over Z_o} </math> |
| Linha 109: | Linha 115: | ||
| − | ::::<math>Z_{in(z)}= Z_o { V_o^+ e^{ | + | ::::<math>\ Z_{in(z)}= Z_o { V_o^+ e^{\gamma z} + V_o^- e^{-\gamma z} \over V_o^+ e^{\gamma z} - V_o^- e^{-\gamma z}}</math> |
| − | agora substituindo <math>V_o^- = \ | + | agora substituindo <math>V_o^- = \Gamma_L V_o^+</math>: |
| − | ::::<math>Z_{in(z)}= Z_o { V_o^+ e^{ | + | ::::<math>\ Z_{in(z)}= Z_o { V_o^+ e^{\gamma z} + \Gamma_L V_o^+ e^{-\gamma z} \over V_o^+ e^{\gamma z} - \Gamma_L V_o^+ e^{-\gamma z}}</math> |
| − | ::::<math>Z_{in(z)}= Z_o {e^{ | + | ::::<math>\ Z_{in(z)}= Z_o {e^{\gamma z} + \Gamma_L e^{-\gamma z} \over e^{\gamma z} - \Gamma_L e^{-\gamma z}}</math> |
| − | ::::<math>Z_{in(z)}= Z_o { e^{ | + | ::::<math>\ Z_{in(z)}= Z_o { e^{\gamma z} + {(Z_L -Z_o) \over (Z_L + Z_o)} e^{-\gamma z} \over e^{\gamma z} - {(Z_L -Z_o) \over (Z_L + Z_o)} e^{-\gamma z}}</math> |
| − | ::::<math>Z_{in(z)}= Z_o { Z_L (e^{ | + | ::::<math>\ Z_{in(z)}= Z_o { Z_L (e^{\gamma z} + e^{-\gamma z}) + Z_o(e^{\gamma z} - e^{-\gamma z}) \over Z_L (e^{\gamma z} - e^{-\gamma z}) + Z_o (e^{\gamma z} + e^{-\gamma z})}</math> |
| − | dividindo numerador e denominador por <math>e^{ | + | dividindo numerador e denominador por <math>e^{\gamma z} + e^{-\gamma z}</math> e lembrando que: |
| − | <math>\tanh {e^ | + | ::::<math>\ \tanh x= {e^x - e^{-x} \over e^x + e^{-x}} </math> |
| Linha 140: | Linha 146: | ||
{| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| − | |<math>Z_{in(z)}= Z_o {Z_L + Z_o tanh \gamma z \over Z_o + Z_L tanh \gamma z}</math> | + | |<math>\ Z_{in(z)}= Z_o {Z_L + Z_o tanh \gamma z \over Z_o + Z_L tanh \gamma z} (2)</math> |
| + | |} | ||
| + | |||
| + | == Potência incidente, entregue à carga e refletida == | ||
| + | |||
| + | === Potência incidente === | ||
| + | Ao conectar uma fonte em uma linha de transmissão, passa a se propagar pela linha uma onda de tensão e outra de corrente. Essas duas ondas transportam energia elétrica (figura 1). | ||
| + | |||
| + | Figura 4: linha percorrida por onda de tensão e corrente que transmitem potência elétrica. | ||
| + | |||
| + | [[Arquivo:Potencia_incidente.jpg]] | ||
| + | |||
| + | Se a fonte de tensão for harmônica, cossenoidal por exemplo, podemos calcular a potência média ativa transmitida por: | ||
| + | |||
| + | |||
| + | ::::<math>\ P^+(l) = {1 \over 2} \Re \{V(l)^+.I(l)^{+*} \}</math> (3) | ||
| + | |||
| + | |||
| + | ::::<math>\ V(l)^+</math> e <math>I(l)^+</math> são dados por: | ||
| + | |||
| + | |||
| + | ::::<math>\ V(l)^+ = V_o^+ e^{-\alpha l} e^{-j\beta l} </math> (4) | ||
| + | |||
| + | |||
| + | ::::<math>\ I(l)^+ = I_o^+ e^{-\alpha l} e^{j\theta} e^{-j\beta l} </math> (5) | ||
| + | |||
| + | |||
| + | O termo <math>e^{j\theta}</math> na equação (5) corresponde ao ângulo de defasagem entre a tensão e a corrente na linha. | ||
| + | |||
| + | Substituindo (4) e (5) em (3) e lembrando que <math>|Z_o| = {V(z)^+ \over I(z)^+}</math>: | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P^+(l) = {1 \over 2} \Re \{ V_o^+ e^{-\alpha l} e^{-j\beta l} . I_o^+ e^{-\alpha l} e^{-j\theta} e^{j\beta l}\}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P^+(l) = {1 \over 2} \Re \{ V_o^+ e^{-\alpha l} e^{-j\beta l} . {V_o^+ \over Z_o} e^{-\alpha l} e^{-j\theta} e^{j\beta l}\}</math> | ||
| + | |||
| + | |||
| + | ::::<math>\ P^+(l) = {1 \over 2} \Re \{ {V_o^{+2} \over |Zo|} e^{-2\alpha l} e^{-j\theta}\}</math> | ||
| + | |||
| + | |||
| + | o que pode ser escrito como: | ||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>\ P^+(z) = {1 \over 2} {V_o^{+2} \over |Z_o|} e^{-2\alpha l} \cos \theta</math> (7) | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | A equação (7) representa a potência transmitida na linha ou potência incidente. Note que a constante α representa a constante de atenuação da linha. | ||
| + | |||
| + | === Potência entregue à carga === | ||
| + | |||
| + | |||
| + | A potência ativa entregue à carga pela linha (<math>P_L</math>) pode ser calculada por: | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{V_L . I_L^*\}</math> | ||
| + | |||
| + | |||
| + | Que pode ser reescrita em função das tensões e correntes no terminal '''a''' da linha de transmissão. | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{V(z) . I(z)^*\}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{(V_o^+ e^{-\alpha z} e^{-j\beta z} + V_o^- e^{\alpha z} e^{j\beta z}) . (I_o^+ e^{-\alpha z} e^{j\theta} e^{j\beta z} + I_o^- e^{\alpha z} e^{j\theta} e^{-j\beta z})\}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{(V_o^+ e^{-\alpha z} e^{-j\beta z} + \Gamma V_o^+ e^{\alpha z} e^{j\beta z}) . ({V_o^+ \over Z_o} e^{-\alpha z} e^{j\theta} e^{j\beta z} + -\Gamma{V_o^+ \over Z_o} e^{\alpha z} e^{j\theta} e^{-j\beta z})\}</math> | ||
| + | |||
| + | |||
| + | Considerando o terminal '''a''' como o ponto onde z=0: | ||
| + | |||
| + | ::::<math>\ P_L = \Re \{(V_o^+ + \Gamma V_o^+) . ({V_o^+ \over Z_o}e^{j\theta} - \Gamma {V_o^+ \over Z_o} e^{j\theta} )\}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{{V_o^{+2} \over Z_o}e^{j\theta} - \Gamma^2 {V_o^{+2} \over Z_o} e^{j\theta} \}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ::::<math>\ P_L = \Re \{{V_o^{+2} \over Z_o}e^{j\theta} (1 - \Gamma^2) \}</math> | ||
| + | |||
| + | |||
| + | |||
| + | o termo <math>\ \Re \{{V_o^{+2} \over Z_o}e^{j\theta}\}</math> é exatamente a potência incidente no terminal '''a''' portanto: | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>\ P_L = P^{+'} (1 - \Gamma^2) </math> (8) | ||
|} | |} | ||
| − | == Potência | + | |
| + | |||
| + | A linha em <math>P^{+'}</math> na equação (8) representa que o cálculo de <math>P_L</math> deve ser realizado descontando a atenuação da linha, isto é utilizando o valor de <math>P(z)^{+}</math> no terminal '''a'''. | ||
| + | |||
| + | === Potência Refletida === | ||
| + | |||
| + | |||
| + | Manipulando um pouco a equação (8) podemos encontrar o relação entre a potência incidente, a potência refletida e a potência entregue à carga: | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = P^{+'} (1 - \Gamma^2) </math> | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = P^{+'} - \Gamma^2 P^{+'} </math> | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = {V^{+'2} \over Z_o} - \Gamma^2 {V^{+'2} \over Z_o} </math> | ||
| + | |||
| + | |||
| + | ::::<math>\ P_L = {V^{+'2} \over Z_o} - {(\Gamma .V^{+'})^2 \over Z_o} </math> | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| + | |<math>\ P_L = {V^{+'2} \over Z_o} - {V_o^{-'2} \over Z_o} </math> (9) | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | O primeiro termo do lado direito da equação (9) corresponde a potência incidente no terminal '''a''' e o segundo termo a potência refletida no mesmo terminal. Esta relação mostra que a parcela de potência que chega ao final da linha e não é absorvida pela carga, retorno para linha. Isto é,<math>\ V^-(z)</math> e <math>\ I^-(z)</math> são as ondas refletidas na linha e transportam a potência refletida. | ||
| + | |||
| + | |||
| + | ==== Potências na linha e entregue à carga ==== | ||
| + | |||
| + | |||
| + | {| class="wikitable" style="margin: auto;color:black; background-color:#ffffcc;" cellpadding="10" | ||
| + | ||Potência incidente||<math>\ P^+(l) = {V^{+'2} \over Z_o} e^{-2\gamma l} cos \theta </math> | ||
| + | |- | ||
| + | ||Potência refletida ||<math>\ P^-(l) = {V^{-'2} \over Z_o} e^{-2\gamma l} cos \theta </math> | ||
| + | |- | ||
| + | ||Potência entregue à carga||<math>\ P_L = {V^{+'2} \over Z_o} - {V_o^{-2} \over Z_o} </math> | ||
| + | |} | ||
Edição atual tal como às 08h08min de 11 de novembro de 2015
Coeficiente de reflexão
Uma linha de transmissão possui uma impedância característica Zo definida pela relação entre a e . Considere que uma carga é acoplada a um dos terminais da linha (figura 1).
figura 1: Linha com carga
Sobre essa carga teremos uma tensão , fazendo circular uma corrente . Na linha teremos as tensões e e as correntes e , conforme indicado no figura 2.
figura 2: Linha com carga com tensões e correntes.
Podemos escrever como:
Mas no nó terminal a da linha a tensão é a soma fasorial de e , portanto:
Do terminal a podemos retirar ainda a relação:
Considerando o terminal a como o ponto onde z = 0:
como em z= 0,
podemos escrever:
fazendo algumas manipulações algébricas:
À relação chamamos de coeficiente de reflexão e representamos pela letra grega Γ
Para diferenciar o coeficiente de reflexão na carga do obtido em outro ponto da linha iremos identificar esse por
coeficiente de reflexão afastado da carga
O valor de Γ em qualquer ponto da linha será dado pela relação entre , sendo assim para um ponto afastado uma distância da carga teremos:
considerando um deslocamento a partir da carga (z=0) para a esquerda (sentido -z) temos:
Impedância de entrada
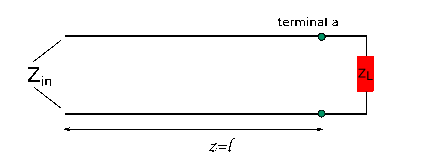
A relação entre a tensão e a corrente total em um determinado ponto da linha de transmissão é conhecida como Zin, impedância de entrada.
figura 3: Impedância de entrada - é a impedância vista em um ponto da linha.
Observe que é dada em função de
não estamos nos referindo a Zo (impedância característica) esta corresponde a relação , enquanto que Zin é dada por:
substituindo e por:
temos:
agora substituindo :
dividindo numerador e denominador por e lembrando que:
temos:
Potência incidente, entregue à carga e refletida
Potência incidente
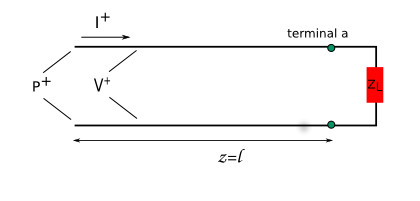
Ao conectar uma fonte em uma linha de transmissão, passa a se propagar pela linha uma onda de tensão e outra de corrente. Essas duas ondas transportam energia elétrica (figura 1).
Figura 4: linha percorrida por onda de tensão e corrente que transmitem potência elétrica.
Se a fonte de tensão for harmônica, cossenoidal por exemplo, podemos calcular a potência média ativa transmitida por:
- (3)
- e são dados por:
- (4)
- (5)
O termo na equação (5) corresponde ao ângulo de defasagem entre a tensão e a corrente na linha.
Substituindo (4) e (5) em (3) e lembrando que :
o que pode ser escrito como:
| (7) |
A equação (7) representa a potência transmitida na linha ou potência incidente. Note que a constante α representa a constante de atenuação da linha.
Potência entregue à carga
A potência ativa entregue à carga pela linha () pode ser calculada por:
Que pode ser reescrita em função das tensões e correntes no terminal a da linha de transmissão.
Considerando o terminal a como o ponto onde z=0:
o termo é exatamente a potência incidente no terminal a portanto:
| (8) |
A linha em na equação (8) representa que o cálculo de deve ser realizado descontando a atenuação da linha, isto é utilizando o valor de no terminal a.
Potência Refletida
Manipulando um pouco a equação (8) podemos encontrar o relação entre a potência incidente, a potência refletida e a potência entregue à carga:
| (9) |
O primeiro termo do lado direito da equação (9) corresponde a potência incidente no terminal a e o segundo termo a potência refletida no mesmo terminal. Esta relação mostra que a parcela de potência que chega ao final da linha e não é absorvida pela carga, retorno para linha. Isto é, e são as ondas refletidas na linha e transportam a potência refletida.
Potências na linha e entregue à carga
| Potência incidente | |
| Potência refletida | |
| Potência entregue à carga |