CEL18702 AULA04

1 Análise de Circuitos Elétricos de CC em Regime Permanente

1.1 Leis de Kirchhoff

Inicialmente, será apresentada uma discussão sobre polaridade e tensão nos elementos componentes de um circuito elétrico. Desta forma, será possível calcular a tensão nos extremos do trecho de um circuito. Para geradores e receptores ideais, independentemente do sentido da corrente elétrica, o traço menor representa o polo negativo e o traço maior corresponde ao polo positivo, conforme a Figura 1.

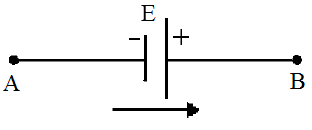
Figura 1 - Representação da polaridade de um gerador ou um receptor ideal.

O polo B tem potencial elétrico maior que o polo A, ou seja, no sentido da seta da Figura 1, a tensão é positiva. Logo, tem-se:

$V_B-V_A=+E$

$V_A-V_B=-E$

Para os resistores, a polaridade é dada pelo sentido da corrente: o polo positivo é o da entrada da corrente, e negativo é o da saída, segundo a Figura 2.

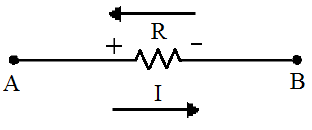
Figura 2 - Representação da polaridade da tensão em um resistor.

O polo A tem potencial elétrico maior que o polo B, ou seja, a tensão é positiva no sentido oposto ao de circulação da corrente. Logo, tem-se:

$V_A-V_B=+R.I$

$V_B-V_A=-R.I$

Portanto, para o cálculo da tensão entre os extremos de um trecho de circuito, deve-se:

• Verificar o sentido de circulação da corrente;
• Marcar as polaridades das tensões de acordo com tal sentido;
• Efetuar o somatório das mesmas.

Na Figura 3, tem-se um exemplo básico.

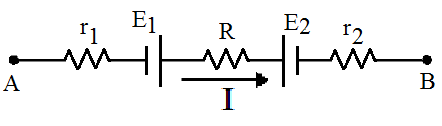
Figura 3 - Trecho do circuito.

Seguindo os passos anteriormente descritos, chega-se à Figura 4.

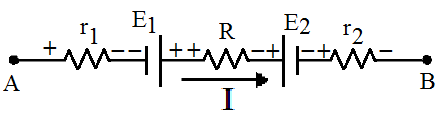
Figura 4 - Trecho do circuito com marcação das tensões.

Assim, a diferença potencial entre A e B é:

$V_A-V_B=+r_1.I-E_1+R.I+E_2+r_2.I$

1.2 Lei dos Nós

Em um circuito elétrico, denomina-se nó um ponto comum a três ou mais condutores. Veja Figura 5.

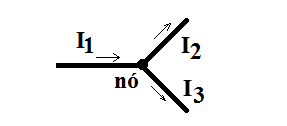
Figura 5 - Nó de um circuito.

Assim, pode-se enunciar a primeira lei de Kirchhoff: “A soma das intensidades das correntes que chegam a um nó é igual à soma da intensidade das correntes que saem do mesmo”. No exemplo da Figura 5, tem-se:

$I_1=I_2+I_3$

1.3 Lei das Malhas

Em um circuito elétrico, denomina-se malha um conjunto de elementos de circuito constituindo um percurso fechado, como é mostrado na Figura 6.

Figura 6 - Malha de um circuito.

Assim, pode-se enunciar a segunda lei de Kirchhoff: “Percorrendo uma malha em um certo sentido, partindo e chegando ao mesmo ponto, a soma algébrica das tensões é nula”. No exemplo da Figura 6, tem-se a malha ABCD. Partindo-se do ponto A, adotando-se o sentido horário e retornando ao mesmo ponto, pode-se escrever:

$R_2.I_2+E_2+r_2.I_2+R_1.I_2+r_1.I_1-E_1=0$

2 Aplicação da Lei de Kirchoff com Fontes Dependentes

Tomemos como exemplo o circuito abaixo e façamos uma análise do mesmo utilizando a lei da soma de tensões. Vamos determinar a corrente sobre os elementos, a tensão Vx e a potência fornecida e absorvida pelos elementos do circuito.

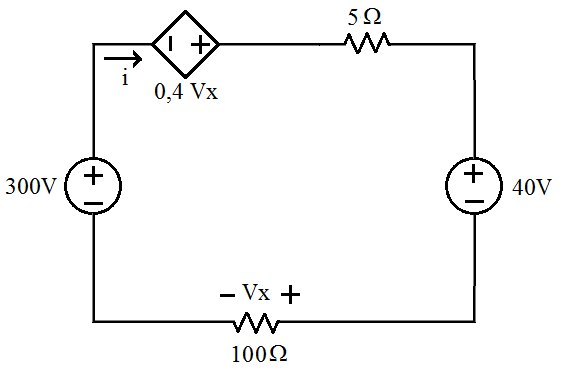
Aplicando a lei das tensões

$-300-0,4V_x+5i+40+V_x=0$

Resolvendo o sistema

$-260-40i+5i+100i=0$

$i=\frac{260}{65}=4A$

Logo

$V_x=400V$

A potência fornecida pela fonte de 300V

$P_{f300}=300.4=1200W$

A fonte 0,4Vx está fornecendo potência

$P_{f0,4Vx}=0,4V_{x}i=0,4.400.4=640W$

A potência absorvida pelo resistor de 5$\mathrm{\Omega }$ é

$P_{a5\mathrm{\Omega }}=5.i^2=5.16=80W$

A fonte de 40V está absorvendo potência

$P_{40V}=40.4=160W$

A potência absorvida pelo resistor de 100$\mathrm{\Omega }$ é

$P_{a100\mathrm{\Omega }}=100.i^2=100.16=1600W$

Devemos agora verificar se a soma das potências fornecidas é igual a soma das potências absorvidas para comprovação do princípio de conservação de energia.

$\sum _{}^{}{P}_f=1200+640=1840W$

$\sum _{}^{}{P}_a=80+160+1600=1840W$

Com isto fizemos uma análise completa do comportamento de cada um dos elementos do circuito e comprovamos que a potência fornecida é igual à potência consumida.

3 Exercício de Fixação

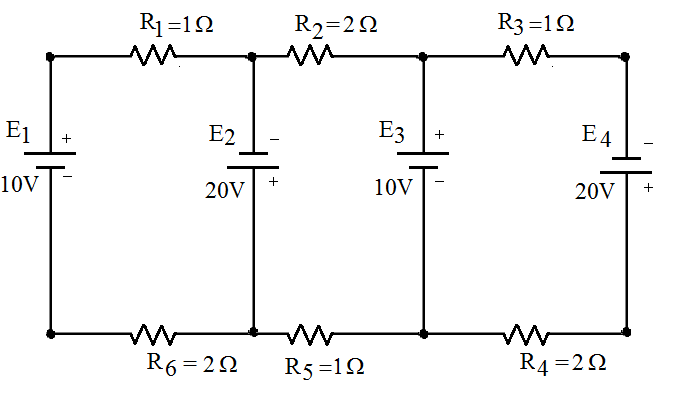
Solução

A primeira coisa a se fazer é atribuirmos um sentido de corrente. Depois, atribuir um sentido para cada malha, que também pode ser aleatório. No caso do circuito acima, preferimos utilizar o sentido horário. Aplicando o lei do nós $i_1=i_2+i_6(I)$ $i_2=i_3+i_4(II)$ $i_5=i_3+i_4(III)$ Malha A $-10+1.i_1-20+2i_1=03i_1=30i_1=\frac{30}{3}{i}_1=10A$ Malha B $+20+2.i_2+10+1i_5=02i_2+1i_5=-30$ Malha C $-10+1.i_3-20+2i_3=03i_3=30i_3=\frac{30}{3}{i}_3=10A$ Substituindo os valores de $i_{1}e{i}_3$em I, II e III: $i_1=i_2+i_{6}10=i_2+i_6{i}_2+i_6=10$ $i_2=i_3+i_4{i}_2=10+i_4{i}_2-i_4=10$ $i_5=i_3+i_4{i}_5=10+i_4{i}_5-i_4=10$ Mais IV, forma-se um sistema de quatro equações e quatro incógnitas. $i_2+i_6=10$ $i_2-i_4=10$ $i_5-i_4=10$ $2i_2+i_5=-30$ Isolando... $i_4=i_2-10$ Substituindo... $i_5-(i_2-10)=10i_5-i_2+10=10i_5-i_2=0i_5=i_2$ $2i_2+i_2=-303i_2=-30i_2=-\frac{30}{3}{i}_2=-10A$ Assim... $i_5=i_2{i}_5=-10A$ $i_4=i_2-10i_4=-10-10i_4=-10A$ Por último... $i_2+i_6=10-10+i_6=10i_6=10+10i_6=20A$ Como o valor das correntes $i_2,i_{4}e{i}_5$ são negativos, isto significa que foram atribuídos sentidos contrários no exercício.

4 Referências

[1] http://www.infoescola.com/eletricidade/leis-de-kirchhoff/

[2] https://pt.wikipedia.org/wiki/Leis_de_Kirchhoff

[3] http://www.feng.pucrs.br/~virgilio/Circuitos_Eletricos_I/Capitulo2_ckt1.pdf

---

<<	<>	>>