CEL18702 2017 2 AULA04

1 Análise de Nodal

Conforme visto anteriormente, a solução de um circuito elétrico contendo N malhas requer a determinação de N incógnitas, as quais são as correntes imaginárias de cada uma das malhas. Também foi mostrado que a aplicação das Leis de Kirchoff e a consideração das relações tensão e corrente de cada nó ou malha permite estabelecer as equações necessárias para a solução do circuito. No entanto, a solução fica mais simples quando se utiliza um conjunto de variáveis distinto das variáveis de nó. No caso da análise de nós serão utilizadas as tensões dos nós do circuito em relação a um nó de referência, ao invés da tensão de malha (tensão entre os terminais de cada ramo). Desta forma será obtido um sistema de equações tendo como incógnitas as tensões dos nós do circuito em relação ao nó de referência, o qual pode ser escolhido como qualquer nó do circuito. A aplicação sistemática deste procedimento é denominada Análise Nodal e é descrita resumidamente a seguir

2 Parte I

Análise de circuitos mais gerais acarreta na solução de um conjunto de equações. Análise nodal:

• Tensões são as incógnitas a serem determinadas.
• Deve-se escolher um nó do circuito como referência.
• Associar aos outros nós uma tensão em relação ao nó de referência (tensão de nó).
• Polaridade de um nó é escolhida de tal forma que as tensões dos nós sejam positivas em relação ao nó de referência.
• Nó de referência é geralmente escolhido como o que possui o maior número de ramos conectados.
• Nó de referência possui potencial zero (terra).
• Aplica-se então a lei de Kirchhoff para corrente nos nós.
• As correntes nos elementos são proporcionais às tensões sobre os mesmos.

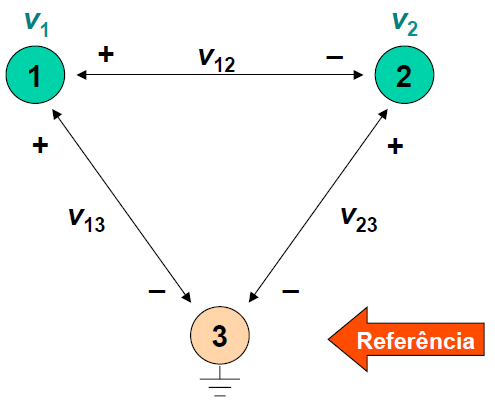
Figura 1 - Tensões de Nó: $V_1$ e $V_2$.

$V_{12}=V_1-V_2$

$V_{13}=V_1-0=V_1$

$V_{23}=V_2-0=V_2$

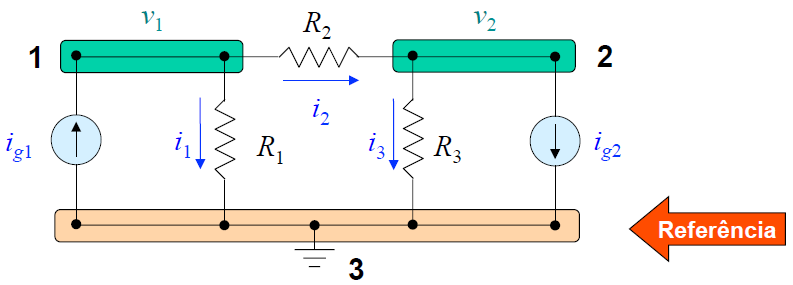
Figura 2 - Circuitos com dois Nós.

Lei de Kirchhoff de correntes

Nó 1: $i_1+i_2-i_{g1}=0$ ou em termos de tensões: $\frac{V_1}{R_1}+\frac{(V_1-V_2)}{R_2}-i_{g1}=0$

Nó 2: $-i_2+i_3+i_{g2}=0$ ou em termos de tensões: $\frac{(V_2-V_1)}{R_2}+\frac{V_2}{R_3}+i_{g2}=0$

2.1 Exercício de Fixação

Utilizando a análise nodal, determine as tensões sobre os resistores no circuito abaixo:

[a] Determine os nós do circuito.

[b] Aplique a lei de Kirchoff para os nós indicados.

[c] Equacionar o circuito lembrando que é a soma de corrente e não de tensões como acontece nas malhas.

[d] Solucione utilizando substituição, regra de CRAMER (matrizes) ou escalonamento.

Solução

Nó 1 (V1) $-5+\frac{V_1}{2}+\frac{V_1}{5}+\frac{V_1-V_2}{2}=0$ $\frac{V_1}{2}+\frac{V_1}{5}+\frac{V_1}{2}-\frac{V_2}{2}=5$ mmc $\frac{5V_1+2V_1+5V_1-5V_2}{10}=5$ passa multiplicando o 10 $12V_1-5V_2=5.10$ $12V_1-5V_2=50$ Nó 2 (V2) $-3+\frac{V_2}{4}+\frac{V_2-V_1}{2}=0$ $\frac{V_2}{4}+\frac{V_2}{2}-\frac{V_1}{2}=3$ mmc $\frac{V_2+2V_2-2V_1}{4}=3$ $-2V_1+3V_2=3.4$ $-2V_1+3V_2=12$ Resolvendo o sistema (Cramer) $\mathrm{\Delta }=\left|\begin{array}{cc}12& -5\\ -2& 3\end{array}\right|.\left|\begin{array}{c}50\\ 12\end{array}\right|$ $\mathrm{\Delta }=\left|\begin{array}{cc}12& -5\\ -2& 3\end{array}\right|=36-10\mathrm{\Delta }=26$ $\mathrm{\Delta }{V}_1=\left|\begin{array}{cc}50& -5\\ 12& 3\end{array}\right|=150-(-60)\mathrm{\Delta }{V}_1=210$ $\mathrm{\Delta }{V}_2=\left|\begin{array}{cc}12& 50\\ -2& 12\end{array}\right|=144-(-100)\mathrm{\Delta }{V}_2=244$ $V_1=\frac{\mathrm{\Delta }{V}_1}{\mathrm{\Delta }}=\frac{210}{26}{V}_1=8,07V$ $V_2=\frac{\mathrm{\Delta }{V}_2}{\mathrm{\Delta }}=\frac{244}{26}{V}_2=9,38V$

2.2 Exercícios

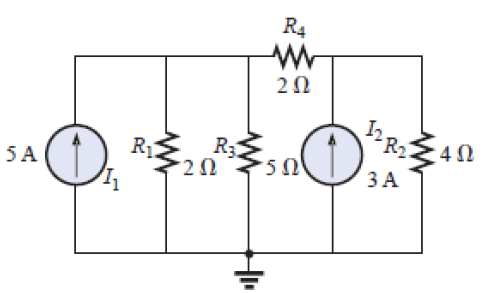
[a] Usando análise nodal, determine as tensões sobre os resistores indicados:

Resultado
Resultado: V1=4,8V; V2=6,4V

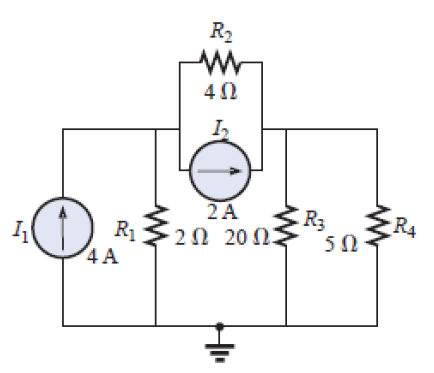
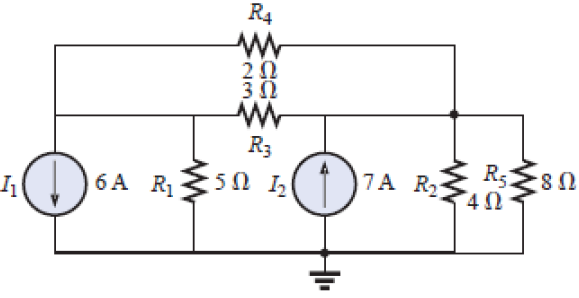
[b] Usando análise nodal, determine as tensões sobre os resistores indicados:

Resultado
Resultado: V1=-2,55V; V2=4,03V;

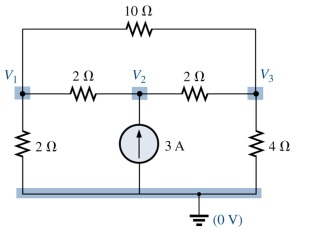
[c] Usando análise nodal, determine as tensões sobre todos os nós:

Resultado
Resultado: V1= 3,7V; V2= 7,2V; V3= 4,6V;

3 Parte II

Anteriormente, estudamos circuitos resistivos utilizando análise nodal. Agora vamos transformar as resistências em condutâncias e resolver esses mesmos circuitos da mesma forma de como se fossem resistências, retirando a questão das frações das equações.

Nota: Um circuito com três nós terá duas tensões incógnitas e duas equações; um circuito com dez nós terá nove tensões desconhecidas e nove equações; um circuito com N nós terá N-1 tensões incógnitas e N-1 equações.

3.1 Condutância

Vamos abrir um parênteses para falar sobre condutância. A ideia é que os circuitos fiquem em "termos" de multiplicação e não de divisão. A Figura 1 mostra um exemplo que permite escrever as equações de nós por inspeção direta em função da tensão dos nós.

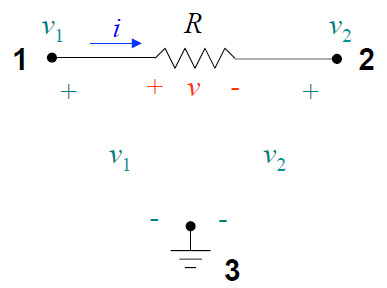
Figura 1 - Exemplos de circuito resistivo x condutivo.

$V=V_1-V_2$

$i=\frac{V}{R}=\frac{V_1-V_2}{R}$ ou $i=\frac{V}{R}=G(V_1-V_2)$

Fórmula matemática da condutância

Para calcular a condutância de um determinado condutor, temos que saber o valor da sua resistência. Assim, e sabendo que a condutância é o inverso da resistência, chegamos à seguinte fórmula:

$G=\frac{1}{R}$

Se tivermos por exemplo, um condutor em que a resistência seja igual a 10Ω, substituímos o R de resistência por 10Ω e obtemos o seguinte cálculo:

Então

$G=\frac{1}{R}=\frac{1}{10}=0,1S(siemens)$

Logo com este cálculo concluímos que um condutor com uma resistência de 10Ω, tem uma condutância de 0,1 siemens.

3.2 Exemplo 1

Tomemos esse exemplo para o qual faremos a mesma análise do dos exercícios anteriores. O exemplo que se segue é de um circuito com um único par de nós possuindo também fontes dependentes:

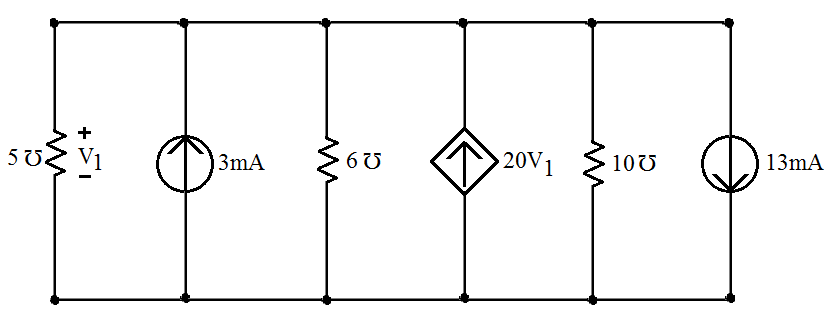
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes.

Como se pode verificar, a tensão $V_1$ aplicada sobre a condutância de 5 está também aplicada sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a seta dirigida para o nó inferior e aplicamos a lei dos nós.

$5V_1-0,003+6V_1-20V_1+10V_1+0,013=0$

$1V_1=-0,003-0,013\to V_1=-0,01V$

Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida ou consumida por cada um dos elementos.

Na condutância 5

$i_5=5V_1=-0,05A$

$P_5=5V_1^2=5(-0,01{)}^2=5.10^{-4}W$

Na condutância 6

$i_6=6V_1=-0,06A$

$P_6=6V_1^2=5(-0,01{)}^2=6.10^{-4}W$

Na condutância 10

$i_{10}=10V_1=-0,1A$

$P_{10}=10V_1^2=10(-0,01{)}^2=1.10^{-3}W$

Potência fornecida pela fonte de 3mA

$P_{f3ma}=0,003V_1=-0,3.10^{-4}W;P_a=0,3.10^{-4}W$

Potência fornecida pela fonte de 13mA

$P_{f13ma}=-0,013V_1=-1,3.10^{-4}W$

Potência fornecida pela fonte dependente

$P_{f20Vx}=20V_1.V_1=20V_1^2=20(-0,01{)}^2=20.10^{-4}W$

Por último, fazemos o balanço das potências

$\sum _{}^{}{P}_f=1,3.10^{-4}+20.10^{-4}=21,3.10^{-4}W$

$\sum _{}^{}{P}_a=5.10^{-4}+6.10^{-4}+0,3.10^{-4}=21,3.10^{-4}W$

3.3 Exemplo 2

Utilizando análise nodal encontre as tensões nos nós do circuito e encontre as correntes em todos os resistores.

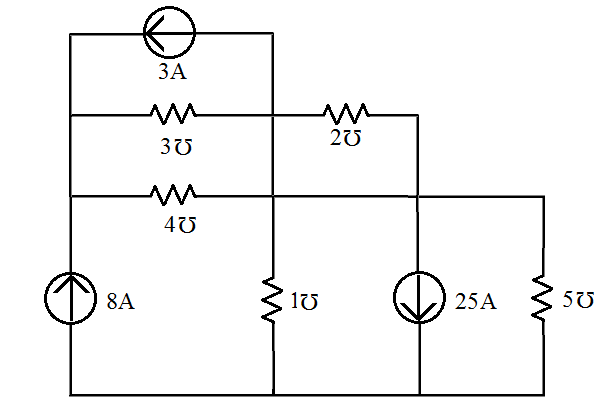
Resolvendo o Circuito

Definindo os nós do circuito ($V_{1}e{V}_2$).

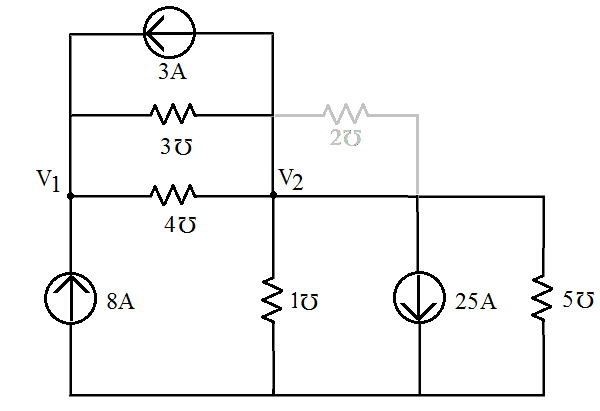
Percebe-se que a condutância de 2 está curtocircuitada, portanto, não será considerada no sistema.

Outra definição importante é que devemos atribuir o sinal da corrente que chega e que sai do nó. Podendo ser negativas as correntes que chegam no nó e positivas as correntes que saem do nó. Lembrando, não há nenhum problema em arbitrar essas corrente de forma contrária, tendo como resultados os valores com troca de sinal.

Resposta
V1=-1,26V; V2=-2,83V;

4 Exercícios

[1] Ache as tensões dos nós $V_{1}e{V}_2$

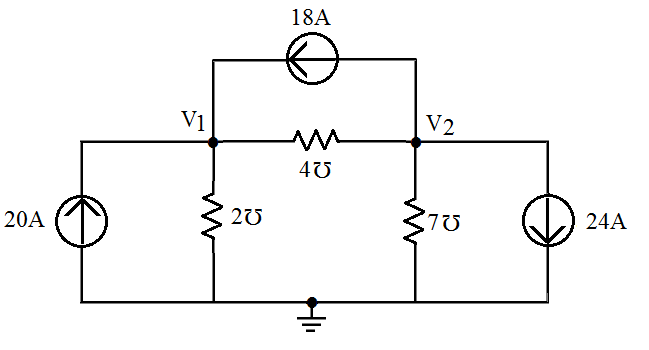
Solução
Nó 1 $(2+4)v_1-4v_2=20+18$ $6v_1-4v_2=38$ Nó 2 $(4+7)v_2-4v_1=-18-24$ $-4v_1+11v_2=-42$ Resultado $V_1=5V$ $V_2=-2V$

[2] Ache as tensões dos nós $V_1,V_{2}e{V}_3$

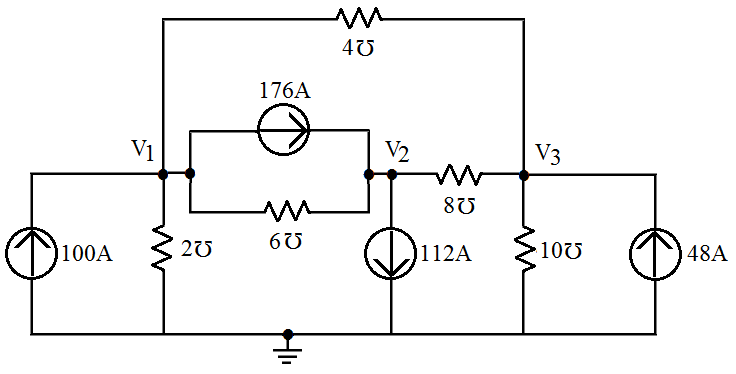
Solução
Resultado $V_1=-2V$ $V_2=4V$ $V_2=6V$

[3] Utilizando o método dos nós calcular a corrente I₀ para o circuito abaixo.

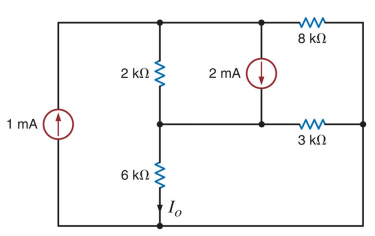
Respostas
I0=0,33uA

[4] Utilizando análise de nós, determine o valor de V_X para o circuito abaixo.

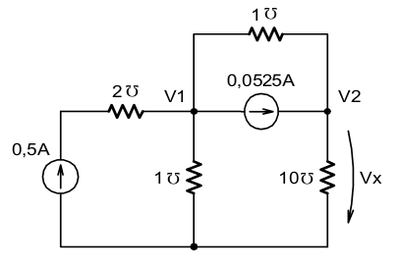
Respostas
VX=26,3mV

5 Referências

[1] http://www.feng.pucrs.br/~fdosreis/ftp/elobasicem/Aulas%202006%20II/AnaliseNodal.pdf

[2] http://www.decom.fee.unicamp.br/~baldini/EA513/Cap4.pdf

---