CEL18702 2016 2 AULA08

1 Condutância

Vamos abrir um parênteses para falar sobre condutância. A ideia é que os circuitos fiquem em "termos" de multiplicação e não de divisão. A Figura 3 mostra um exemplo que permite escrever as equações de nós por inspeção direta em função da tensão dos nós.

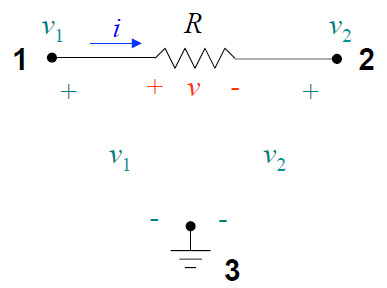
Figura 3 - Exemplos de circuito resistivo x condutivo.

$V=V_1-V_2$

$i=\frac{V}{R}=\frac{V_1-V_2}{R}$ ou $i=\frac{V}{R}=G(V_1-V_2)$

Fórmula matemática da condutância

Para calcular a condutância de um determinado condutor, temos que saber o valor da sua resistência. Assim, e sabendo que a condutância é o inverso da resistência, chegamos à seguinte fórmula:

$G=\frac{1}{R}$

Se tivermos por exemplo, um condutor em que a resistência seja igual a 10Ω, substituímos o R de resistência por 10Ω e obtemos o seguinte cálculo:

Então

$G=\frac{1}{R}=\frac{1}{10}=0,1S(siemens)$

Logo com este cálculo concluímos que um condutor com uma resistência de 10Ω, tem uma condutância de 0,1 siemens.

2 Análise com dois nós

Tomemos um novo exemplo para o qual faremos a mesma análise do exemplo anterior. O exemplo que se segue é de um circuito com um único par de nós possuindo também fontes dependentes:

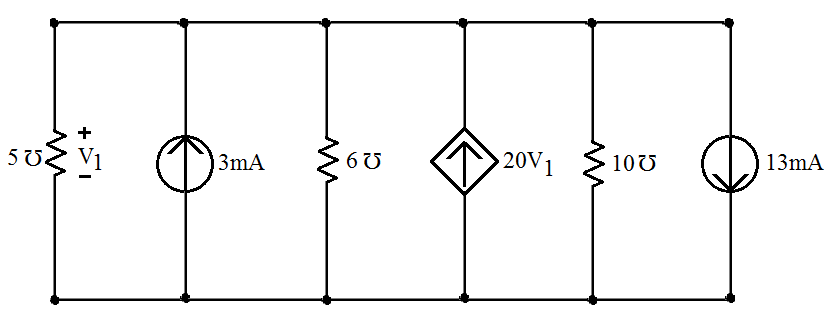
Figura 1 - Aplicação da lei dos nós a um circuito com fontes dependentes.

Como se pode verificar, a tensão $V_1$ aplicada sobre a condutância de 5 está também aplicada sobre todos os elementos do circuito. Considerando que a corrente sobre as condutâncias estão com a seta dirigida para o nó inferior e aplicamos a lei dos nós.

$5V_1-0,003+6V_1-20V_1+10V_1+0,013=0$

$1V_1=-0,003-0,013\to V_1=-0,01V$

Podemos agora determinar as correntes sobre as condutâncias assim como a potência fornecida ou consumida por cada um dos elementos.

Na condutância 5

$i_5=5V_1=-0,05A$

$P_5=5V_1^2=5(-0,01{)}^2=5.10^{-4}W$

Na condutância 6

$i_6=6V_1=-0,06A$

$P_6=6V_1^2=5(-0,01{)}^2=6.10^{-4}W$

Na condutância 10

$i_{10}=10V_1=-0,1A$

$P_{10}=10V_1^2=10(-0,01{)}^2=1.10^{-3}W$

Potência fornecida pela fonte de 3mA

$P_{f3ma}=0,003V_1=-0,3.10^{-4}W;P_a=0,3.10^{-4}W$

Potência fornecida pela fonte de 13mA

$P_{f13ma}=-0,013V_1=-1,3.10^{-4}W$

Potência fornecida pela fonte dependente

$P_{f20Vx}=20V_1.V_1=20V_1^2=20(-0,01{)}^2=20.10^{-4}W$

Por último, fazemos o balanço das potências

$\sum _{}^{}{P}_f=1,3.10^{-4}+20.10^{-4}=21,3.10^{-4}W$

$\sum _{}^{}{P}_a=5.10^{-4}+6.10^{-4}+0,3.10^{-4}=21,3.10^{-4}W$

3 Exercícios

[1] ...

Solução
...

[2] ...

Solução
...