CEL18702 2017 1 AULA19

1 Sistemas Trifásicos

1.1 Características dos Sistemas Trifásicos

• Um sistema trifásico (3ø) é uma combinação de três sistemas monofásicos (1ø) defasados de 120° um dos outros.
• Os circuitos trifásicos exigem peso menor dos condutores do que os circuitos monofásicos de mesma especificação de potência.

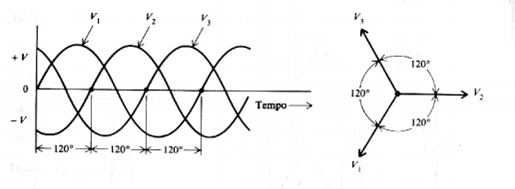
Figura 1 - a) Triângulo de potência com S-Q-P e b) Três fasores de tensão correspondentes.

1.2 Ligação em estrela ou triângulo

• As 3 (três) fases de um sistema trifásico podem ser ligadas de duas formas:

a) Ligação em estrela (Y), ou

b) Ligação em triângula (Δ).

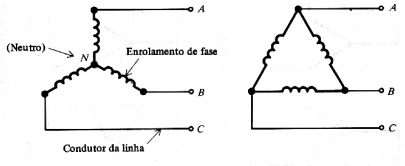
Figura 2 - a) Liagação em Y ou estrela e b) Ligação em triângulo ou Δ.

• Na ligação Y o quarto condutor do sistema a quatro fios é o ponto neutro N.

1.3 Nomenclaturas

V_l é a tensão de linha (tensão entre fases);

V_f é a tensão de fase (tensão entre fase e neutro);

I_l é a corrente de linha;

I_f é a corrente de fase;

$a=\frac{N_1}{N_2}$ é a razaõ entre o número de espiras.

2 Potência em cargas trifásicas equilibradas

Uma carga equilibrada tem a mesma impedância em cada enrolamento do secundário. A Figura 3 mostra como exemplo o Motor Elétrico.

Figura 3 - Exemplo: Motor Elétrico.

2.1 Carga Delta (Δ) equilibrada

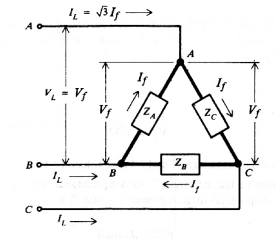
Figura 4 - Carga Δ equilibrada, Z_A=Z_B=Z_C=Z_Δ.

$V_f=V_l$

$I_f=\frac{I_l}{\sqrt{3}}$

2.2 Carga Estrela (Y) equilibrada

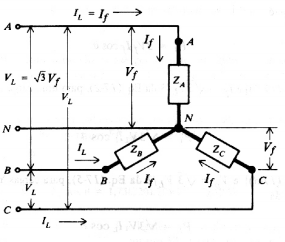
Figura 5 - Carga Y equilibrada, Z_A=Z_B=Z_C=Z_Y.

$I_f=I_l$

$V_f=\frac{V_l}{\sqrt{3}}$

2.3 Potência trifásica total

A potência trifásica é definida como sendo 3 (três) vezes a potência monofásica. Logo:

$P_{3\varphi }=3.P_{1\varphi }$

$P_{1\varphi }=V_f.I_f.cos(\theta )$

2.4 Relação das potências trifásicas

A Figura 6 mostra o triângulo de potência.

Figura 6 - Relação do triângulo de potência para um circuito 3-ø

Logo

$P_T=\sqrt{3}.V_l.I_l.cos(\theta )$

$S_T=\sqrt{3}.V_l.I_l$

$Q_T=\sqrt{3}.V_l.I_l.sin(\theta )$

Onde

P_T é a potência total ativa (real) em [W];

S_T é a potência total aparente em [VA];

Q_T é a potência total reativa em [VAr];

θ é o ângulo de fase de carga.

2.5 Exemplo

Três resistências de 20 ohms cada estão ligadas em Y a uma linha 3ø de 240V funcionando a um FP de uma unidade.

Calcule

a) Corrente através de cada resistência;

b) Corrente de linha;

c) Potência consumida pelas três resistências.

Solução
a) Resposta $V_l=\sqrt{3}.V_f$ $V_f=\frac{V_l}{\sqrt{3}}=\frac{240}{1,73}=138,7V$ $I_f=\frac{V_f}{Z_f}=\frac{V_f}{R_f}=\frac{138,7}{20}=6,94A$ b) Resposta $I_l=I_f=6,94A$ c) Resposta $P_T=3.P_f=3.V_f.I_f.cos(\theta )=3.138,7.6,94.1=2890W$

2.6 Exercício

[1] Repita o Exemplo acima para o caso em que as três resistências são religadas em triângulo.

Resposta
a) If=12A; Il=20,8A; PT=8640W

[2] Um sistema 3ø de três fios tem uma corrente de linha de 25A e uma tensão de linha de 1000V. O fator de potência da carga é 86,6 por cento indutivo. Calcule:

a) a potência real liberada;

b) a potência reativa;

c) a potência aparente;

d) desenhe o triângulo de potência.

Resposta
a) PT=37,5W; b) QT=21,6kVAr; c) ST=43,3kW; d) desenho do triangulo com 30°

3 Cargas trifásicas não equilibradas

Quando as impedâncias das três cargas não forem iguais entre si, o fasor resultante da soma das correntes será diferente de zero e a corrente de Neutro (I_N) não será nula. A Figura 7 traz um exemplo de Quadro Geral de Distribuição.

Figura 7 - Quadro Geral de Distribuição.

4 Referência Bibliográfica

GUSSOW, Milton. Eletricidade Básica, 2ª Edição, Revisada e Ampliada.

---