FundamentacaoTeoricaProjeto-CoordenadasEsfericasAzimute

1 Objetivos

O aluno deverá ser capaz de:

• Usar as coordenadas geográficas entre dois pontos para cálculo da distância geodésica entre dois pontos usando o Scratch;
• Calcular o azimute usando o Scratch.

2 Coordenadas Esféricas

Material de referência:

Monografia de Luciana Cadar Chamone

Slides de Luciana Cadar Chamone

3 Implementação no Scratch

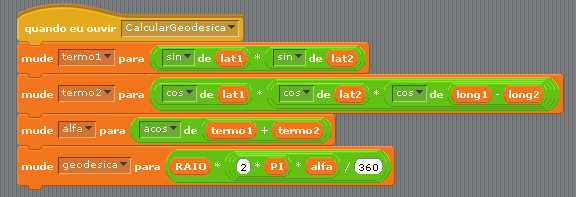
3.1 Cálculo da distância geodésica

Exercício 1: Elaborar um subprograma no Scratch que recebe como parâmetros dois pontos (LAT1,LONG1) e (LAT2,LONG2) em graus e a função retorna a distância geodésica em Km e o ângulo $\alpha$ relativo a esta geodésica (usar $Rt=6.366Km$ - raio da terra).

SUGESTÃO: Aplicar direto:

$Sg=R{\cos }^{-1}[\sin ({\varphi }_1)\sin ({\varphi }_2)+\cos ({\varphi }_1)\cos ({\varphi }_2)\cos ({\lambda }_1-{\lambda }_2)]$

pois esta fórmula é diretamenteamente derivada da lei dos cosenos, sendo:

$({\varphi }_1,{\lambda }_1)$ e $({\varphi }_2,{\lambda }_2)$ as coordenadas geográficas dos pontos.

OBS: O ângulo $\alpha$  facilitará o cálculo dos azimutes entre os pontos.

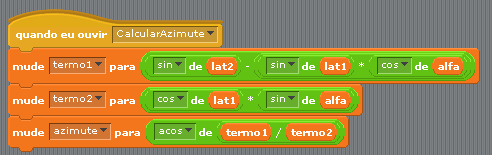
3.2 Cálculo da distância geodésica

Exercício 2: Elaborar um programa Scratch que recebe as coordenadas de dois pontos A e B e calcula o azimute do ponto A ($({\varphi }_1,{\lambda }_1)$) em relação ao ponto B ($({\varphi }_2,{\lambda }_2)$).

SUGESTÃO: Aplicando as leis do cosenos pode-se aplicar a seguinte fórmula: $Az=({\cos }^{-1}[(\sin ({\varphi }_2)-\sin ({\varphi }_1)\cos (\alpha ))/(\cos ({\varphi }_1)\sin (\alpha ))]$

Solução para os problemas acima:

3.3 Cálculo da Atenuação da Potência

A seguinte fórmula pode ser usada para cálculo da atenuação de potência:

$P_r=P_t{\left(\frac{\lambda }{4\pi d}\right)}^2$

onde $P_t$ e $P_r$ são as potências transmitidas e recebidas, $\lambda$ o comprimento de onda e $d$ a distância entre os pontos. Considere que os ganhos das antenas são unitários.

Exercício: elabore um programa scratch para, dado as potências transmitidas, distância e comprimento de onda, calcular a potência recebida.

3.4 Cáclulo do ângulo de Alinhamento de Altura entre as antenas

Baseando-se em Pitágoras calcule o ângulo para alinhamento entre dois pontos com coordenadas e alturas conhecidas. Faça um programa scratch para calcular este ângulo.