CEL18702 2017 1 AULA04: mudanças entre as edições
| Linha 185: | Linha 185: | ||
;Sabe-se: | ;Sabe-se: | ||
<math>i_3=6A</math> | <math>i_3=6A\,</math> | ||
;malha 1 | ;malha 1 | ||
<math>-6+2(i_1-i_2)+1(i_1-i_3)=0 </math> | <math>-6+2(i_1-i_2)+1(i_1-i_3)=0\, </math> | ||
<math>-6+2i_1-2i_2+1_1-6=0 </math> | <math>-6+2i_1-2i_2+1_1-6=0\,</math> | ||
<math>3i_1-2i_2=12</math> | <math>3i_1-2i_2=12\,</math> | ||
;malha 2 | ;malha 2 | ||
<math>4i_2+3(i_2-i_3)+2(i_2-i_1)=0 </math> | <math>4i_2+3(i_2-i_3)+2(i_2-i_1)=0\,</math> | ||
<math>4i_2+3i_2-18+2i_2-2i_1=0</math> | <math>4i_2+3i_2-18+2i_2-2i_1=0\,</math> | ||
<math>-2i_1+9_i2=18</math> | <math>-2i_1+9_i2=18\,</math> | ||
Edição das 19h49min de 1 de março de 2017
1 Análise de Malhas
A Análise de Malhas é uma técnica utilizada em análise de circuitos baseada na simplificação do circuito do ponto de vista da "soma" de tensões. O método de análise das malhas só é aplicado às redes planares, isto é, somente se for possível desenhar o diagrama de um circuito numa superfície plana, sem que haja cruzamento dos ramos, então o circuito é dito planar. Na Figura 1 temos um exemplo de rede planar e não planar.
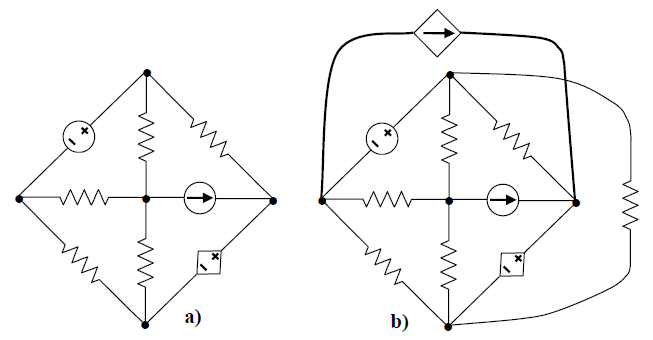
Figura 1 - Rede planar (a) e Rede não planar (b).
Um circuito é uma rede que contém pelo menos um caminho fechado por onde possa fluir corrente. O nome oficial para esse caminho é laço. Assim, se iniciarmos por um determinado nó e traçarmos pela rede uma linha fechada contínua, passando uma vez em cada nó e terminando no nó de partida, este caminho é um laço. A malha é uma propriedade de circuitos planares e é definida como sendo um laço que não contém nenhum outro por dentro.
A técnica de análise de malhas envolve o conceito de corrente de malha que definiremos como sendo a corrente que flui apenas no perímetro de uma malha. Vamos utilizar o exemplo da Figura 2 para melhor entendimento do método.
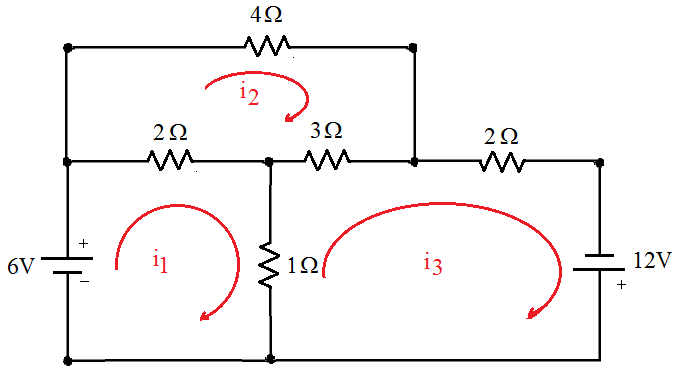
Figura 2 - Exemplo de aplicação do método de malhas.
- Solução
- Arbitramos as correntes de malhas dando a designação de para a malha 1, para a malha 2 e assim por diante;
- O sentido arbitrado para as correntes de malha pode ser qualquer um, mas para facilitar a obtenção das equações adotamos sempre o sentido horário;
- Escreve-se as equações de malha em termos das tensões utilizando a lei de Ohm
- Simplifica-se as equações e resolve-se o sistema obtido.
- Malha 1
- Malha 2
- Malha 3
Arrumando...
1.1 Exercício de Fixação
Determine o valor de todas as correntes no circuito e a queda de tensão nos resistores:
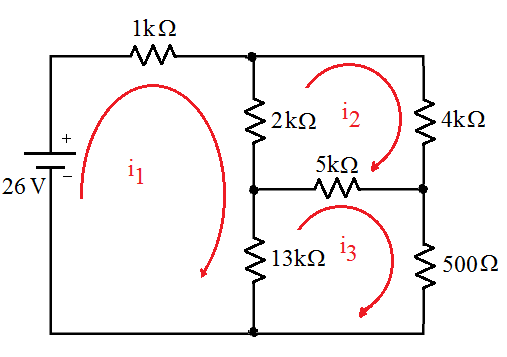
| Solução |
|---|
|
2 Exercícios AT1
[1] Determine a potência fornecida ou absorvida pelos elemento do circuito abaixo. (Kirchhoff)
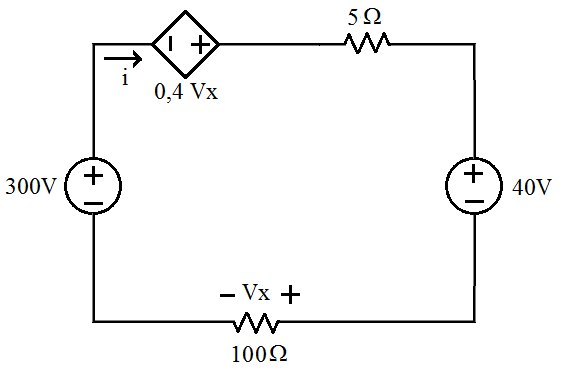
[2] Encontre as correntes para o circuito abaixo e a tensão sobre o resistor de 1 . (Malhas)
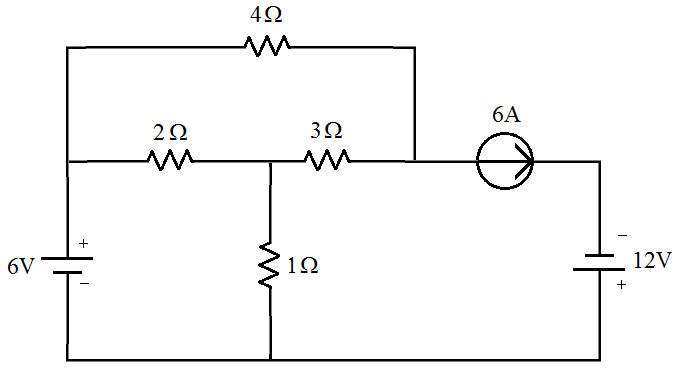
| Solução |
|---|
|
[3] Encontre a corrente para o circuito abaixo. (Malhas)
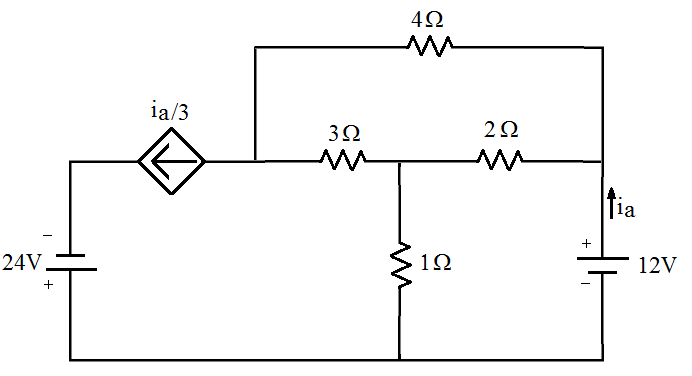
[4] Encontre as correntes para o circuito abaixo. (Malhas)
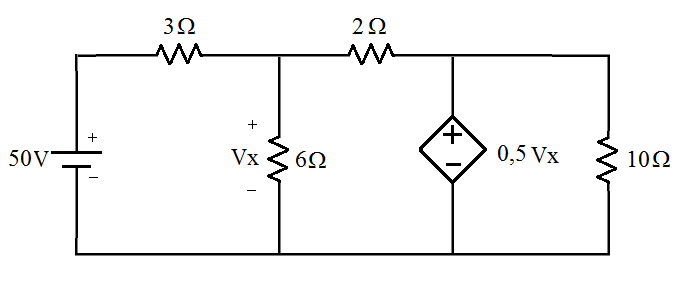
3 Referências