CEL18702 2016 2 AULA11

1 Objetivos

• Preparar-se para a AT2
• Exercitar Análise Nodal
• Exercitar Equivalentes de Thevenin e Norton

2 Lista de Exercícios

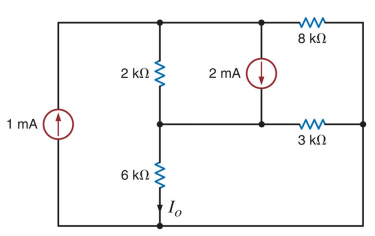
[1] Utilizando o método dos nós calcular a corrente I₀ para o circuito abaixo.

Respostas
I0=0,33mA

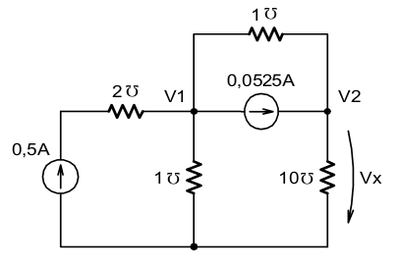
[2] Utilizando análise de nós, determine o valor de V_X para o circuito abaixo.

Respostas
VX=23,6mV

[3] Determine os equivalentes de Thévenin e de Norton do circuito abaixo. Calcule V_AB com R_c=3Ω ligada ao circuito.

Respostas
VTh=4,2V; RTh=RN=3Ω; IN=1,4A; VAB=2,1V

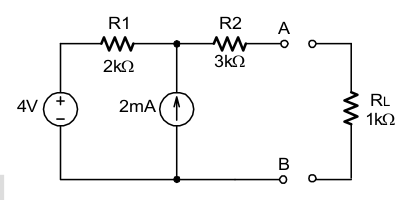
[4] Calcule os equivalentes de Thévenin e de Norton para o circuito abaixo. Calcule V_AB com R_L ligada ao circuito.

Solução

Pessoal! Descobri meu engano. Só existe uma malha de corrente no circuito e é a de 2mA. Lembre-se que entre A e B está aberto. Nosso equívoco foi tentar fazer duas malhas onde teríamos que aplicar a lei de Kirchoff das correntes. Vamos lá! Como não há corrente circulando pelo R2, a tensão VAB é a soma da queda de tensão no resistor R1 mais a fonte de 4V. Sabendo que a corrente de malha é 2mA fica: $V_{AB}=R_1.2.10^{-3}+4$ $V_{AB}=2.10^3.2.10^{-3}+4$ $V_{AB}=V_{Th}=8V$ Para calcular a resistência equivalente a fonte de corrente fica em aberto enquanto a fonte de tensão fica em curto, logo: $R_{eq}=2k+3k=5k\mathrm{\Omega }$ $R_{eq}=R_{Th}=5k\mathrm{\Omega }$ Para calcular o IN fazemos: $I_N=\frac{V_{Th}}{R_{Th}}=\frac{8}{5.10^3}=1,6mA$ VTh=8V; RTh=RN=5kΩ; IN=1,60mA; VAB=-1,33V

---

<<	<>	>>